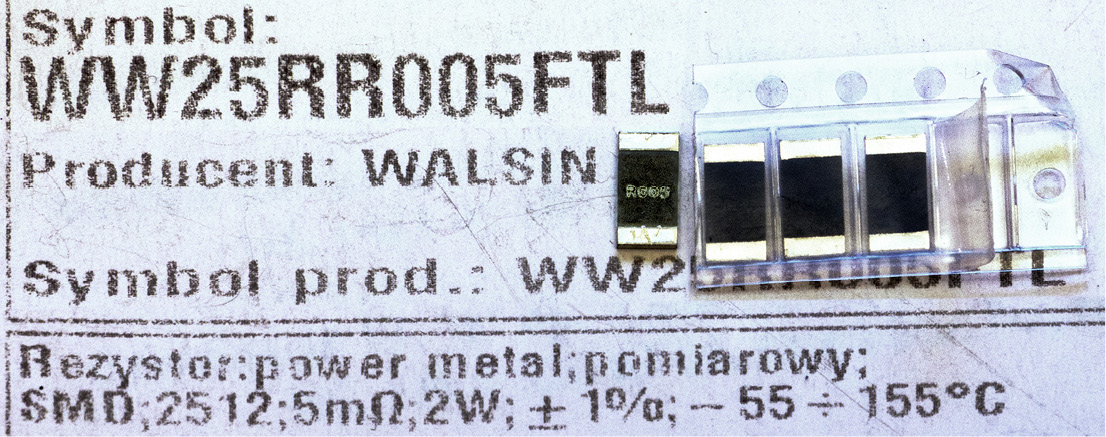Mikroomomierz

Artykuł pokazuje, w jak zaskakująco prosty sposób nawet w warunkach amatorskich można mierzyć znikomo małe rezystancje, poniżej 1 milioma czyli poniżej jednej tysięcznej oma, i to z rewelacyjną rozdzielczością 1 mikrooma, czyli milionowej części oma. Można mierzyć i warto mierzyć!

Głównym celem artykułu jest zachęcenie do pomiaru bardzo małych rezystancji, których obecność może mieć negatywny wpływ na działanie układów elektronicznych. Rezystancji rzędu miliomów, a nawet mikroomów, czyli takich, których pomiar za pomocą omomierza jest absolutnie niemożliwy.

Opisywana prosta przystawka pozwala zmierzyć bardzo małe rezystancje, nawet rzędu mikroomów. Tak, to nie pomyłka, teoretycznie nawet od 1 mikrooma! Nie tylko oporność rezystorów, ale też rezystancje przewodów, różnych połączeń i styków.

Problem pomiaru małych i bardzo małych oporności w ostatnich latach nabiera znaczenia, ponieważ coraz większą uwagę zwracamy na wszelkie straty i chcemy te straty minimalizować, co wiąże się między innymi właśnie ze stosowaniem i koniecznością pomiaru bardzo małych rezystancji.

Niniejszy artykuł jest też przykładem pokazującym, jak w praktyce wygląda projektowanie prostych układów elektronicznych.

Przykłady pomiaru maleńkich rezystancji

Fotografia tytułowa pokazuje pomiar rezystancji kawałka instalacyjnego kabla o przekroju 2,5 mm² i długości nieco ponad 1 cm za pomocą opisanej dalej przystawki. W ten sposób mierzymy rezystancję między punktami dołączenia sond woltomierza (między czerwonym i czarnym krokodylkiem), a nie mają znaczenia rezystancje pomocniczych przewodów połączeniowych. Jak widać, rezystancja tego kawałeczka dość grubego drutu wynosi 92 mikroomy (92 µΩ).

To bardzo dobrze zgadza się z teorią: rezystancja 1 centymetra miedzianego drutu o przekroju 2,5 mm² powinna wynosić około 70 mikroomów.

Fotografia A pokazuje pomiar rezystora SMD o znikomej rezystancji pięciu miliomów (5 mΩ 1% 2 W) z wykorzystaniem samodzielnie zrobionego adaptera.

Natomiast fotografia B przedstawia pomiar rezystancji półcentymentrowego odcinka na pozór solidnej ścieżki na płytce drukowanej. Tu rezystancja jest wielokrotnie większa – ponad pół milioma. To też zgadza się z teorią: przy standardowej grubości warstewki miedzi 35 um, każdy kwadracik ścieżki ma rezystancję około 0,45 milioma.

Fotografia C pokazuje pomiar rezystancji na płytce stykowej. Katastrofa!!! Kilka miedzianych zworek i wewnętrzne połączenia płytki stykowej mają porażająco dużą rezystancję – prawie 1,3 oma!

Tu wspomnę, że dla uzyskania dokładnego wyniku pomiaru musiałem zwiększyć napięcie zasilania ponad 5 V, jednak w tym wypadku dążenie do dokładności ma niewielki sens, bo rezystancja takiego połączenia zmienia się po poruszeniu płytki i zworek. Niech fotografia C zachęci Cię do przeprowadzenia podobnych pomiarów! Właśnie dotykamy ogromnie ważnego zagadnienia: fatalnej niedoskonałości płytek stykowych tak ukochanych przez arduinowców. Takie nieoczekiwane rezystancje styków, ścieżek i przewodów mogą niekorzystnie wpływać na pracę układów elektronicznych. Do tego ważnego problemu będziemy wracać. W szczególności przyjrzymy się „arduinowym” płytkom stykowym.

Małe rezystancje i funkcja REL

W niektórych przypadkach wystarczy dobry omomierz. Ale nie najprostszy: po pierwsze taki z zakresem pomiarowym 200 omów lub mniej, po drugie koniecznie z funkcją REL według fotografii 1, który może zapamiętać „wartość zerową”, czyli rezystancję przewodów i styków, a potem mierzy tylko różnicę oporności. Jednak zakres pomiarowy jest wtedy bardzo ograniczony, a z kilku innych względów nie jest to rozwiązanie optymalne.

Jak mierzyć małe rezystancje?

Teoretycznie pomiar bardzo małych rezystancji jest dziecinnie łatwy: wykorzystując zasilacz przepuszczamy przez badaną rezystancję możliwie duży prąd o znanej wartości I i mierzymy spadek napięcia U na niej. Badana rezystancja ma wartość: R = U / I.

Nie każdy ma jednak odpowiednio potężny zasilacz i odpowiednio czuły woltomierz. Ale każdy posiada zasilacz 5 V o wydajności co najmniej 1 A, choćby od ładowarki smartfona. Opisywany przyrząd dołączamy do jakiegokolwiek zasilacza 5 V o wydajności minimum 1 A. Do zacisków pomiarowych dołączamy przewody prądowe lub dedykowaną przystawkę, pozwalające przez badaną rezystancję Rx przepuścić prąd o wartości dokładnie 1 A. Wykorzystując jakikolwiek zwyczajny woltomierz mierzymy napięcie na badanej rezystancji Rx. Wartość napięcia w woltach pokazuje wartość rezystancja Rx w omach.

Kalibrowane źródło prądowe

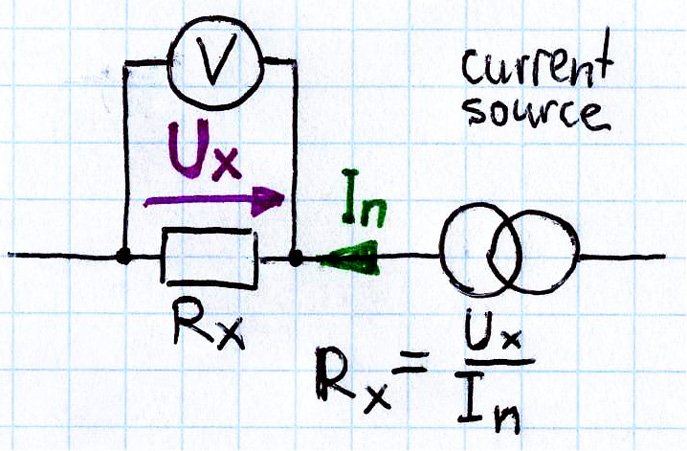
Bliski ideału jest sposób z wykorzystaniem kalibrowanego źródła prądowego (current source), czyli układu, który według rysunku 2 zapewni przepływ prądu In o dokładnie ustalonej wartości. Wtedy do pomiaru rezystancji wystarczy jeden woltomierz. Znając prąd In, badaną rezystancję RX obliczymy z zależności R = U / I. A gdy prąd In będzie miał „okrągłą” wartość 1 ampera, nie trzeba niczego liczyć, bo napięcie w (mili)woltach odpowiada rezystancji w (mili)omach. I właśnie taki układ chcemy zrealizować (o ile nie mamy laboratoryjnego zasilacza z precyzyjnym ogranicznikiem prądowym, który równie dobrze można do tego wykorzystać).

Moja propozycja jest taka: budujemy stabilne źródło prądowe, o wydajności jak najbardziej zbliżonej do 1 ampera. Nawet najprostszy, 3,5-cyfrowy woltomierz na najniższym zakresie 200 mV ma rozdzielczość 0,1 mV czyli 100 mikrowoltów, co pozwoli mierzyć rezystancje od 100 mikroomów wzwyż. Dolną granicę pomiaru wyznaczy czułość woltomierza. Warto więc postarać się o lepszy woltomierz, bo będziemy mogli mierzyć jeszcze mniejsze rezystancje i z lepszą dokładnością. Gdy zastosujemy woltomierz o rozdzielczości 1 mikrowolta, dolną granica pomiaru będzie 1 mikroom! Takie woltomierze są dostępne i to w atrakcyjnych cenach. Przykładem jest pokazany na fotografiach ANENG AN870 lub jego jeszcze tańszy odpowiednik.

Czteropunktowy układ Kelvina

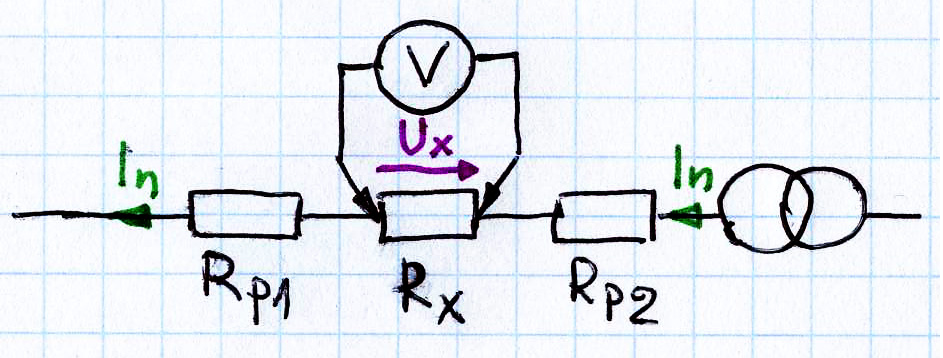
Problem w tym, że badana rezystancja RX może być porównywalna, a nawet mniejsza, od różnych niepożądanych rezystancji przewodów i styków, które wystąpią w obwodzie pomiarowym. Obecność takich niepotrzebnych szeregowych rezystancji nie stanowi żadnego problemu, gdy spadek napięcia UX jest mierzony bezpośrednio na rezystancji Rx. Z uwagi na różne szkodliwe rezystancje połączeń i styków, obowiązkowo trzeba wykorzystać czteropunktowe połączenie Kelvina. Jak ilustruje rysunek 3, woltomierz ma mierzyć napięcie tylko na badanej rezystancji, a więc mierzymy rezystancję między punktami dołączenia sond woltomierza.

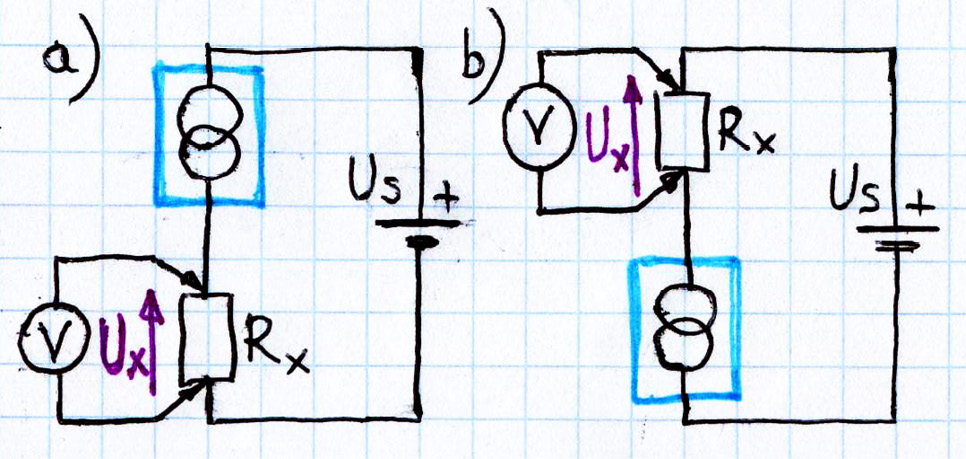
Jeżeli mamy niezależne, dwukońcówkowe źródło prądowe, to dwa sposoby jego wykorzystania, zilustrowane na rysunku 4, są równorzędne, jednakowo dobre, ale choćby tylko dla sentymentu, z przyzwyczajenia lub „na wszelki wypadek” wielu elektroników wolałoby zbudować wersję z rysunku 4a, gdzie badana rezystancja jest dołączana do ujemnego bieguna źródła zasilania, który zwykle taktowany jest jako masa. My też pójdziemy tą drogą.

Wybór koncepcji

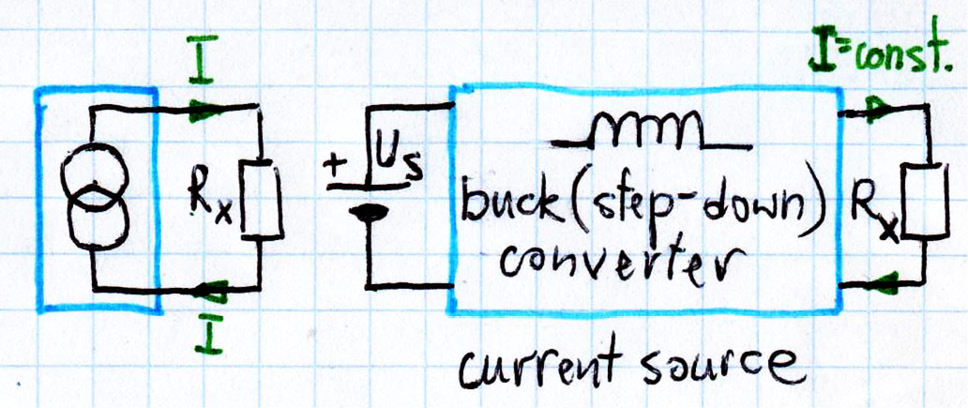
Potrzebne źródło prądowe można zrealizować na wiele sposobów. W układzie ma płynąć prąd 1 A, mierzona rezystancja będzie mniejsza niż 1 Ω, więc spadek napięcia UX nie przekroczy 1 V, a wydzielana moc strat będzie mniejsza niż 1 wat. Teoretycznie do zasilania wystarczyłoby jakieś 1-amperowe źródło prądowe, które dostarczy moc do 1 wata. Można coś takiego zrealizować, na przykład w postaci obniżającej przetwornicy impulsowej z wyjściem prądowym 1 A, według rysunku 5, jednak w praktyce, dla mniej zaawansowanych byłoby to dość trudne i kłopotliwe do realizacji. Podobnie kłopotliwy byłby sensowny układ oszczędnego liniowego źródła prądowego zasilanego dwoma napięciami.

Ponieważ ma to być realny, praktycznie użyteczny przyrząd pomiarowy, warto zbudować go tak, żeby był łatwy w obsłudze. Optymalna wydaje się z realizacja prostego modułu według rysunku 4a z łatwo dostępnym źródłem zasilania Us, na przykład zwykłym zasilaczem 5 V 1 A.

Jaka ma być dokładność?

Idea jest taka, że prąd pomiarowy ma mieć natężenie dokładnie 1 ampera. Ale z jaką dokładnością? I na ile ta wartość może zmieniać się pod wpływem takich czynników jak zmiany napięcia zasilania Us oraz zmiany temperatury?

Można zaprojektować bardzo precyzyjne i bardzo stabilne źródło prądowe. Tylko czy to konieczne?

Jednym z kluczowych czynników jest dokładność, czy raczej spodziewany błąd używanego do pomiarów woltomierza. Nie ma sensu, żeby źródło prądowe miało dokładność i stabilność dużo lepszą niż współpracujący woltomierz. A najbardziej popularne woltomierze mają według specyfikacji maksymalny błąd 0,5…1%, a tylko w bardzo nielicznych błąd pomiaru jest mniejszy niż 0,1%.

Koniecznie trzeba też wziąć pod uwagę, że projektowane źródło prądowe trzeba będzie wstępnie skalibrować za pomocą jakiegoś amperomierza. A tu z dokładnością zwykle jest gorzej. Amperomierze w popularnych miernikach bardzo rzadko mają dokładność lepszą niż 0,5%.

A tak w ogóle, to w przypadku bardzo małych rezystancji niezmiernie rzadko potrzebna jest wysoka dokładność, a często absolutnie wystarczy przybliżona wartość i dokładność pomiaru rzędu nawet 10%.

Nie ma więc głębszego sensu próba projektowania do takich celów bardzo precyzyjnego i bardzo stabilnego źródła prądowego. Zwłaszcza chodzi o stabilność cieplną: wystarczy, by ewentualne zmiany temperatury nie zmieniały prądu źródła prądowego więcej niż o 0,5%.

Taki wniosek umożliwia wykorzystanie prostych i tanich rozwiązań. Nie trzeba szukać specjalizowanych układów scalonych i troszczyć się o ich stabilność cieplną. Potrzebne nam źródło prądowe można zrealizować na bazie jakiegoś scalonego trzykońcówkowego stabilizatora napięcia. Dziś dostępnych jest mnóstwo stabilizatorów LDO, większość w małych obudowach SMD. Nam potrzebny jest prąd 1 A, a to zapowiada znaczącą moc strat, z którą maleńka obudowa SMD może sobie nie poradzić. Ponadto nie chodzi tylko o jak najmniejszy spadek napięcia LDO na stabilizatorze, ale też o kwestię, jakie w ogóle może być najmniejsze napięcie zasilania takiego stabilizatora prądu. Komplikuje to sytuację, dlatego zamiast sprawdzać w katalogach, czy uda się znaleźć odpowiedni stabilizator LDO, warto wrócić do bardzo do niedawna popularnego stabilizatora LM317. Nie będzie to rozwiązanie optymalne, ale za to bardzo proste i bardzo tanie.

Źródło prądowe na LM317

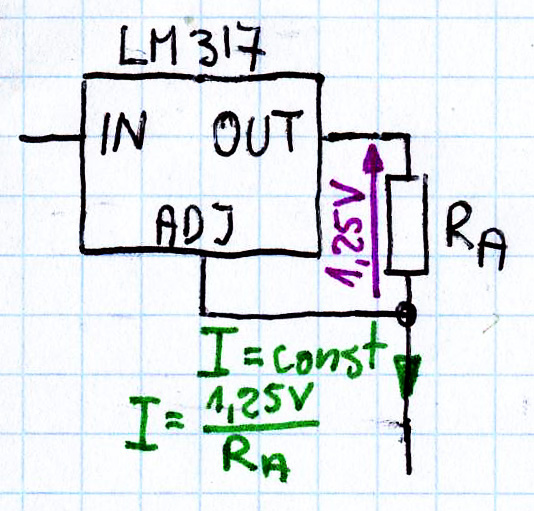
Stabilizator LM317, podobnie jak mnóstwo innych, pracuje na tej zasadzie, że stara się między wyjściem OUT i końcówka ADJ utrzymać napięcie 1,25 V. Wewnętrzny schemat kostki LM317, pokazany na rysunku 6 pochodzi z karty katalogowej OnSemi.

Uproszczony schemat stabilizatora widoczny jest na rysunku 7 (TI).

Pomaga on zrozumieć, dlaczego dodanie jednego rezystora według rysunku 8 pozwala zrealizować źródło prądowe o przyzwoitych parametrach.

W praktyce w omawianym zastosowaniu trzeba jeszcze rozważyć trzy podstawowe kwestie:

1 – jaki jest zakres użytecznych wartości napięcia zasilania Us?

2 – jak wygląda problem mocy strat stabilizatora?

3 – jak zmiany temperatury struktury zmienią prąd In?

Zakres napięć zasilania

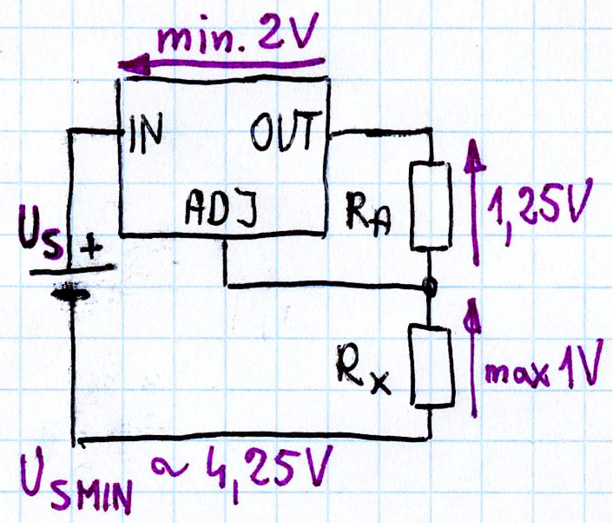
Chcemy przy prądzie In = 1 A mierzyć rezystancje poniżej 1 oma, a to znaczy, że spadek napięcia na badanej rezystancji RX będzie mniejszy niż 1 V. Do tego dojdzie spadek napięcia wymagany do prawidłowej pracy źródła prądowego ze starą kostką LM317. W katalogu znajdziemy rysunek 9, który pokazuje minimalny wymagany spadek napięcia ULDO między wejściem IN i wyjściem OUT.

Przy prądzie 1 A wymagane jest około 2 V. Do tego dojdzie 1,25 V spadku napięcia na rezystancji RA ustalającej prąd. I spadek napięcia na badanej rezystancji RX, od 0 do co najwyżej 1 V. W sumie zgodnie z rysunkiem 10 daje to minimalne napięcie zasilania USMIN = 4,25 V, co daje szansę na wykorzystanie dowolnego zasilacza 5 V 1 A.

Problem mocy strat

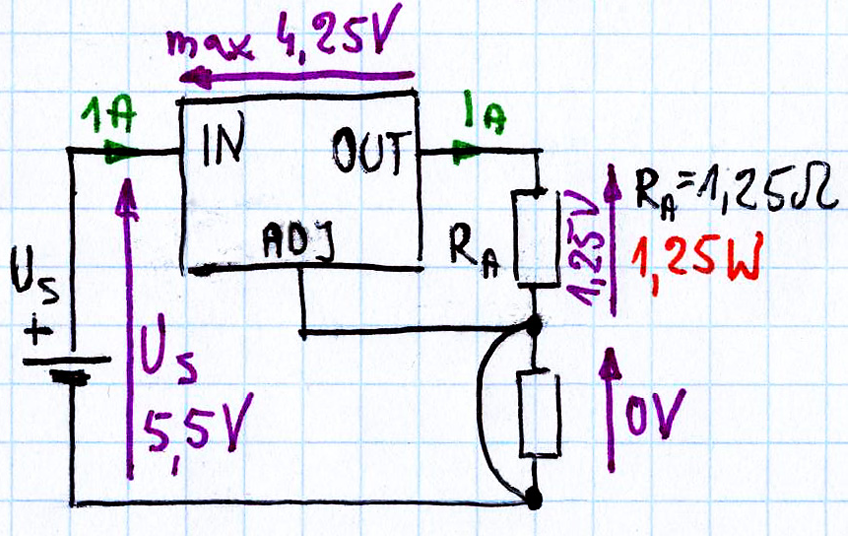
Stabilizator LM317 według katalogu ma maksymalną moc strat ponad 20 watów, ale tylko przy zastosowaniu bardzo skutecznego radiatora. My chcemy zrealizować jak najprostsze i najtańsze źródło prądowe, więc chcielibyśmy zastosować jakiś nieduży radiator. Zasilanie całości napięciem 5 V daje taką możliwość. Jak pokazuje rysunek 11, w najgorszym przypadku przy US = 5,5 V na samym stabilizatorze wystąpi napięcie 4,25 V i wydzieli się moc 4,25 W. To nie jest dużo. Nawet bez żadnego radiatora LM317 może rozproszyć do 2 watów.

W omawianym zastosowaniu w zasadzie wystarczy więc nieduży radiator, teoretycznie nawet w postaci małego kawałka blaszki, ale podczas pracy blaszka mogłaby mieć temperaturę ponad +100°C. Aby temperatura zbytnio nie rosła, trzeba zastosować radiator znacznie większy i skuteczniejszy niż absolutne minimum. Dla bezpieczeństwa użytkownika dobrze byłoby, gdyby podczas pracy radiator nie był gorący, żeby go można dotknąć ręką. To polepszy też stabilność cieplną prądu pomiarowego In.

Odnotowujemy też, że prąd 1 A, płynąc przez rezystancję RA = 1,25 Ω spowoduje wydzielenie w niej znacznej mocy strat 1,25 W.

Stabilność źródła prądowego

Oczywiście wartość prądu In nie będzie idealnie stabilna. Będzie się nieco zmieniać przy zmianach napięcia występującego na stabilizatorze oraz przy zmianach temperatury jego struktury. A temperatura struktury będzie zależeć od wielkości radiatora. Karta katalogowa nie zawiera informacji o stabilności źródła prądowego z LM317. Pokazane na rysunku 12 pokrewne dane dotyczące stabilności napięcia wyjściowego w funkcji zmian napięcia zasilania sugerują, że stabilność powinna być bardzo dobra.

Problem jednak w tym, że dotyczy to spadku napięcia na stabilizatorze co najmniej 3 V, a my chcemy pracować przy możliwie najmniejszym spadku napięcia na LM317, a wtedy stabilność prądu zapewne będzie gorsza – to koniecznie trzeba sprawdzić praktycznie w modelu, by określić minimalne napięcie zasilania. A jeżeli chodzi o stabilność cieplną, to katalog zawiera rysunek 13. Wynika z niego, że przy zmianie temperatury struktury stabilizatora od +25°C do +150°C napięcie referencyjne (i prąd źródła prądowego zmniejsza się z 1,25 V do 1,24 V, czyli o 0,8%. Tu widać powód, wręcz konieczność, zastosowania na tyle skutecznego radiatora, żeby stabilizator LM317 nie był aż tak gorący.

Dobór rezystora ustalającego prąd

Teoretycznie napięcie odniesienia LM317 wynosi 1,25 V, można zaniedbać prąd końcówki ADJ (około 50 uA), więc dla uzyskania prądu 1 A potrzebna jest rezystancja RA = 1,25 Ω. Jednak z uwagi na rozrzut wartości napięcia odniesienia (1,2…1,3 V, a może nawet więcej) trzeba przewidzieć możliwość korekcji rezystancji wyznaczającej prąd o kilka procent.

Prąd 1 A płynąc przez rezystancję 1,25 Ω spowoduje wydzielenie się mocy strat cieplnych 1,25 W (P = I2R). Jeżeli zastosujemy tu jakiś zwyczajny, tani rezystor RA, to podczas nagrzewania mocą 1,25 W jego rezystancja będzie się zmieniać, a to zmieni prąd In. Pamiętajmy, że przy maksymalnej mocy strat, rezystor może się nagrzać nawet do ponad +100°C. Po pierwsze wymaga to zastosowania rezystora lub raczej zestawu rezystorów o odpowiedniej obciążalności, co najmniej 2 W. Po drugie, przy takim prądzie trudno wyobrazić sobie sensowną korekcję rezystancji potencjometrem

Jeżeli układ ma być tani i zrealizowany z łatwo dostępnych elementów, najprościej ustalić wartość prądu za pomocą zestawu popularnych rezystorów. Małe rezystory do montażu przewlekanego (THT) zwykle mają obciążalność 0,2…0,6 W. Satysfakcjonujące wydaje się wykorzystanie ośmiu połączonych równolegle popularnych rezystorów 10-omowych, co daje rezystancję 1,25 V i obciążalność 1,6…4,8 W.

Parametry wersji budżetowej

Chcemy pozostawić możliwość zastosowania nawet najpopularniejszych rezystorów, być może o słabych parametrach, w tym o słabym, dużym współczynniku cieplnym (TCR), a to rodzi znaczący problem. Ja podczas pierwszych testów wykorzystałem zestaw zwyczajnych 8 rezystorów 10-omowych, pokazany na fotografii 14. Ich samonagrzewanie znacząco zmieniało prąd In: tuż po włączeniu wynosił on 0,95 A, a przy ciągłej pracy wskutek wzrostu ich temperatury wzrastał do 1,008 A. Aby z powodzeniem wykorzystać także takie, nawet najtańsze, rezystory należy zastosować zestaw, który będzie się mniej grzał – sensowne wydaje się wykorzystanie na przykład równolegle połączonych 17 sztuk rezystorów o popularnym nominale 22 Ω, co daje rezystancję około 1,3 Ω, a do tego trzeba dobrać jeszcze jeden lub dwa rezystory o innym nominale, żeby w tak łatwy sposób finalnie ustawić prąd pomiarowy dokładnie równy 1 A. W moim modelu trzeba było dodać rezystor 62 Ω. W takim zestawem 18 rezystorów tuż po włączeniu prąd wynosił 0,997 A i przy nagrzewaniu tych rezystorów stopniowo rósł do 1,005 A, co daje błąd poniżej ±0,5%.

Ty możesz trafić lepszy lub gorszy egzemplarz LM317, więc koniecznie sprawdź, jak obniżanie napięcia zasilania zmniejsza prąd In. U mnie przy RX = 0 (zwarcie), prąd zmniejszył się do wartości 0,995 A (błąd 0,5%) przy napięciu 4,05 V. Przy zasilaniu 5,0 V napięcie UX może sięgać 0,95 V, czyli moim mikroomomierzem można dokładnie mierzyć rezystancje do około 0,9 oma z błędem do 0,5% (pomijając błąd woltomierza). Zakres pomiarowy będzie też mniejszy, gdy napięcie zasilacza będzie mniejsze niż 5,0 V. Ja wykorzystuję 5-woltowy zasilacz o prądzie większym niż 1 A. Jeżeli Ty wykorzystasz zasilacz dokładnie 1-amperowy to koniecznie sprawdź, czy przy jego napięcie nie zmniejsza się zbytnio (poniżej 4,5 V) – wtedy niestety nie nadawałby się do naszych celów. Wszystko to możesz sprawdzić jednocześnie, włączając amperomierz w szereg z badaną rezystancją RX. Sprawdź prąd gdy RX = 0 (zwarcie), a potem zastosuj RX o wartości powiedzmy 0,1 Ω, 0,22 Ω, 0,47 Ω, 1 Ω i ewentualnie większe. Sprawdź przy jakiej rezystancji RX prąd zmaleje o 0,5%…1% – to jest górna granica dokładnych pomiarów.

Fotografia A na początku artykułu pokazuje pomiar zakupionego kiedyś w TME rezystora, pokazanego dokładniej na fotografii 15 (Walsin WW25; 5 mΩ; 2 W; ±1%).

Nie znaczy to wcale, że zmierzyliśmy jego rezystancję z dokładnością 1 mikrooma, bo to oznaczałoby dokładność 0,02%. Realną dokładność naszego pomiaru wyznacza nie tylko dokładność kalibracji i stabilność źródła prądowego (rzędu ±0,5%), ale też ewentualne inne źródła niepewności. Najogólniej biorąc – rezystor o tak małej mocy po wlutowaniu w układ na pewno wykaże nieco inną rezystancję niż zmierzyliśmy. Precyzyjne pomiary przed wlutowaniem w układ nie mają praktycznego sensu – jeśli już, to po zamontowaniu na miejscu pracy. Ale faktem jest, że woltomierzem o rozdzielczości 1 mikrowolta możemy mierzyć rezystancje już od 1 mikrooma.

Realizacja

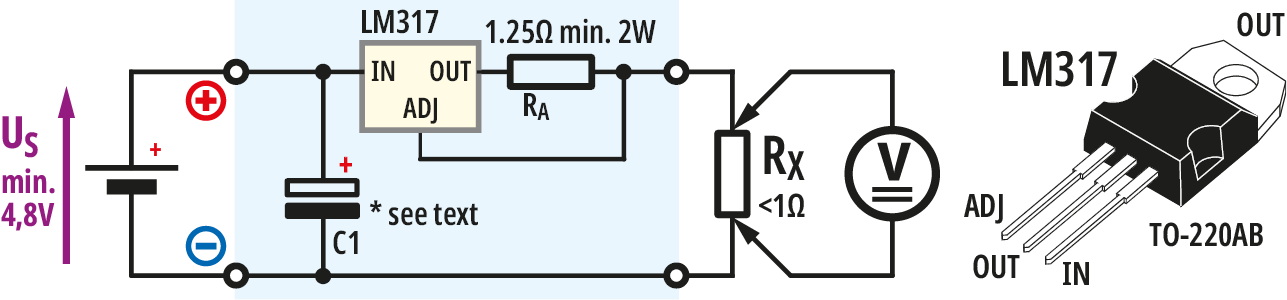
Źródło prądowe zrealizowałem według rysunku 16.

Ponieważ nie było tendencji do samowzbudzenia, więc nie zastosowałem kondensatora C1, ale na wszelki wypadek, dla uniknięcia ryzyka samowzbudzenia można go dodać (10…100 uF).

Realizacja mojego prostego i taniego źródła prądowego pokazana jest na fotografii tytułowej oraz na fotografiach 17, 18.

Małe rezystory tworzące RA podczas pracy są mocno ciepłe. Natomiast mój radiator jest stosunkowo duży i nawet przy ciągłej pracy grzeje się bardzo mało – jest letni. Przykręcając stabilizator LM317 do radiatora warto miejsce połączenia posmarować smarem termicznym. Ja do radiatora przymocowałem też zaciski śrubowe (wystarczą cztery). W dwa środkowe zamocowałem sprężynujące pręciki o przekroju kwadratowym, które tak wygiąłem, żeby pozwoliły na wygodne testowanie rezystorów SMD, obowiązkowo czteropunktową metodą Kelvina, co pokazuje fotografia wstępna.

Co można poprawić?

Jeszcze mniejsze rezystancje można byłoby mierzyć po zwiększeniu prądu pomiarowego powyżej 1 ampera, co jednak rodzi szereg problemów. Nawet najprostszy woltomierz cyfrowy może mierzyć napięcie od 0,1 miliwolta, czyli rezystancje od 100 mikroomów. Jeżeli ktoś koniecznie chce mierzyć rezystancje jeszcze mniejsze (lub z większą dokładnością), niech po prostu wykorzysta lepszy woltomierz. Fotografie w artykule pokazują pomiar napięcia z rozdzielczością 1 mikrowolta, co teoretycznie pozwala mierzyć rezystancje już od 1 mikrooma i z rozdzielczością 1 mikrooma.

W zasadzie tak, ale z tą „większą dokładności” przy pomiarach skrajnie małych rezystancji może być kłopot z zupełnie innych względów – najprościej biorąc, wyniki najprawdopodobniej nie będą powtarzalne.

Układ byłby najbardziej uniwersalny, gdyby był zasilany bateryjnie. Przystępując do projektowania zastanawiałem się, czy układ można byłoby zasilać z jednego akumulatora Li-Ion, którego napięcie nominalne to wprawdzie 3,7 V, ale który po naładowaniu ma 4,2 V. Ponieważ napięcie akumulatora pod obciążeniem zmniejsza się, więc byłoby to ryzykowne. A dodawanie przetwornicy podwyższającej to kiepski pomysł, bo jeśli już stosować przetwornicę, to obniżającą, która jednocześnie będzie źródłem prądowym. W razie zainteresowania, nad taką bateryjną wersją można byłoby pomyśleć.

Parametry opisywanego źródła prądowego nie są rewelacyjne, jednak jak na układ zrealizowany z najpopularniejszych elementów są zupełnie przyzwoite. Dla polepszenia stabilności cieplnej można byłoby zastosować lepszej jakości rezystory (metalizowane, o tolerancji 1%) lub rezystory o większej obciążalności, żeby ich temperatura rosła mniej. Przy pomiarze rezystancji cewek potrzebny będzie kondensator C1 z rysunku 16.

Na koniec prośba: jeżeli za pomocą takiej przystawki albo w jakikolwiek inny sposób przeprowadzisz pomiary bardzo małych rezystancji i wyniki Cię zaskoczą – ucieszą lub zasmucą, podziel się proszę swoim doświadczeniem. Jeżeli interesuje Cię kwestia odpowiedniego multimetru – daj znać, tematyką multimetrów zajmiemy się dużo szerzej, ze szczegółami. Poinformuj mnie też, jeżeli jesteś zainteresowany przeróbką zasilaczy impulsowych, między innymi w celu realizacji oszczędnego impulsowego źródła prądowego.

Do kontaktu możesz wykorzystać stronę

Zapytaj, odpowiedz

albo e-mail kontakt@piotr-gorecki.pl. ©

Piotr Górecki

Zrób to sam, czyli DIY – Do It Yourself!

Zachęcam wszystkich Czytelników, a więc także i Ciebie, do naśladowania, kontynuacji, ulepszenia oraz do przedstawienia ładniejszych i lepszych niż moja realizacji tego projektu.

Zapraszam do zaprezentowania fotografii i innych informacji o swojej własnej wersji. Wtedy będzie można porównać sposoby realizacji nie tylko „kto ładniej?”, ale też „kto bardziej praktycznie?”.

Czy może usprawnisz ten układ lub zaproponujesz lepszy, pełniący taką samą lub podobną funkcję?

A może znajdziesz i ewentualnie usuniesz jakieś istotne wady zaprezentowanego rozwiązania?

Twoje informacje mogą pojawić się jako komentarz na stronie, albo jako oddzielny artykuł w czasopiśmie. Napisz do mnie: kontakt@piotr-gorecki.pl

Zachęcam do działania! Zapraszam do współpracy!