PKE – Praktyczny Kurs Elektroniki (10) Iluminofonia
Na powyższej fotografii tytułowej pokazany jest układ Iluminofonii. Dwie pracujące równolegle diody LED zaświecają się, gdy do mikrofonu dotrą głośniejsze dźwięki o średnich częstotliwościach. Fotografia wstępna pokazuje wersję jednokanałową z filtrem średnich częstotliwości. W układzie można zastosować filtr o innych parametrach.
Opis układu dla „zaawansowanych”
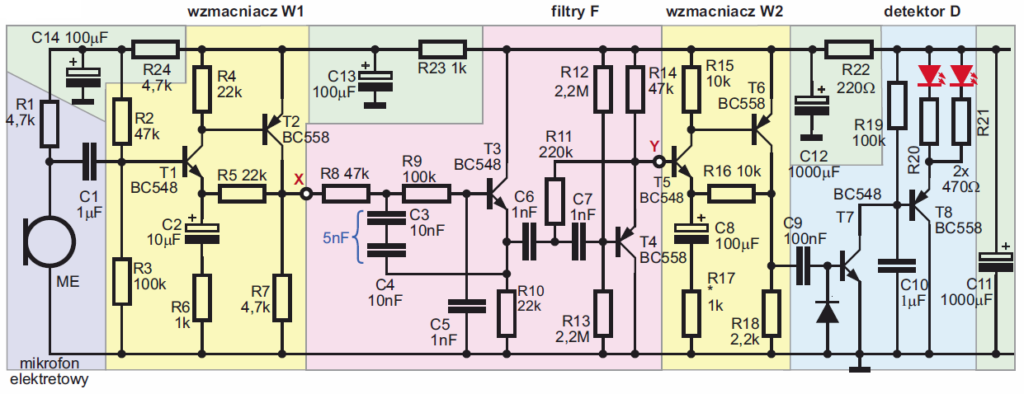
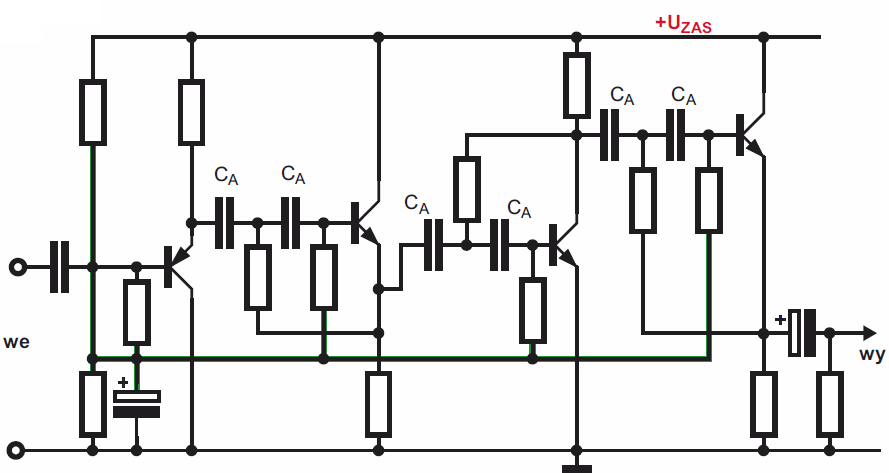
Schemat ideowy Iluminofonii z fotografii tytułowej pokazany jest na rysunku A. Na schemacie żółtymi podkładkami wyróżnione są dwa wzmacniacze przebiegów zmiennych (W1, W2). Taką konfigurację wykorzystywaliśmy w ostatnim układzie poprzedniego wykładu. Wzmocnienie tych wzmacniaczy wyznaczone jest przez wartość rezystorów R6 i R17 (a właściwie stosunki R5/R6 oraz R16/R17). Różową podkładką wyróżniony jest obwód filtru F, a właściwie dwóch kaskadowo połączonych filtrów: dolnoprzepustowego z tranzystorem T3 i górnoprzepustowego (T4). Podkładka niebieska wyróżnia obwód detektora aktywnego i sterownika diod LED.
Zasada działania jest bardzo prosta – silniejsze dźwięki powodują zaświecanie diod LED. Sygnał z właściwie spolaryzowanego mikrofonu elektretowego ME jest wstępnie wzmacniany we wzmacniaczu W1, potem filtr F przepuszcza tylko sygnały z określonego pasma częstotliwości – w tym przypadku przepuszcza średnie tony, natomiast tłumi i tony niskie, i wysokie. Przepuszczone sygnały są dodatkowo wzmacniane we wzmacniaczu W2. Sygnały o amplitudzie powyżej 0,6 V przechodzą przez C9 i powodują otwieranie tranzystora T7, który pracuje tu w roli detektora. Otwarcie tranzystora T7 nawet na krótki czas rozładowuje C10, który potem pomału ładuje się przez R19, zapobiegając zbyt szybkiemu migotaniu diod. Obniżenie napięcia na kolektorze T7 i na C10 powoduje przewodzenie T8 i zaświecenie diod LED.
Zwróć uwagę na wyróżnione zielonymi podkładami obwody filtracji zasilania, niezbędne w układach o dużym wzmocnieniu.
Montując układ, nie zapominaj o prawidłowym umieszczeniu elementów biegunowych, w tym mikrofonu elektretowego ME, którego wyprowadzenie ujemne połączone jest z obudową – szczegóły podane były w poprzednim wykładzie.
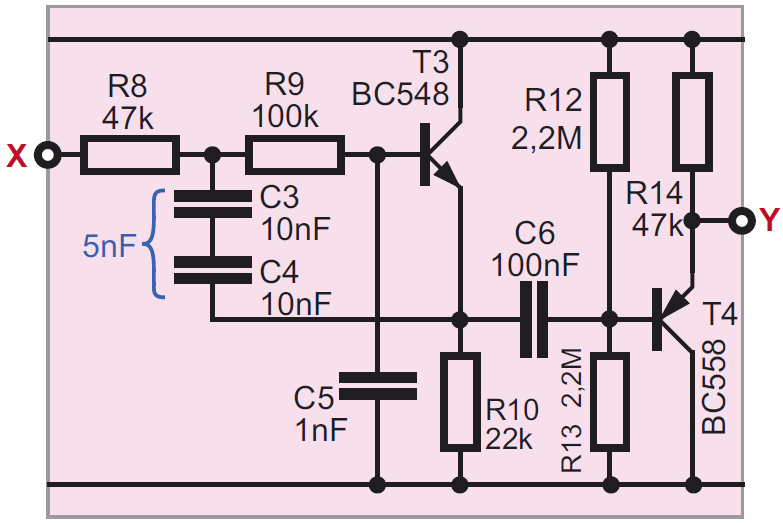
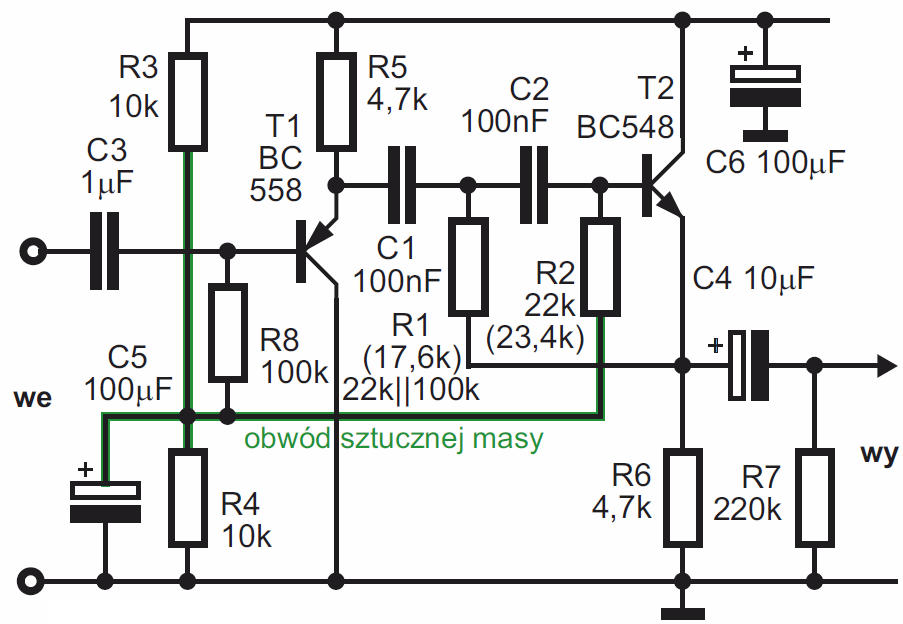
Wersja z rysunku A i fotografii tytułowej reaguje na tony średnie. Układ można łatwo zmodyfikować, by reagował na tony niskie. Rysunek B pokazuje zmodyfikowany obwód filtru F, gdzie filtr dolnoprzepustowy ma częstotliwość graniczną około 130 Hz. Moglibyśmy całkowicie zrezygnować z filtru górnoprzepustowego, ale pozostawiamy tranzystor T4 tylko dlatego, by zachować optymalne napięcia stałe w obwodzie wzmacniacza W2. Obwód C6+R12+R13 wprawdzie jest filtrem górnoprzepustowym, ale o częstotliwości granicznej około 1,6 Hz, więc na pewno nie ogranicza pasma akustycznego, które zaczyna się od 16…20 Hz.
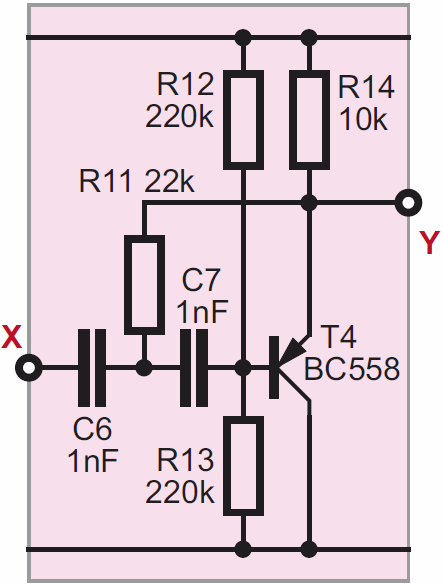
Aby natomiast iluminofonia reagowała na tony wysokie, wystarczy zmodyfikować filtr według rysunku C. Tu mamy wyłącznie filtr górnoprzepustowy (o częstotliwości granicznej około 2,5 kHz). W takich wersjach zapewne warto zmienić też kolor diod LED.
W każdej wersji trzeba będzie prawdopodobnie dobrać wzmocnienie W2 za pomocą rezystora R17 (100 Ω…10 kΩ), by uzyskać zbliżoną czułość dla wszystkich pasm częstotliwości. Z kolei dynamikę świecenia diody można zmienić według upodobania, zmieniając pojemność C10 (0 nF, 10 nF 100 nF, 1 uF) i rezystancję R19 (22 kΩ…220 kΩ). Jasność diod LED można zmieniać za pomocą rezystorów R20 i R21 (220 Ω…1 kΩ), pamiętając, że czym jaśniej świecą diody, tym szybciej rozładuje się mała bateria 9-woltowa. Taki układ lepiej byłoby zasilać z akumulatora lub z zasilacza stabilizowanego.
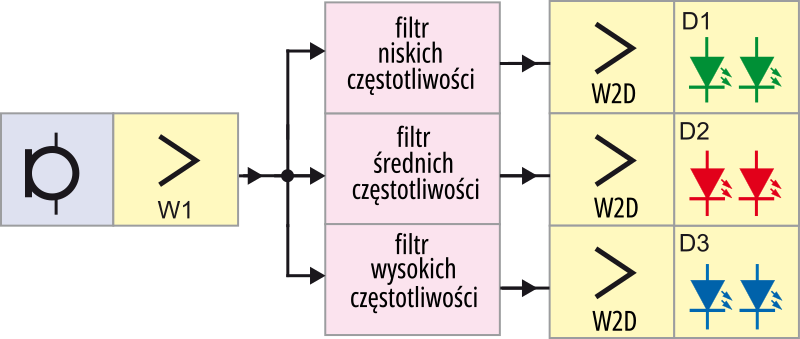
Kto ma więcej elementów, może zbudować iluminofonię trzykanałową według idei z rysunku D. Mikrofon i wzmacniacz W1 pozostaną wspólne. Trzeba tylko zwielokrotnić zespoły filtrów F według rysunków B i C, wzmacniacza W2 i detektora D.
Poznajemy elementy i układy elektroniczne
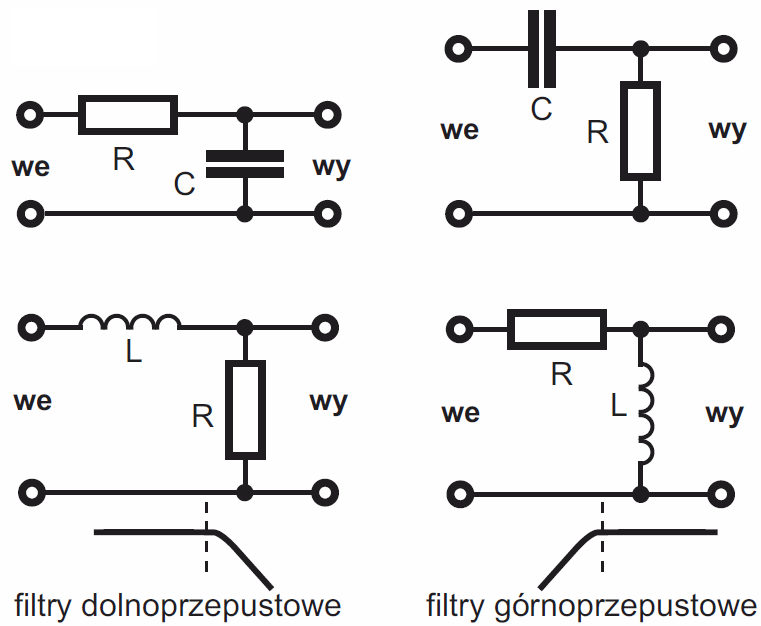
Filtry. Wcześniej mówiliśmy, że dla częstotliwości wysokich kondensator stanowi zwarcie, a dla częstotliwości bardzo niskich i dla prądu stałego – przerwę. To ogromne uproszczenie! W poprzednim wykładzie nieco uściśliliśmy to zagadnienie. Wiemy, że reaktancja kondensatora i cewki liniowo zmienia się z częstotliwością, a w skali podwójnie logarytmicznej wykresem jest linia prosta. Wiemy też już, że dzielnik zawierający rezystor i kondensator jest filtrem RC, przepuszczającym i tłumiącym sygnały o różnych częstotliwościach. Poznaliśmy prosty filtr RC dolnoprzepustowy i górnoprzepustowy – zobacz rysunek 10 w poprzednim wykładzie. Analogicznie można byłoby zrealizować filtry dolno i górnoprzepustowe RL z użyciem cewek, jak pokazuje rysunek 1.
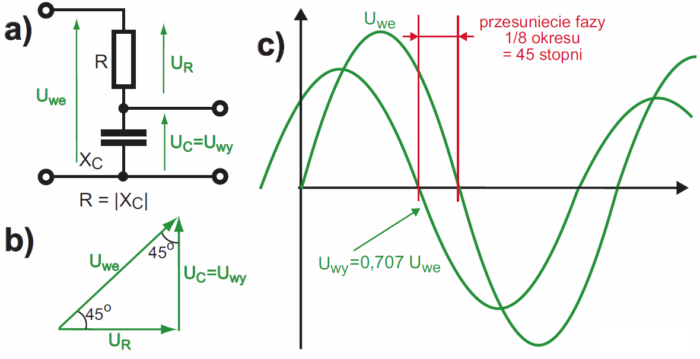
W praktyce tego nie robimy z uwagi na liczne wady cewek. Wykorzystujemy natomiast powszechnie obwody RC, nie zawsze traktując je zresztą jako filtry. Rozszerzmy informacje z poprzedniego wykładu: w takich obwodach (filtrach) przy jakiejś częstotliwości f liczbowa wartość reaktancji X staje się równa rezystancji R. W przypadku filtrów RC mamy XC = 1/2π, więc umowna częstotliwość graniczna ma wartość fg = 1/ 2πRC. Przy tej właśnie częstotliwości XC = R, jak dla filtru dolnoprzepustowego pokazuje rysunek 2a. Pomimo równości XC = R, z uwagi na przesunięcie fazy w kondensatorze, napięcie wyjściowe nie jest dwa razy mniejsze od napięcia wejściowego, tylko stanowi około 0,707 napięcia wyjściowego (dokładnie jest pierwiastek z dwóch razy mniejsze). Ilustruje to graficznie rysunek 2b. Te 0,707 wartości napięcia wyjściowego to w mierze logarytmicznej –3 dB (dokładniej biorąc –3,103 dB). Co ważne, wyjściowy przebieg sinusoidalny o częstotliwości fg jest przesunięty względem wejściowego dokładnie o 45 stopni, co jest zilustrowane na rysunku 2c.
A tak przy okazji: zapamiętaj, że we wszystkich filtrach jako częstotliwość graniczną przyjmujemy taką, przy której sygnał jest tłumiony o 3 dB. Znormalizowaną charakterystykę amplitudową omawianych prostych filtrów RC (oraz RL) poznałeś w poprzednim wykładzie na rysunku 10d.
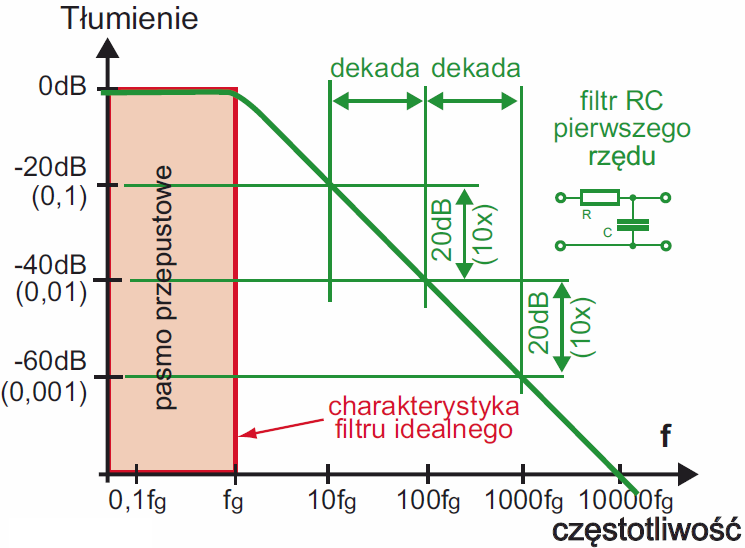
Ideałem byłby filtr o dokładnie prostokątnej charakterystyce, narysowanej kolorem czerwonym na rysunku 3.
Taki filtr w paśmie przepustowym miałby tłumienie równe zeru – przepuszczałby pożądane sygnały, a w paśmie zaporowym miałby tłumienie nieskończenie wielkie. Idealnych filtrów nawet nie próbujemy realizować. Poznane proste filtry RC, choć bywają bardzo często wykorzystywane, nie są zbyt skuteczne, czyli mają małą stromość zbocza charakterystyki. Ich tłumienie wzrasta dwukrotnie przy dwukrotnej zmianie częstotliwości, czyli 6 decybeli na oktawę (6 dB/okt.), a dziesięciokrotnie przy dziewięciokrotnej zmianie częstotliwości, czyli 20 decybeli na dekadę (20 dB/dek.). Ilustruje to zielona charakterystyka na rysunku 3. Są to tak zwane filtry pierwszego rzędu. Często potrzebne są skuteczniejsze filtry o ostrzejszych, bardziej stromych zboczach. W praktyce skutecznych filtrów nie realizujemy przez kaskadowe połączenie kilku jednakowych sekcji według rysunku 4, ponieważ przy takim połączeniu poszczególne sekcje wpływają na siebie i efekt byłby daleki od oczekiwanego. Problem między innymi w tym, że każda następna sekcja stanowi obciążenie dla poprzedniej.
Zagadnienia związane z bardziej złożonymi, „ostrzejszymi” filtrami są bardzo trudne, a zrozumienie ich właściwości wymaga znajomości wyższej matematyki. Nie sposób tego krótko wytłumaczyć. Przyjmij tylko do wiadomości, że istnieje mnóstwo odmian najróżniejszych filtrów, gdzie częstotliwość wyznaczają odpowiednio dobrane elementy RC, a właściwości są znakomicie poprawione przez zastosowanie wzmacniaczy. Takie filtry RC ze wzmacniaczami nazywamy filtrami aktywnymi.
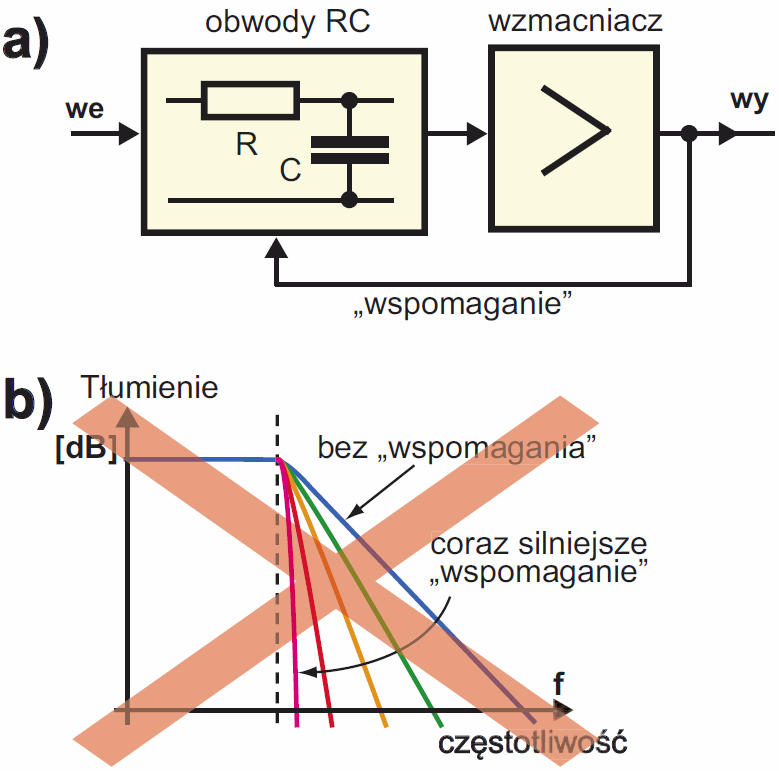
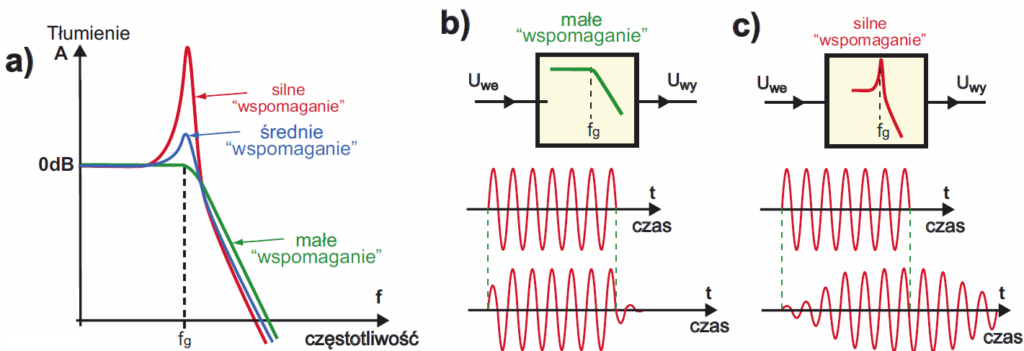
Można w uproszczeniu powiedzieć, że filtr aktywny to filtr RC „wspomagany” wzmacniaczem, co dla filtru dolnoprzepustowego można zobrazować na rysunku 5a. Ale tu od razu trzeba przestrzec przed błędnym wyobrażeniem. Otóż początkujący często wyobrażają sobie, że czym większe, silniejsze jest to „wspomaganie”, tym bardziej strome jest zbocze charakterystyki amplitudowej filtru. Takie błędne wyobrażenie zobrazowane jest na (przekreślonym) rysunku 5b.
W rzeczywistości silniejsze „wspomaganie” praktycznie nie zmienia nachylenia zbocza charakterystyki, a za to ma silny wpływ na inne ważne właściwości. Otóż po pierwsze przy silnym „wspomaganiu”, na skraju charakterystyki amplitudowej, w okolicy częstotliwości granicznej fg pojawia się tzw. podbicie – niepożądany garb, jak pokazuje w uproszczeniu rysunek 6a. Po drugie mówimy, że filtr zaczyna „dzwonić”, to znaczy drgania o częstotliwościach zbliżonych do granicznej fg utrzymują się w nim po zaniku sygnału wejściowego, co z kolei ilustruje rysunek 6b oraz rysunek 6c. Najczęściej silne „wspomaganie” nie jest więc pożądane, a jest wręcz wadą.
W praktyce, aby uzyskać filtr o większej stromości zboczy, łączymy kaskadowo kilka odpowiednio dobranych „sekcji RC”. W najprostszym przypadku można poprawić stromość, stosując jednakowe sekcje RC i bufory (wtórniki) pośredniczące według rysunku 7.
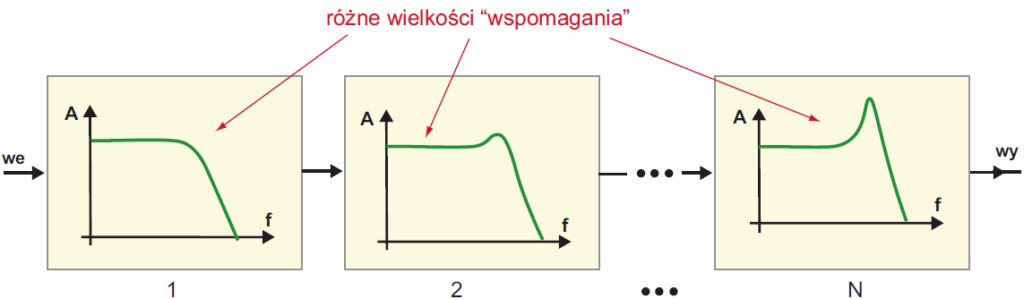
W ten sposób moglibyśmy poprawić stromość zbocza filtru, uzyskując nachylenie n×20 dB/dekadę, ale w większości zastosowań nie jest to optymalny sposób, choćby z uwagi na nieoptymalny przebieg charakterystyki w pobliżu częstotliwości granicznej fg. Filtry o dużej stromości zboczy realizujemy nieco inaczej. W praktyce powszechnie wykorzystuje się liczne odmiany filtrów aktywnych, gdzie podstawowa „sekcja – cegiełka” to tak zwany filtr drugiego rzędu, który daje stromość charakterystyki 40 dB/dek, czyli 12 dB oktawę, co odpowiada złożeniu dwóch ogniw RC. Łączymy kaskadowo kilka takich „cegiełek” drugiego rzędu według rysunku 8, przy czym zależnie od pożądanych parametrów całości dotyczących podbicia i „dzwonienia”, cegiełki te nie są identyczne, tylko różnią się wartościami elementów.
Przykład pokazany jest w uproszczeniu na rysunku 9.
W praktyce bardzo często wystarczają filtry drugiego rzędu, ale można też spotkać filtry 20. rzędu, czyli zawierające aż dziesięć „cegiełek”. Nie zaszkodzi wiedzieć, że dziś oprócz omawianych właśnie filtrów analogowych, coraz częściej wykorzystuje się ich odpowiedniki cyfrowe, gdzie rolę filtru odgrywa odpowiedni program – to jednak zupełnie oddzielne zagadnienie.
Spośród niezliczonych odmian filtrów aktywnych my na razie wspomnijmy tylko o jednym ich rodzaju. Fachowo bywają one nazywane filtrami Sallena-Keya i są odmianą tzw. filtrów ze źródłem sterowanym (VCVS). My wykorzystajmy proste rozwiązanie, gdzie wzmacniaczem jest… zwyczajny wtórnik, a mianowicie tranzystor pracujący w układzie OC.
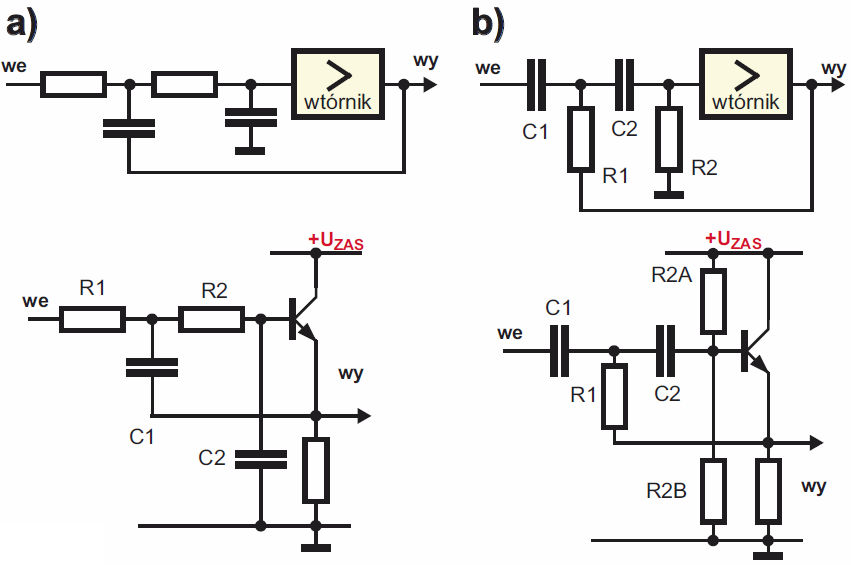
Rysunek 10a pokazuje schemat filtru dolnoprzepustowego. „Wspomaganie” z wyjścia do obwodów RC realizowane jest tu przez kondensator C1. Analogicznie rysunek 10b przedstawia filtr górnoprzepustowy.
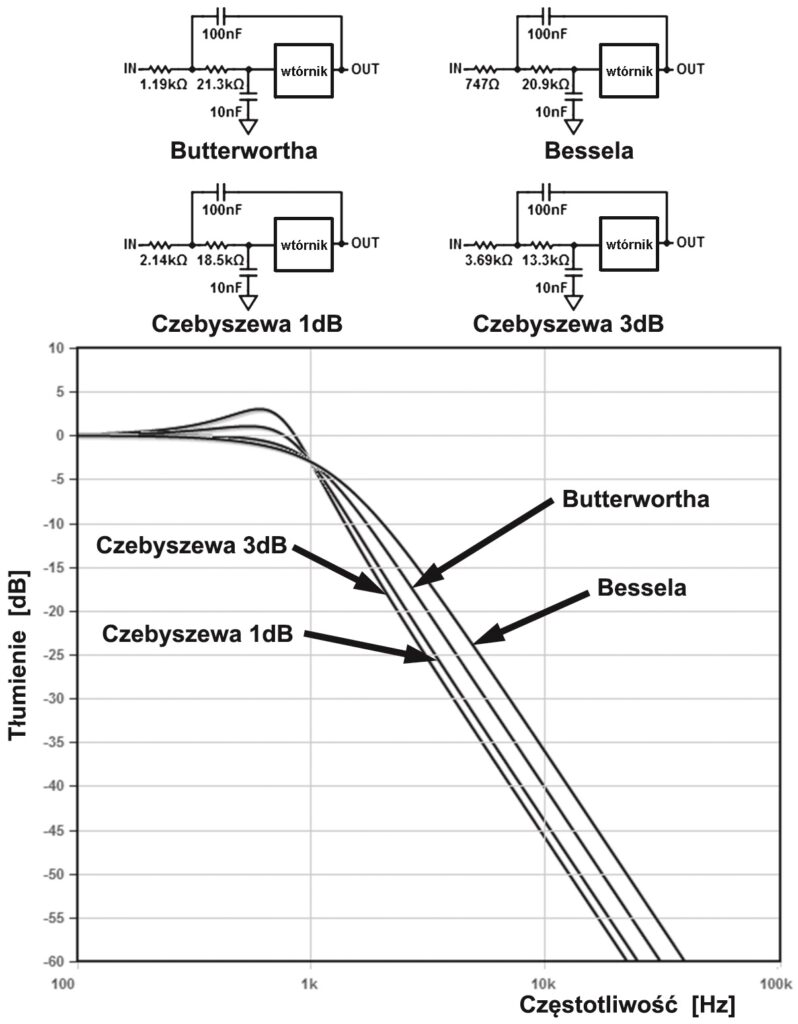
Zasadniczo wystarczyłby tylko jeden rezystor R2, ale w praktycznej realizacji tranzystor musi być spolaryzowany, więc dajemy dwa jednakowe rezystory R2A i R2B, które dodatkowo wyznaczają punkt pracy tranzystora. Dobierając odpowiednio wartości obu ogniw RC, ustalamy zarówno częstotliwość graniczną, jak też wielkość „wspomagania”, optymalną dla danego zastosowania. Istnieje nieskończenie wiele kombinacji wartości elementów, które dają użyteczne charakterystyki. Rysunek 11 pokazuje przebieg najpopularniejszych, niejako standardowych charakterystyk amplitudowych filtrów przy różnej wielkości (niewielkiego) „wspomagania” – filtry o takim przebiegu charakterystyk nazywane są od nazwisk wynalazców filtrami Bessela, Butterwortha i Czebyszewa. Charakterystyka Butterwortha jest najbardziej płaska. Filtry Czebyszewa mają zafalowania charakterystyki, ale też nieco lepsze tłumienie sygnałów niepożądanych. Natomiast filtry o charakterystyce Bessela wprawdzie mają nieco słabsze tłumienie sygnałów niepożądanych, ale za to najwierniej przenoszą impulsy i dlatego dobrze nadają się do układów audio.
A teraz przejdźmy do praktyki. Rysunek 12 i fotografia 13 pokazują prosty filtr dolnoprzepustowy do subwoofera (o charakterystyce Bessela), uzupełniony wtórnikiem wejściowym na tranzystorze T1.
Częstotliwość graniczna wynosi około 160 Hz i można ją modyfikować, proporcjonalnie zmieniając pojemności C1, C2 (C1=10×C2). Zapamiętaj, że w tego rodzaju filtrach trzeba stosować dobrej jakości kondensatory – foliowe, natomiast kondensatory ceramiczne o pojemności większej od 1 nF, w tym nasze lizaczki” 100 nF, najczęściej mają małą stabilność i do takich filtrów się nie nadają. Mało stabilne ceramiczne „lizaczki” 100 nF nadają się natomiast znakomicie do filtracji obwodów zasilania.
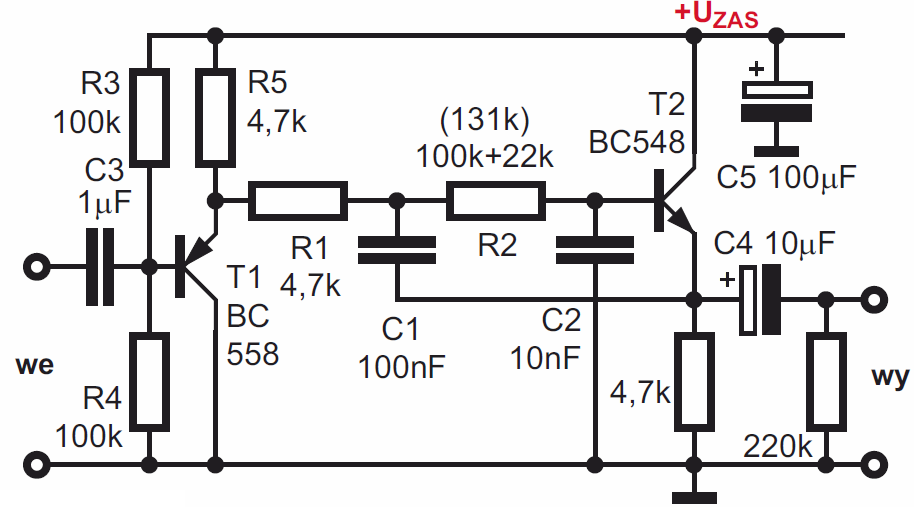
Rysunek 14 i fotografia 15 pokazują tak zwany filtr kroków (górnoprzepustowy o częstotliwości około 100 Hz).
W głosie ludzkim nie ma składowych poniżej 100 Hz – taki filtr jest powszechnie włączany w torach mikrofonowych, gdzie obcina sygnały (zakłócenia) o częstotliwościach poniżej 100 Hz, między innymi odgłosy kroków na scenie – stąd nazwa. W roli R1 wykorzystujemy tu połączone równolegle rezystory 22 kΩ i 100 kΩ. Zwróć uwagę, że w przeciwieństwie do rysunku 10b, mamy tu tylko jeden rezystor R2 (22 kΩ). Aby prawidłowo spolaryzować tranzystory, dodaliśmy (zaznaczony kolorem zielonym) obwód sztucznej masy.
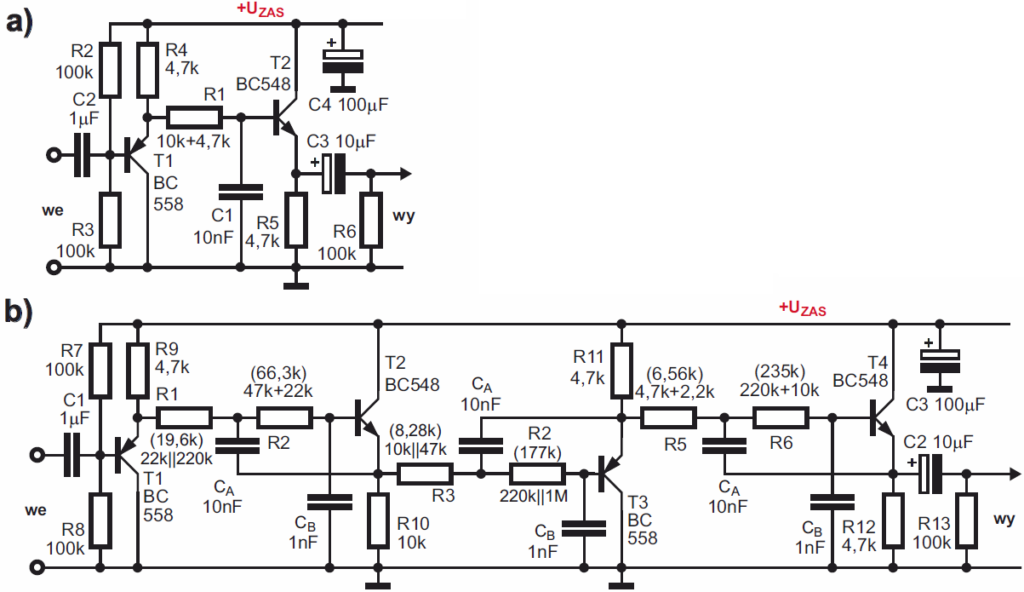
Zachęcam Cię też gorąco do zrealizowania dwóch filtrów dolnoprzepustowych o częstotliwości granicznej 1 kHz według rysunku 16.
Ten prosty to zwykły filtr pierwszego rzędu, ten drugi, rozbudowany, to filtr o charakterystyce Bessela, szóstego rzędu, czyli o dużej stromości charakterystyki amplitudowej, a jednocześnie dobrych parametrach dynamicznych. Potrzebne wartości rezystancji zestawiamy przez łączenie równoległe lub szeregowe dwóch rezystorów, natomiast w nawiasach podane są optymalne wartości rezystancji. Fotografia 17 pokazuje realizację tego filtru. Jeżeli masz kabelki z odpowiednimi wtyczkami (minijack, RCA-chinch), możesz zbudować i włączyć najpierw jeden, potem drugi filtr pomiędzy odtwarzacz CD/DVD lub odtwarzacz MP3 i wejście AUX wzmacniacza mocy domowego zestawu audio. Wtedy na słuch sprawdzisz, na ile skutecznie w obu filtrach obcinane są wyższe częstotliwości.
Jeśli chcesz, możesz zmieniać częstotliwość graniczną tego filtru, wymieniając wartości jednakowych par kondensatorów CA, CB, gdzie CA/CB=10.
Analogicznie mógłbyś zbudować skuteczny filtr górnoprzepustowy, na przykład według rysunku 18.
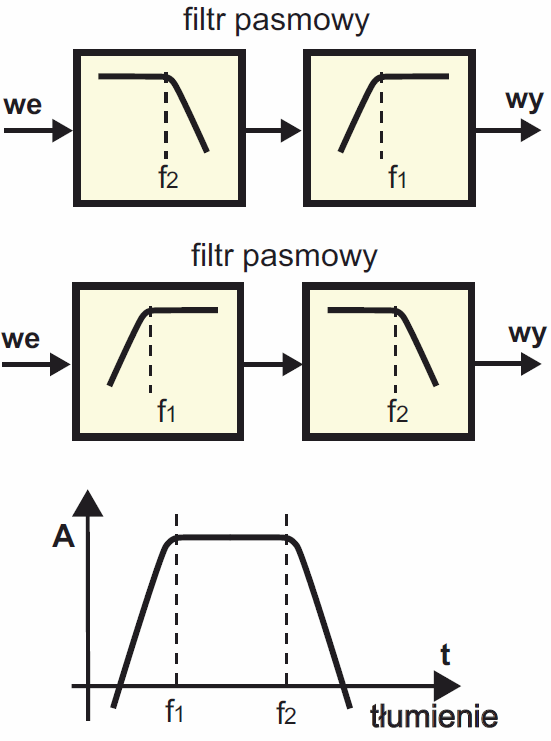
Trzeba też wiedzieć, że złożenie odpowiednio dobranego filtru dolno- i górnoprzepustowego pozwala zbudować filtr pasmowy według idei z rysunku 19. Takie rozwiązanie wykorzystaliśmy w układzie tytułowej iluminofonii. Ale gdyby był potrzebny skuteczniejszy filtr, o znacznie ostrzejszych zboczach, można by go zbudować, łącząc filtry według rysunków 16b i 18. Tylko elementy należałoby dobrać tak, żeby filtr zamiast charakterystyki Bessela, odpowiedniej dla toru audio, miał charakterystykę Czebyszewa, która zapewnia lepsze tłumienie sygnałów spoza pasma przepustowego.
Projektowanie filtrów o zadanych parametrach to niełatwe zadanie. Praktykom, którzy potrzebują jedynie nieskomplikowanych filtrów, polecam moją książkę Wzmacniacze operacyjne, wydaną przez BTC.
Tam, w rozdziale 4 są zawarte praktyczne wskazówki, jak dobierać elementy takich i innych filtrów. Dostępne są także różne specjalizowane programy komputerowe do projektowania filtrów (Filter Wizard). Oferują je m.in. znane firmy: Analog Devices, Texas Instruments, National Instruments. Szereg prostych apletów można też znaleźć na różnych stronach internetowych.
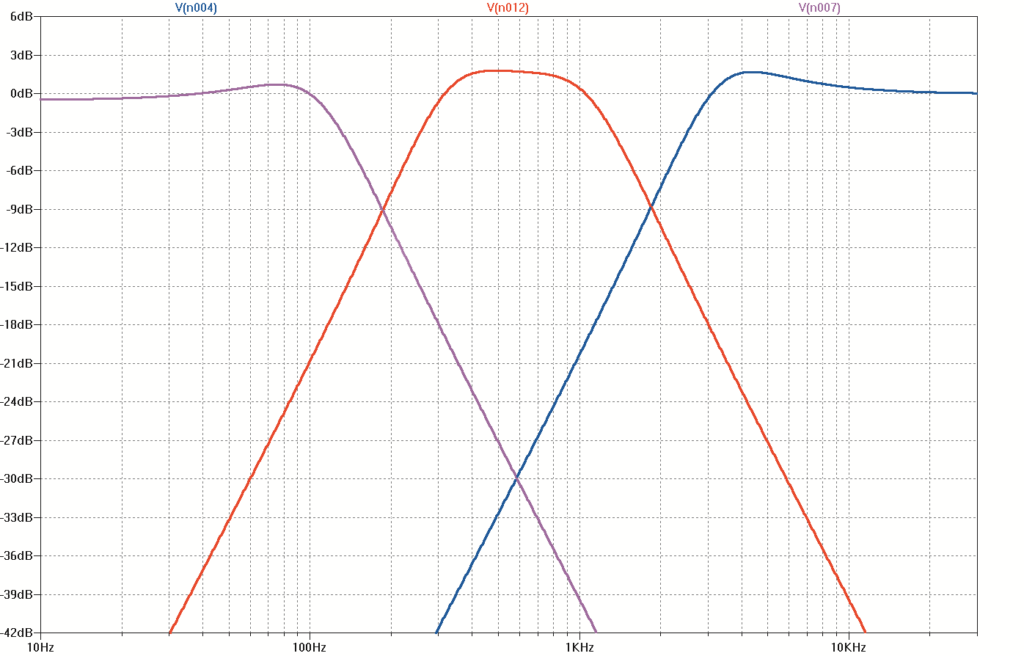
Popularne są również uniwersalne programy do tzw. symulacji. Za pomocą takich programów można w symboliczny sposób (zaskakująco prosty i ciekawy) opisać dowolny układ elektroniczny i zbadać jego różnorodne właściwości. Współczesne programy pozwalają dodatkowo w łatwy sposób narysować schemat i wtedy program ze schematu sam tworzy symboliczny opis układu, potrzebny do symulacji. Niektóre z takich programów są darmowe, jak choćby LTspice z firmy Analog Devices. Znakomicie nadają się także do sprawdzania charakterystyk filtrów. Rysunek 20 pokazuje zrzut ekranu, pokazujący charakterystyki trzech filtrów z projektu wstępnego z rysunków A, B, C.
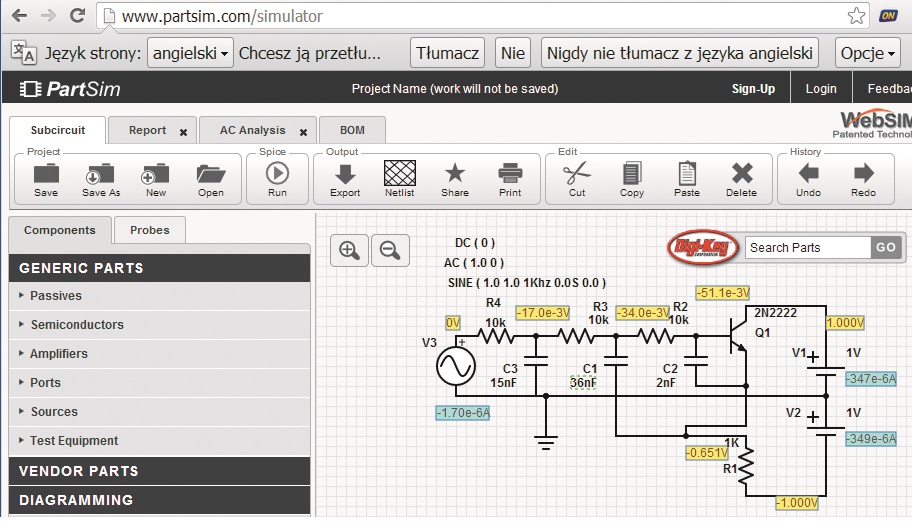
Programy symulacyjne dostępne są też online, jak choćby www.circuitlab.com czy nieistniejący już www.partsim.com – rysunek 21 to zrzut ekranu z symulacji filtru dolnoprzepustowego trzeciego rzędu z nie istniejącej już strony www.partsim.com.
Rezonans. Trzeba też wiedzieć, że zaskakujący efekt daje połączenie cewki i kondensatora i to nie tylko z uwagi na zmiany wartości reaktancji XL i XC, ale głównie z uwagi na przesunięcie fazowe między prądem i napięciem. Otrzymujemy wtedy obwód LC, w którym występuje tzw. rezonans.
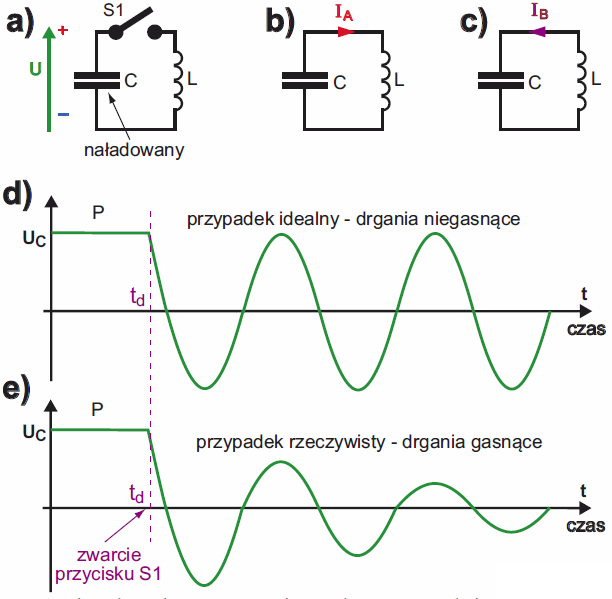
Zjawisko rezonansu związane jest z faktem, że i kondensator, i cewka mogą magazynować energię. A rezonans w sumie polega na tym, że cewka i kondensator na przemian wymieniają się zgromadzoną energią. W idealnym przypadku, w układzie z rysunku 22a, po jednorazowym naładowaniu kondensatora i po zwarciu styku S1 prąd popłynie z naładowanego kondensatora do „pustej” cewki, jak pokazuje rysunek 22b. Cewka najpierw przejmie całą energię, a potem zacznie tę energię oddawać z powrotem do kondensatora, co zilustrowane jest w uproszczeniu na rysunku 22c. Kondensator odzyska całą energię, a potem cykl będzie się powtarzał. Co ciekawe, dziwne i bardzo ważne, w idealnym przypadku energia krążyłaby w nieskończoność między kondensatorem i cewką, a zupełnie nieoczekiwanie napięcie (i prąd) miałyby kształt sinusoidalny, jak pokazuje rysunek 22d. Co jeszcze dziwniejsze, przy jednokrotnym (impulsowym) pobudzeniu, w obwodzie rezonansowym pojawiają się drgania sinusoidalne. I jest to kolejny argument, że właśnie przebieg sinusoidalny jest w pewnym sensie pierwotny, podstawowy
Częstotliwość tego przebiegu, czyli liczba drgań na sekundę, jest wyznaczona przez indukcyjność cewki i pojemność kondensatora według wzoru:
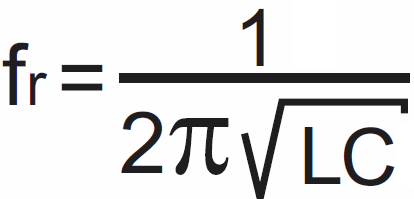
Częstotliwość rezonansu własnego f jest wyrażona w hercach (Hz), gdy indukcyjność L podamy w henrach (H), a pojemność C w faradach (F). Przy częstotliwości rezonansowej reaktancja pojemnościowa XC jest równa indukcyjnej XL. Ze wzrostem częstotliwości reaktancja XL rośnie, a XC maleje, jak pokazuje to w skali logarytmicznej rysunek 23a.
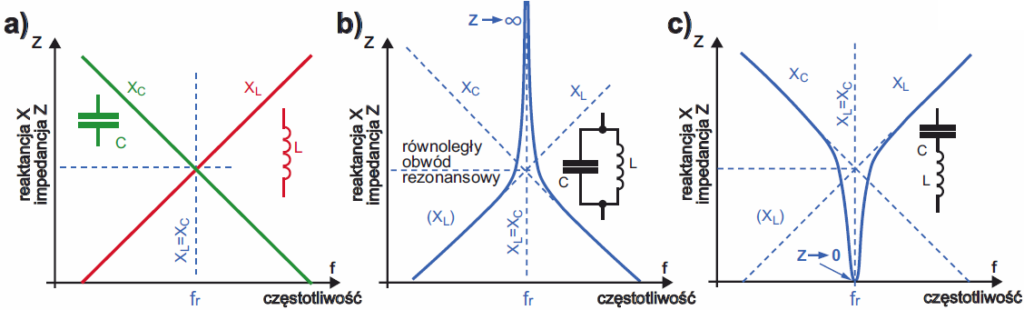
Rysunek 23
Początkujących zaskakuje i dziwi fakt, że przy częstotliwości rezonansowej fr, gdy XL = XC przy równoległym połączeniu elementów LC (czyli w równoległym obwodzie rezonansowym), wypadkowa oporność – impedancja Z staje się… nieskończenie wielka. Ilustruje to rysunek 23b. Natomiast w szeregowym obwodzie LC przy częstotliwości rezonansowej oporność wypadkowa – impedancja staje się… równa zeru, co ilustruje rysunek 23c. Tak byłoby w przypadku idealnych elementów LC.
Zauważ, że taką samą częstotliwość rezonansową fr można uzyskać z cewką o dużej wartości L i kondensatorem o małej wartości C. Albo odwrotnie – taką samą częstotliwość dadzą mała indukcyjność L i duża pojemność C. Byle tylko iloczyn LC był jednakowy. Takie obwody będą się jednak różnić wartością reaktancji charakterystycznej w stanie rezonansu:
XC = 1/2πfC = 2πfL = XL. Wartość liczbową tej tzw. oporności charakterystycznej, inaczej rezystancji charakterystycznej, można obliczyć prościej – jest ona równa: √L/C.
Ale w rzeczywistym obwodzie rezonansowym mamy do czynienia z jeszcze inną rezystancją. Otóż w realnych układach występują rezystancje (drutu cewki, przewodów) oraz dodatkowe straty, więc w każdym cyklu drgań część energii zamienia się na ciepło i jest tracona. Otrzymujemy przebieg sinusoidalny gasnący, jak pokazuje rysunek 22e. Zależnie od tego jak duże są straty energii w rezystancjach i jak szybko gasną drgania,mówimy, że cewka i obwód rezonansowy mają mniejszą lub większą dobroć (oznaczaną Q). Dobroć pokazuje, ile razy rezystancja charakterystyczna jest większa od rezystancji strat.
W praktyce w obwodach LC zawsze występują straty, więc rezystancja rzeczywistego równoległego obwodu (rysunek 22b) jest wielokrotnie większa niż oporność charakterystyczna, ale nie jest nieskończenie wielka. Podobnie w szeregowym obwodzie (rysunek 22c) podczas rezonansu oporność nie staje się równa zeru, tylko ma jakąś niewielką wartość (zwykle nieco większą od rezystancji uzwojenia użytej cewki).
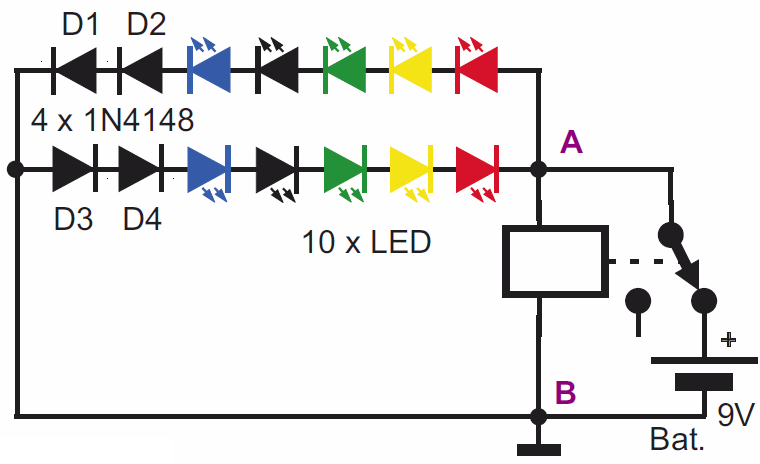
Dziwne zjawisko można zauważyć w prościutkim układzie, który badaliśmy w ramach wykładu 6. Mianowicie możesz jeszcze raz wykonać generator na przekaźniku i dołączyć równolegle do cewki dwa jednakowe łańcuchy LED, włączone przeciwsobnie według rysunku 24 i fotografii 25.
Każdy łańcuch zawiera 5 diod LED i dwie zwykłe diody 1N4148. Sprawdziłem, że taki łańcuch zaczyna leciutko świecić przy napięciu 10,5 V. My zasilamy układ z baterii 9-woltowej. W spoczynku żaden z dwóch łańcuchów LED nie ma prawa świecić. W wykładzie 6 dowiedzieliśmy się, że w chwili przerywania obwodu cewka, która nie lubi zmian prądu, wytwarza ujemne napięcie samoindukcji i prąd płynie przez „dolny” łańcuch diod od punktu B do punktu A, które świecą dość jasno. Jednak podczas działania układu leciutko świeci także „górny” łańcuch, to znaczy, że w pewnych chwilach prąd płynie od punktu A do B, a to znaczy, że w pewnych chwilach w punkcie A występuje napięcie dodatnie względem masy o wartości ponad 10,5 V. Możesz się o tym przekonać, realizując taki układ w praktyce.
Za przyczynę można uznać rezonans, choć w układzie nie ma kondensatora, niemniej są, niezaznaczone na schemacie, wszechobecne małe pojemności montażowe i tak zwana pojemność własna cewki.
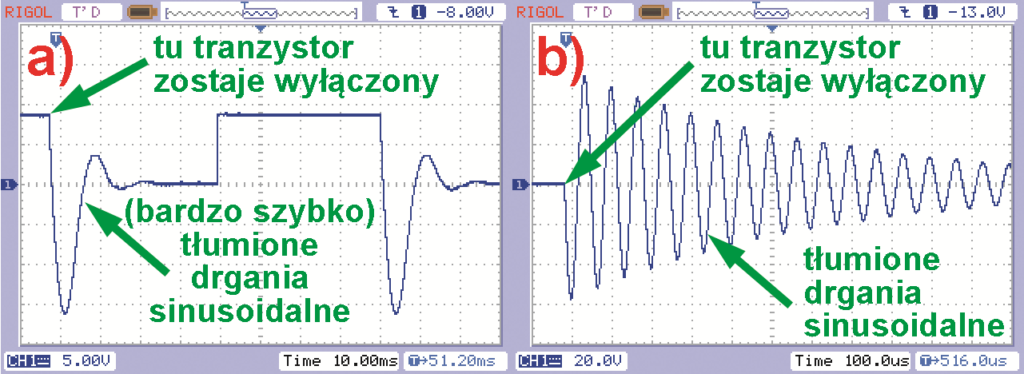
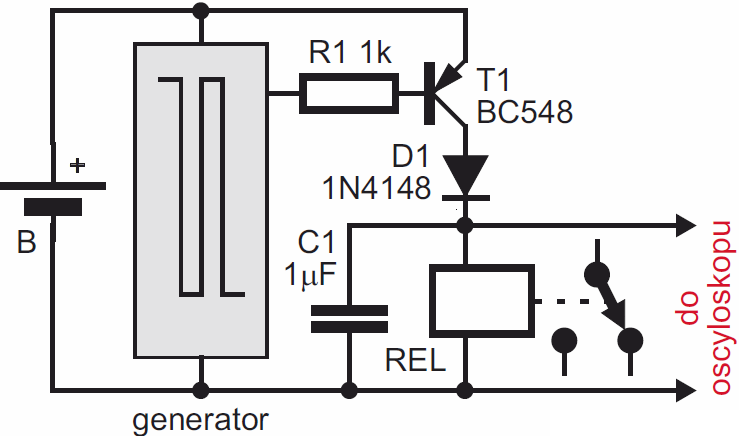
Jedyna nasza cewka (przekaźnika) ma dużą rezystancję i gaśnięcie drgań jest dużo szybsze niż na rysunku 22e. Rysunek 26a to zrzut z ekranu oscyloskopu, pokazujący drgania (bardzo szybko) gasnące, występujące na obwodzie rezonansowym złożonym z kondensatora 1 uF i cewki naszego przekaźnika w układzie z rysunku 27.
Drgania pojawiają się w chwili, gdy tranzystor T1 zostaje zatkany i przez cewkę przekaźnika przestaje płynąć prąd. Wcześniej mówiliśmy, że cewka wytwarza pojedynczy impuls napięcia samoindukcji. W przypadku obwodu rezonansowego powstają drgania gasnące. W tym przypadku drgania gasną bardzo szybko właśnie z uwagi na duże straty energii w rezystancji cewki przekaźnika. Rysunek 26b pokazuje gasnące drgania rezonansowe w obwodzie z inną cewką o znacznie lepszych parametrach (o mniejszej rezystancji, czyli o większej dobroci Q).
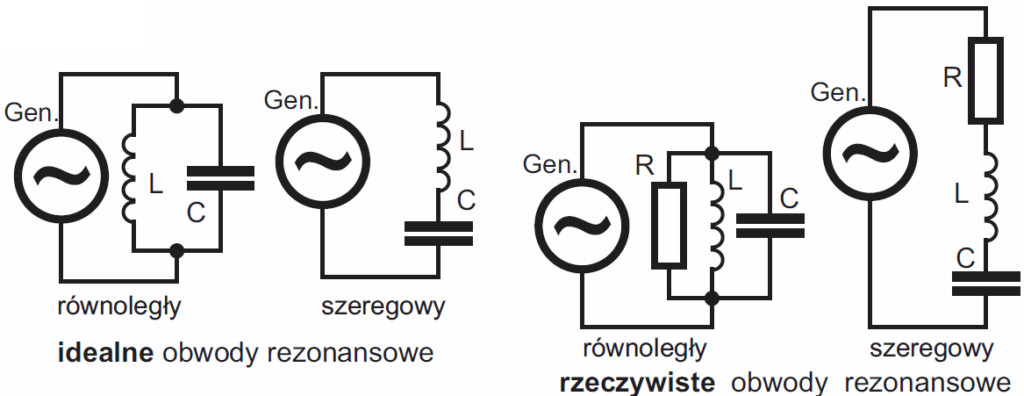
W podręcznikach szkolnych analizuje się obwody rezonansowe równoległe i szeregowe – rysunek 28.
Co ciekawe, obwód rezonansowy „lubi” przebiegi o częstotliwościach zbliżonych do częstotliwości rezonansu własnego:
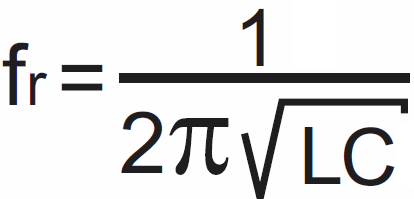
Tym bardziej lubi, fachowo: jest bardziej selektywny, im mniejsze są straty w rezystancjach, czyli czym większa jest dobroć Q.
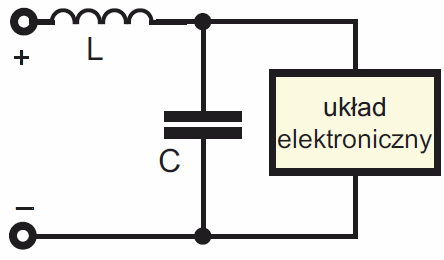
Obwody rezonansowe były i nadal są wykorzystywane w filtrach, na przykład we wszelkich urządzeniach radiowych. Ale trzeba pamiętać, że wszędzie tam, gdzie występuje indukcyjność i pojemność,mamy obwód rezonansowy o lepszej lub gorszej dobroci. Tak jest i w obwodzie filtracji zasilania według rysunku 5b z wykładu 8. Aby przy stosowaniu dławika według rysunku 29 uzyskać dobrą filtrację, a nie tłumione sinusoidy z rysunku 22e, należy prawidłowo dobrać elementy, zastosować dławik o małej dobroci i być może celowo dodać w szereg z kondensatorem C niewielki rezystor
Elementy filtru nieprawidłowo dobrane, „zbyt dobre”, mogą wręcz pogorszyć sytuację, powodując nadmiernie duże drgania rezonansowe. Warto też wiedzieć, że każdy kawałek drutu i każda ścieżka na płytce ma jakąś maleńką indukcyjność i też jest maleńką cewką, więc we wszystkich układach mamy też mnóstwo niepożądanych obwodów rezonansowych – na szczęście przy maleńkich wartościach indukcyjności i pojemności pasożytniczych, ich częstotliwości rezonansowe są bardzo duże, rzędu nawet miliardów herców, czyli gigaherców i nie wpływają na działanie ogromnej większości układów.
Są za to wyzwaniem dla konstruktorów szybkich układów.
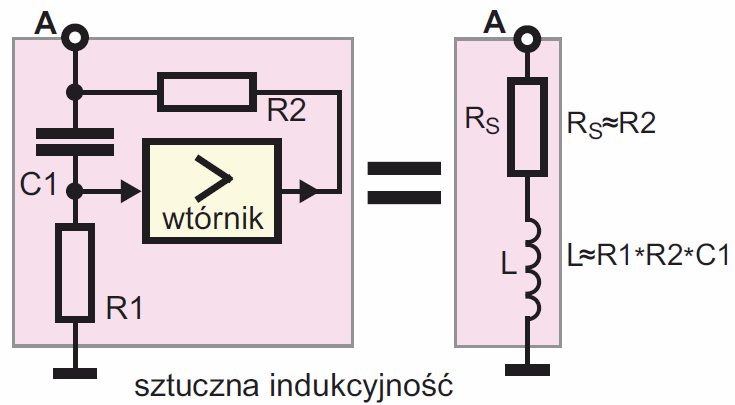
Cewki od dawna nie były lubiane przez hobbystów. Co ciekawe, można w dość proste sposoby zrealizować układ elektroniczny, który pod pewnymi względami zachowuje się jak cewka. Prosty sposób masz na rysunku 30. Taki układ, w przeciwieństwie do cewki, nie magazynuje energii w polu magnetycznym, jednak jeśli chodzi o przeciwstawianie się zmianom prądu i przesunięcie prądu względem napięcia – zachowuje się jak cewka. Ściślej biorąc, jak cewka o rezystancji szeregowej równej R2.
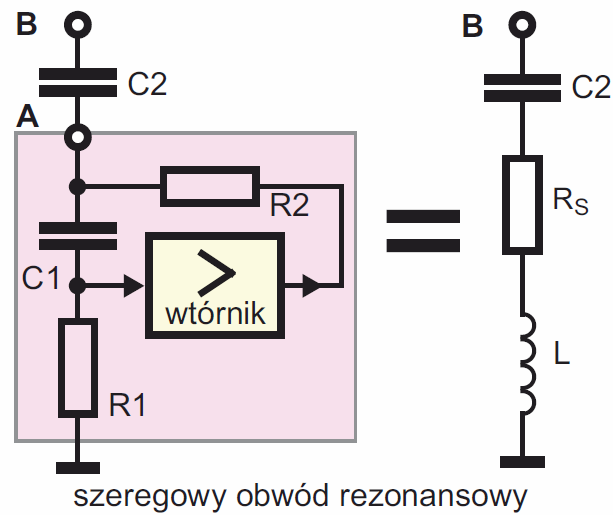
Taka sztuczna indukcyjność pozwala stworzyć obwód rezonansowy. Dołączając kondensator C2 według rysunku 31, tworzymy szeregowy obwód rezonansowy.
Takie obwody rezonansowe są bardzo często stosowane w tzw. korektorach graficznych, zwanych equalizerami.
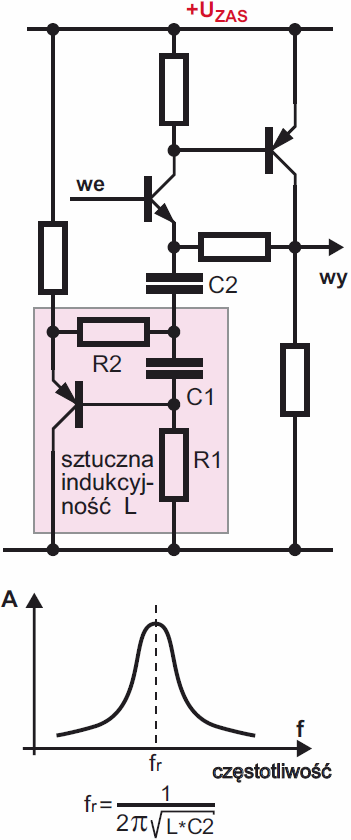
Moglibyśmy wykorzystać taki obwód rezonansowy np. we wzmacniaczu według rysunku 32, uzyskując filtr pasmowy – selektywny.
Jednak właściwości takiego filtru nie są optymalne. Filtry pasmowe realizujemy inaczej. Do filtrów wrócimy jeszcze w jednym z następnych wykładów.
Piotr Górecki