Poznajemy tranzystory – część 9

Niniejszy odcinek zawiera dalsze informacje na temat odprowadzania ciepła i rozkładu temperatur w pracujących tranzystorach mocy. Interesujący prosty sposób oszacowania rezystancji termicznej radiatora „metodą kropelki” pozwoli praktycznie dobierać radiatory w konkretnych zastosowaniach.

Dla utrwalenia wiadomości podanych w poprzednich odcinkach koniecznie wykonaj na początek kilka kolejnych ćwiczeń teoretycznych.

Na rysunku 1 podałem ci trzy podobne sytuacje. Układ jest ten sam (rysunek 1a), taki sam jest radiator i ta sama moc tracona (28 W). W układzie możesz zastosować trzy różne tranzystory mocy, wszystkie w obudowie TO−220 i wartościach Rthjc wziętych z katalogu: odpowiednio 0,92K/W; 1,67K/W oraz 3,1K/W. Oblicz, jakie będą temperatury złącza przy zastosowaniu poszczególnych tranzystorów. Przyjmij Rthcr = 0,2K/W. Temperaturę otoczenia przyjmij równą +40°C.

Tj = Ta+[(Rthra+Rthcr+Rthjc) × Ptot]

b) Tj = 40°+[(1K/W+0,2K/W+0,92K/W) × 28 W] = 99,36°C

c) Tj = 40°+[(1K/W+0,2K/W+1,67K/W) × 28 W] = 120,36°C

d) Tj = 40°+[(1K/W+0,2K/W+3,1K/W) × 28 W] = 160,40°C

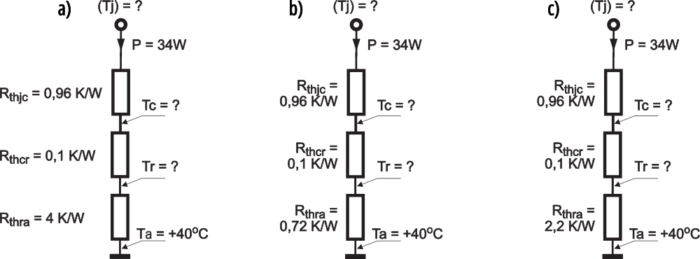
A teraz rysunek 2. Mając dane rezystancje termiczne i wiedząc, jaką moc musisz rozproszyć, oblicz rozkład temperatur w poszczególnych punktach.

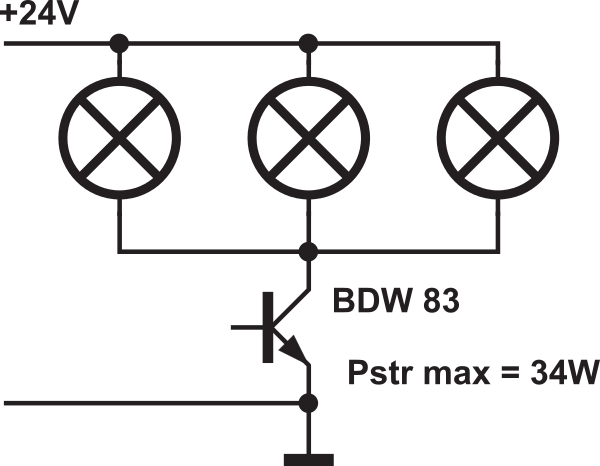
Na rysunku 2 zaznaczyłem ci niektóre wartości. Wydawałoby się, że znając moc żarówek i ich napięcie pracy można obliczyć ich rezystancję, ewentualnie zmierzyć ją omomierzem i podstawić do wcześniej podanych wzorów na moc strat dla najgorszego przypadku. Niestety, dla żarówek nie można w prosty sposób obliczyć mocy strat dla najgorszego przypadku, tak jak liczyliśmy wcześniej z pomocą prostych wzorów dla obciążenia rezystorowego. Powód jest prosty: rezystancja żarówek nie jest stała, tylko bardzo silnie i nieliniowo zmienia się wraz ze wzrostem prądu. Przykładowo żarówka samochodowa 12 V 21 W przy napięciu nominalnym ma rezystancję około 6,8 Ω, natomiast przy bardzo małych napięciach i prądach zimne włókno ma rezystancję około 0,5Ω. Dla żarówki 12 V 10 W rezystancja „gorąca” i „zimna” wynoszą odpowiednio: 14,4 Ω i 1,2 Ω. Dla żarówki 12 V 5 W: 29 Ω i 2,7 Ω, dla żarówki 24 V 21 W: 27,5 Ω i 1,8 Ω. Jaką rezystancję należałoby podstawić do wzoru? Ponieważ rezystancja żarówki tak silnie zależy od temperatury, wzory podane w poprzednich odcinkach nie mogą być zastosowane. Dlatego na rysunku 2 podana jest moc strat wydzielająca się w tranzystorze w najgorszych warunkach (34 W). Już na pierwszy rzut oka widać, że z tranzystorem BDW83 (Ptot=130 W, Tjmax=+150°C, Rthjc=0,96K/W) powinieneś rozproszyć podaną moc 34 W, bo katalogowa moc strat P_tot wynosi aż 130 W. Słusznie!

Przeprowadź obliczenia dla sytuacji z rysunku 2 i trzech różnych radiatorów. Potem wskaż na rysunkach 3a, 3b i 3c temperatury w poszczególnych punktach.

Tj = Ta+[(Rthra+Rthcr+Rthjc) × Ptot]
Tc = Ta+[(Rthra+Rthcr) × Ptot]
Tr = Ta+(Rthra × Ptot)
a)
Tj = 40°+[(4K/W+0,1K/W+0,96K/W) × 34 W] = 212,04°C
Tc = 40°+[(4K/W+0,1K/W) × 34 W] = 179,40°C
Tr = 40°+(4K/W × 34 W) = 176°C
b)
Tj = 40°+[(0,72K/W+0,1K/W+0,96K/W) × 34 W] = 100,52°C
Tc = 40°+[(0,72K/W+0,1K/W) × 34 W] = 67,88°C
Tr = 40°+(0,72K/W × 34 W) = 64,48°C
c)
Tj = 40°+[(2,2K/W+0,1K/W+0,96K/W) × 34 W] = 150,84°C
Tc = 40°+[(2,2K/W+0,1K/W) × 34 W] = 118,20°C
Tr = 40°+(2,2K/W × 34 W) = 114,80°C

Przeanalizuj uzyskane wyniki. Przy ewidentnie zbyt małym radiatorze (wersja z rysunku 3a) temperatura złącza wyniosłaby aż +212°C. To rzeczywiście dużo. Za dużo! Radiator jest za słaby, zbyt mały.

Na pewno przy ogromnym radiatorze z Rthra = 0,72K/W z rysunku 3b wszystko jest w porządku. Temperatura złącza wynosi +100°C, a radiatora około +65°C.

Ale czy w wersji z rysunku 3c mieścimy się w przepisanych granicach? Temperatura złącza to dopuszczalne +150°C. A temperatura obudowy?

Tak! Będzie wynosić około +120°C! Nawet temperatura radiatora sięgnie niemal +115°C.

Ściślej biorąc, taka temperatura wystąpi tylko w punkcie styku czyli tam, gdzie z pomocą smaru silikonowego lub silikonowej (ale nie mikowej) podkładki przykręcony jest tranzystor. Powierzchnia radiatora będzie mieć trochę niższą temperaturę. O ile niższą? To zależy od wielu czynników i nie jest najważniejsze. Nie musisz się w to wgłębiać. W każdym razie na podstawie rysunków: 3a, 3b i 3c możesz się przekonać, że o ile zastosujesz smar silikonowy, to temperatura metalowej wkładki tranzystora TO−220 (takie przecież stosujemy najczęściej) będzie mniej więcej taka, jak temperatura radiatora w miejscu styku z tranzystorem. Różnica kilku stopni nie ma znaczenia.

Czy jednak temperatura obudowy tranzystora wynosząca +120°C to aby nie za dużo?

Woda wrze w temperaturze +100°C, a w temperaturze +120°C kropelka wody szybciutko wyparowuje z lekkim sykiem. Czy można dopuścić takie warunki i gotować wodę na tranzystorze i radiatorze? Do tej pory być może uważałeś, że jeśli możesz dotknąć palcem do radiatora pracującego tranzystora i się nie oparzysz, to radiator jest właściwy. Jeśli nie możesz go utrzymać, bo parzy – radiator jest za mały.

To nie jest dobry sposób oceny radiatora. Nie bój się wyższych temperatur. Wiesz przecież, że temperatura półprzewodnikowego złącza może wynosić nawet +150°C. Dlatego temperatura obudowy tranzystora równa +120°C generalnie nam nie przeszkadza. Nie bój się więc tych +115°C. Oczywiście tak rozgrzanego radiatora nie możesz wystawić na zewnątrz obudowy, bo rzeczywiście ktoś mógłby się poparzyć. Ale jeśli radiator o tej temperaturze jest umieszczony wewnątrz obudowy, to nie ma problemu.

A teraz słówko na marginesie. Być może podziwiałeś potężne, czernione radiatory w niektórych wzmacniaczach mocy. Przykładowo niektóre starsze krajowe wzmacniacze o mocach wyjściowych rzędu 2 x 15…2 x 50 W były wyposażane w takie potężne radiatory, wystające z tylnej ścianki obudowy. Wielkość tych radiatorów może sugerować, że do rozproszenia kilkudziesięciu watów mocy strat potrzebne są koszmarnie wielkie radiatory. Wcale tak nie jest! Wielkość wspomnianych radiatorów wynikała z tego, że były wystawione na zewnątrz i obowiązujące przepisy żądały, by temperatura ich powierzchni nie przekroczyła wyznaczonej granicy. Nie daj się więc zasugerować wielkością radiatorów w takich wzmacniaczach.

Teraz wracamy do głównego wątku. Co wynika z rysunków: 3a, 3b i 3c?

Przy nowoczesnych tranzystorach w obudowach TO− 220 i mocach traconych do 20…30 W możesz przyjąć, że jeśli temperatura metalowej wkładki tranzystora (ściślej styku tranzystora z radiatorem) nie przekroczy +120°C, to tranzystor nie będzie przegrzany. Tylko jak określić tę temperaturę?

Wykorzystaj praktycznie podane informacje. Umieść kropelkę wody na metalowej wkładce tranzystora TO−220, włącz układ i czekaj. Jeśli po ponad minucie pracy układu w pewnym momencie w kropelce wody pojawią się bąbelki pary, kropelka zacznie wrzeć i wyparuje, temperatura obudowy przekroczyła +100°C. Nie wpadaj w panikę! Jeśli teraz umieścisz następną kropelkę wody na wkładce, a ta wyparuje po kilku sekundach, to temperatura wkładki wynosi +100…+110°C. To naprawdę jest dopuszczalna sytuacja. Pamiętaj, że nie jesteś kucharzem, tylko elektronikiem.

Jeśli przy takim eksperymencie pierwsza kropelka wody nie chce wyparować w towarzystwie bąbelków pary i niknie powoli w ciągu kilku minut lub więcej to temperatura obudowy jest niższa niż +100°C i radiator jest dobrany z pewnym zapasem. Oczywiście radiator może być przy tym tak gorący, że w nie będziesz mógł go dotknąć.

Jeśli jednak pierwsza kropelka wyparuje w czasie krótszym niż minuta, a następna kropelka wyparuje z sykiem natychmiast po jej umieszczeniu na wkładce, to szybko wyłącz układ – temperatura obudowy przekroczyła +120°C, a temperatura złącza mogła przekroczyć +150°C. Zastosuj większy radiator, bo ten jest za mały dla danej mocy traconej.

Nie polecam ci innych sposobów pomiaru temperatury, bo w domowych warunkach nie zbudujesz sensownego termometru do pomiaru temperatury obudowy tranzystora. Nie próbuj wykorzystywać sondy zawartej w wyposażeniu lepszych multimetrów cyfrowych. Błąd takiego pomiaru byłby zbyt duży. Do prób z tranzystorami w obudowach TO−220 polecam prosty sposób z kropelką wody.

Dlaczego zalecam próby tylko z obudową TO−220 lub podobną większą, np. TO−218 (SOT−93)? Bo masz wtedy bezpośredni dostęp do metalowej wkładki radiatorowej. W przypadku tranzystorów w plastikowej obudowie TO−126 nie masz bezpośredniego dostępu do wkładki radiatorowej, a temperatura plastikowej powierzchni nie pozwala wnioskować o temperaturze złącza. Podobnie jest ze starszymi tranzystorami w metalowej obudowie TO−3. Też nie masz dostępu do płaszczyzny, przez którą jest przekazywane ciepło do radiatora, a temperatura metalowego kapturka zależy od konstrukcji obudowy i nie pozwala wyciągnąć wniosków na temat temperatury złącza.

W każdym razie eksperymenty z tranzystorami w typowej obudowie TO−220 pozwolą ci wstępnie określić parametry radiatorów, które potem będą współpracować z tranzystorami w innych obudowach.

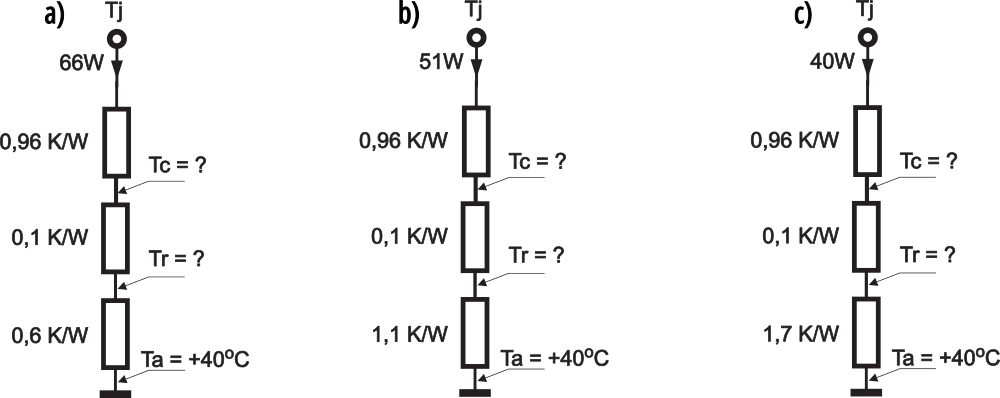
Podałem ci tu z grubsza ogólną zasadę sprawdzenia, czy przy mocach do 20…30 W radiator nie jest za mały. Czy dla większych mocy jest podobnie? Jak rozkładają się temperatury? Jeśli chcesz to sprawdzić, przeprowadź obliczenia i uzupełnij rysunki 4a, 4b i 4c.

Tc = Ta+[(Rthra+Rthcr) × Ptot]
Tr = Ta+(Rthra × Ptot)

a)
Tc = 40°+[(0,6K/W+0,1K/W) × 66 W] = 86,20°C
Tr = 40°+(0,6K/W × 66 W) = 79,60°C
b)
Tc = 40°+[(1,1K/W+0,1K/W) × 51 W] = 101,20°C
Tr = 40°+(1,1K/W × 51 W) = 96,10°C
c)
Tc = 40°+[(1,7K/W+0,1K/W) × 40 W] = 112°C
Tr = 40°+(1,7K/W × 40 W) = 108°C

Sytuacje z rysunków: 4a, 4b i 4c są trochę sztuczne, bo za każdym razem rezystancja radiatora jest tak dobrana, by przy danej mocy strat temperatura złącza nie przekroczyła +150°C. A radiator o rezystancji 0,6K/W to potężny kawał aluminiowej kształtki. W każdym razie sam widzisz, że przy zastosowaniu smaru silikonowego, temperatura obudowy i radiatora różni się niewiele, bo tylko o kilka stopni. Zapamiętaj, że temperatura wkładki radiatorowej jest niższa od temperatury złącza o mniej więcej:

ΔTjc=P×Rthjc

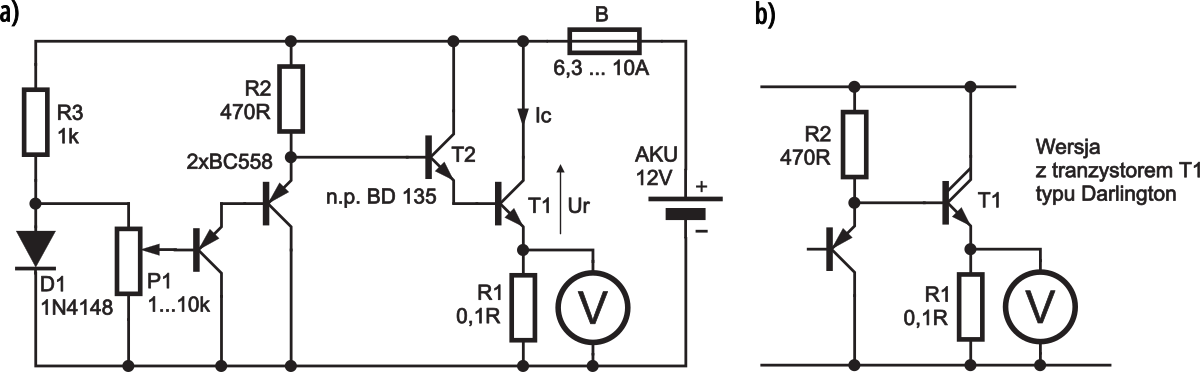
Teraz masz już sporo wiedzy o zależnościach cieplnych. Na razie jest to wiedza czysto teoretyczna. A ty chcesz być praktykiem. Zbuduj więc układ z rysunku 5 lub podobny z tranzystorem T1 w obudowie TO−220 lub TO−218 (SOT−93), o jak największej katalogowej mocy P_tot. Przy przepływie prądu przez tranzystor będzie się w nim wydzielać moc: P=U_T×I_C

Moc tę możesz regulować potencjometrem P1. Przy pierwszym włączeniu zamiast bezpiecznika należy włączyć żarówkę 12 V 10…60 W i ustawić potencjometr P1 na minimum prądu. Dopiero po takim sprawdzeniu można zamienić żarówkę na bezpiecznik.

Podczas późniejszych pomiarów w najprostszym przypadku możesz mierzyć tylko napięcie na szeregowym rezystorze 0,1 Ω. Zakładając, że napięcie akumulatora nie zmienia się i jest równe 12 V (zmierz), moc strat wydzielana w tranzystorze (pomijając straty w rezystorze R1) będzie wynosić:

P [W]=120×U1 [V] gdzie stały współczynnik 120 wynika ze wzoru: I=U_aku/R1, a U1 to wskazanie napięcia na woltomierzu.

Weź kilka radiatorów począwszy od kawałeczka blachy aluminiowej (np. 4 x 4cm) do sporego radiatora z aluminiowego fabrycznego profilu i kolejno sprawdź „metodą kropli”, jaką moc możesz stracić z poszczególnymi radiatorami. Nie przekrocz tylko dopuszczalnego prądu tranzystora mocy. A przy mocy traconej większej niż 30 W nie zapomnij o rezystancji Rthjc, która na przykład dla tranzystorów mocy BD249/250, BDV64/65 wynosi 1K/W, dla BDW93/94 – 1,56K/W, dla BD905…BD912 – 1,4K/W, BD243/244 – 1,9K/W, a dla starych krajowych BD280…286 aż 3,5K/W. Temperatura złącza będzie większa od temperatury obudowy o:

ΔT=P×Rthjc

Jak widzisz jest to bardzo prosty sposób oszacowania rezystancji termicznej radiatora. Pamiętaj jednak, że jest to sposób, powiedzmy„oszczędny”. Może się serdecznie zdziwisz, jak małe będą radiatory potrzebne do rozproszenia mocy 5…10 W przy temperaturze obudowy tranzystora (TO−220) wynoszącej +100…+120°C. W praktyce nie stosuj jednak aż tak małych radiatorów. Pamiętaj, że próby przeprowadzasz na wolnym powietrzu, a potem radiator zamkniesz w obudowie, gdzie będą znacznie gorsze warunki chłodzenia. Poza tym obniżenie temperatury złącza poniżej +150°C jeszcze bardziej zwiększy niezawodność urządzenia. W miarę możliwości stosuj znacznie większy radiator. Ale ze sposobu z kropelką wody nie rezygnuj. Przeprowadź próby, bo pozwoli ci to nabyć doświadczenia, byś potem potrafił dobrać odpowiedni radiator bez żadnych prób i eksperymentów.

Powtórka

Najpierw wydawało ci się, że znając maksymalne napięcie U_CE0 i maksymalny prąd kolektora I_Cmax obliczysz„moc tranzystora” jako U_CE0 x I_cmax.

Okazało się to nieprawdą. Dla każdego tranzystora podaje się w katalogu maksymalną moc strat P_tot, która jest znacznie mniejsza niż iloczyn U_CE0 × I_Cmax.

Potem już byłeś przekonany, że podawana w katalogu moc P_tot to moc, jaką możesz obciążyć tranzystor w każdych warunkach.

Dla maleńkich tranzystorów małej mocy jest to nawet zbliżone do prawdy (o ile otoczenie ma temperaturę nie przekraczającą +30…+40°C), ale dla tranzystorów o mocy strat większej niż 1 W koniecznie trzeba uwzględnić dodatkowe czynniki. Przy bliższym zbadaniu sprawy okazało się, że w grę wchodzi zjawisko tak zwanego drugiego przebicia, które ogranicza zakres pracy przy dużych napięciach kolektora i znacznych prądach.

Przy jeszcze bliższym przyjrzeniu się problemowi najpoważniejszą barierą okazała się maksymalna temperatura złącza i skuteczność odprowadzania ciepła strat ze złącza do otoczenia. Wiążą się one nierozerwalnie z parametrem zwanym rezystancją termiczną.

W przypadku tranzystorów mocy sprawa dodatkowo się skomplikowała, bo całkowita rezystancja termiczna zależy od kilku czynników, a głównie od parametrów zastosowanego radiatora.

Ponieważ katalogowa moc strat P_tot tranzystorów mocy jest mierzona w warunkach laboratoryjnych przy niemal idealnym chłodzeniu, stało się jasne, że w praktycznym układzie w żaden sposób nie uda ci się „wydusić” z tranzystora mocy katalogowej mocy strat, bo potrzebny byłby idealny radiator.

Ostatecznie wyszło na to, że w realnych warunkach pracy tranzystor mocy może być obciążony mocą wynoszącą około połowy podanej w katalogu wartości P_tot, a i to wymaga zastosowania odpowiedniego radiatora.

Teraz już znasz całą niezbędną teorię i potrafisz obliczać także parametry termiczne. Do pełni szczęścia brakuje ci tylko informacji na temat rezystancji termicznej używanych w praktyce radiatorów. Wartości rezystancji termicznej radiatorów znajdziesz w katalogach dobrych firm wysyłkowych. Możesz także z grubsza oszacować rezystancję termiczną mniejszych radiatorów prostą metodą z kropelką wody.

Ciąg dalszy w kolejnej części.

Piotr Górecki