Poznajemy rezystory – część 2
W poprzednim odcinku przedstawiłem ci garść podstawowych informacji o rezystorach. W tym odcinku chciałbym dokończyć rozpoczęty temat o rezystorach. Pora już nauczyć się „odczytywać” wartości rezystorów na podstawie kolorowych kodów paskowych.
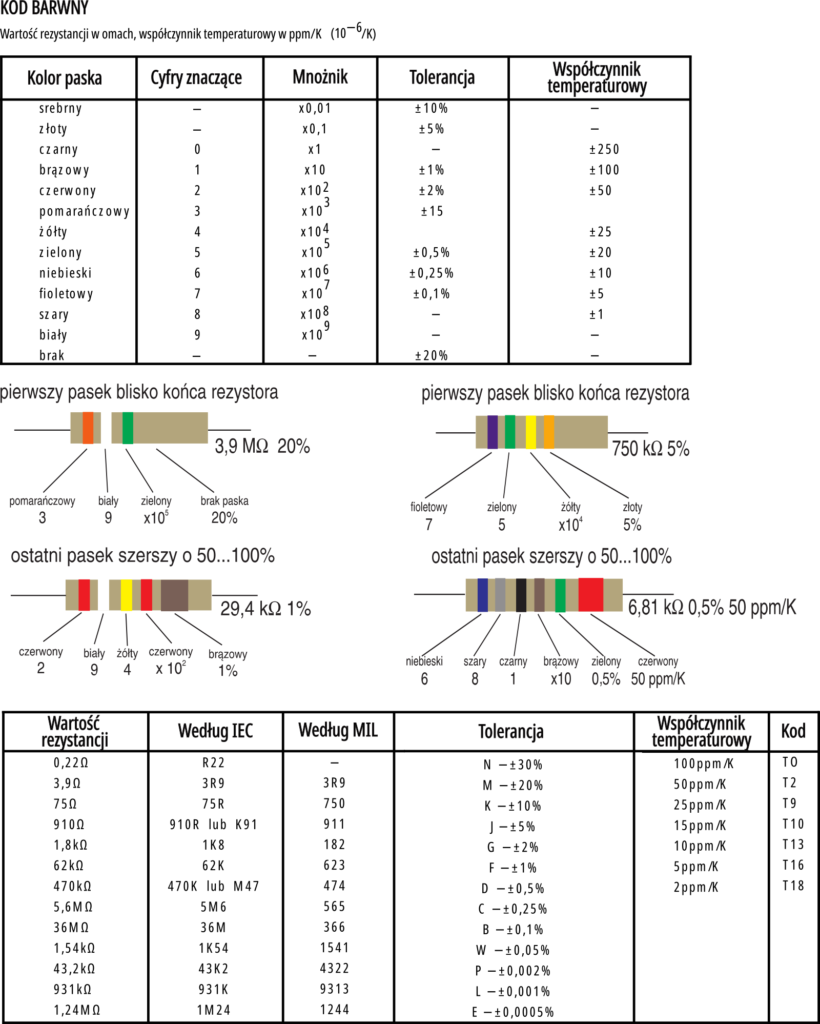
Nauczenie się kolorów wcale nie jest trudne. Naucz się jak wierszyka kolejności kolorów:
czarny − brązowy − czerwony − pomarańczowy − żółty − zielony − niebieski − fioletowy − szary − biały.
Odpowiada to kolejnym cyfrom, uwaga! − od zera do dziewięciu. I teraz znasz już cyfry. Ale to dopiero mniej niż połowa drogi.
Spotyka się też paski srebrne i złote.
Jak wiesz, ktoś kiedyś wykombinował, iż trzeba przyjąć pewne wartości nominalne i produkować elementy według tak przyjętych szeregów. Dlatego nie pytaj nigdzie na przykład o opornik 9,8 kilooma, bo takiego nominału nikt nie produkuje. W artykule znajdziesz tablice szeregów E3 − E192. Liczba obok literki E wskazuje na ilość pozycji dla jednej dekady, czyli na gęstość szeregu. Popularne rezystory, do których jesteś przyzwyczajony, wykonywane są według szeregów E12 i E24. Po analizie tego artykułu i po przeprowadzeniu zaproponowanych eksperymentów zaczniesz cenić te „nieokrągłe” nominały z szeregów: E48, E96 i E192. Nie staraj się nauczyć na pamięć podanych szeregów − pamięć zostaw dla ważniejszych informacji. Z czasem liczby te same „wejdą ci do głowy”. Proponuję ci, żebyś wydrukował kartkę z tymi tablicami i zawsze miał ją „pod ręką”. Dlaczego? Zaraz się przekonasz.
Teoretycznie klucz do zidentyfikowania „kolorowego” opornika jest bardzo prosty. Dla szeregów E12 − E48 wygląda następująco:
pierwszy pasek − pierwsza cyfra znacząca
drugi pasek − druga cyfra znacząca
trzeci pasek − mnożnik (czyli prościej ilość zer)
czwarty pasek − tolerancja.
Pierwszy pasek powinien być umieszczony jak najbliżej brzegu, czyli na metalowym kapturku(obejmie), natomiast ostatni pasek powinien być szerszy od pozostałych.
Przykładowo: czerwony−czerwony−czerwony−złoty oznacza 2,2 kΩ .
Jeśli trzeci pasek jest czarny, do dwóch cyfr znaczących nie dopisuje się żadnych zer. Na przykład oznaczenie: szary−czerwony−czarny daje wartość 82 Ω .
Paski złoty i srebrny nie mogą wystąpić na pierwszych dwóch pozycjach jako cyfry znaczące. Kolor złoty na trzeciej pozycji oznacza mnożnik 0,1. Wtedy kod: zielony−brązowy−złoty daje wartość 5,1 Ω . Pasek srebrny na miejscu mnożnika oznacza 0,01: czerwony−fioletowy−srebrny dawałby więc 0,27 Ω . Jednak rezystory o nominałach poniżej 1 Ω są najczęściej oznaczane cyframi.
Nie wspomnieliśmy dotychczas o ostatnim pasku, określającym tolerancję. Zgodnie z naszym wierszykiem pasek brązowy wskazuje na tolerancję 1%, czerwony − 2%; tolerancja 10% oznaczana jest paskiem srebrnym, a tolerancja 5% − złotym (!), a nie zielonym. Pasek zielony oznacza tolerancję 0,5%, niebieski − 0,25%, fioletowy − 0,1%, szary − 0,05%. Natomiast brak czwartego paska oznacza tolerancję 20%; tak nędznych rezystorów jednak prawie się już dziś nie spotyka.
W praktyce problem polega jednak często na tym, że nie będziesz potrafił stwierdzić „co poeta miał na myśli”, czyli co to miał być za kolor: pomarańczowy, czy żółty; brązowy czy czarny; szary, niebieski, czy może fioletowy? Ponadto, czasem trudno określić, który pasek ma być pierwszy, który ostatni, bo paski naniesione są niedbale, żaden nie jest szerszy od pozostałych i wszystkie umieszczone są mniej więcej na środku rezystora.
I właśnie przy takich wątpliwościach znakomitą pomocą w rozszyfrowaniu będą tabele szeregów i poniższe zasady:
Jeśli są cztery paski (występują dwie cyfry znaczące), to ostatni powinien być złoty albo srebrny, bo popularne rezystory wytwarzane są według szeregów: E12 i E24. Na pewno nie znajdziesz oznaczenia typu: niebieski−szary−czerwony−zielony (6,8 kΩ 0,5%), bo rezystory o tolerancji 0,5% zawsze są wytwarzane według szeregu E192, ewentualnie E96.
Z czterema paskami szybko więc sobie poradzisz. Ale spotkasz rezystory z pięcioma, a nawet sześcioma paskami. Tu zasady są podobne, tyle że występują trzy cyfry znaczące:
pierwszy pasek − pierwsza cyfra znacząca
drugi pasek − druga cyfra znacząca
trzeci pasek − trzecia cyfra znacząca
czwarty pasek − mnożnik
piąty pasek − tolerancja.
ewentualny szósty pasek − współczynnik temperaturowy.
Kolor szóstego paska informuje o temperaturowym współczynniku rezystancji:
brązowy − 100 ppm/K
czerwony − 50 ppm/K
żółty − 25 ppm/K
pomarańczowy − 15 ppm/K
niebieski − 10 ppm/K
fioletowy − 5 ppm/K
Zapamiętaj też raz na zawsze, że to straszne „pi−pi−em” to po prostu skrót „parts per million” czyli swojsko − części na milion:
1 ppm = 1/1000000 = 10−6. Stąd np. 1% = 10000ppm = 104 ppm
100 ppm = 0,01%
Nie licz jednak na to, że na perskim jarmarku kupisz za grosze rezystory o współczynniku temperaturowym mniejszym niż 50 ppm/K (0,005%/K). Jeśli w ogóle spotkasz „sześciopaskowy” rezystor, ostatni pasek będzie najczęściej brązowy albo czerwony.
Przy oznaczeniach pięcio− i sześciopaskowych pomocą w „rozszyfrowaniu” oznaczenia będą tabele ciągów E48 (2%), E96 (1%) i E192 (0,5%). Bardzo rzadko, ale jednak można natknąć się też na dziwolągi; autor ma np. rezystory oznaczone czerwony−czerwony−czarny−czarny−brązowy−czerwony (według podanego klucza 220 Ω 1% 20 ppm/K). Ale według jedno− procentowego szeregu E96 powinno być 221 Ω, nie 220 Ω. Być może jest to wyrób oznakowany kodem Siemensa, niezgodnym z zaleceniami IEC, gdzie trzeci pasek oznacza mnożnik, czwarty − tolerancję (czarny = tolerancja wg specyfikacji klienta) a piąty − trzecią cyfrę znaczącą. Tylko dlaczego pojawił się szósty pasek?
Jak by nie było, nie bój się tych dziwnych pięciopaskowych oznaczeń − jak się pomału przekonasz, rezystory produkowane według tych „gęstych” szeregów są po prostu lepsze.
Podam ci jeszcze na przykładach inne sposoby kodowania parametrów według różnych norm:
| wartość rezystancji | wg IEC | wg MIL |
| 0,15 Ω | R15 | − |
| 1 Ω | 1R0 | 1R0 |
| 39 Ω | 39R | 390 |
| 120 Ω | 120R | 121 |
| 5,6k Ω | 5k6 | 562 |
| 33 kΩ | 33k | 333 |
| 470 kΩ | 470k | 474 |
| 2,7 MΩ | 2M7 | 275 |
| 15 MΩ | 15M | 156 |
Niekiedy w oznaczeniach literkę R pomija się i np. zapis 180 oznacza 180 Ω .
Jeśli w oznaczeniu spotkasz dodatkową literę, to będzie ona oznaczać tolerancję:
N ±30%
M ±20%
K ±10%
J ±5%
H ±2,5%
G ±2%
F ±1%
D ±0,5%
C ±0,2%
B ±0,1%
R1 ±1 Ω (!).
Przykładowo 2k7K = 2,7 kΩ 10%, 4R3J = 4,3 Ω 5%. W niektórych rezystorach również podstawowy kolor obudowy rezystora niesie jakąś informację, ale dla amatora będzie to zbyt trudne do ustalenia, nie są to bowiem zasady znormalizowane i poszczególne firmy ustalają własne reguły.
Teraz już na pewno poradzisz sobie z rozszyfrowaniem rezystancji i tolerancji. Niestety, muszę cię zasmucić − z takiego oznaczenia nie dowiesz się nic na temat dopuszczalnej mocy strat. A można tu się natknąć na duże niespodzianki. Przyzwoity krajowy rezystor MFR o obciążalności 0,25 W ma maksymalne wymiary Ø = 3,4 mm l = 7,2 mm. Tymczasem firma Vitrohm proponuje rezystory tej samej lub lepszej klasy serii GP (1% 50 ppm/K) o obciążalności 0,4 W (typ 490) i wymiarach Ø = 1,6 mm l = 4 mm! Natomiast rezystory GP serii 491 przy wymiarach nadal znacznie mniejszych niż MFR 0,25 W − Ø = 2,5 mm l = 6 mm − mają obciążalność 0,6 W!
Ponieważ większość hobbystów kupuje rezystory pochodzące z różnych, często przypadkowych i niepowtarzalnych źródeł, pożytek z podanych tu cennych informacji z konieczności nie może być pełny. W zasadzie tylko konstruktor−profesjonalista mający dostęp do katalogów konkretnych firm może zamówić rezystory o potrzebnych parametrach − amatorzy muszą sobie radzić nieco inaczej. A przecież co jakiś czas przyjdzie ci wykonać jakiś układ pomiarowy i chciałbyś uzyskać powtarzalne i stabilne parametry. Czy potrafisz odróżnić rezystor węglowy klasy RWW od metalowego MŁT? A jakie parametry mają często spotykane na rynku rezystory produkcji czeskiej albo byłego NRD? Nie masz szans określić tego na podstawie katalogów. Włącz więc wreszcie swą lutownicę. Rezystory masz już przygotowane − do tej próby weź tylko małe rezystory o mniej więcej jednakowej wielkości (popularne ćwiartki i ósemki). Dołączaj teraz po kolei rezystory do miernika cyfrowego, zapisuj rezystancję w stanie zimnym, a potem podgrzewaj każdy opornik mniej więcej w jednakowy sposób. Ja podgrzewałem lutownicą nóżkę rezystora w odległości około 1 mm od korpusu. Zapisz teraz rezystancję każdego opornika w stanie gorącym. Następnie zostaw je w spokoju, aż ostygną do temperatury pokojowej i znów zmierz i zapisz ich rezystancję. Wykonaj to porządnie i dokładnie. Przeanalizuj wyniki. Ja podam ci swoje wnioski, ale ty nie bądź leniwy − wykonaj to ćwiczenie i przekonaj się… jaki złom nagromadziłeś w swych zapasach.
Ja przebadałem w ten sposób ponad 50 rezystorów. Niektóre moje wyniki od najgorszych do najlepszych wyglądają następująco:
Rezystor brązowy−czarny−niebieski−złoty (10 MΩ 5%) niewiadomej produkcji kupiony na perskim. Na zimno − 10,26 MΩ , na gorąco − 6,55 MΩ (!), po ostygnięciu − 10,15 MΩ . Zauważ, że po podgrzaniu symulującym wlutowanie w płytkę rezystancja zmieniła się, bagatela, o 37%! A nominalna tolerancja ma wynosić 5%! Po ostygnięciu rezystancja nie wróciła też do początkowej wartości − „rozjechała się” o ponad 1%. Takiego rezystora nie można użyć do żadnego prawdziwego przyrządu pomiarowego. Ale popatrz dalej:
Rezystor „na oko” MŁT 0,25 W oznaczony 2M7. W stanie gorącym rezystancja spadła z 2,688 MΩ do 2,290 MΩ czyli o 15% − on także nie nadaje się do żadnych precyzyjnych urządzeń.
Podobnie rezystor brązowy−czarny−zielony− złoty (1 MΩ 5%). Przed próbą: 1017,0 kΩ, na gorąco 896 kΩ (−12%), po ostygnięciu 1005,0 kΩ , czyli też „rozjechał się” o ponad 1%. Ale już radziecki rezystor C2−14 o nominale 988 kΩ (szereg E192!) miał wyniki odpowiednio: 987 kΩ; 983 kΩ; 987 kΩ. Podgrzanie zmieniło rezystancję tylko o 0,4%, a po ostygnięciu powrócił on do pierwotnej wartości. Ten rezystor świetnie nadaje się do zastosowania w dokładnym przyrządzie pomiarowym.
Z kolei rezystory niebieski−szary−żółty−złoty (680 kΩ 5%) zmniejszyły swą rezystancję po podgrzaniu o 8…10%. Tej samej klasy oporniki: brązowy−czarny−żółty−złoty (100 kΩ 5%) zmniejszyły rezystancję o 4…6% a po ostygnięciu rezystancja różniła się o 0,2…1% od początkowej. Rezystory MŁT 0,125 W 100 kΩ zmniejszyły rezystancję o 3,3%, ale powróciły do pierwotnej wartości z dokładnością 0,2%. Dla dobrego rezystora MFR 0,125 W rezystancja wynosiła kolejno: 99,74 kΩ ; 100,04 kΩ (+0,3%), 99,82 kΩ (<0,1%). Z tego nominału najlepszy okazał się jednak niepozorny, miniaturowy (Ø = 1,6mm l = 4mm) rezystorek oznaczony brązowy−czarny−żółty−złoty − 100 kΩ 5%, którego rezystancja wyniosła: 100,0 kΩ ; 99,90 kΩ (−0,1%); 99,97 kΩ (0,03%)!
W okolicach 10…20 kΩ sytuacja wyglądała tak:
MFR 0,25 W o nominale 9,09 kΩ: 9,131 kΩ; 9,109 kΩ (−0,24%); 9,131 kΩ (0%!).
Węglowy: brązowy−czarny−pomarańczowy−złoty (10 kΩ 5%): 10,256 kΩ; 9,630 kΩ (−6,1%); 10,280 kΩ (+0,2%!?).
MŁT 18 kΩ 0,25 W: 17,855 kΩ; 18,151 kΩ (+1,6%); 17,855 kΩ.
Podobnie było z opornikami o mniejszej rezystancji. Odchyłki w stanie gorącym nie przekraczały dla rezystorów MFR wartości 1%, dla innych dochodziły do 5%.
Jeszcze raz zachęcam cię, żebyś wykonał takie próby ze swoimi rezystorami. Choć na podstawie takich eksperymentów nie określisz dokładnie temperaturowego współczynnika rezystancji, jednak zorientujesz się, że większość twoich rezystorów zupełnie nie nadaje się do precyzyjnych układów. Nie znaczy to, że są one nieprzydatne − w większości układów mimo wszystko znakomicie spełnią swoją rolę.
Dobieranie lub łączenie popularnych, tanich rezystorów w celu osiągnięcia dokładnie określonych wartości bardzo często zupełnie nie ma sensu. Pamiętaj o tym, że podczas lutowania rezystancja taniego rezystora węglowego może się trwale zmienić o ponad 1%. Także jeśli przepływający prąd podgrzeje rezystor i jego temperatura znacznie się zwiększy, rezystancja może „uciec” nawet poza nominalny zakres tolerancji.
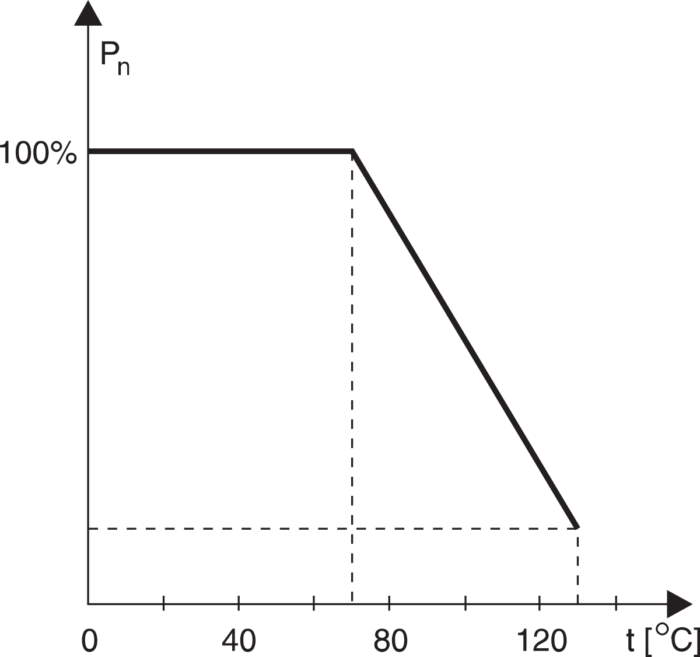
Zwróć jeszcze uwagę na rysunek 1 przedstawiający zależność dopuszczalnej mocy traconej w rezystorach MŁT od temperatury otoczenia. Z rysunku tego wynika, że dopuszczalna temperatura warstwy rezystancyjnej nie może przekraczać +130°C. Dla innych rezystorów maksymalna temperatura warstwy rezystancyjnej może być nieco inna. Dla węglowych: +125°C, dla metalowych MFR i podobnych: +155°C. Ponadto prawie wszystkie rezystory można obciążać mocą znamionową tylko wtedy, jeśli temperatura otoczenia nie przekracza +70°C, ale w praktyce jest to warunek łatwy do spełnienia.
Rozważ teraz następujący przykład: masz zbudować dokładny termometr. W układzie występuje nowoczesny układ scalony − źródło napięcia wzorcowego o stabilności 50 ppm/K (0,005%/K). Napięcie to jest jednak za wysokie i zastosowałeś dzielnik zawierający obok rezystora MFR także rezystor węglowy RWW albo metalowy MŁT, których wartość dokładnie dobrałeś za pomocą cyfrowego multimetru. Jeśli temperatura wewnątrz przyrządu wyniesie, powiedzmy +50°C, a przez rezystory będzie płynął znaczny prąd to może się okazać, że temperatura warstwy czynnej rezystora może wynieść +70…+100°C. Jeśli nawet przed wlutowaniem mierzyłeś rezystor węglowy w temperaturze pokojowej, to w czasie pracy jego rezystancja może zmienić się nawet o 2…4%. Nawet rezystor MFR o współczynniku temperaturowym w granicach ±100 ppm/K może w takich samych warunkach zmienić swą rezystancję o 0,5%. Czy to będzie precyzyjny dzielnik, jeśli jedna z rezystancji zmieni się o kilka procent? Jaka będzie dokładność i stabilność twojego termometru?
Jakie z tego wypływają wnioski?
Dla osiągnięcia wymaganej stałości należy więc stosować sprawdzone dobre rezystory metalowe, i w żadnym wypadku nie obciążać ich pełną mocą znamionową.
Nie wspomniałem ci do tej pory nic o szumach rezystorów – to obszerny temat wymagający kilku artykułów. Powiem ci tylko krótko: tanie „czteropaskowe” oporniki węglowe, a także metalowe typu MŁT i podobne, szumią nawet dziesięciokrotnie więcej niż dobre „pięciopaskowe” rezystory metalowe. Wiem, że będziesz próbował budować różne wzmacniacze akustyczne. A może już próbowałeś i zniechęciłeś się beznadziejnie dużymi szumami? Wiedz, że jedną z przyczyn twojego niepowodzenia mogły być rezystory.
Czy już jesteś przekonany, że w pierwszych stopniach niskoszumnych przedwzmacniaczy powinieneś stosować właśnie te drogie, precyzyjne rezystory metalowe o tolerancji 1% i małym współczynniku temperaturowym? Choć akurat wąska tolerancja i stabilność temperaturowa nie będą najistotniejsze w sprzęcie audio, takie właśnie rezystory powinieneś zastosować ze względu na szumy.
Teraz już chyba zrozumiałeś dlaczego w firmowym sklepie warto zapłacić za dobry metalowy rezystor o tolerancji 1% i stabilności ±50ppm/K dziesięć razy więcej niż za oporniki niewiadomego pochodzenia oferowane „na perskim” w paczkach po sto sztuk.
A teraz weź wszystkie przebadane rezystory i nożem usuń lakier z ich powierzchni. Przypatrz się dobrze warstwie przewodzącej. Jak ukształtowana jest warstwa czynna? Czy widzisz, że ma ona nacięcia w formie spirali? Czy zauważyłeś, że poszczególne rezystory mają różne ilości naciętych „zwojów”? Ile twoich oporników nie ma nacięć, a warstwa czynna jest jednolita? Znalazłeś chociaż jeden?
Dzięki tym zwojom zwiększa się długość ścieżki oporowej i można uzyskać większą rezystancję. Ale zauważ, że rezystory o nominałach poniżej kilooma też mają nacięcia i to czasem w większej ilości niż oporniki kilkudziesięciokiloomowe! Ale nacięcia w kształcie spirali tworzą przecież zwoje cewki − twoje rezystory mają więc pewną indukcyjność. Ponieważ będziesz chciał budować także układy w.cz., nie zapomnij o tym fakcie. Co prawda w układach w.cz. rzadko stosuje się oporniki o dużych rezystancjach (z wieloma naciętymi zwojami), jednak i rezystory o mniejszych nominałach mają pewną szkodliwą indukcyjność (i także pojemność). Do częstotliwości, powiedzmy 10 MHz możesz się tym zupełnie nie przejmować, ale dla częstotliwości rzędu dziesiątek i setek megaherców twoje rezystory będą raczej słabymi cewkami lub kiepskimi obwodami rezonansowymi, a nie rezystorami.
Z tymi spiralnymi nacięciami wiąże się jeszcze jedna historia. Wyglądałoby na to, że rezystor 10 MΩ o obciążalności 0,25 W mógłby pracować w warunkach 1500 V, 150 μA, bo daje to moc 0,225 W. Tak jednak nie jest! Jeśli tak wysokie napięcie rozłoży się na długości ścieżki oporowej, może się zdarzyć, iż napięcie między poszczególnymi zwojami będzie na tyle duże, że nastąpi przebicie między sąsiednimi zwojami. Zagrożenie to związane jest właśnie z obecnością wąskich nacięć międzyzwojowych. Dlatego producenci podają zawsze dopuszczalne napięcie kategorii, które dla rezystorów wielkości „ósemki” (1/8 W) wynosi przeważnie 150…250 V, a dla „ćwiartek” − 200…400 V. Ograniczenia tego nie można lekceważyć. Jeśli więc chcesz stosować zwykłe rezystory w obwodach wysokonapięciowych musisz szeregowo połączyć kilka jednakowych oporników.
Dochodzisz pomału do końca eksperymentów z rezystorami. Powiedziałem ci, że „po drodze” sporo zepsujesz. Weź teraz mocne szczypce i spróbuj przełamać każdy rezystor na połowy. Popatrz, co widzisz na przełomie. Czy wszystkie twoje rezystory mają biały, porcelanowy środek? W takim razie wszystkie twoje oporniki są rezystorami warstwowymi, żaden nie jest rezystorem masowym, zapomnij więc o książkowych klasyfikacjach dzielących oporniki na warstwowe i masowe. Jako masowe wykonywane są, choć i to nie jest regułą, rezystory bezindukcyjne do w.cz. i rezystory wysokonapięciowe.
Jeśli masz jakieś rezystory drutowe (RDC, RDCO itp.) poświęć też po jednym, połam je i zobacz jak są zbudowane. Rezystory drutowe mają zwykle dobre współczynniki temperaturowe i szumowe. Jednak ze względu na swoją budowę najczęściej nie nadają się do układów w.cz.
Do dziś wiele rezystorów najwyższej klasy to rezystory drutowe. Prawdopodobnie jednak nigdy w życiu nie dostaniesz do ręki takiego rezystora o współczynniku temperaturowym np. 2ppm/K. Natomiast spotykane powszechnie rezystory drutowe są rezystorami o większej mocy strat − kilka do kilkudziesięciu watów. Warto wiedzieć, że popularne rezystory RDCO mają niewielki współczynnik temperaturowy ±100−±200 ppm/K w zależności od rezystancji.
No cóż… zakończyłeś zajęcia w swoim małym laboratorium. Czy dowiedziałeś się czegoś nowego? Mam nadzieję, że przeprowadziłeś podane eksperymenty i wiesz już czego możesz spodziewać się po swoich rezystorach.
Nie zapomnij też umieścić w łatwo dostępnym miejscy „ściągawki” z tabelkami i szeregami − zapewniam cię, że często będziesz z niej korzystał.
Piotr Górecki