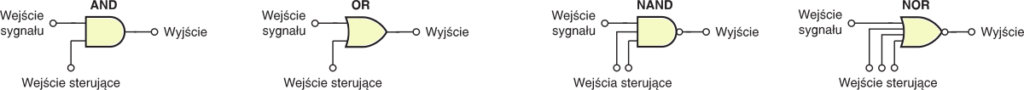Pierwsze kroki w cyfrówce – część 2

W poprzednim odcinku przedstawiłem ci szerokie tło zagadnienia. Dowiedziałeś się, że cała technika cyfrowa w rzeczywistości opiera się na kilku podstawowych cegiełkach, zwanych bramkami. Co ważne, mogłeś sobie uświadomić, że technika cyfrowa nie jest nierozłącznie związana z układami scalonymi − układy logiczne i cyfrowe mogą być realizowane z użyciem na przykład elementów hydraulicznych i pneumatycznych.

W dzisiejszym odcinku nie zaspokoję jeszcze twoich gorących oczekiwań − nie podam ci jeszcze opisu poszczególnych układów scalonych. Przedstawię ci za to bardzo ważne zagadnienia dotyczące bramek. Jeśli nawet znasz już trochę technikę cyfrową, nie lekceważ podanych wskazówek. Jeśli zaczynasz od początku, przeanalizuj podany materiał kilkakrotnie, aby dobrze ci się utrwalił.

Może w pierwszej chwili podane informacje wydadzą ci się niezgodne z tym, czego nauczyłeś się z książek. Tak jednak nie jest − żadnej sprzeczności tu nie ma, ja chcę ci tylko pokazać i zaproponować intuicyjne podejście do układów logicznych. Takie podejście pozwoli ci bez trudu projektować prostsze układy. Zaryzykuję twierdzenie, że „szkolne” podejście, oparte na algebrze Boole’a i licznych wzorach, jest coraz mniej potrzebne w praktyce − skomplikowane układy logiczne realizuje się obecnie z użyciem mikroprocesorów i układów programowalnych PLD, i czarną robotę wykonuje wtedy komputer, a nie człowiek.

Natomiast prostszych układów scalonych, zawierających bramki, nie wolno lekceważyć, bowiem długo jeszcze będą stosowane w urządzeniach elektronicznych.

Przypomnij sobie…

W układach logicznych i cyfrowych mamy do czynienia z dwoma podstawowymi stanami: jest/nie ma, prawda/fałsz, lub inaczej wysoki/niski. Stany te oznaczane są często: 1, 0 albo T, F (True − prawda, False − fałsz).

Nas interesować będą urządzenia elektryczne, w szczególności układy scalone. Układy takie zasilane są napięciem w granicach 2…20 V. Ujemny biegun zasilania jest masą i względem tej masy mierzymy napięcia. Umawiamy się, że obecność napięcia na wejściu lub wyjściu będziemy nazywać stanem wysokim − będziemy go oznaczać literą H (ang. High − wysoki). Brak napięcia to stan niski − oznaczymy go zgodnie z podaną konwencją, literą L (Low − niski). Przyzwyczaj się do oznaczania stanów logicznych literami L i H. Jest to praktyczne, ponieważ w przyszłości unikniesz wielu pomyłek. Nie przyzwyczajaj się do oznaczeń 1, 0, bowiem jedynka logiczna może ci się potem mylić z liczbą 1 lub dużą literą I, a zero logiczne co jakiś czas pomyli się z dużą literą O (a pamiętaj, że litery: I, O są używane do opisywania wejść i wyjść układów cyfrowych).

Dlatego zachęcam cię do używania sformułowania typu: „na wyjściu bramki U1A występuje stan wysoki” (lub krótko stan H), zamiast: „na wyjściu bramki U1A występuje jedynka”. Naprawdę zaoszczędzi to pomyłek i nieporozumień.

Mamy trzy podstawowe bramki: NOT, AND i OR. Są to powszechnie używane określenia angielskie oznaczające po polsku: NIE, I, LUB. W ramach niniejszego cyklu będziemy używać terminów angielskich zrozumiałych na całym świecie. Cała źródłowa literatura elektroniczna ukazuje się po angielsku i chyba nie ma większego sensu trzymać się lokalnych nazw i określeń.

Zapewne w mądrych książkach o technice cyfrowej spotkałeś tak zwane tabele prawdy. Nie próbuj uczyć się tych tablic na pamięć, tylko spróbuj zrozumieć zasady. Wprawdzie tabele te rzetelnie opisują zachowanie układów logicznych, ale ja na początek zalecałbym ci raczej podejście intuicyjne. Poczuj więc cyfrowego bluesa.

A jeśli chcesz, to w przyszłości korzystając z książek, zajmiesz się tablicami prawdy i algebrą Boole’a. Niekiedy bywa to pomocne przy realizacji bardziej skomplikowanych układów.

NOT, AND, OR

W naszych rozważaniach przyjmujemy, że stan wysoki to napięcie równe lub bliskie dodatniemu napięciu zasilającemu, natomiast stan niski to napięcie równe lub bliskie potencjałowi masy. Nie rozpatrujemy żadnych stanów pośrednich − interesuje nas tylko czy jest napięcie, czy go nie ma.

Najprostsza bramka NOT, zwana też negatorem lub inwerterem, realizuje negację − stan na wyjściu jest przeciwny niż stan na wejściu. Jeśli na wejście podamy stan wysoki, na wyjściu pojawi się stan niski, i na odwrót.

Rysunek 1 pokazuje przykładowe sposoby realizacji bramki NOT oraz powszechnie używany symbol tej bramki.

Przy okazji, na rysunku 1 podałem symbol bufora − jest to element, który po prostu powtarza na wyjściu stan z wejścia. Może się zdziwisz i zapytasz: po co? Przekonasz się, że wbrew pozorom jest to bardzo przydatny element.

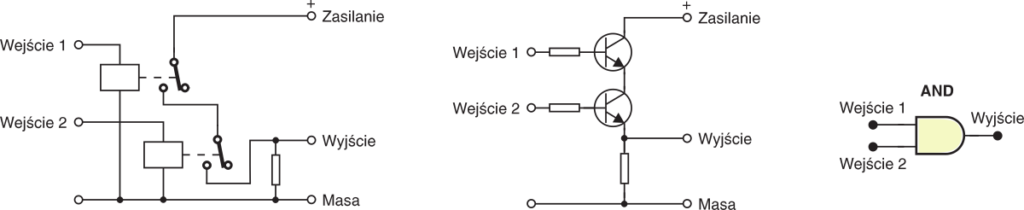
Bramka AND realizuje tzw. iloczyn logiczny − stan na wyjściu bramki AND zmienia się na wysoki dopiero wtedy, gdy na wszystkie wejścia bramki podany jest stan wysoki.

Na rysunku 2 możesz zobaczyć kilka przykładów realizacji bramki AND oraz najczęściej używany symbol tej bramki.

Bramka OR realizuje funkcję tak zwanej sumy logicznej − wystarczy podać stan wysoki na przynajmniej jedno wejście bramki OR, a stan na jej wyjściu zmieni się na wysoki.

Rysunek 3 pokazuje kilka realizacji bramek OR.

W praktyce pojedynczych bramek AND i OR używa się rzadko, można nawet powiedzieć bardzo rzadko. W większości układów budowanych z bramek stosuje się bramki NAND i NOR.

Najpopularniejsze cegiełki: NAND i NOR

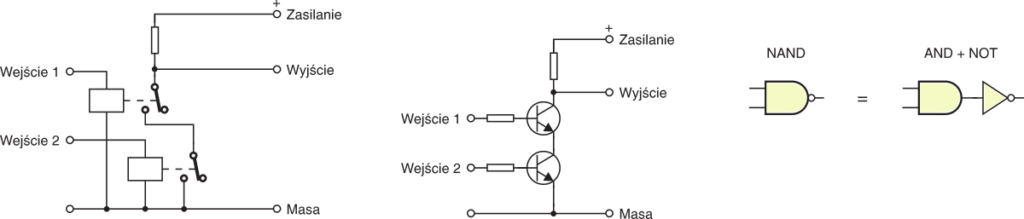
Bramka NAND to jakby połączenie bramek AND i NOT obrazuje to rysunek 4.

Kółeczko na wyjściu świadczy, że mamy do czynienia z negacją. W praktyce bramkę NAND można zrealizować równie prosto lub nawet prościej, niż bramkę AND − porównaj rysunki 2 i 4. To samo dotyczy bramki NOR pokazanej na rysunku 5.

Z rysunku 4 możesz się dowiedzieć, jak pracuje bramka NAND: stan wyjścia zmienia się z wysokiego na niski tylko wtedy, gdy na wszystkich wejściach jest stan wysoki. W bramce NOR stan wyjścia zmienia się z wysokiego na niski, gdy na co najmniej jednym wejściu występuje stan wysoki.

Zauważ, że mówiliśmy tu jakby o stanie spoczynku na wyjściu. Możemy to tak rozumieć. W bramkach AND i OR takim stanem spoczynku na wyjściu jest stan logiczny niski, a w bramkach NAND i NOR − stan wysoki. Milcząco zakładamy też, że stanem spoczynku na wejściach jest stan niski.

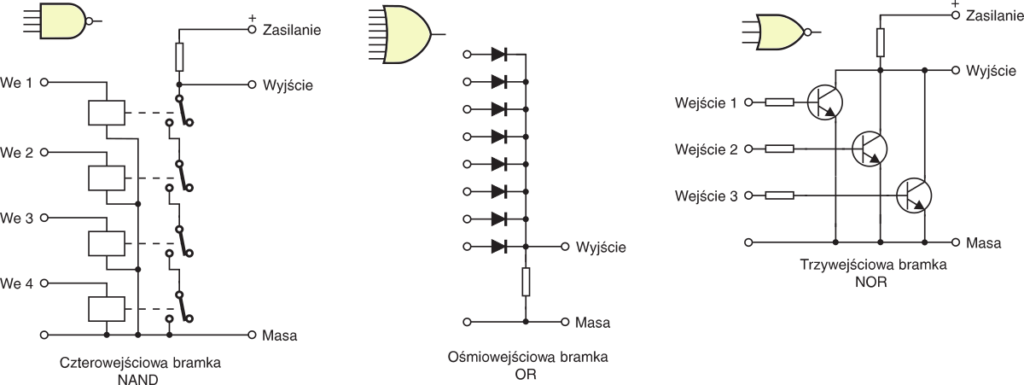
Stan wyjścia zmienia się po spełnieniu warunku:

− dla bramek AND i NAND na wszystkich wejściach musi być stan wysoki, − dla bramek OR i NOR przynajmniej na jednym wejściu musi być stan wysoki. Do tej pory rysowałem ci bramki dwuwejściowe. W praktyce takich bramek używa się najczęściej. Ale istnieją też (w postaci układów scalonych) bramki wielowejściowe − kilka z nich zobaczysz na rysunku 6.

A do czego potrzebne będą ci bramki? W jednym z następnych odcinków podam ci garść wskazówek na temat praktycznego wykorzystania bramek.

Na razie widzisz, że za pomocą bramek OR, NOR możesz sprawdzać, czy na wszystkich wejściach występuje stan niski. Natomiast bramki AND i NAND poinformują cię, czy na wszystkich wejściach występuje stan wysoki.

Ale to za mało. Proponuję ci wyrobienie sobie nawyków myślowych opartych na wyobrażeniu bramki jako elementu, który coś przepuszcza lub nie przepuszcza.

Bramka jako… bramka

Nazwa „bramka” kojarzy się z bramą, drzwiami, wrotami, czyli w sumie z zamykaniem i otwieraniem.

I rzeczywiście, klasyczna bramka ma wiele wspólnego z otwieraniem i zamykaniem. Prawdziwa bramka to urządzenie, które albo przepuszcza sygnał, albo go nie przepuszcza. Niejako samorzutnie nasuwałby się tu wniosek, że bramka powinna mieć wejście sygnału, wyjście sygnału i jakieś wejście sterujące. Rzeczywiście, w przypadku elementów: OR, NOR, AND i NAND, wyobrażenie o bramce jako elemencie zamykającym i otwierającym drogę sygnału jest jak najbardziej słuszne.

Jeśli jedno z wejść wspomnianych bramek potraktujemy jako wejście sygnału (oczywiście logicznego), to pozostałe wejścia możemy traktować jako wejścia sterujące. Ideę zobaczysz na rysunku 7.

Bramka AND czy NAND zostanie otwarta tylko wtedy, jeśli na wszystkich wejściach sterujących będzie stan wysoki. Analogicznie, bramka OR czy NOR będzie otwarta, gdy na wszystkich wejściach sterujących jest stan niski.

Korzystając z rysunku 8 i podanych wcześniej informacji zastanów się, czy rzeczywiście tak jest. Takie rozumienie bramki będzie ci wręcz niezbędne, jeśli będziesz projektował układy, kierując się intuicją.

Doszliśmy tu do ważnego punktu naszych rozważań. Może zapytasz, po co aż cztery różne bramki? Czy nie wystarczyłaby jedna?

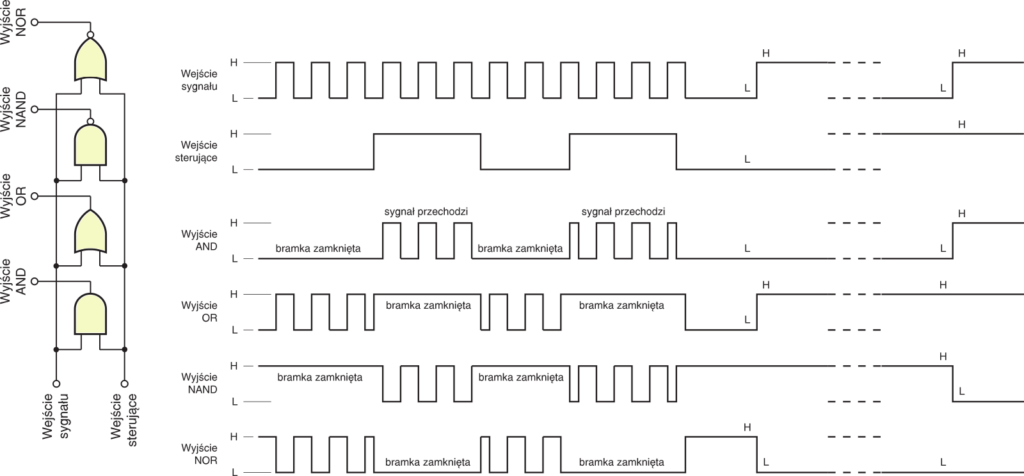
To jest dobre pytanie. Przypuszczam, że w pełni docenisz sprawę dopiero wtedy, gdy natkniesz się na kłopot: w jakimś układzie liczącym licznik będzie zliczał o jeden impuls za dużo lub za mało. Na razie dokładnie przeanalizuj rysunek 9 i zauważ czym w poszczególnych bramkach różni się sygnał na wyjściu, gdy bramka jest zamknięta, i gdy przepuszcza sygnał. Zwróć szczególną uwagę, co się dzieje na wyjściach w momentach zmiany stanu na wejściu sterującym.

W takiej roli bramki stosowane są na przykład w częstościomierzach, gdzie wzorcowy impuls otwiera bramkę na ściśle określony czas i umożliwia zliczanie impulsów podanych na wejście. W zależności od zastosowanego licznika, trzeba wykorzystać właściwą bramkę − do tej sprawy wrócimy jeszcze przy omawianiu liczników.

Oczywiście powyższe informacje o bramkowaniu nie dotyczą bramki NOT: mówimy o bramce NOT, a przecież nie ma tu mowy o żadnym bramkowaniu, tylko o zmianie sygnału logicznego na przeciwny. Ściśle biorąc, nie powinniśmy więc mówić „bramka NOT”, obecnie jednak często używa się pojęcia bramki w szerszym znaczeniu, i nie zdziw się, jeśli w literaturze spotkasz takie określenie. Zauważ, że w podręcznikach stosuje się zazwyczaj określenie „element NOT” lub „funktor NOT”. My, praktycy, zazwyczaj zamiast „bramka NOT” mówimy krótko „negator” lub „inwerter”.

A kolejny odcinek znajdziesz tutaj.

Piotr Górecki