Pierwsze kroki w cyfrówce – część 15

W poprzednich odcinkach zapoznałeś się z przerzutnikami. Omówiliśmy wspólnie zagrożenia związane z niedostatecznie ostrymi zboczami sygnałów zegarowych. Wiesz już, co to jest i jak działa prosty rejestr przesuwny. Po zapoznaniu się z przerzutnikami: D, T oraz JK jesteś w pełni przygotowany, by zrozumieć działanie wszelkich liczników.

Dzielniki i liczniki

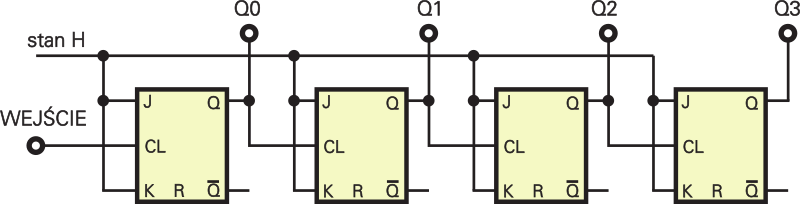
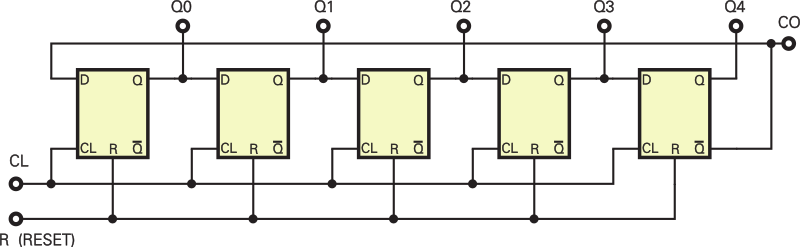
Nie jest dla ciebie tajemnicą, że przerzutnik T dzieli częstotliwość przez 2. Przeanalizujmy więc wspólnie, jak działa układ zestawiony z kilku takich przerzutników. Na rysunku 1 znajdziesz schemat takiego układu – jest to prosty licznik czterostopniowy, ale my zamiast czterostopniowy, częściej mówimy: czterobitowy. Przypuśćmy, że w roli przerzutników T pracują odpowiednio skonfigurowane przerzutniki JK z kostki CMOS 4027.

Ostatnio straszyłem cię różnymi pułapkami związanymi ze zbyt łagodnymi zboczami i opóźnieniami, więc być może podejrzliwie patrzysz na rysunek 1, znów spodziewając się jakiejś niespodzianki. W zasadzie masz rację – również tu występują pewne „kwiatki”, ale kwestią opóźnień i pułapek w tego typu układach zajmiemy się później.

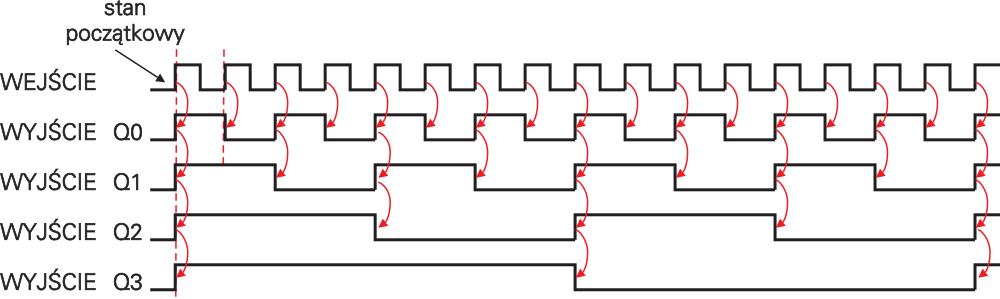
Na razie zacznij od podstaw i przeanalizuj przebiegi, jakie pojawiają się na wyjściach tego licznika przy podawaniu na wejście przebiegu prostokątnego. Pamiętaj, że w przerzutnikach JK z kostki 4027 zbocze dodatnie (rosnące) jest zboczem aktywnym. Sprawa jest beznadziejnie prosta: stan każdego kolejnego przerzutnika zmienia się na przeciwny, gdy na wejściu tego przerzutnika pojawi się zbocze rosnące. Przebiegi na poszczególnych wyjściach pokazane są na rysunku 2. Strzałkami zaznaczyłem ci, jak rosnące zbocza zmieniają stany poszczególnych przerzutników.

Wszystko jasne?

Do tej pory w artykułach serii „Pierwsze kroki w cyfrówce” konsekwentnie stosowałem określenia: stan (logiczny) niski oraz stan (logiczny) wysoki, a skrupulatnie unikałem popularnych określeń: zero logiczne i jedynka logiczna. Teraz, gdy doszliśmy do liczników, czas najwyższy zacząć mówić o liczbach. I dopiero teraz zacznę posługiwać się określeniami: zero, jedynka oraz kolejnymi liczbami naturalnymi. Stan logiczny wysoki na wyjściu licznika będziemy często nazywać jedynką, a stan niski zerem. Innych, pośrednich stanów tam być nie może (pomijając moment zmiany stanu).

Jeśli tylko zero i jedynka to…słusznie spodziewasz się, że na wyjściach licznika otrzymasz kolejne liczby przedstawione w systemie dwójkowym. W poniższej tabeli przypominam ci, jak w systemie dziesiętnym i dwójkowym zapisuje się liczby całkowite. Nie masz chyba wątpliwości, że dopisanie dowolnej ilości zer z lewej strony liczby niczego nie zmienia. Jeśli masz jakiekolwiek wątpliwości co do sposobu zapisu liczb w postaci dwójkowej, koniecznie poszukaj gdzieś w książce od matematyki i poznaj niezbędne podstawy.

DZIESIĘTNIE:	DWÓJKOWO:
000	000000
001	000001
002	000010
003	000011
004	000100
005	000101
006	000110
007	000111
008	001000
009	001001
010	001010
011	001011
012	001100
013	001101
014	001110
015	001111
016	010000
017	010001

Dla odróżnienia liczby dwójkowej 111 (dziesiętnie – siedem) od liczby dziesiętnej 111 (sto jedenaście), liczby dwójkowe albo poprzedza się dużą literą B, od angielskiego binary – dwójkowy, albo pisze się dużą literę B jako indeks za liczbą. Wygląda to albo tak: B111, albo 111_B. W pokrewnym systemie szesnastkowym, dla jasności analogicznie dopisuje się literkę H – hexadecimal, w systemie ósemkowym – literę O – octal, a niekiedy dla uniknięcia wątpliwości także w dziesiętnym literę D – decimal. Stąd 11_H to siedemnaście, 11_O to dziewięć, a 11_D to oczywiście jedenaście.

Spodziewasz się na pewno, że przy zliczaniu kolejnych impulsów wejściowych, na wyjściach licznika z rysunku 1 będą się pojawiać kolejne liczby dwójkowe. W rzeczy samej – na wyjściach tego licznika rzeczywiście pojawiają się kolejne liczby, ale…

Dobrze przypatrz się rysunkowi 2. Załóżmy, że w chwili początkowej na wszystkich wyjściach licznika był stan niski (same zera), czyli w liczniku była liczba zero. Po pierwszym narastającym zboczu zmienił się stan wyjść wszystkich przerzutników i na wyjściu pojawiła się liczba dwójkowa 1111, czyli dziesiętnie 15. Po drugim narastającym zboczu, w pierwszym stopniu licznika pojawiło się zero. A niby z której strony to zero dopisać? Czy da to liczbę 0111_B czy 1110_B? Pomyśl uważnie!

Na wyjściach licznika masz czterobitową liczbę dwójkową. Który bit jest „pierwszy”, a który „ostatni”? W układach cyfrowych nie mówimy o bicie „ pierwszym” lub „ostatnim”, tylko o bicie najbardziej znaczącym i bicie najmniej znaczącym. Najbardziej znaczący bit, nazywany też najstarszym, oznaczany jest MSB (Most Significant Bit), najmniej znaczący – czyli najmłodszy – LSB (Least Sig− nificant Bit).

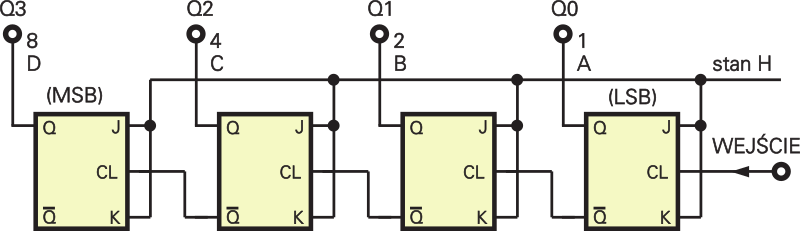
Przy okazji mała dygresja. Na rysunku 1 przerzutniki licznika narysowane są według powszechnej zasady, według której na schemacie przepływ sygnału następuje od lewej strony rysunku do prawej. Zasada ta jest rzeczywiście słuszna, ale rysując schematy liczników często od niej odchodzimy. Przyczyna jest prosta: przy takim uporządkowaniu jak na rysunku 1, najstarszy bit (wyjście Q3) narysowany jest z prawej strony, a to nie zgadza się z przyjętym sposobem zapisu liczb dwójkowych. Dlatego kolejne przerzutniki lub wyjścia liczników najczęściej rysuje się odwrotnie, by najstarszy bit wypadł z lewej strony, podobnie jak przy zapisie liczby na kartkę. Przykład tak narysowanego licznika znajdziesz na rysunku 3.

Na rysunku tym zaznaczono wagi kolejnych wyjść. Jak widać są to kolejne potęgi liczby 2, a mianowicie: 2⁰=1, 2¹=2, 2²=4, 2³=8, itd. Kolejne wyjścia liczników oznacza się czasami Q0, Q1, Q2… lub w przypadku liczników o czterech wyjściach częściej A, B, C, D. Wyjście A ma wagę 1, B – 2, C – 4, D – 8. W różnych źródłach można spotkać nieco odmienne oznaczenia wyjść licznika literą Q, Mianowicie można spotkać rysunki, gdzie wyjście pierwszego przerzutnika (czyli pierwszego stopnia licznika) oznaczone jest Q0, a na innych rysunkach oraz w katalogach to samo wyjście oznaczone jest Q1. W zasadzie nie ma tu żadnej sprzeczności. Q0 może oznaczać, że pierwsze wyjście ma wagę 2⁰ czyli 1, natomiast Q1 może oznaczać, że przebieg na tym pierwszym wyjściu ma częstotliwość 2¹ = 2 razy mniejszą niż przebieg na wejściu.

Uwaga! Literki A, B, C, D na wyjściach licznika nie mają nic wspólnego z cyframi używanymi w kodzie szesnastkowym (heksadecymalnym), gdzie A oznacza 10, B – 11, C – 12, D – 13.

Litery te nie mają także nic wspólnego z nazwą „liczniki BCD”. Licznik BCD – Binary Coded Decimal – dziesiętny kodowany dwójkowo, to taki licznik dwójkowy, który liczy tylko do dziesięciu. Liczniki BCD będą omówione w dalszej części artykułu.

Wracając do rysunków 1 i 2 można stwierdzić, że po drugim aktywnym zboczu stan licznika zmieni się na 1110_B. Kolejne stany licznika z rysunku 1 możesz prześledzić na rysunku 2: 0000 1111 1110 1101 1100 1011 1010 1001 1000 0111 0110 0101 0100 0011 0010 0001 0000 1111 itd…

Krótko mówiąc, rzeczywiście otrzymaliśmy licznik dwójkowy, ale… liczący wstecz

Co zrobić, by uzyskać licznik zliczający w przód?

Pomyśl samodzielnie!

Jeśli zaproponujesz umieszczenie negatorów na wszystkich wyjściach, to jest to jakiś pomysł, niezbyt doskonały, ale jest. Jeśli zaproponujesz dołączenie wejścia kolejnego licznika nie do wyjścia Q, tylko do wyjścia Q\ poprzedniego przerzutnika (według rysunku 3), załatwisz problem. Ale gdybyś chciał zrealizować taki licznik w postaci układu scalonego, będziesz miał kłopoty z połączeniem ze sobą kilku takich liczników. Samodzielnie w ramach ćwiczenia domowego narysuj przebiegi wejściowy i wyjściowe dla licznika z rysunku 3 i sam się przekonaj, że występuje tu coś w rodzaju opóźnienia o pół cyklu wejściowego.

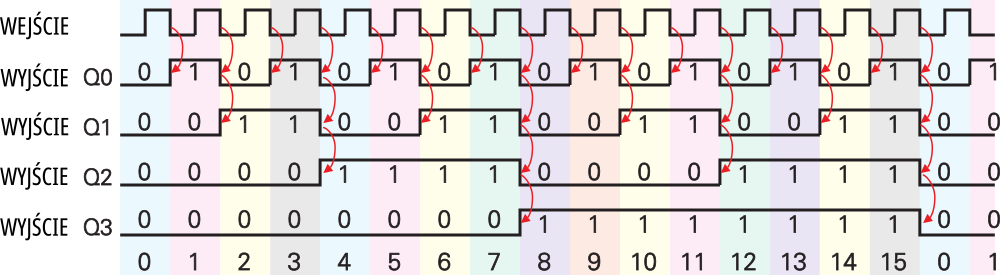
Ale licznik liczący w przód można wykonać prościej: wystarczy zastosować przerzutniki z aktywnym zboczem ujemnym (opadającym). Układ połączeń licznika będzie dokładnie taki sam, jak na rysunku 1, natomiast przebiegi będą inne, takie jak na rysunku 4. Przeanalizuj te przebiegi, bo oto doszedłeś do rozwiązania szeroko stosowanego w praktyce.

Masz przed sobą najprostszy (tak zwany asynchroniczny) licznik dwójkowy. Właśnie na takiej zasadzie zbudowane są liczniki CMOS 4020, 4024, 4040 (oraz 4060, który dodatkowo zawiera blok oscylatora). Nieco uproszczony schemat wewnętrzny liczników 4020, 4024 i 4040 pokazany jest na rysunku 3.

Wyprowadzenia tych kostek znajdziesz w kartach technicznych. Możesz (i raczej powinieneś) tam dopisać, że wszystkie wymienione powyżej liczniki mają wejście T wyposażone w obwód histerezy (bramka Schmitta), dzięki czemu mogą zliczać także impulsy o bardzo łagodnych zboczach, czyli długich czasach narastania. Jest to cecha ważna, zwłaszcza gdy liczniki zliczają impulsy nie pochodzące z innych układów logicznych. Układy te mają jeszcze wejście zerujące (R – reset). Powinieneś też wiedzieć, że wszystkie liczniki, rejestry i inne układy cyfrowe mają wyjścia buforowane. Buforowanie wyjść też ma ważne znaczenie, bowiem silne obciążenie, czy nawet zwarcie wyjścia nie wpływa na stan wewnętrznych obwodów licznika i układ zawsze pracuje prawidłowo.

Poznałeś właśnie pierwszą grupę liczników – tak zwane liczniki asynchroniczne. Mimo że są najprostsze, są bardzo często stosowane.

A teraz drobny konkursik. Odpowiedz na pytania:

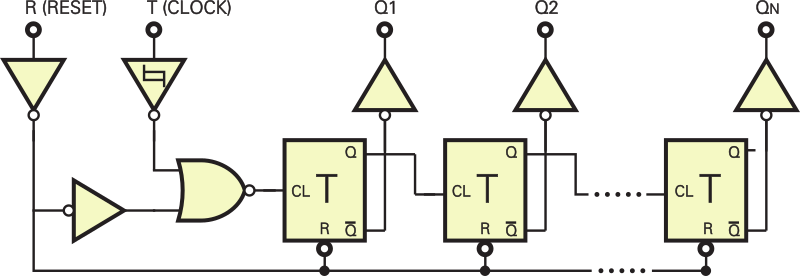
1. W którą stronę zlicza licznik z rysunku 5? W górę, czy w dół? Aktywne zbocze użytych przerzutników to zbocze rosnące.
2. Co się zmieni, jeśli aktywnym zboczem przerzutników będzie zbocze opadające?
3. Jakich zmian trzeba dokonać, by licznik zliczał w przeciwnym kierunku?

Odpowiedzi znajdziesz na końcu tego artykułu.

Inną grupą liczników są liczniki synchroniczne.

Liczniki synchroniczne

Liczniki synchroniczne są bardziej skomplikowane, na pierwszy rzut oka działają tak samo jak poprzednio opisane liczniki asynchroniczne. Wielu początkujących nie rozumiejąc, czym się różnią obawia się, czy aby nie popełnią błędu, stosując liczniki synchroniczne razem a asynchronicznymi.

Tymczasem dla elektronika−hobbysty w ogromnej większości przypadków zupełnie nie ma znaczenia, czy dany licznik jest synchroniczny, czy asynchroniczny. Istotne jest tylko to, jakie funkcje pełni dany licznik.

Ale nie wypada, by czytelnik nie miał bladego pojęcia o licznikach synchronicznych i żeby się ich bał.

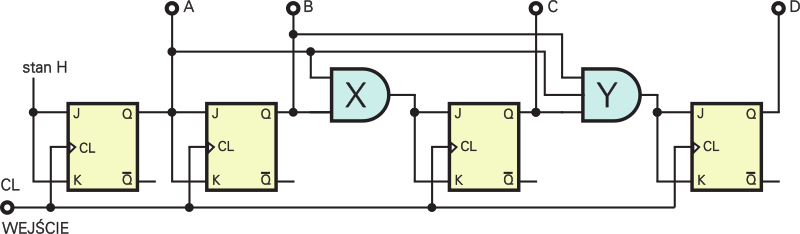
Na rysunku 6 możesz zobaczyć schemat prostego licznika synchronicznego.

Przede wszystkim zauważ, że sygnał zegarowy z wejścia podawany jest jednocześnie na wszystkie przerzutniki, a nie tylko na pierwszy przerzutnik, jak to jest w licznikach asynchronicznych. Oczywiście podczas kolejnego aktywnego zbocza zmieni się stan tych przerzutników, na których wejściach J, K występował stan wysoki. Najprościej ujmując, stan kolejnego przerzutnika zmienia się na przeciwny wtedy, gdy na wyjściach wszystkich poprzednich (młodszych) przerzutników występuje stan wysoki. Dbają o to bramki AND. W ramach samodzielnych ćwiczeń warto szczegółowo przeanalizować działanie licznika synchronicznego z rysunku 6.

Przeanalizuj działanie licznika, a przekonasz się, że jest ono takie jak na rysunku 2 lub 4.

Jeśli nie ma różnic, to w czym problem?

Różnica jednak jest – polega na tym, że w liczniku synchronicznym zmiany na wyjściach wystąpią jednocześnie, pod wpływem tego samego sygnału zegarowego. Jak to jednocześnie? A w liczniku asynchronicznym miałyby nie występować jednocześnie?

Pamiętaj, że każdy przerzutnik reaguje z opóźnieniem rzędu kilkunastu…kilku− dziesięciu nanosekund. Ale czy jest tu o co walczyć?

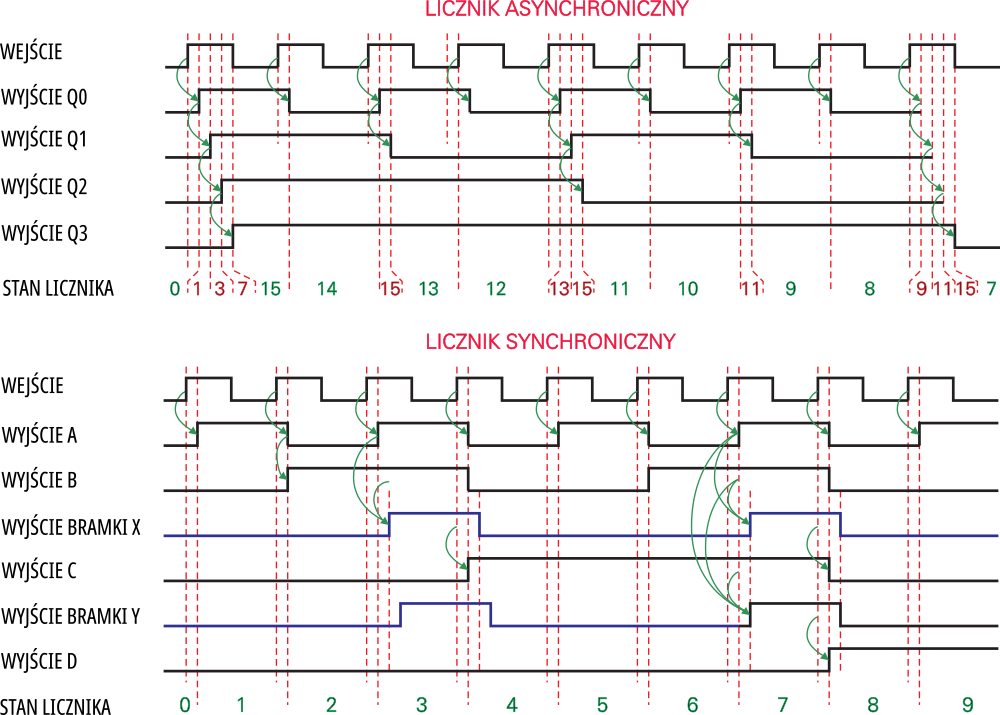
Na rysunku 7a i 7b zobaczysz przebiegi na poszczególnych wyjściach licznika asynchronicznego oraz synchronicznego (z przerzutnikami o aktywnym zboczu dodatnim) wzięte pod lupę. Tym razem przebieg wejściowy ma bardzo dużą częstotliwość i wyraźnie widać opóźnienia wprowadzane przez poszczególne składniki licznika. Zwróć uwagę na liczby u dołu rysunku pokazujące chwilowy stan licznika (reprezentowany przez liczbę dwójkową na wyjściach).

Jak widzisz, przebiegi w obu licznikach nie są identyczne: z uwagi na sumowanie się opóźnień przerzutników, na wyjściach licznika asynchronicznego pojawiają się błędne kody! Ale nie wpadaj w panikę! Po pierwsze, jeśli wykorzystujesz licznik asynchroniczny w charakterze dzielnika częstotliwości, i pobierasz sygnał z któregoś kolejnego wyjścia, opóźnienia te wcale nie będą ci przeszkadzać. Po drugie pamiętaj, że opóźnienia te są rzędu kilkudziesięciu czy co najwyżej kilkuset nanosekund. Czyli błędne kody będą pojawiać się na wyjściach licznika asynchronicznego tylko na tak krótki czas. Jeśli przykładowo taki licznik będzie sterował wyświetlaczem siedmiosegmentowym, w żaden sposób nie zauważysz jakichkolwiek nieprawidłowości. Zwróć uwagę, że nie są to błędy w zliczaniu (oba liczniki zawsze zliczają prawidłowo), tylko chwilowe błędy w podawaniu wyniku. Takie błędy mogłyby dać o sobie znać tylko w nielicznych układach, gdzie na bieżąco sprawdzany byłby stan wyjść licznika i stan ten wpływałby na pracę jakiejś dalszej części układu. Przykładowo są sytuację, gdy do wyjść licznika dołączony jest tak zwany komparator cyfrowy, czyli układ scalony, który porównuje zawartość licznika z zadaną liczbą. Wtedy komparator może przez wspomniane nanosekundowe odcinki czasu dawać błędne wyniki. Takie rozwiązania są jednak rzadkością.

Jeśli mimo wszystko opóźnienia byłyby niepożądane, a ewentualne błędne kody – groźne, należy po prostu zastosować licznik synchroniczny, w którym zmiany na wyjściach następują praktycznie w tym samym momencie (z dokładnością do pojedynczych nanosekund).

Rysunek 7b pokazuje, że w liczniku synchronicznym również mamy do czynienia z opóźnieniami, ale zastosowane rozwiązanie gwarantuje jednoczesne przełączanie wszystkich wyjść.

Tu warto nadmienić o maksymalnej częstotliwości zliczania. Łatwo się domyślić, że w liczniku asynchronicznym maksymalna częstotliwość zliczania jest wyznaczona przez pierwszy stopień – pierwszy przerzutnik, bo już następny pracuje z częstotliwością dwukrotnie mniejszą, itd. Natomiast w liczniku synchronicznym maksymalna częstotliwość jest wyznaczona nie przez sumę opóźnień wszystkich przerzutników, tylko przez sumę dwóch opóźnień: jednego przerzutnika oraz opóźnienie bramki. Trzeba uwzględnić opóźnienie wnoszone przez bramkę, bo sygnał na wejściach J, K wszystkich przerzutników musi się ustalić przed nadejściem następnego aktywnego zbocza sygnału zegarowego.

Z tego można szybko wyciągnąć wniosek, że liczniki synchroniczne mogą pracować przy większych częstotliwościach, niż liczniki asynchroniczne. W większości przypadków tak, ale nie zawsze. To są jednak szczegóły, które nie są dla ciebie najważniejsze.

Ważne jest, że te drobne różnice w działaniu liczników synchronicznych i asynchronicznych zwykle nie mają w praktyce istotnego znaczenia. Przy projektowaniu większości układów nie zastanawiamy się nad tym, co to za licznik, a jedynie szukamy kostki, która ma możliwości potrzebne do danego zastosowania.

Inne liczniki

Dwa podane wcześniej przykłady być może przekonały cię, że liczniki zawsze liczą w kodzie dwójkowym. Jest to przekonanie błędne. Zastanów się: często liczniki wykorzystywane są w charakterze dzielników częstotliwości – nie jest wcale ważne, jakie liczby pojawiają się na wyjściach licznika, istotne jest tylko, że na którymś z wyjść częstotliwość przebiegu jest ileś razy mniejsza, niż częstotliwość na wejściu.

Do takiej roli niekoniecznie trzeba wykorzystać licznik zliczający w kodzie dwójkowym. Zgadzasz się? Niewykluczone, że podane przykłady doprowadziły cię do wniosku, że licznik można wykonać z różnych przerzutników i wieloma sposobami. Słusznie! Czy słyszałeś o licznikach pracujących w kodzie Gray a, kodzie +3 czy kodzie Aikena. Nie słyszałeś? To masz szczęście – kiedyś, gdy pojawiły się pierwsze przerzutniki i liczniki budowane z pojedynczych bramek, stosowano przeróżne układy połączeń i różne realizacje. Takie fikuśne liczniki często nie dawały na wyjściach kolejnych liczb dwójkowych. Dawały inne, wymyślne sekwencje liczb.

Na twoje szczęście stosunkowo szybko pojawiły się układy scalone zawierające gotowe liczniki. Pewna część spośród nich zyskała dużą popularność, inne zupełnie znikły z rynku. W następnym artykule poznasz bliżej kilka najpopularniejszych liczników. Zapoznasz się z licznikami dwukierunkowymi, czyli rewersyjnymi, które według potrzeb mogą zliczać albo w górę, albo w dół. Poznasz liczniki programowane, do których można wstępnie wpisać jakąś liczbę i od niej rozpocząć zliczanie. Takie wynalazki (liczniki programowane zliczające w dół) są bardzo przydatne na przykład do odliczania zadanej ilości impulsów czy zdarzeń. Nie będę cię jednak męczył szczegółami budowy wewnętrznej, bo nie jest ci to niezbędne. Wiedza, którą posiadłeś na temat bramek i przerzutników powinna ci wystarczyć, byś z grubsza wyobraził sobie, jak mogą być zbudowane takie liczniki.

A teraz chyba cię mocno zaskoczę układem z rysunku 8.

Czy to jest licznik?

Przecież to jest jakiś rejestr, a nie licznik!

W rzeczy samej, jest to pięciostopniowy rejestr, w którym wejście pierwszego stopnia połączone jest z zanegowanym wyjściem ostatniego stopnia. Na rysunku 9 znajdziesz przebiegi tego licznika. I co? Niewątpliwie jest to układ mający dziesięć różnych stanów na wyjściach, a więc… jest to licznik zliczający do dziesięciu! Na pewno nie jest to jednak licznik dwójkowy…

Taki licznik nazywany jest licznikiem Johnsona. A na co komu taki „dżonson”? Może cię zaskoczę informacją, że jeden z ulubionych liczników, mianowicie CMOS 4017 to właśnie licznik Johnsona, tyle że wyposażony w dodatkowy dekoder, dający w danej chwili stan wysoki tylko na jednym z dziesięciu wyjść. Analizując rysunek 9 dowiesz się także, jaki przebieg występuje na wyjściu CO (nóżka 12) kostki 4017 – jest to zanegowany przebieg z wyjścia ostatniego przerzutnika, czyli Q4\. Podobny licznik, tylko składający się z czterech przerzutników, a więc zliczający do ośmiu, dostępny jest jako układ scalony CMOS 4022.

Nasza ulubiona kostka 4017 znakomicie zastępuje zespół dwóch kostek: licznik dwójkowy (np. 4040) z dołączonym dekoderem (np. 4028). A czym jeszcze różni się licznik Johnsona z dekoderem, od zespołu licznik asynchroniczny plus dekoder kodu dwójkowego na kod 1 z 10?

Rysunek 7a przekonuje, że na wyjściu dekodera współpracującego z licznikiem asynchronicznym na krótko (na jakieś dziesiątki czy setki nanosekund), ale jednak, pojawią się błędne kody. Natomiast zarówno w liczniku synchronicznym, jaki w dziwnym liczniku Johnsona z dekoderem błędnych kodów nie ma! Powód jest dość prosty: przemyśl to sam, albo poszukaj w książkach. A przy okazji jeszcze jedno ćwiczenie. Patrząc na rysunki 8 i 9 spróbuj zaprojektować jak najprostszy dekoder 1 z 10, który będzie miał 10 wyjść i przetworzy pięć sygnałów Q0…Q4 licznika, by przy zliczaniu kolejnych impulsów stan wysoki występował tylko na jednym, kolejnym wyjściu. Uzyskaj na wyjściach dekodera przebiegi jak na rysunku 10. Do dyspozycji masz 10 dwuwejściowych bramek AND i 10 negatorów. Powodzenia!

Przy okazji jeszcze raz przypominam ci, że w ogromnej większości przypadków, wspomniane króciutkie fałszywe impulsy na wyjściach licznika asynchronicznego i współpracującego z nim dekodera nie zaszkodzą, jednak powinieneś wiedzieć o tym zjawisku. Gdyby spowodowało ono błędne działanie dalszych części układu, niczego nie będziesz w stanie wykryć, obserwując przebiegi wyjściowe prostym oscyloskopem. Tu znów potrzebna jest wiedza, bo zapewne długo nie będzie cię stać na oscyloskop pozwalający zaobserwować nanosekundowe szpilki i nanosekundowe opóźnienia. Gdy będziesz rozumiał przedstawione zagadnienie, będziesz miał oscyloskop w głowie i w oku. Już patrząc na schemat przeanalizujesz opóźnienia i wykryjesz ewentualne szkodliwe szpilki. Jest to bardzo ważna cecha dobrego konstruktora układów cyfrowych. Właśnie dlatego podaję ci zadania do samodzielnego przemyślenia.

Powrócimy też na chwilę do kwestii numeracji wyjść. Na rysunku 8 wyjścia poszczególnych stopni oznaczyłem Q0…Q4. Oczywiście licznik nie zlicza w kodzie dwójkowym, więc tym razem nie możemy powiedzieć, że dane wyjście „ma jakąś wagę”. Wyjścia są jakby równorzędne, nie ma najstarszego i najmłodszego, licznik ma po prostu 10 różnych kombinacji na swych wyjściach.

Jak widzisz, nie ma jednego ustalonego i precyzyjnego sposobu oznaczania wyjść. W różnych katalogach i podręcznikach stosuje się jeszcze inne oznaczenia. Nie ma ratunku – musisz rozumieć działanie liczników, rejestrów i innych wynalazków, by nie dać się „wpuścić w kanał” takim i podobnym oznaczeniom.

Odpowiedzi dotyczące konkursu :

1. Licznik z rysunku 5 zlicza w dół.
2. Jeśli aktywnym zboczem przerzutników będzie zbocze opadające to licznik zacznie liczyć w przód. Jednak licznik będzie zliczał kolejne impulsy dopiero na zboczu opadającym drugiego półokresu przebiegu zegarowego.
3. Aby licznik liczył w przód na pierwszym zboczu narastającym sygnału zegarowego (w pierwszym półokresie) należy zastąpić bramkę NOR bramką OR oraz aktywnym zboczem przerzutników musi być zbocze opadające (najprościej to osiągnąć dodając negator do każdego wejścia zegarowego przerzutników pokazanych na rysunku 5).

A kolejny odcinek cyklu znajdziesz tutaj.

Piotr Górecki