Filtry aktywne – część 9
W poprzednim odcinku zajmowaliśmy się filtrami dolnoprzepustowymi Sallen−Keya. W tym odcinku zajmiemy się filtrami środkowoprzepustowymi.
Jak zwykle artykuł zawiera gotowe proste recepty. Skorzystanie z nich jest bardzo łatwe, o czym przekonują zaprezentowane przykłady. Aby w pełni skorzystać z podanego materiału, konieczne jest przyswojenie sobie informacji ze wszystkich odcinków wstępnych, począwszy od pierwszego artykułu cyklu.
Filtr pasmowy z wielokrotnym sprzężeniem zwrotnym
W przypadku filtru pasmowego dobroć nie musi być i zwykle nie jest równa 0,5 czy 0,707. Jeśli filtr ma przepuszczać sygnały w bardzo wąskim paśmie, dobroć musi być odpowiednio duża, na pewno większa niż 1. Dobroć nie powinna być większa niż 10 (dobroć 10 daje wąski i stromy filtr). Pamiętaj jednak, że filtr o większej dobroci dłużej „dzwoni”, czyli drgania na wyjściu utrzymują się po zaniku sygnału wejściowego. Czym większa dobroć, tym pasmo jest węższe, ale też filtr dłużej „dzwoni” po zaniku sygnału.
Ze względu na różne wartości dobroci, tym razem wzory nie będą aż tak proste, jak poprzednio, ale za to pozwolimy sobie na dodatkowy luksus: projektowany filtr nie musi mieć wzmocnienia równego 1 w paśmie przepustowym − może przy okazji wzmacniać sygnał. Wzmocnienie nie powinno jednak przekraczać 10× (20 dB).
Tylko proszę, nie szalej. Czym większe wzmocnienie i większa dobroć, tym trudniejsze zadanie ma wzmacniacz operacyjny, zwłaszcza przy większych częstotliwościach. Nie żądaj więc jednocześnie i dużego wzmocnienia, i dużej dobroci. Dla bezpieczeństwa stosuj zasadę, że iloczyn dobroci i wzmocnienia nie powinien przekraczać 10.
Zaczynajmy!
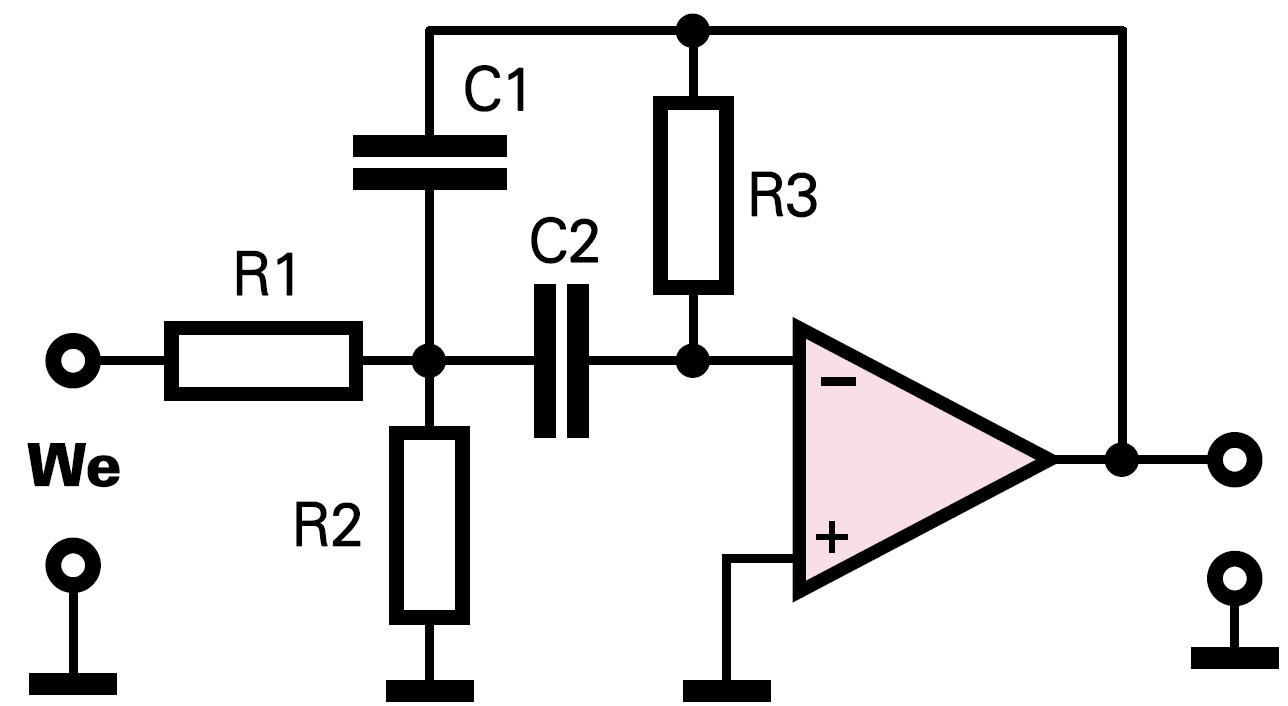
Aby obliczyć wartości elementów filtru według rysunku 1, musisz wiedzieć czego chcesz, czyli znać wartości:
częstotliwości środkowej fs
dobroci Q
wzmocnienia G.
Znając częstotliwość środkową, najpierw obliczamy pojemność ze wzoru:
C [nF] = 10000 [nFHz] / f [Hz]
Pojemność wychodzi w nanofaradach, jeśli częstotliwość podasz w hercach. Jak zawsze, decydujesz się na najbliższą wartość z szeregu E6 (1; 1,5; 2,2; 3,3; 4,7; 6,8; 10).
Oba kondensatory będą jednakowe: C=C1=C2
Obliczasz reaktancję wybranego kondensatora przy częstotliwości środkowej:
![]()
Jak zwykle podstawiasz tu wybraną wartość pojemności z szeregu E6, a nie wartość wcześniej obliczoną ze wzoru. Reaktancja wychodzi w kiloomach, jeśli częstotliwość podamy w hercach, a pojemność w nanofaradach.
Teraz już obliczysz wartości rezystorów z (wbrew pozorom) prostych wzorów:
R1 = Xc × (Q/G)
R2 = Xc × [Q / (2Q2−G)]
R3 = Xc × (2Q)
To wszystko!
Przykłady
Chcemy, żeby nasz filtr miał częstotliwość środkową równą 2 kHz, żeby pasmo przenoszenia (−3 dB) wynosiło 500 Hz. Dobrze byłoby, żeby filtr wzmacniał sygnał. Pasmo 500 Hz przy częstotliwości 2 kHz oznacza, że dobroć ma wynosić 4 (2 kHz/500 Hz). Wzmocnienie nie powinno być zbyt duże, zgodnie z wcześniejszymi zaleceniami niech wynosi 2 (+6 dB).
Mamy więc fs = 2 kHz, Q = 4 i G = 2.
Obliczamy:
C [nF] = 10000 [nFHz] / 2000 [Hz] C = 5 nF
Oczywiście zastosujemy C=4,7 nF. Oba kondensatory będą jednakowe: C=C1=C2
Xc [kΩ] = 160000 / 2000 [Hz] × 4,7 [nF] Xc = 17 kΩ
I dalej:
R1 = 17 kΩ × (4/2) = 34 kΩ
R2 = 17 kΩ × [4 / (2(4)2− 2)] = 17 kΩ × (4/30) = 17 kΩ × 0,133 = 2,27 kΩ
R3 = 17 kΩ × (2 × 4) = 136 kΩ
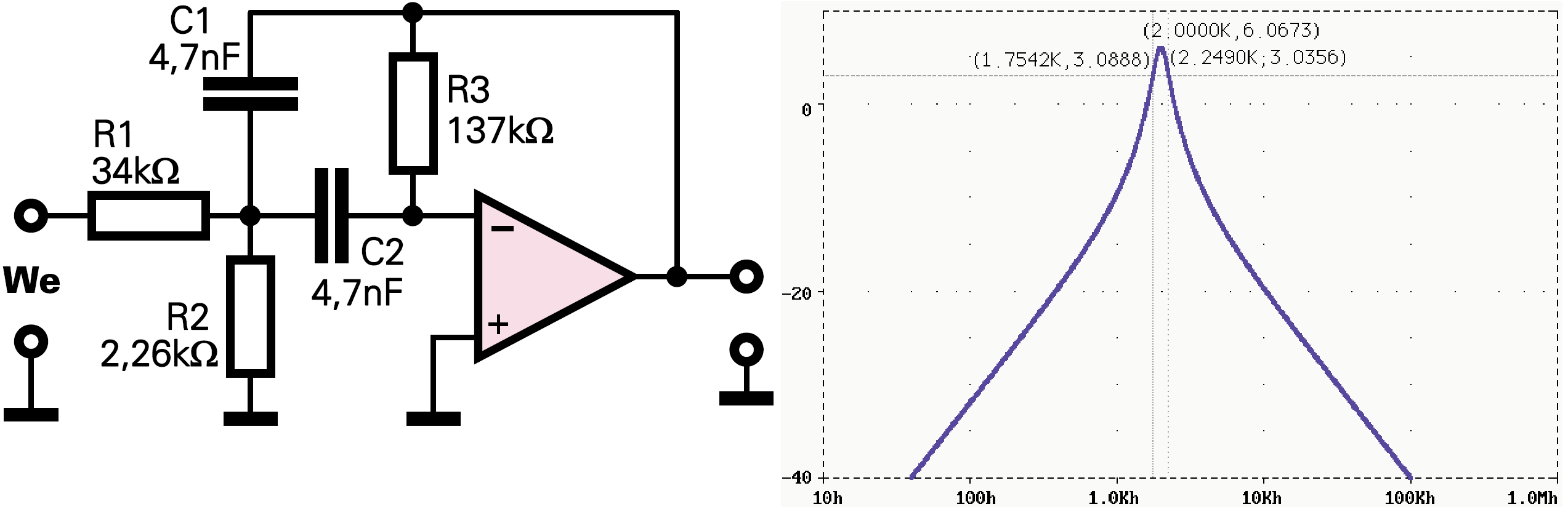
Zastosujemy rezystory 1−procentowe: R1 = 34,0 kΩ, R2 = 2,26 kΩ, R3 = 137 kΩ. Układ i charakterystyka pokazane są na rysunku 2.
Wynik jak najbardziej zgadza się z obliczeniami.
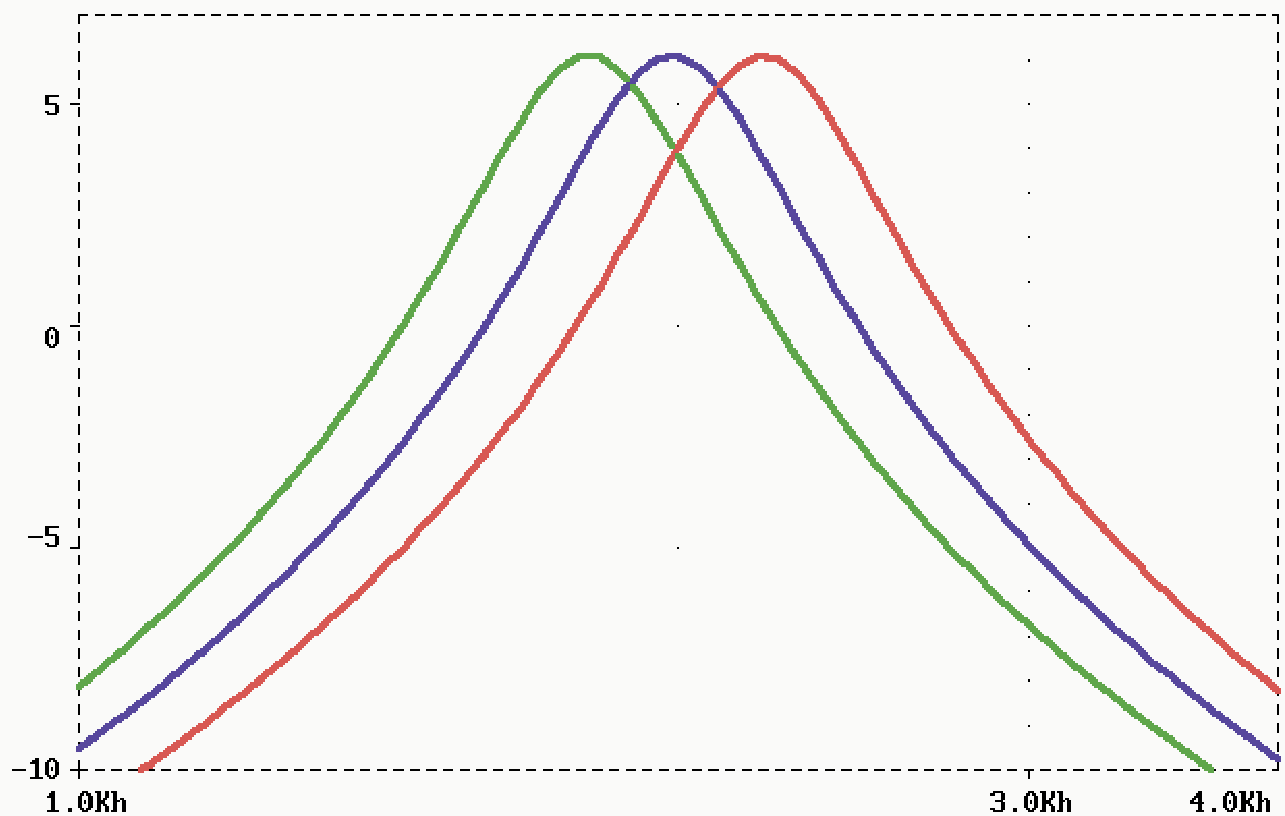
W przypadku filtrów górno− i dolnoprzepustowych drobne zmiany częstotliwości granicznej wynikające z tolerancji kondensatorów są zazwyczaj nieistotne i nie trzeba ich korygować. Podobnie jest z niektórymi filtrami pasmowymi (zwłaszcza o małej dobroci). Zazwyczaj jednak przy projektowaniu filtrów pasmowych trzeba pamiętać o nieuchronnych rozrzutach i razie potrzeby je skorygować. Rysunek 3 pokazuje trzy charakterystyki: idealną (niebieska) i przy skrajnych wartościach tolerancji 10−procentowych kondensatorów (zielona i czerwona).
Jak widać, zmiany są znaczne i nie można ich pominąć. Aby uniknąć takich niespodzianek, należałoby dobierać kondensatory z tolerancją 1% i stosować precyzyjne rezystory. Dobór kondensatorów w warunkach amatorskich jest trudny, bo popularne mierniki uniwersalne z funkcją pomiaru pojemności są zwykle bardzo mało dokładne − dokładność jest znacznie gorsza niż 1%. Mogą więc służyć co najwyżej do dobrania jednakowych kondensatorów, co jest jak najbardziej pożądane.
Zamiast precyzyjnie dobierać wartość kondensatorów z tolerancją co najmniej 1%, wystarczy zastosować dobrane pary jednakowych kondensatorów, a ewentualne odchyłki skorygować w prosty sposób, zmieniając wartość R2, w praktyce stosując zamiast R2 rezystor i dobry potencjometr montażowy. Co ciekawe, zmiana wartości R2 nie wpłynie na pozostałe parametry filtru.
Na marginesie warto wspomnieć, że filtr pasmowy z rysunku 1 ma szereg interesujących i bardzo cennych właściwości. Można niezależnie korygować parametry, a takie regulacje nie wpływają na siebie. Wzmocnienie filtru wyznacza stosunek R3 do R1 (G=R3/2×R1), korektę wzmocnienia przeprowadzamy w razie potrzeby zmieniając R1.
Zmieniając w równych proporcjach R2, R3 zmieniamy częstotliwość, przy stałej dobroci. Niestety, nie można tu wykorzystać podwójnego potencjometru, bo wartość R3 jest zawsze dużo większa niż R2.
Filtr możemy bardzo łatwo przestrajać, i to w szerokich granicach, zmieniając tylko R2. R2 nie musi być rezystorem czy potencjometrem, tylko na przykład tranzystorem J−FET lub potencjometrem elektronicznym. Przy takiej regulacji pasmo pozostaje stałe, a więc zmienia się dobroć filtru, co nie jest korzystne.
Zaprezentowany moduł filtru pasmowego może być wykorzystany samodzielnie, ale można też z kilku modułów połączonych w szereg budować bardziej złożone filtry. Do takich eksperymentów niezbędny jest program do komputerowej symulacji, który pomoże szybko dobrać potrzebną charakterystykę.
W następnym odcinku zajmiemy się filtrami pasmowymi o dużej dobroci.
Piotr Górecki