Elektronika (nie tylko) dla informatyków (21) Szeregowy obwód rezonansowy

W poprzednim odcinku zajmowaliśmy się drganiami swobodnymi obwodu LC. W tym odcinku bierzemy na warsztat szeregowy obwód rezonansowy.

Możemy w dużym skrócie powiedzieć, że po naładowaniu kondensatora napięciem stałym, obwód LC staje się swego rodzaju generatorem drgań – zamienia napięcie stałe na drgania sinusoidalne. Jednak w praktyce we wszystkich obwodach LC występują straty, co powoduje, że wytwarzane drgania stopniowo zanikają. Straty te na schemacie zastępczym są reprezentowane przez rezystancję, która jak wiadomo, zamienia energię elektryczną na ciepło.

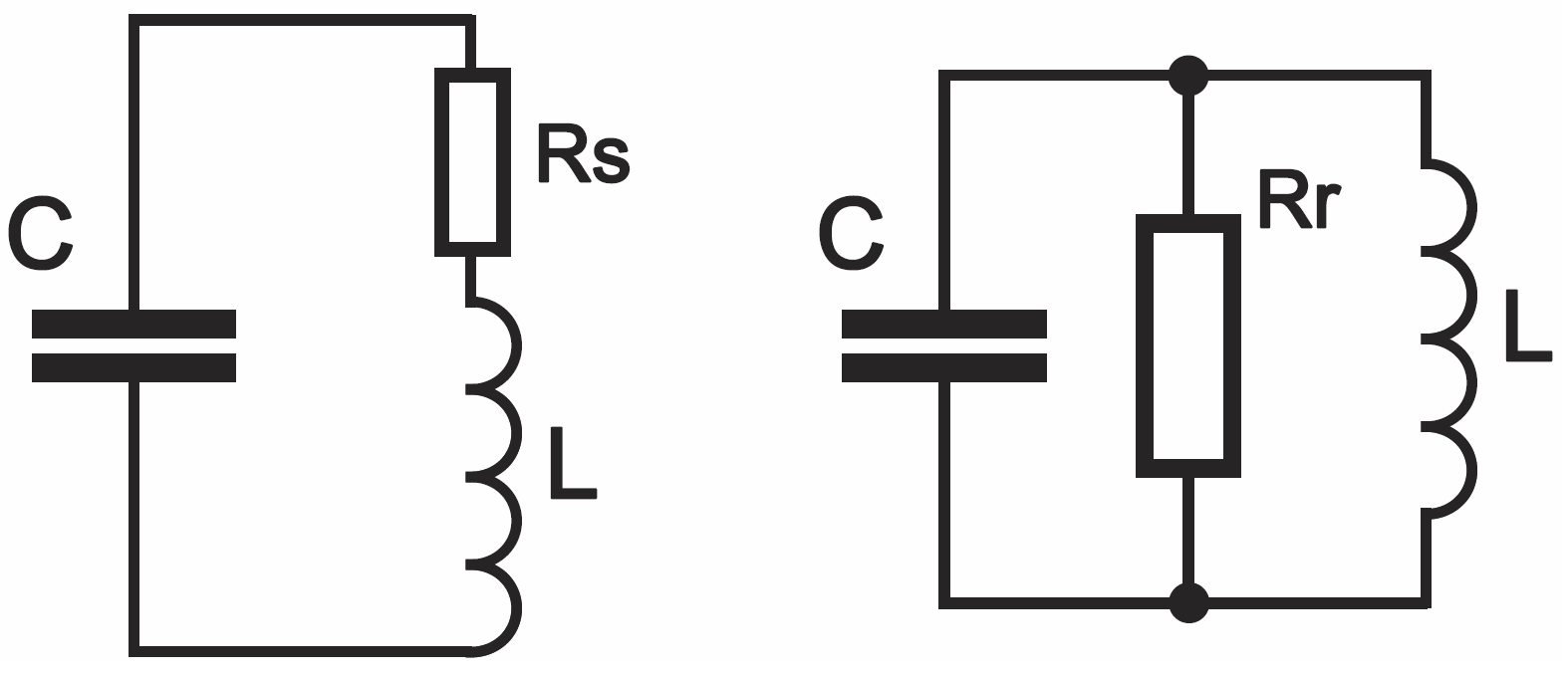
W poprzednim odcinku zaznaczyliśmy te straty jako rezystancję włączoną w szereg z cewką, co jest o tyle logiczne i sensowne, że większość tych strat to rezystancja drutu cewki. Jednak pamiętaj, że mówimy tu o schemacie zastępczym, który w sposób uproszczony i łatwy do analizy ma przedstawić właściwości rzeczywistego układu. Na takim uproszczonym schemacie straty równie dobrze możemy zaznaczyć jako rezystancję równoległą z L i C. Mamy więc przynajmniej dwie możliwości przedstawienia strat w obwodzie LC, jak pokazuje rysunek 1.

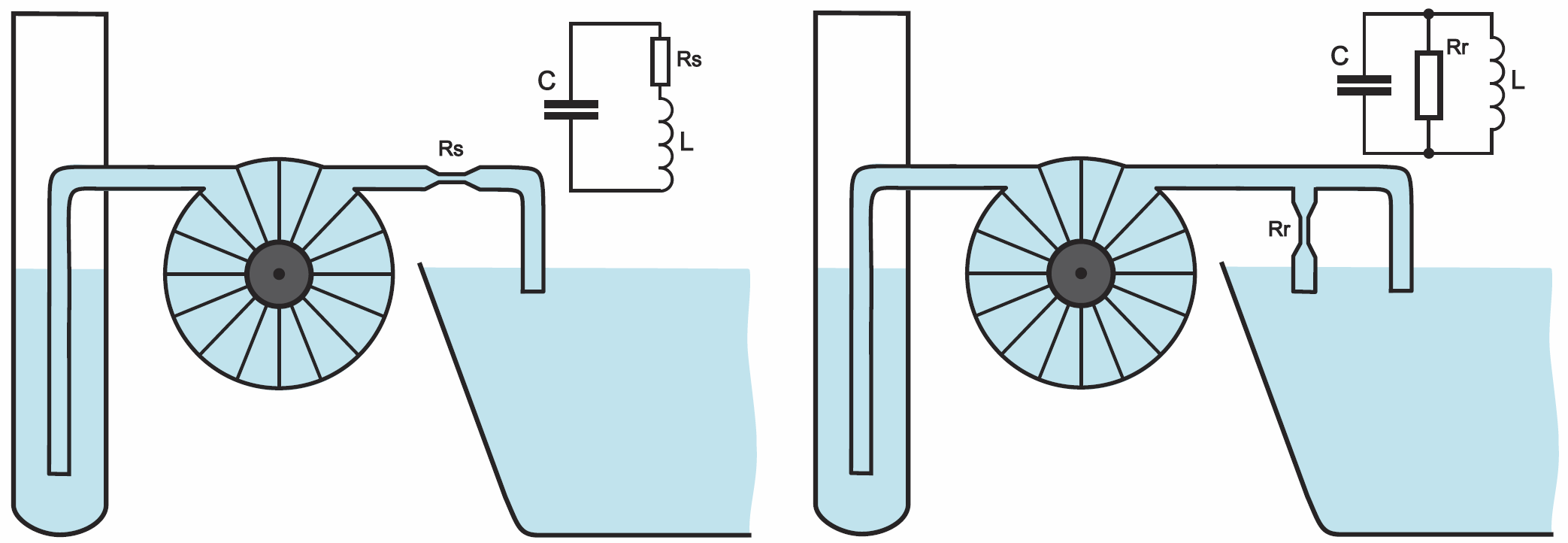
Tak samo w analogii hydraulicznej straty moglibyśmy przedstawić na dwa sposoby, jak przedstawia rysunek 2 i w obydwu przypadkach efekt byłby jednakowy – stopniowe zmniejszanie amplitudy drgań.

Oczywiście dla schematów zastępczych z rysunku 1, dotyczących danego obwodu LC, wartości zastępczych rezystancji szeregowej R_s i równoległej R_r nie będą jednakowe. Słusznie domyślasz się, że w praktycznych obwodach, których dobroć jest rzędu kilkunastu do kilkuset, szeregowa rezystancja R_s będzie mała, dużo mniejsza od oporności charakterystycznej . Z kolei zastępcza równoległa rezystancja strat R_r dla tego samego obwodu będzie duża, dużo większa od oporności charakterystycznej. Występuje tu prosta zależność:

Q = ρ/R_s           Q = R_r/ρ

czyli

R_s = ρ/Q           R_r = ρ×Q

Podkreślam, że chodzi o ten sam rzeczywisty obwód LC ze stratami i straty te możemy przedstawić na dwa sposoby: albo jako rezystancja szeregowa R_s, albo jako rezystancja równoległa R_r. Mamy więc do wyboru dwa modele, przedstawiające właściwości tego samego obwodu. Tylko po co?

Otóż obwody LC niezmiernie rzadko, o ile w ogóle, służą do zamiany napięcia stałego na przebieg sinusoidalny.

Za to często pełnią rolę filtrów. A to jest związane z faktem, że obwód LC „lubi częstotliwość swych drgań swobodnych”. Przy pracy obwodów LC w roli filtrów wykorzystujemy zjawisko rezonansu. A przy analizie obwodów rezonansowych przydatne będą oba modele.

Rezonans i obwód rezonansowy

Zauważ, że do tej pory nie używałem określeń związanych z rezonansem, a przecież powszechnie mówimy o obwodzie rezonansowym LC i o częstotliwości rezonansowej obwodu LC, a nie o częstotliwości drgań własnych, swobodnych (jednokrotnie pobudzonego) obwodu LC czy RLC. Otóż ściślej biorąc, rezonans to różne zjawiska fizyczne, dotyczące drgań wymuszonych. Jeśli chcesz, samodzielnie poszukaj wyjaśnienia, co to jest rezonans. W każdym razie o rezonansie mówimy wtedy, gdy mamy jakiś czynnik pobudzający, co oznacza też dostarczanie energii i interesuje nas specyficzna reakcja systemu na ten czynnik pobudzający. Ta reakcja jest specyficzna, ponieważ wiąże się ze zwiększaniem wielkości drgań przy pewnych częstotliwościach, charakterystycznych dla danego systemu.

Rezonans dotyczy nie tylko obwodów elektrycznych. Bodaj najbardziej znanym, podręcznikowym przykładem rezonansu jest katastrofa mostu w Angers (wcale nie pierwsza ani jedyna tego typu). Otóż w roku 1850 batalion piechoty francuskiej, przechodząc równym krokiem, tak rozkołysał ten most, że uległ on całkowitemu zniszczeniu, powodując 226 ofiar (fotografia 3).

Nas interesują obwody LC, a właściwie obwody RLC, które bardzo często pracują w warunkach pobudzania z zewnątrz: doprowadzamy do obwodu RLC czynnik pobudzający i obserwujemy specyficzne zjawiska. U nas, w elektronice, tym czynnikiem pobudzającym są przebiegi elektryczne. Ogólnie biorąc, rezonans polega na tym, że obwód LC „najbardziej lubi” sygnały o częstotliwości drgań własnych. I jeśli doprowadzimy do obwodu LC przebiegi sinusoidalne „o ulubionej częstotliwości”, wystąpią tam zaskakujące zjawiska.

A jeśli do obwodu LC, lub raczej RLC, trzeba doprowadzić sinusoidalny sygnał wymuszający, to w grę wchodzą przynajmniej dwie podstawowe możliwości. Nieprzypadkowo w podręcznikach najczęściej analizuje się dwa przypadki: rezonansu szeregowego i rezonansu równoległego. Podkreślam jeszcze raz, że rezonans obserwujemy wtedy, gdy pobudzamy obwód LC sygnałem podawanym z zewnątrz. Dla ułatwienia analizy interesować nas będą sinusoidalne przebiegi pobudzające, wytwarzane przez źródło napięciowe (generator sinusoidalny). Zacznijmy od obwodu szeregowego.

Szeregowy obwód rezonansowy

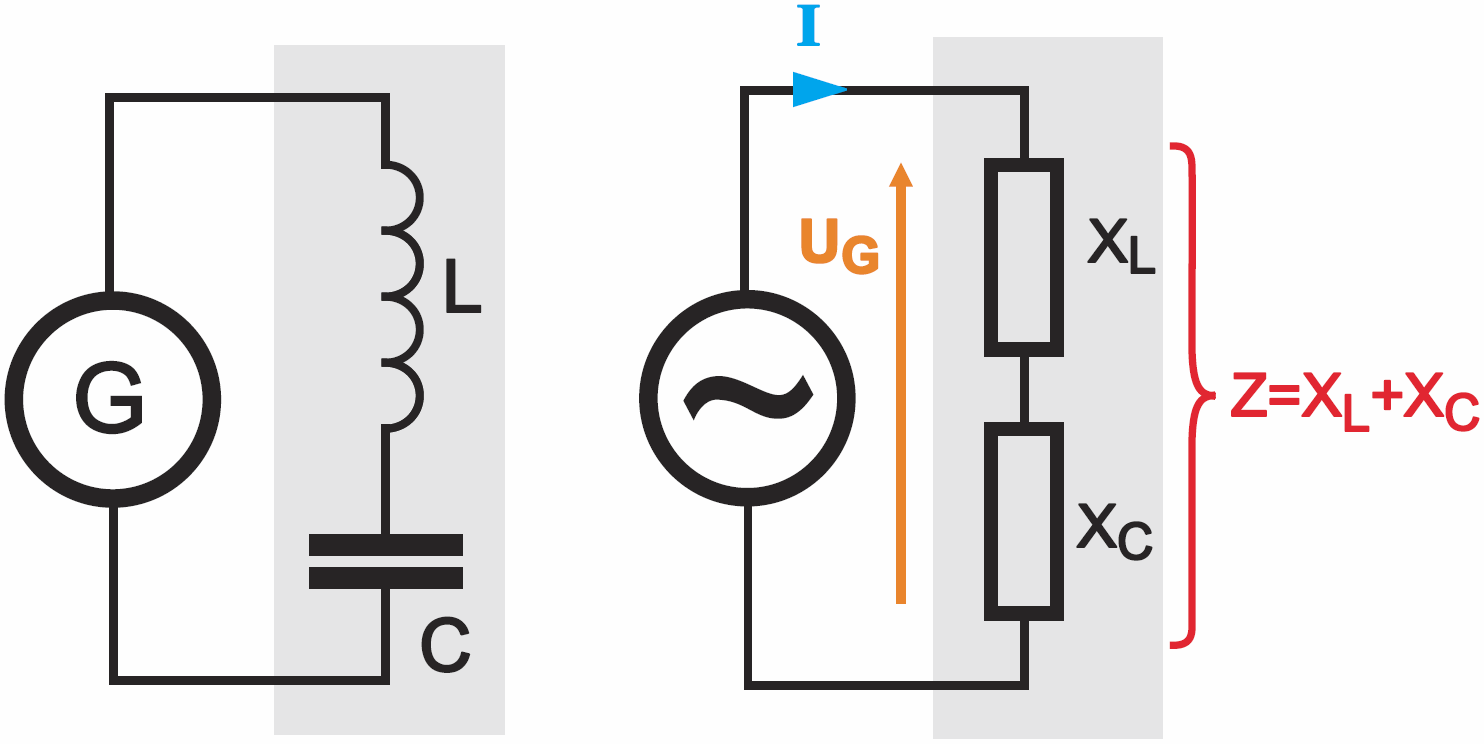
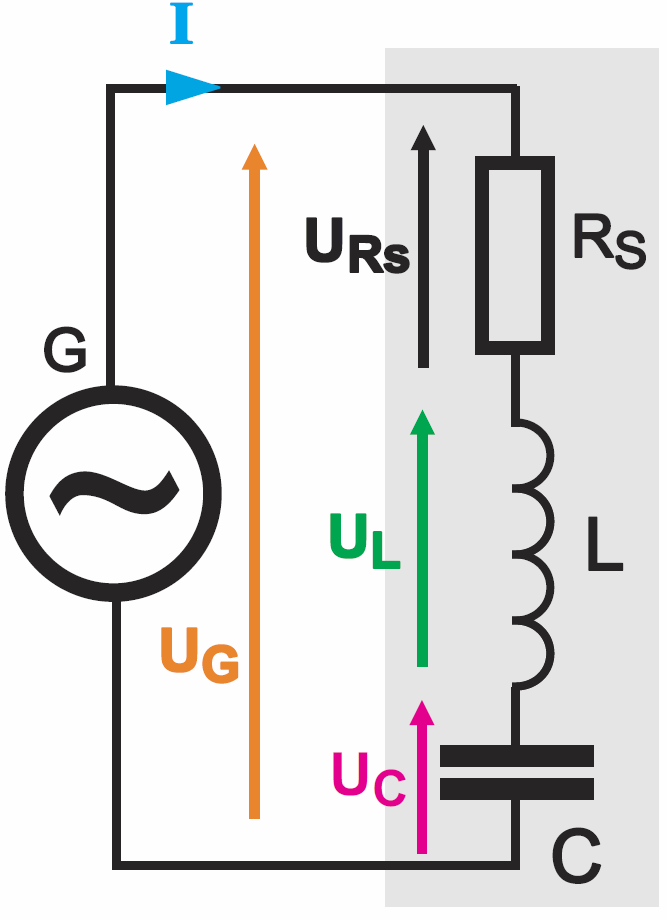
Zastanówmy się najpierw nad opornością szeregowego obwodu LC – rysunek 4. Mamy tu szeregowe połączenie elementów, więc oporności, ściślej reaktancje X_L i X_C, niewątpliwie należy dodać.

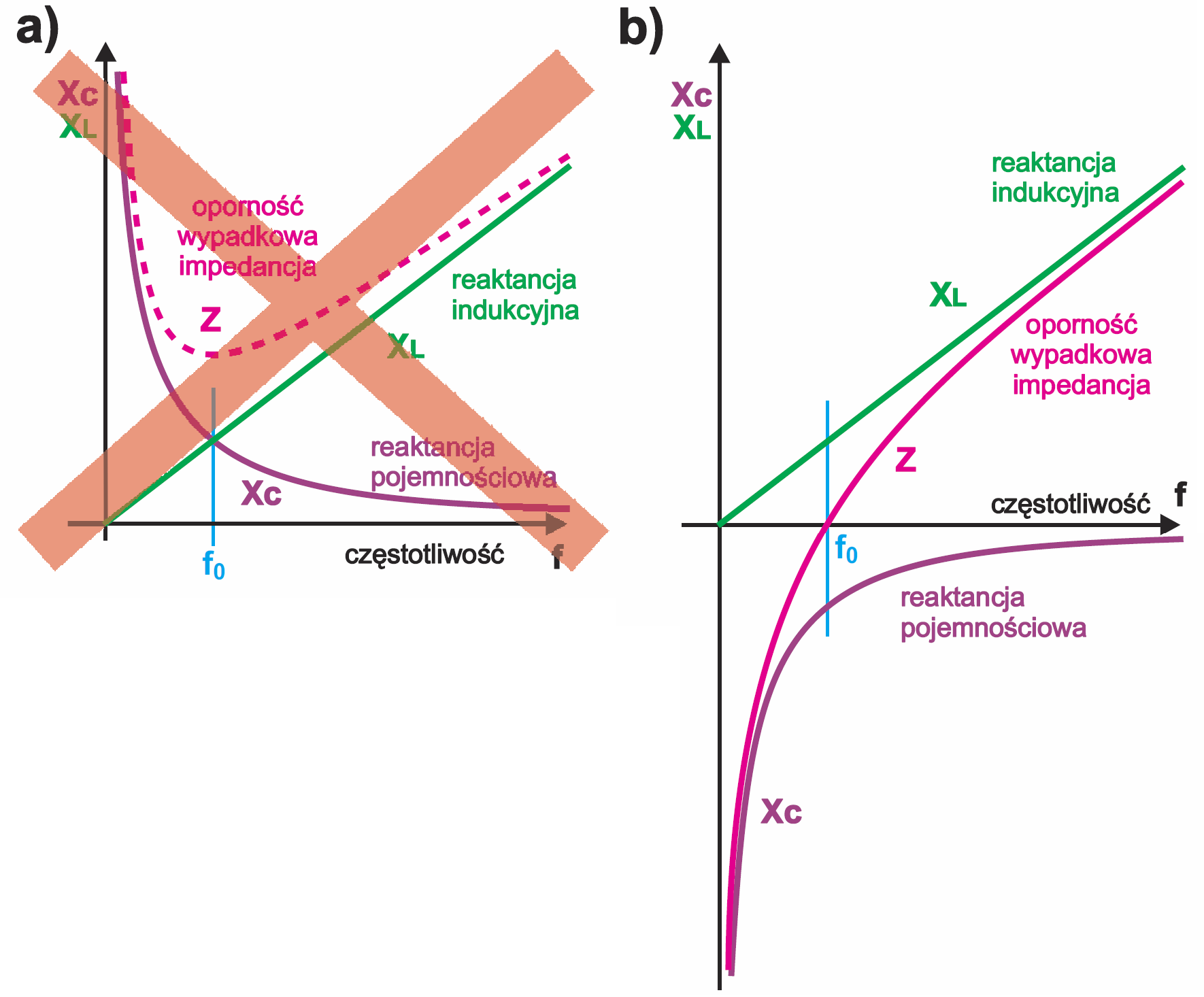
Reaktancje X_C, X_L zależą od częstotliwości. Moglibyśmy narysować na rysunku ich wartości w funkcji częstotliwości – rysunek 5a. Jeśli chcielibyśmy tak po prostu dodać wartości oporności, to wynikiem byłaby czerwona linia przerywana. W niektórych źródłach spotyka się podobne rysunki, ale jak wiemy z wcześniejszych rozważań, przy reaktancjach wypadkowa oporność nie jest zwyczajną sumą tych oporności wyrażonych w omach. W przypadku szeregowych obwodów RC i RL dodawaliśmy wektory. A jak pamiętamy, wektory reprezentujące reaktancję indukcyjną i pojemnościową są przeciwne. Rysunek 5a jest przekreślony, bo bardziej przeszkadza, niż pomaga zrozumieć problem, ponieważ nie uwzględnia przesunięcia fazowego między prądem a napięciem.

Jak wiemy, reaktancja pojemnościowa jest w pewnym sensie ujemna, „odwrotna”, „przeciwna” względem reaktancji indukcyjnej.

Ścisłe wzory na oporności różnią się znakiem, co moglibyśmy zapisać:

Z_L = jωL = jX_L

Z_C = –j1/ωC = –jX_C

Wypadkowa impedancja połączenia szeregowego jest sumą tych oporności, czyli:

Z = Z_L + Z_C = jX_L + (–jX_C)

Z = j(X_L – X_C)

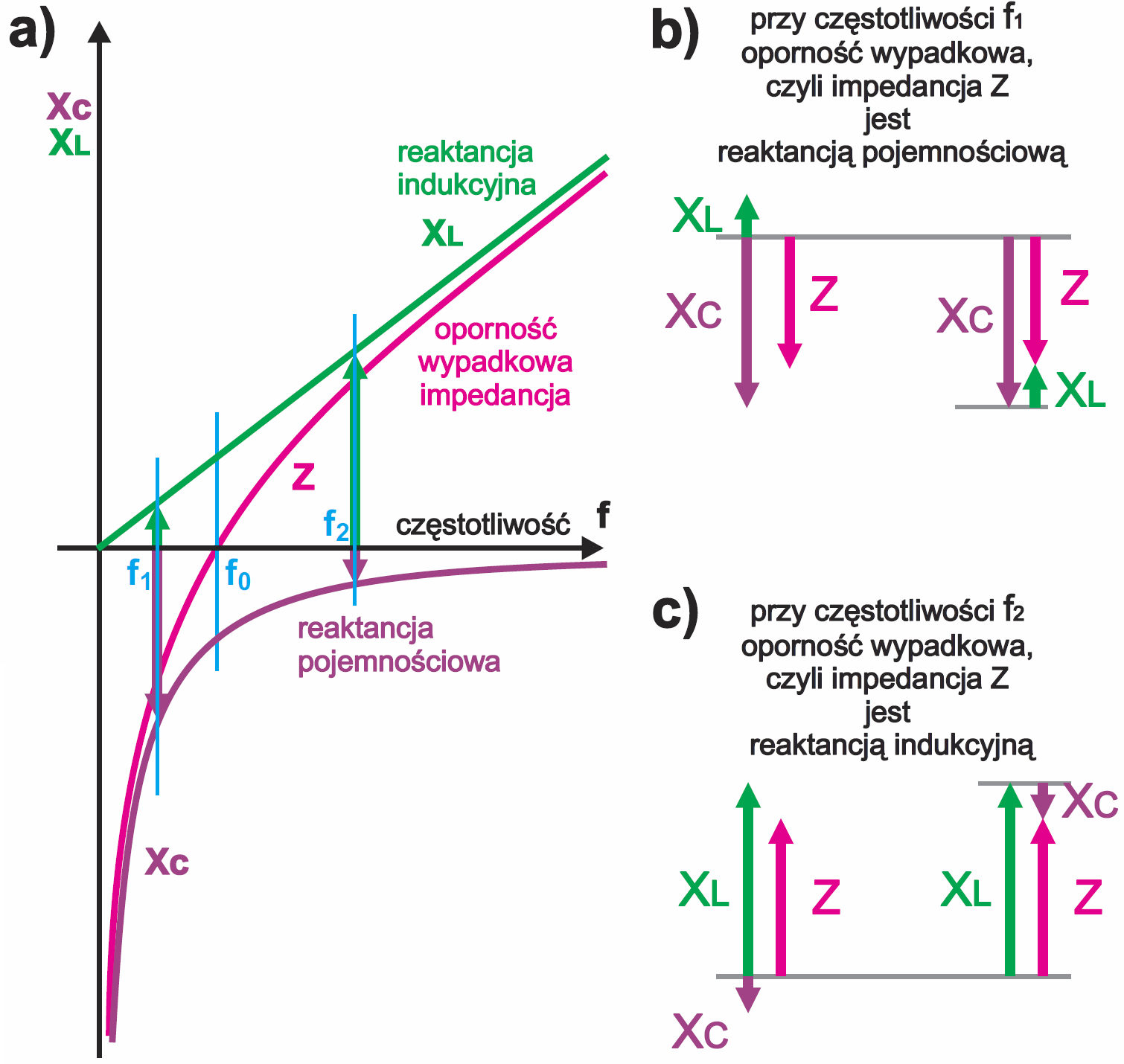
Reaktancje X_L i X_C jak najbardziej się sumują, ale ponieważ jedna z nich jest „ujemna”, więc ostatecznie ich liczbowe wartości się odejmują. Dlatego bardziej prawidłowe byłoby zobrazowanie reaktancji jak na rysunku 5b. Czerwona linia na rysunku 5b pokazuje sumę reaktancji cewki i kondensatora.

Warto też zobrazować to na wykresie wskazowym. Rysunek 6a świadczy, że przy małych częstotliwościach reaktancja X_L jest mała, a X_C – duża. Jak ilustruje przykład z rysunku 6b, przy małej częstotliwości f₁ szeregowy obwód rezonansowy LC z rysunku 4 zachowuje się jak kondensator (prąd wyprzedza napięcie o ćwierć okresu), ale my częściej mówimy, że obwód LC ma wtedy charakter pojemnościowy. Z kolei przy wielkich częstotliwościach reaktancja cewki X_L jest duża, a kondensatora X_C – mała. Wypadkowa impedancja Z ma wtedy charakter indukcyjny. Przy dużych częstotliwościach taki obwód zachowuje się jak cewka (prąd opóźnia się względem napięcia o ćwierć okresu) – przykład dla częstotliwości f₂ masz na rysunku 6c.

Nas jednak najbardziej interesuje przypadek szczególny, gdy X_L = X_C. Następuje to przy częstotliwości, którą nazywany częstotliwością rezonansową.

Możemy podstawić X_L = 2πfL, X_C = 1/2πfC i wyprowadzić znany wzór na częstotliwość rezonansową obwodu LC:

X_L=X_C

2πfL = 1/2πfC

(2πfL)(2πfC) = 1

(2π)²f²LC= 1

f²= 1/(2π)²LC

a stąd:

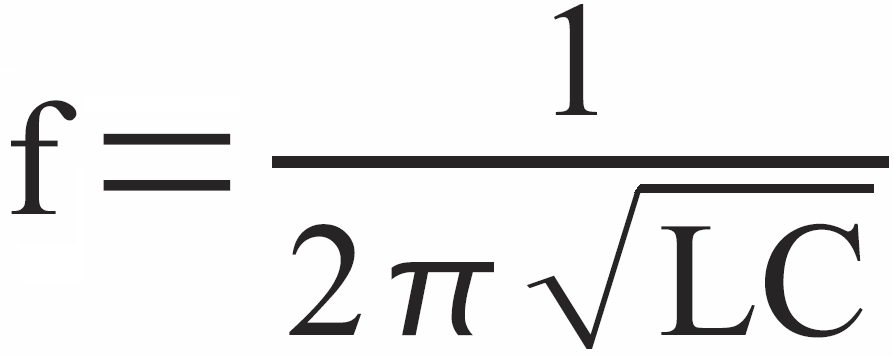
I właśnie przy częstotliwości rezonansowej, oznaczanej dość często f₀, mamy „osobliwość”. Mianowicie przy częstotliwości rezonansowej wypadkowa reaktancja szeregowego obwodu LC jest równa zeru!

Jeśli taki idealny obwód LC dołączylibyśmy do idealnego źródła napięcia sinusoidalnego według rysunku 4, to przy częstotliwości f₀ popłynąłby tam nieskończenie wielki prąd!

Oczywiście w praktyce tak nie będzie, bo prąd ograniczy choćby rezystancja uzwojenia cewki czy niezerowe rezystancje połączeń. Dlatego praktyczny obwód będzie dodatkowo zawierał szeregową rezystancję R_s, jak pokazuje rysunek 7. Znów szeregowa rezystancja R_s reprezentuje nie tylko rezystancję drutu, ale w ogóle wszelkie straty.

Nietrudno się domyślić, że i w tym przypadku wypadkowa oporność (impedancja) obwodu RLC jest równa sumie:

Z = R_s + Z_L + Z_C co ostatecznie daje: Z = R_s + j(X_L – X_C)

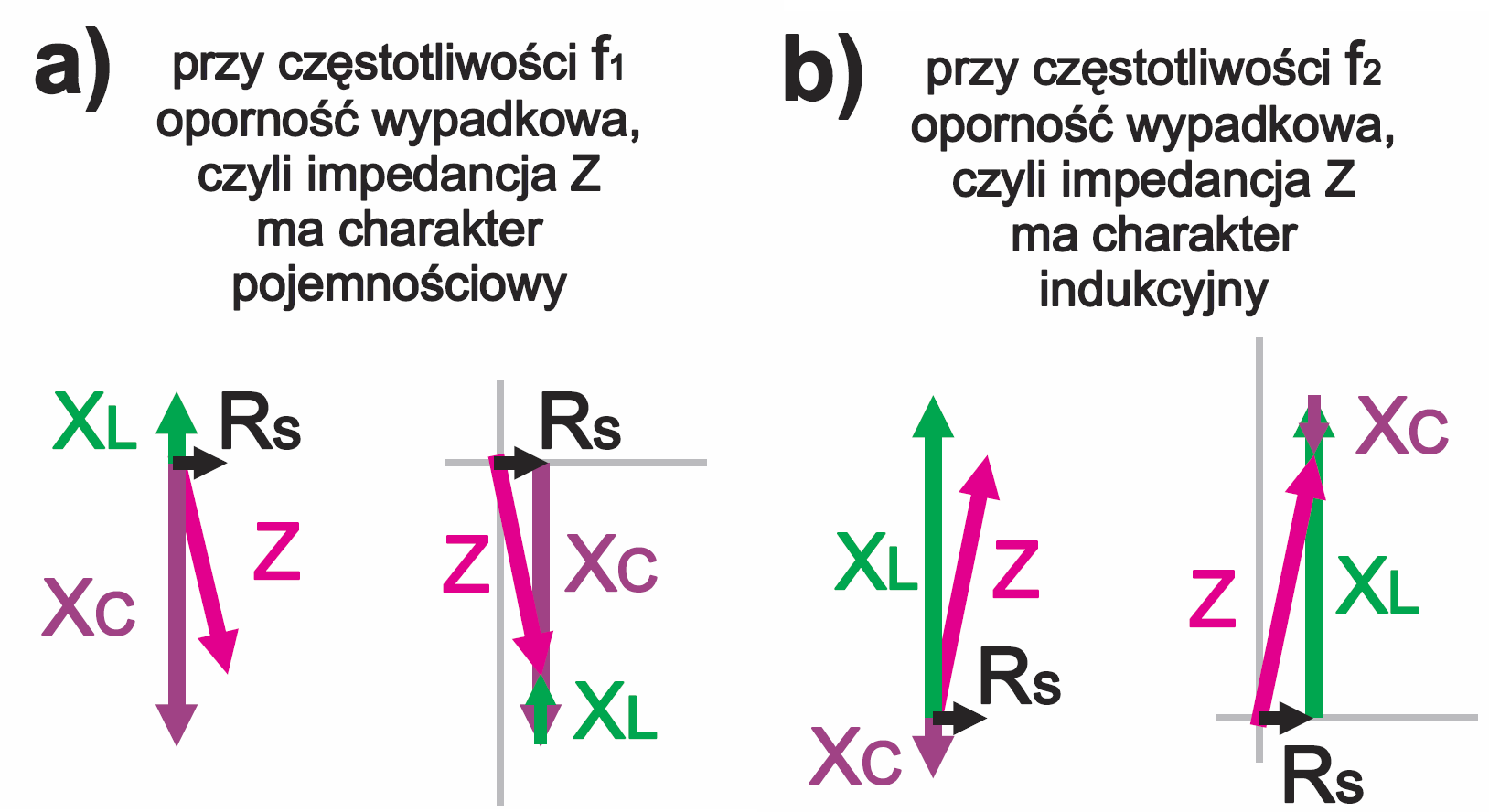
Znów trzeba brać pod uwagę zależności fazowe, więc trudno byłoby sensownie zaznaczyć rezystancję R_s na rysunku 5a czy 5b. Można natomiast łatwo zrobić to na wykresie wskazowym. Trzy przypadki pokazane są na rysunku 8, który dotyczy sytuacji z rysunku 6, tylko z dodatkową rezystancją strat R_s. Do obliczenia liczbowej wartości oporności wypadkowej, czyli modułu impedancji, można wykorzystać albo trójkąt Pitagorasa (|Z| = (R²+X²)^1/2), albo funkcje trygonometryczne.

Jeszcze raz podkreślam, iż przy częstotliwości rezonansowej f₀ reaktancje X_L, X_C są jednakowe i się znoszą. Nie ma przesunięcia fazy między prądem i napięciem, a wypadkowa oporność obwodu jest najmniejsza i równa R_s. Co ważne, całe napięcie zasilania występuje na rezystancji R_s.

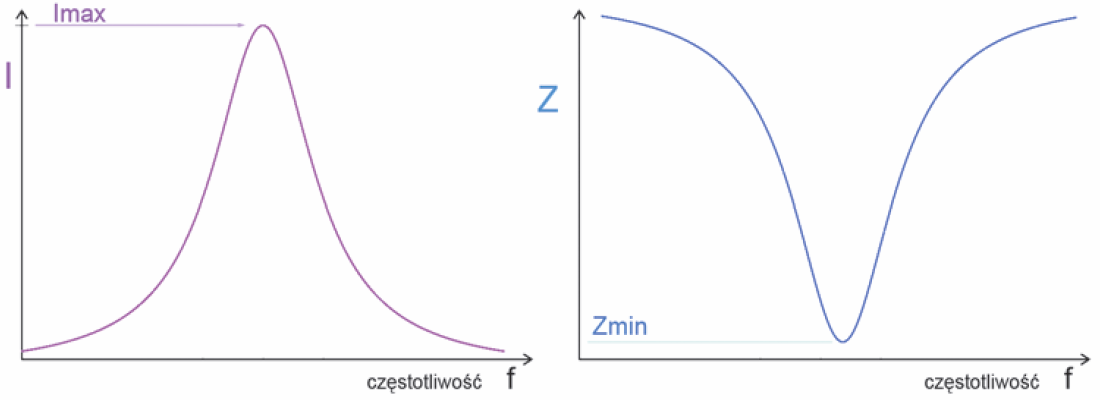
Często w podręcznikach przedstawia się zależność prądu i oporności wypadkowej od częstotliwości mniej więcej jak na rysunku 9.

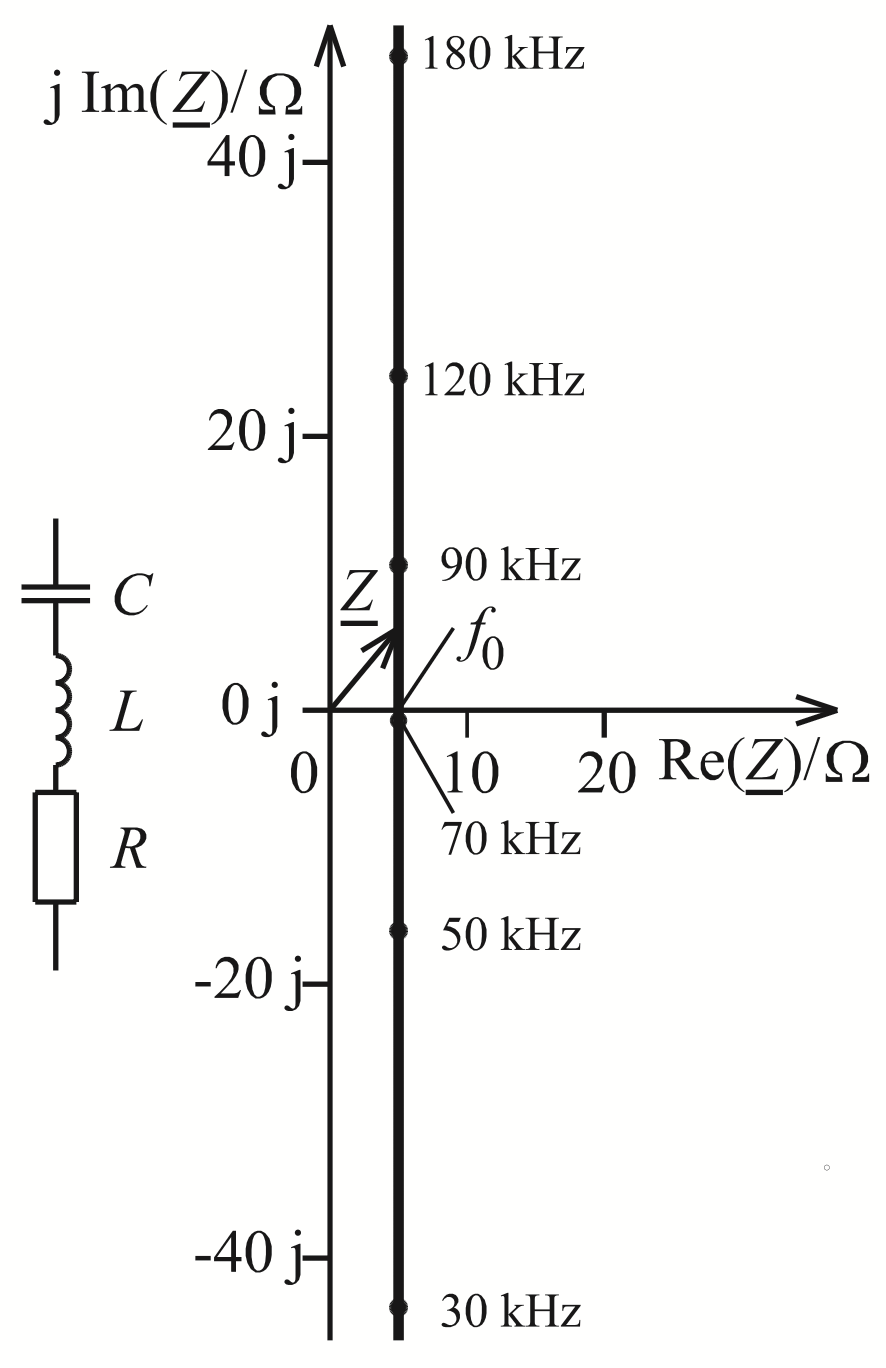
Pominiętą tu informację o kącie przesunięcia można zaznaczyć na oddzielnym wykresie. Rysunek 10 (z niemieckiej Wikipedii) w znacznie rzadziej spotykany sposób obrazuje przebieg impedancji, zaznaczony na płaszczyźnie zespolonej, gdzie można odczytać liczbową wartość (moduł impedancji – odległość od punktu zerowego) i kąt przesunięcia – dotyczy on szeregowego obwodu o parametrach: C = 0,1 μF, L = 50 uH, R = 5 Ω.

Moglibyśmy teraz badać związek szerokości krzywej z rysunku 9 z dobrocią Q. Ale na razie pomińmy ten wątek. Odnotujmy natomiast pewną ważną cechę, która ma ścisły związek z rezonansem i skutkami pokazanymi na fotografii 3. Otóż jak już wiemy, w stanie rezonansu impedancje X_L i X_C znoszą się i całe napięcie generatora (U_G) występuje na rezystancji R_s. Widziana z zewnątrz wypadkowa oporność obwodu RLC jest równa R_s i w obwodzie płynie największy prąd (I = U_G/R_s).

Chyba nie masz wątpliwości, że całe napięcie źródła U_G występuje wtedy na rezystancji R_s? Ale co z napięciami na cewce i kondensatorze?

Otóż napięcia na cewce i kondensatorze będą dużo większe niż napięcie zasilające! Skąd się wezmą?

Ano właśnie tak daje o sobie znać zjawisko rezonansu. Ale nie znaczy to, że w rezonansie są złamane podstawowe prawa fizyki i że napięcie „pojawia się znikąd”. Wprost przeciwnie, wszystko wynika z elementarnych zasad i wzorów, które dobrze znasz.

Otóż jak w każdym obwodzie szeregowym, ten sam prąd I płynie przez wszystkie elementy i wywołuje na nich napięcia (spadki napięć). Nadal obowiązuje tu napięciowe prawo Kirchhoffa: suma napięć na elementach równa jest napięciu źródła: U_G = U_L+U_Rs+U_C

Nadal, także przy rezonansie, obowiązuje prawo Ohma – fundamentalna zależność między napięciem, prądem i opornością. Jak już ustaliliśmy, całe napięcie generatora występuje na rezystancji R_s, co możemy zapisać U_Rs=I×R_s. Prąd I, przepływając przez reaktancje, najzwyczajniej wywołuje na nich (spadki) napięcia U_L=I×X_L, UC=I×X_C.

Znajdźmy w prosty sposób wartości tych napięć w zależności od dobroci Q. Nieprzypadkowo wcześniej zdefiniowaliśmy dobroć obwodu LC jako:

Q = X_L/R_s = X_C/R_s = ρ/R_s = (L/C)^1/2/R_s

Oznacza to, że reaktancje X_L, X_C są Q-krotnie większe od R_s. A jeśli tak, to prąd I, przepływając przez Q-krotnie większe oporności, wywoła na nich napięcia U_L i U_C także Q-krotnie większe od napięcia na R_s – proste i oczywiste! A ponieważ U_Rs=U_G, więc w szeregowym obwodzie rezonansowym napięcia na kondensatorze i cewce są Q-krotnie większe od napięcia zasilania:

U_L = U_C = Q × U_G

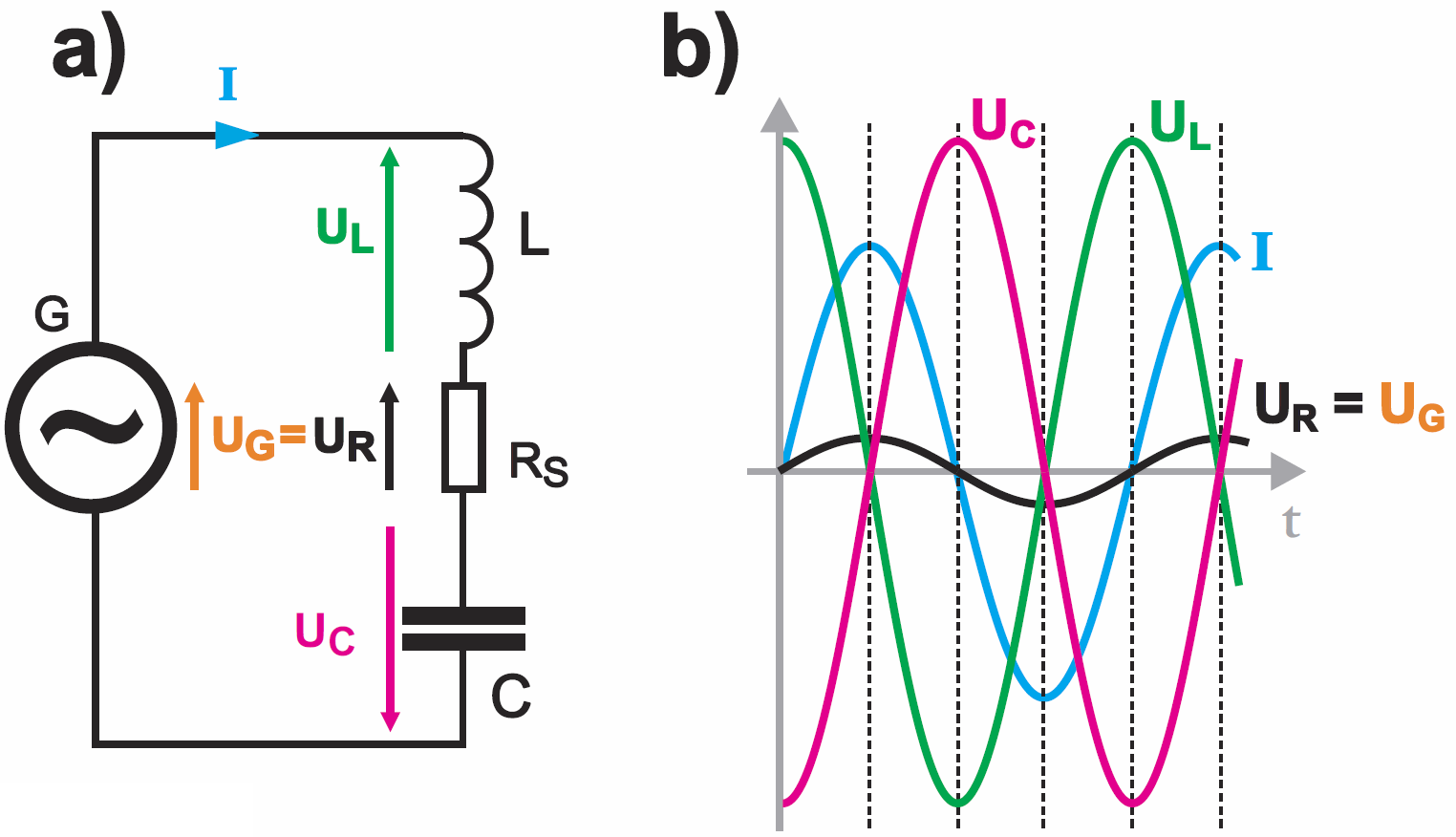
Oczywiście wartości tych wysokich napięć są równe, a przebiegi napięcia mają przeciwne fazy, więc się znoszą. Rysunek 11 pokazuje prąd i napięcia w stanie rezonansu dla obwodu RLC o dobroci Q = 10.

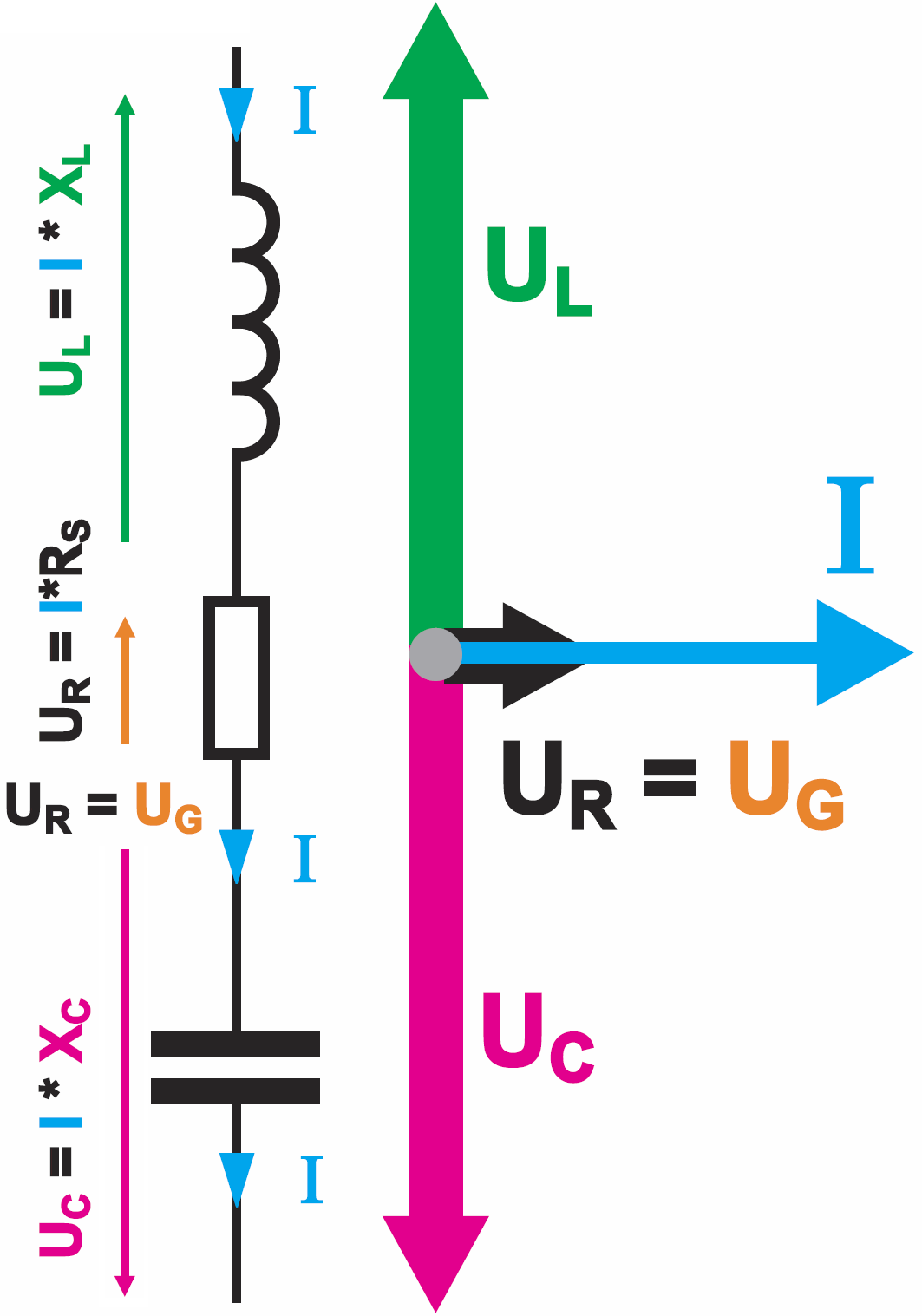
Natomiast na rysunku 12 pokazany jest odpowiedni wykres wektorowy. W praktycznych obwodach dobroć może wynosić nawet kilkaset, więc napięcia rezonansowe ( przepięcia ) na cewce i kondensatorze mogą być kilkaset razy większe od napięcia zasilającego taki obwód.

Czym większa dobroć, tym większe przepięcia. Z takiej analizy wynika, iż gdy R_s maleje do zera, czyli gdy rośnie dobroć Q, to wtedy rośnie zarówno prąd I, jak też napięcia na cewce i kondensatorze. Teoretycznie rosłyby one do nieskończoności…

Totalna destrukcja?

Niektórym początkującym nie bardzo mieści się to w głowie, że w rzeczywistym szeregowym obwodzie LC mogą się pojawić napięcia wielokrotnie większe od napięcia zasilania. U innych początkujących jest odwrotnie: na hasło rezonans przypomina się most z fotografii 3 i pojawia się przerażająca perspektywa totalnej destrukcji obwodu LC. Niektórym wydaje się, że podobnie jak w przypadku mostu z Angers, nawet małe źródło może stopniowo „napompować” obwód LC i stopniowo zwiększać drgania niemal w nieskończoność, doprowadzając do katastrofy. Na myśl przychodzi też groźny przykład dziecka, które może stopniowo tak bardzo rozkołysać huśtawkę, że zabawa skończy się tragedią – fotografia 13 z Wikipedii.

Istotnie, huśtawka taka jest dobrą analogią obwodu rezonansowego RLC i rzeczywiście w pewnych szczególnych przypadkach wysokie napięcie rezonansowe może doprowadzić w obwodach LC choćby do uszkodzenia (przebicia) kondensatora zbyt wysokim napięciem. Ma to praktyczne znaczenie na przykład w nadajnikach radiowych (np. krótkofalarskich).

Jednak ogólnie biorąc, szeregowe obwody rezonansowe nie współpracują bezpośrednio z idealnym źródłem sygnału i nie ma możliwości „stopniowego napompowania” obwodu LC.

Owszem, w idealnym przypadku (rysunek 4) prąd podczas rezonansu wzrósłby do nieskończenie wielkiej wartości, podobnie do nieskończoności wzrosłyby wtedy napięcia na cewce i kondensatorze. Jednak w rzeczywistych warunkach nigdy to nie nastąpi, choćby z uwagi na ograniczoną wydajność prądową źródła sygnału (generatora). To właśnie głównie z uwagi na właściwości źródła sygnału wymuszającego, prąd podczas rezonansu nie może więc rosnąć ani do nieskończoności, ani nawet do bardzo dużych wartości.

Nie ma też możliwości „stopniowego napompowania” szeregowego obwodu LC energią, ponieważ oznaczałoby to zwiększanie prądu, a na to nie pozwoli generator.

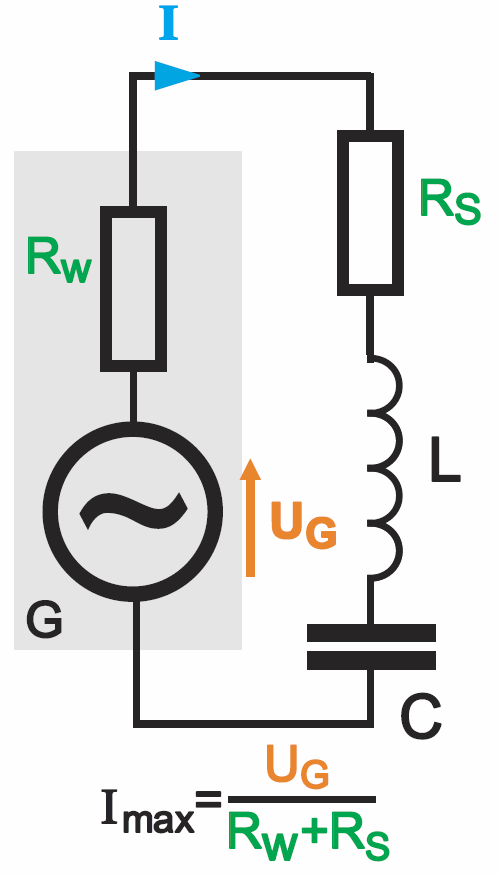
Prąd wzrośnie jedynie do jakiejś wartości I_max, wyznaczonej nie tylko przez rezystancję strat R_s obwodu rezonansowego, ale też przez rezystancję wewnętrzną źródła sygnału – rysunek 14.

A tym samym napięcia na cewce i kondensatorze podczas rezonansu nie będą rosnąć dowolnie, a jedynie do jakiejś wartości określonej elementarnym wzorem:

U_max = I_max × X_L= I_max × X_C = I_max × ρ = I_max × (L/C)^1/2

Zapamiętaj, że ostatecznie o wielkości przepięć U_L=I×X_L, U_C=I×X_C decyduje prąd płynący w obwodzie, a nie tylko szeregowa rezystancja strat i dobroć Q. A w praktyce prąd ten zależy nie tylko od rezystancji szeregowej R_s, ale też od właściwości źródła sygnału. Tylko w szkolnych i akademickich ćwiczeniach dotyczących obwodu szeregowego RLC pomija się ograniczenia wnoszone przez źródło sygnału, a rezystancję R_s traktuje jako wielkość niezależną (często jest to rezystor, na którym mierzy się napięcie, które jest wprost proporcjonalne do płynącego tam prądu). W efekcie szkolne rozważania, a nawet pomiary takich obwodów RLC niewiele mają wspólnego z praktyką.

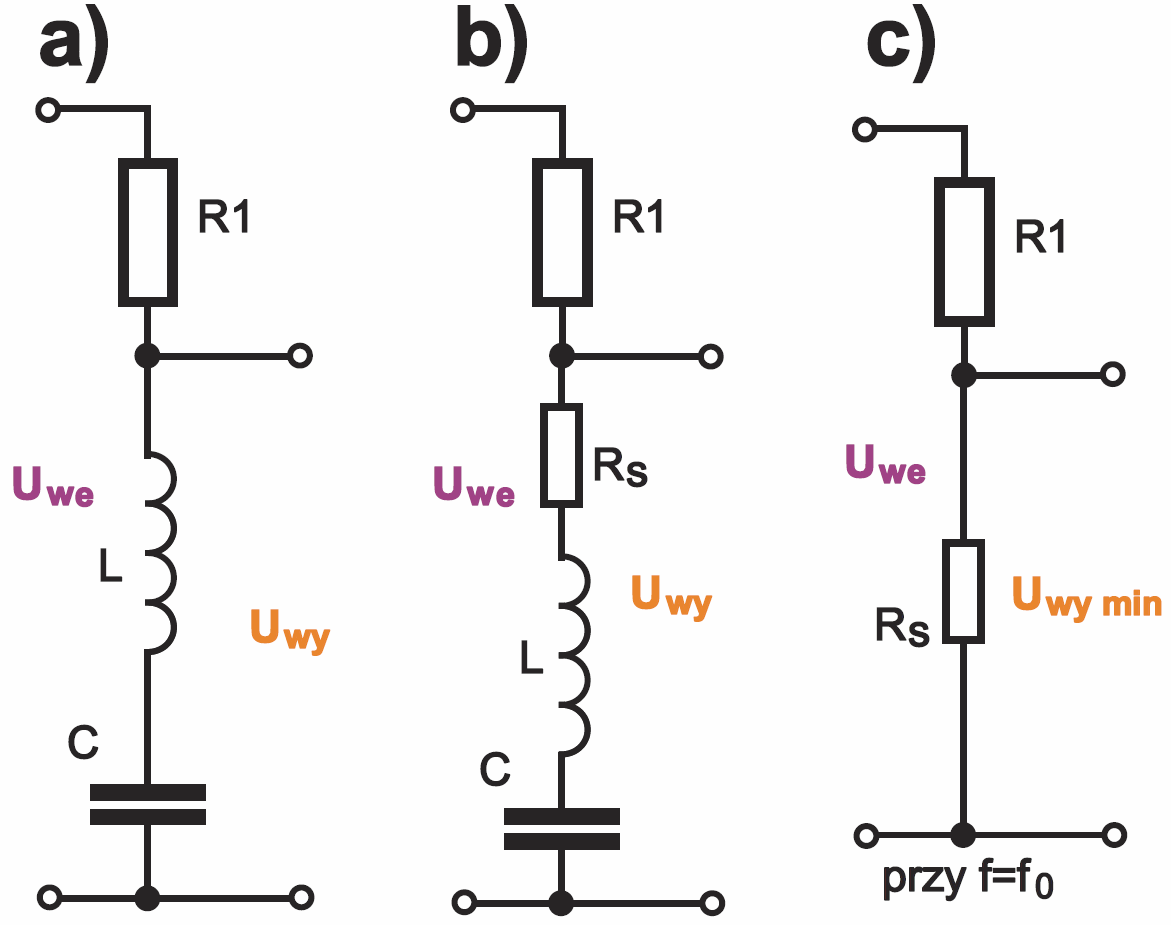
W praktyce szeregowe obwody rezonansowe są wykorzystywane głównie jako pułapki. Czyli nie służą do wydzielania użytecznych, tylko do tłumienia niepożądanych składników sygnału. W uproszczeniu wygląda to jak na rysunku 15a. Najogólniej biorąc, sygnały o częstotliwości rezonansowej są zwierane do masy. Ale nie całkowicie! Pomimo podobieństw, nie jest to szkolny obwód RLC, natomiast chodzi o dzielnik napięcia, stworzony z zewnętrznej rezystancji R1 i właściwego obwodu RLC, który jest elementem dzielnika, jak ilustruje rysunek 15b. Wtedy tłumienie maksymalne dla częstotliwości rezonansowej będzie wyznaczone przez stosunek rezystancji R1 i R_s, jak pokazuje rysunek 15c. Należałoby więc badać nie tyle prądy, co stosunek oporności wypadkowej obwodu R_s, L, C do rezystancji R1. A takich ćwiczeń w szkole i na uczelniach raczej się nie przeprowadza.

Trzeba jednak przyznać, że w związku z powszechną cyfryzacją, filtry zawierające szeregowe obwody rezonansowe LC są wykorzystywane coraz rzadziej. Dlatego w dalsze szczegóły nie będziemy się wgłębiać. Dla praktyków większe znaczenie mają równoległe obwody rezonansowe LC, którymi zajmiemy się w następnym odcinku.

Piotr Górecki