Elektronika (nie tylko) dla informatyków (9) Oporność zespolona, czyli w poszukiwaniu liczb zespolonych

Mam nadzieję, że rozważania dotyczące przedstawiania napięć i prądów w postaci wektorów omówione w poprzednim wykładzie są dla Ciebie jasne. Jeśli nie, koniecznie wróć do poprzednich odcinków, analizuj je, szukaj dodatkowych informacji. Omawiamy bowiem fundamentalne, bardzo ważne zagadnienia, które obowiązkowo trzeba sobie przyswoić.

W sumie idea jest prosta: długość wektora reprezentuje wartość prądu lub napięcia, a kąt wektora reprezentuje przesunięcie fazy między napięciem i prądem. Dotychczas w postaci wektorów zaznaczaliśmy napięcia i prądy sinusoidalne.

A co byś powiedział, gdybyśmy w postaci wektorów zaznaczali nie tylko prądy i napięcia, ale też oporności R oraz X_c?
Tak! Oporności w postaci wektorów! Wracamy więc do rysunku 4 oraz rysunków 11…13 zamieszczonych w poprzednim wykładzie.

Oporność zespolona – impedancja

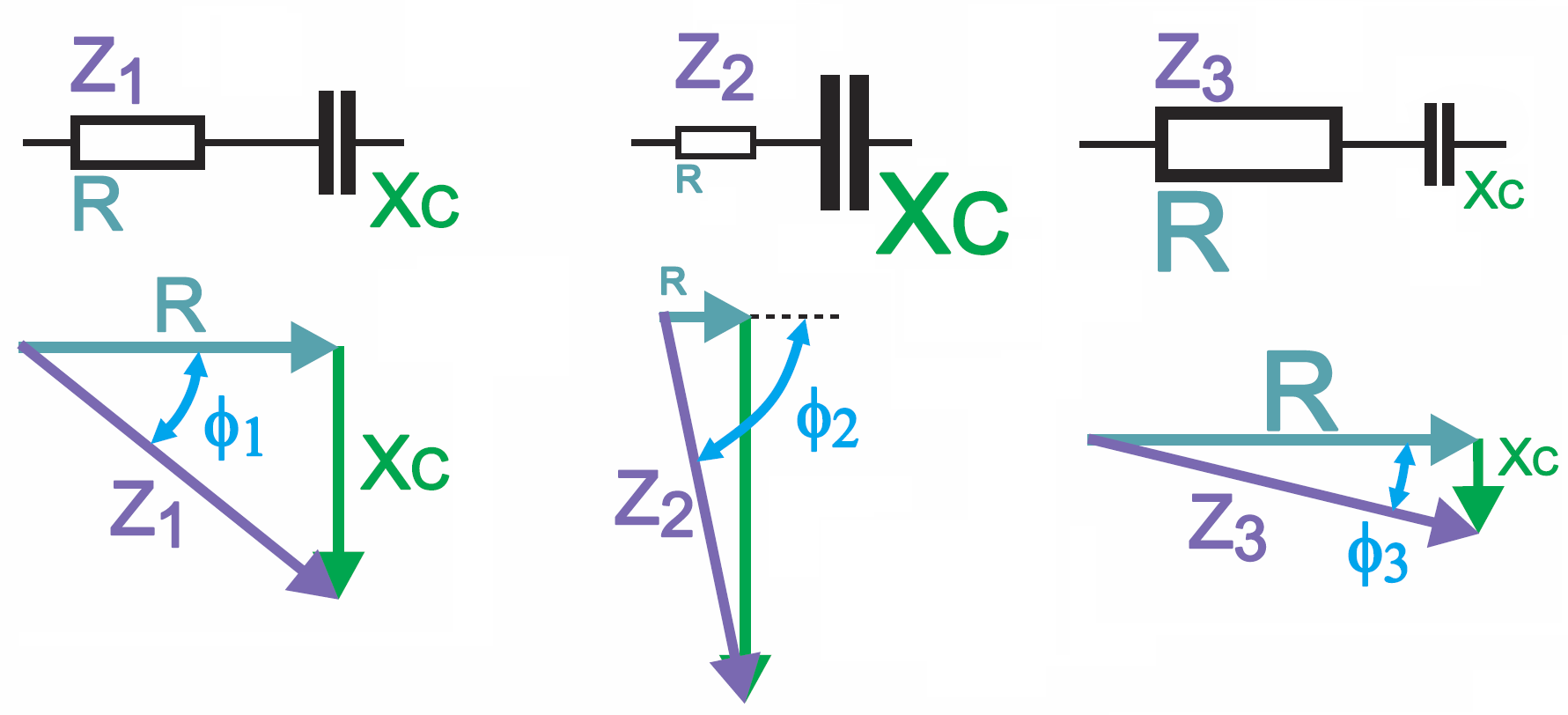
Idea znów jest beznadziejnie prosta i zgodna z intuicją. Długość wektorów odpowiada liczbowej wartości R i X_c – to jest oczywiste. Ponieważ w rezystancji kąt przesunięcia między napięciem i prądem wynosi 0, więc wektor rezystancji rysujemy poziomo, zgodnie z dodatnim zwrotem osi liczbowej. Natomiast kąt przesunięcia w reaktancji wynosi 90 stopni (π/2 radiana), więc wektor reaktancji narysujemy pionowo. Tylko czy pionowo w górę, czy pionowo w dół?

Wektor reaktancji pojemnościowej X_c narysujemy pionowo w dół!

Jeśli masz wątpliwości, poprzedniego odcinka, a zwłaszcza rysunki 6…13. Nieprzypadkowo wcześniej tak dużo uwagi poświęciłem wektorom prądu (tego samego dla R i C) i napięć. Oporności omawiane na rysunkach 11…13 (poprzedni wykład) możemy przedstawić na rysunku 1.

Teraz wektory nie reprezentują już napięć, tylko właśnie oporności. W szeregowym obwodzie RC istotnie dodajemy oporności – ale dodajemy je wektorowo, zgodnie z regułami znanymi z matematyki. Wypadkowy „ukośny” wektor reprezentuje oporność wypadkową – impedancję.

Zauważ, że takie zobrazowanie ma bardzo mocne uzasadnienie na wcześniejszych rysunkach. W sumie zgadza się też z intuicją: długość wektora to „liczbowa wartość oporności wypadkowej”, a fachowo: moduł impedancji, natomiast kąt, nazywany czasem argumentem impedancji, reprezentuje przesuniecie (różnicę) fazy napięcia względem prądu w tej zespolonej oporności.

Wprowadzając pojęcie impedancji, rozszerzamy pojęcie rezystancji, która wcześniej była wykorzystywana tylko w obwodach prądu stałego. Teraz impedancję możemy wykorzystywać także do obliczeń przy przebiegach zmiennych. Ale czy pamiętasz, że reaktancja pojemnościowa X_c ma sens tylko przy przebiegach sinusoidalnych? W związku z tym także impedancja ma sens tylko przy przebiegach sinusoidalnych. Teraz, po wprowadzeniu pojęcia impedancji, możemy dla przebiegów sinusoidalnie zmiennych korzystać z prawa Ohma i wzorów:

I = U / Z       U = I × Z       Z = U / I

Powinieneś jednak mieć świadomość, że jeśli za Z podstawisz moduł impedancji, to takie obliczenia są uproszczone, ponieważ kąt przesunięcia fazy jest uwzględniony co najwyżej „częściowo”. Do tej ważnej sprawy jeszcze wrócimy.

Mam nadzieję, że dotychczasowe rozważania nie były zbyt trudne i że bez problemu zaakceptujesz propozycję przedstawiania w postaci wektorów nie tylko napięć i prądów, ale też oporności. Zapamiętaj raz na zawsze, że tę dziwną oporność wypadkową nazywamy impedancją i oznaczamy literą Z.

Celowo do tej pory używałem nieprecyzyjnego określenia „oporność”. Teraz zaczynamy zagadnienie uściślać. Impedancja to ogólne, szerokie pojęcie – to oporność wypadkowa. Natomiast rezystancja to przypadek szczególny impedancji, podobnie jak przypadkiem szczególnym jest reaktancja pojemnościowa. Słusznie możemy powiedzieć i zapisać, że impedancja rezystora jest równa jego rezystancji:

Z = R

podobnie jest dla kondensatora – impedancja jest równa jego reaktancji:

Z = X_c

Są jeszcze inne szczególne przypadki – powrócimy do nich przy omawianiu indukcyjności i reaktancji indukcyjnej. Ja na przykładzie szeregowego obwodu RC chciałem możliwie najprościej wytłumaczyć Ci pojęcie impedancji, jako „uniwersalnej oporności”. Jednak impedancja to nie tylko szeregowe połączenie R i C. Ponadto dobrze byłoby, żeby rezystancja nie kojarzyła Ci się z opornikiem. Raczej niech rezystancja kojarzy Ci się z zerowym przesunięciem fazy.

W sumie temat jest szeroki i będziesz się weń wgryzać stopniowo. Już na początku zapamiętaj, że impedancja danego obwodu zazwyczaj nie jest stała, tylko zmienia się w funkcji częstotliwości. Nic dziwnego, ponieważ w funkcji częstotliwości zmienia się składowa reaktancyjna X_c. Impedancja nie zależy od częstotliwości tylko wtedy, gdy jest czystą rezystancją, czyli gdy Z = R.

Elementarne, uproszczone obliczenia

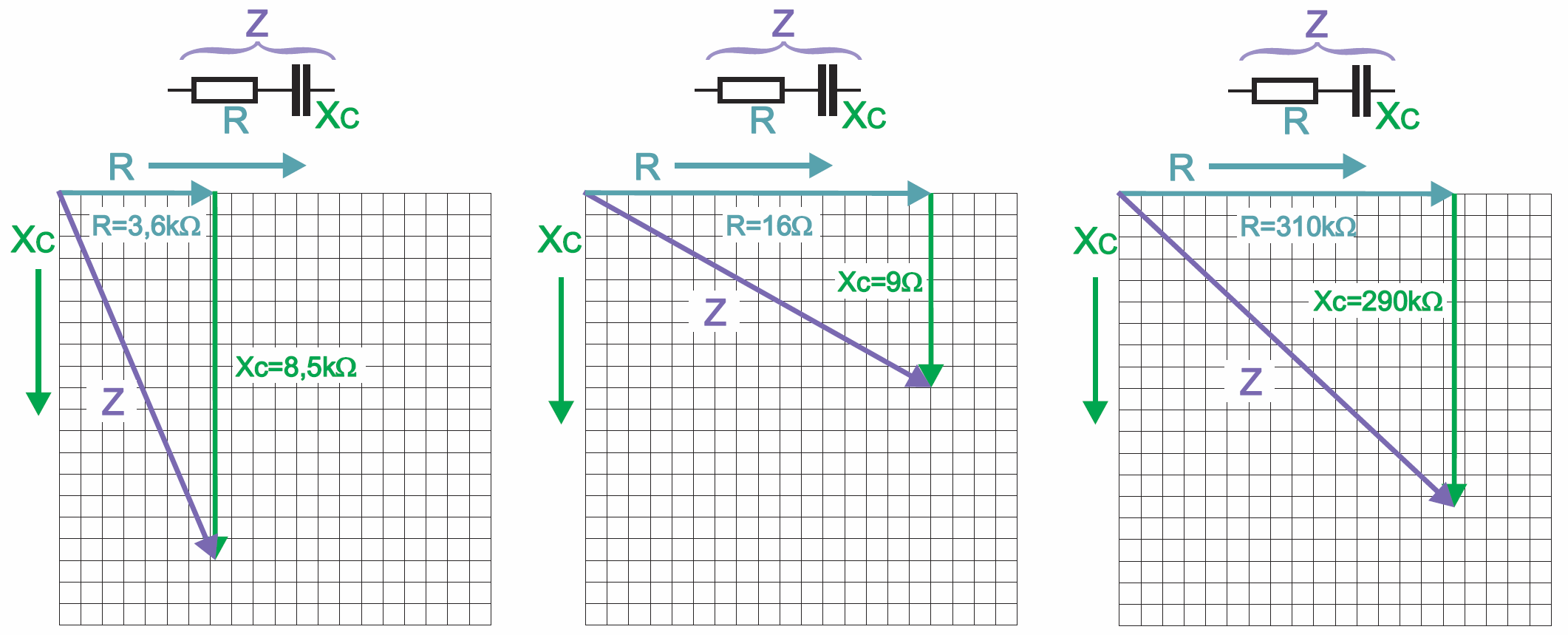
Na razie, w przypadku szeregowego połączenia rezystora i kondensatora, nauczyliśmy się za pomocą prościutkiej metody graficznej prawidłowo określić oporność wypadkową, czyli impedancję Z. Do takich obliczeń wystarczy kawałek kartki w kratkę i linijka. Długość wektora reprezentuje wartość oporności. Składową rezystancyjną (R) zaznaczamy jako poziomy wektor skierowany w prawo. Składową pojemnościową (reaktancję X_c) przedstawiamy wektorem skierowanym w dół. Rysunek 2 pokazuje trzy przykłady takich obliczeń, wykorzystujące różne skale. Długość fioletowego wektora wypadkowego reprezentuje wyrażoną w omach „oporność wypadkową”, którą oznaczamy literą Z i nazywamy impedancją. Przy okazji kąt φ wskazuje przesunięcie fazowe między napięciem i prądem w takim obwodzie.

Kto chce, może wartość impedancji obliczyć, i to kilkoma metodami. Zauważ, że zawsze mamy tu do czynienia z trójkątem prostokątnym, a więc można skorzystać z twierdzenia Pitagorasa:

Z²= R²+ Xc². A stąd:

Korzystając z twierdzenia Pitagorasa, obliczamy jedynie moduł impedancji, ale nie mamy informacji o fazie. Pełne informacje uzyskalibyśmy, korzystając z funkcji trygonometrycznych, jednak na razie do pełnego obrazu zagadnienia brakuje nam pewnego istotnego szczegółu i nie będziemy w to wchodzić.

Proste metody kartki w kratkę i linijki oraz wykorzystanie twierdzenia Pitagorasa, z powodzeniem mogą być wykorzystywane w praktyce, ponieważ w elektronice nie zawsze potrzebna jest dokładna informacja o fazie i zazwyczaj nie musimy przeprowadzać precyzyjnych obliczeń. Choć w praktyce takie metody wykorzystywane są rzadko, spróbuj przeprowadzić kilka tego rodzaju ćwiczeń rachunkowych i na kartce.

A teraz kolejny ważny szczegół praktyczny. Zwróć uwagę, że często w ogóle nie ma potrzeby przeprowadzania obliczeń! Mianowicie gdy któraś z oporności składowych jest co najmniej 3 razy większa od drugiej, wtedy oporność wypadkowa będzie praktycznie równa tej większej oporności składowej. Korzystając z twierdzenia Pitagorasa, obliczmy na przykład impedancję Z szeregowego połączenia R i C, gdy R=1 kΩ, X_c=3 kΩ:

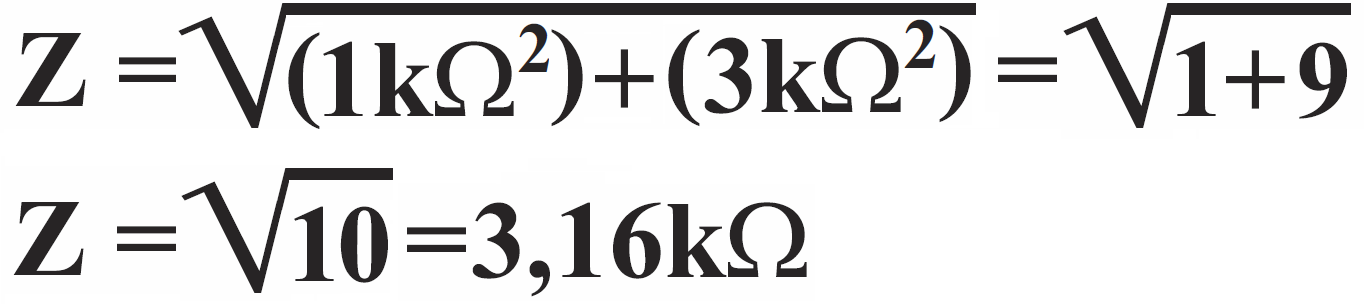
Zauważ, że obliczona wartość Z=3,16 kΩ jest większa od X_c=3 kΩ tylko o 5,4%, co ilustruje rysunek 3a. Gdyby któraś z oporności była 4 razy większa, na przykład R=4 kΩ, X_c=1 kΩ, wtedy Z=4,12 kΩ, czyli tylko o 3% więcej niż R=4 kΩ – patrz rysunek 3b. Przy pięciokrotnej różnicy oporności składowych, impedancja jest tyko o 2% większa od większego składnika – przykład masz na rysunku 3c.

Zapamiętaj, że przy dużej różnicy wartości oporności składowych, oporność wypadkowa jest zbliżona do większego ze składników; podobnie kąt przesunięcia jest określony przez dominujący składnik. Ponadto w elektronice powszechnie stosujemy rezystory o tolerancji 5% oraz kondensatory o tolerancji 10%, 20%, a nawet jeszcze gorszej, więc precyzyjne obliczenia często nie mają sensu.

Nie takie to proste…

A teraz chciałbym Ci zwrócić uwagę na dwa problemy. Oto pierwszy: zauważ, że na rysunkach 11…13 w poprzednim wykładzie wielkość napięcia U_G, reprezentowana przez fioletowy wektor, jest niezmienna – to akurat jest oczywiste, bo zgodnie z rysunkiem 4 (poprzedni wykład) chodzi o napięcie z generatora. Nieprzypadkowo jednak dobrałem takie wartości, żeby w każdym przypadku prąd I, reprezentowany przez czerwony wektor, miał taką samą wartość. Oznacza to, że w każdym przypadku z rysunków 11…12 i 13 (poprzedni wykład) liczbowa wartość impedancji Z jest jednakowa. Ściślej: moduł impedancji jest jednakowy! A przecież nie mają one identycznych wartości, ponieważ różnią się kątem przesunięcia fazy napięcia względem prądu. I właśnie tu jest problem: jak matematycznie zapisać wartość impedancji Z, żeby uwzględnić nie tylko moduł, ale też kąt przesunięcia? I jak potem przeprowadzać obliczenia? Do tej ważnej sprawy jeszcze wrócimy, a teraz omówmy drugi kluczowy problem.

Otóż okazało się, że potrafimy w prosty sposób obliczać oporność wypadkową przez dodawanie wektorów składowych, których długość reprezentuje oporność w omach, natomiast kąt wskazuje na przesunięcie fazy, jakie występuje między napięciem a prądem. Niestety, metoda graficzna jest o tyle ułomna, że pozwala w prosty sposób określać oporność wypadkową jedynie przy połączeniu szeregowym, gdy oporności dodajemy.

A jak „ugryźć” problem, gdy mamy połączenie równoległe?

W przypadku rezystorów radzimy sobie z tym dość łatwo, bo mamy wzór na oporność wypadkową:

a w przypadku dwóch rezystorów:

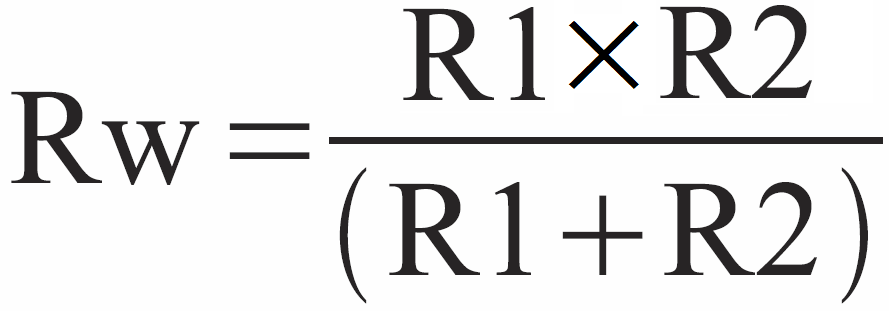
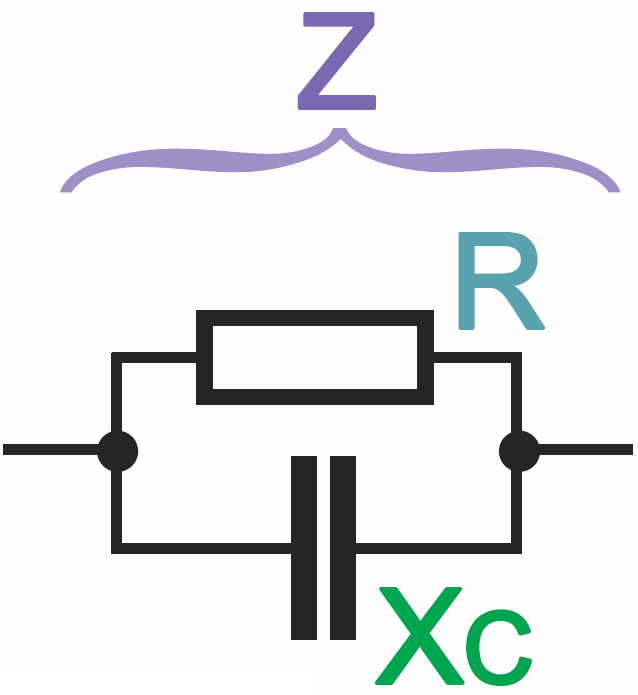
A jak liczyć impedancję Z, gdy w grę wchodzą reaktancje? Jak na przykład policzyć czy choćby zapisać impedancję równoległego połączenia R i C, czyli dwójnika z rysunku 4?

Tym razem nie możemy zsumować wektorów rezystancji i reaktancji. Także teraz proste podstawienie liczbowych wartości do zależności R × X_c / (R + X_c) da błędny wynik. A przecież oprócz połączenia równoległego R i C w grę wchodzą też znacznie bardziej skomplikowane przypadki. Dodawanie wektorów znakomicie pomogło zrozumieć zasadniczą ideę, związaną z przesunięciem fazy, ale w trudniejszych przypadkach niewiele pomaga. Należałoby bowiem wektory mnożyć, dzielić i poddawać jeszcze bardziej złożonym operacjom matematycznym. Zapewne domyślasz się, że nie byłoby to proste, choć jest możliwe.

Przydałby się jakiś inny, prostszy i uniwersalny sposób.

Okazuje się, że taki sposób istnieje. I znów podstawowa idea jest beznadziejnie prosta: można korzystać z tych samych wzorów, co przy prądzie stałym, jednak do obliczeń trzeba wziąć prawidłowo zapisaną „pełną” wartość impedancji Z, a nie tylko moduł impedancji. Potrzebny jest sposób zapisania reaktancji i impedancji, uwzględniający nie tylko „wartość liczbową”, czyli moduł, ale też kąt przesunięcia.

Nie zdziwię się, jeżeli zaproponujesz zapis impedancji Z w postaci dwóch liczb: modułu i kąta przesunięcia, albo też dwóch składowych: rezystancyjnej i reaktancyjnej, co sugerowałyby wcześniejsze rysunki 4…13 w poprzednim wykładzie oraz rysunki 1 i 2 w tym odcinku. Owszem, można by tak robić, ale jeśli chcemy przeprowadzać obliczenia i wykorzystywać wszystkie znane wzory, przydałby się zapis impedancji za pomocą jednej liczby. I tu dochodzimy do kluczowego momentu naszych rozważań.

Jedna liczba?

Warto byłoby wiedzieć, dlaczego szukamy jednej liczby do „pełnego” wyrażenia X_c (a także Z)? Otóż wtedy moglibyśmy korzystać ze wszystkich zależności i wzorów, które do tej pory stosowaliśmy tylko w obwodach prądu stałego.

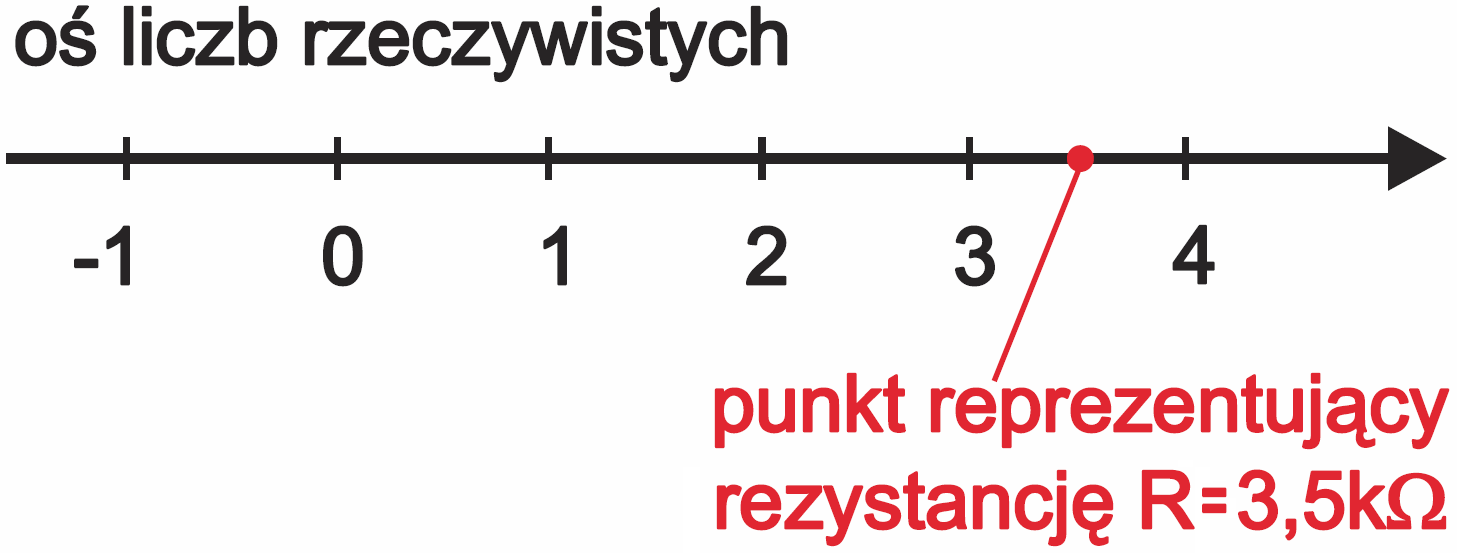
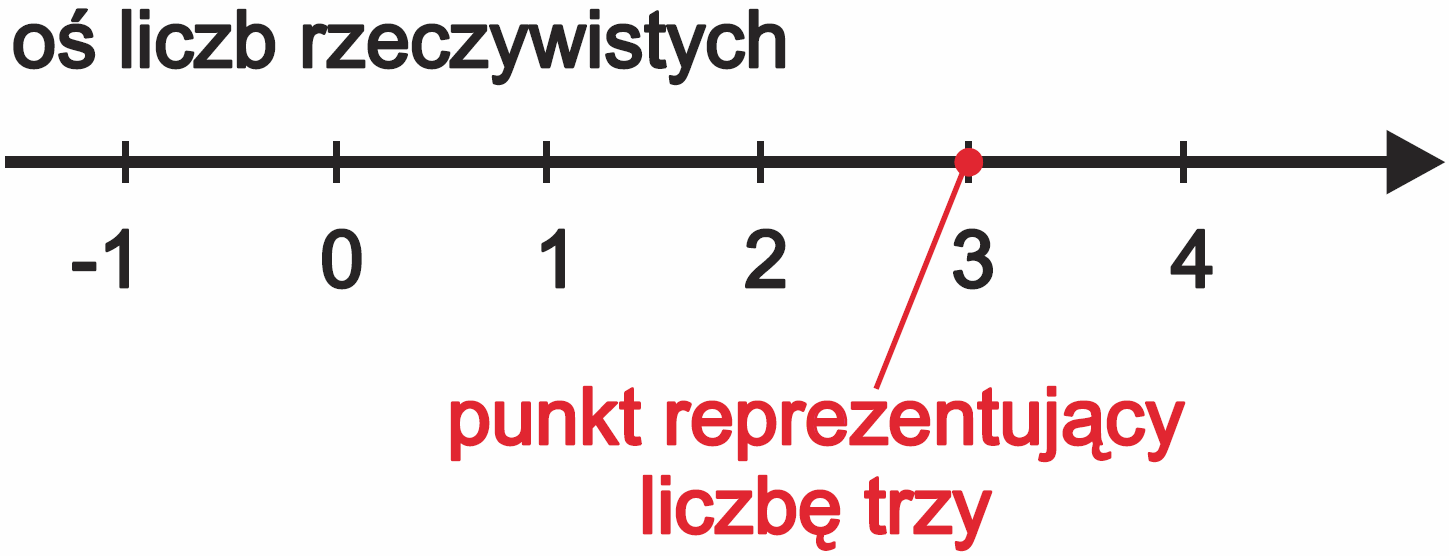
Zacznijmy więc od łatwego pytania: czy rezystancję R można wyrazić jedną liczbą? Oczywiście – wystarczy jedna „zwykła” liczba określająca wartość rezystancji w omach. Jak pamiętasz ze szkoły, graficzną reprezentacją liczb rzeczywistych jest oś liczbowa i na tej osi możemy zaznaczyć punkt – liczbę reprezentującą rezystancję R_A– rysunek 5.

A teraz kluczowe pytanie: czy reaktancję X_c też można wyrazić jedną liczbą? I jeszcze trudniejsze pytanie: czy impedancję Z można wyrazić jedną liczbą?

Zostawmy na razie impedancję, którą można potraktować jako coś złożonego. Pozostańmy przy reaktancji pojemnościowej X_c. Podobnie jak rezystancja R, tak też reaktancja X_c wydaje się być „elementarna”, „pojedyncza”. Czy nie czujesz przez skórę, że podobnie jak wartość rezystancji R zapisujemy jedną liczbą, tak i wartość reaktancji X_c też powinniśmy zapisać jedną liczbą? Ale jaka liczba zawiera też informację o kącie przesunięcia o 90 stopni?

Czy uważasz, że taka liczba NIE ISTNIEJE?

Nic dziwnego – właśnie tu jest najtrudniejszy punkt naszych rozważań.

Istnieje czy nie istnieje?

Jeśli znasz tylko liczby rzeczywiste, to istotnie nie możesz sobie wyobrazić, żeby reaktancję czy impedancję wyrazić jedną liczbą. Żaden z punktów osi liczbowej nie może reprezentować wartości reaktancji czy impedancji, bo nie ma tu żadnej informacji o kącie przesunięcia.

Czy to znaczy, że nie istnieje liczba, którą można byłoby precyzyjnie wyrazić reaktancję kondensatora, zarówno jej wartość, jak i przesunięcie? Ano właśnie…

Liczba to pojęcie abstrakcyjne. Co to właściwie znaczy, że liczba istnieje albo liczba nie istnieje? Czy na przykład liczba trzy istnieje?

Niewątpliwie istnieje. Ale kto widział liczbę 3 „w czystej postaci”?

Cyfra 3 wcale nie jest liczbą trzy „w czystej postaci”. To tylko jeden z wielu sposobów zapisu abstrakcyjnego pojęcia. Przecież liczbę 3 można zapisać jako cyfrę rzymską III albo w systemie dwójkowym jako 11₍₂₎. Liczbę trzy reprezentuje też hebrajska litera gimel ג, grecka gamma γ oraz arabski znak ٣. Liczbę trzy reprezentuje też punkt na rysunku 6.

Jednak ani 3, ani 11₍₂₎, ani III, ani punkt na rysunku 6 nie jest „liczbą trzy w czystej postaci”, ponieważ nie ma czegoś takiego jak „liczba w czystej postaci”. Nie mamy jednak wątpliwości, że liczba trzy istnieje, bo w naszym otoczeniu mamy mnóstwo przykładów, które są nierozerwalnie związane z liczbą trzy. Choćby to, że ja mam trzy lutownice, że trzeciego marca temperatura w południe wzrosła do trzech stopni Celsjusza powyżej zera, że mój kolega dopiero za trzecim podejściem zdał egzamin na prawo jazdy.

Liczba nie istnieje w sensie materialnym. Liczba to pojęcie abstrakcyjne, które wykorzystujemy do opisu różnych przejawów naszej rzeczywistości. Na przykład:
− w układzie pracują 4 tranzystory (liczba naturalna)
− średnia temperatura zimą wynosi –3,2°C (ujemna liczba ułamkowa)
− w obliczeniach wykorzystujemy liczbę π (liczba niewymierna).

Owszem, nie ma sensu stwierdzenie, że „w układzie pracuje –3,2 tranzystora”. Nie ma sensu, a raczej jest niemożliwe, żeby „temperatura spadła poniżej –400°”. W naszym świecie nie bardzo potrafimy też znaleźć praktyczne zastosowanie dla bardzo dużych i bardzo małych liczb. Na przykład szacowana liczba atomów we wszechświecie to około 10⁸⁰ (jedynka z osiemdziesięcioma zerami). Niemniej liczba 6184212973810650673891 25764610616446164541651646060616150 51654165467998976461661202258125441 0973160643247606542065420515475,217 istnieje, choć nie bardzo potrafimy znaleźć przykładu jej praktycznego zastosowania.

W starożytności nie znano pojęcia zera. Zauważ, że zera nie ma w rzymskim systemie liczenia – są tam tylko liczby naturalne. Nawet Babilończycy, setki lat wcześniej wykorzystujący sześćdziesiątkowy system, który można nazwać pozycyjnym, nie znali pojęcia zera i przy zapisywaniu liczb zamiast zera zostawiali puste miejsce. Czy jednak liczba zero w starożytności nie istniała? Czy w starożytności nie istniała niewymierna liczba Eulera e – podstawa logarytmów naturalnych?

Starożytni nie mieli potrzeb i możliwości wykorzystywania „dziwnych” liczb. Czy liczby te wtedy nie istniały?

Co to więc znaczy, że liczba istnieje? Być może powiesz, że liczba istnieje, jeżeli znajdujemy w naszym życiu jej praktyczne bądź potencjalne zastosowanie i jeśli potrafimy znaleźć jej graficzną reprezentację. A swoją drogą, to zdumiewająca sytuacja, że gdy pojawia się praktyczna potrzeba, znajduje się odpowiedni aparat matematyczny do jej opisu. Zauważ, że to właśnie rozwój nauki i techniki stwarzał „zapotrzebowanie” nie tylko na nowe liczby, ale i na sposoby przeprowadzania na tych liczbach operacji. Przecież najpierw do liczenia owiec, kóz, wołów i worków zboża wykorzystywano tylko liczby naturalne (bez zera), potem w związku z kolejnymi potrzebami zaczęto stosować ułamki, liczby ujemne, zero i wreszcie liczby niewymierne, takie jak π, e czy pierwiastek z trzech.

A teraz ujawniła się kolejna potrzeba: w naszej elektronicznej praktyce chcemy wykonywać obliczenia, i to nie tylko dotyczące rezystancji. Potrzebny jest jakiś ściśle matematyczny sposób zapisu oporności, który pozwoliłby zawrzeć też informacje o kącie i przeprowadzać niezbędne obliczenia, uwzględniające przesunięcie fazy. Wartość rezystancji potrafimy bez problemu wyrazić liczbą rzeczywistą. Natomiast mamy problem wyrażenia reaktancji pojemnościowej za pomocą jednej liczby.

W życiu codziennym wystarczają nam liczby rzeczywiste, których reprezentacją graficzną jest oś liczbowa. Ale wytłumacz mi, dlaczego graficzną reprezentacją liczby opisującej reaktancję X_c miałaby być jedynie oś liczb rzeczywistych? Dlaczego reprezentacją graficzną „pojemniejszych liczb” nie miałaby być płaszczyzna liczbowa?

Dlaczego nie? Czy tylko dlatego, że do tej pory nie potrzebowaliśmy takich „dziwnych liczb”?

Fakt, że dla takich liczb do tej pory nie znajdowaliśmy zastosowania w życiu codziennym, nie znaczy, że one nie istnieją. Nieznajomość pojęcia logarytmów naturalnych w starożytności nie znaczy, że liczba e wtedy nie istniała!

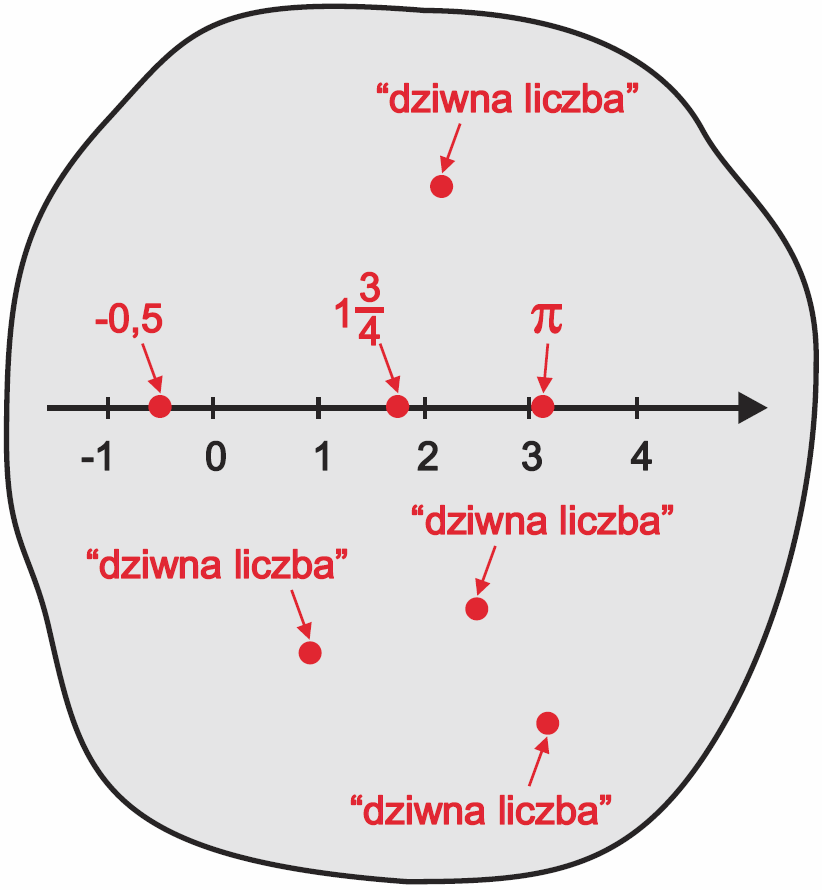
Przyjmij więc do wiadomości, że istnieją „dziwne liczby”, których reprezentacją graficzną są punkty płaszczyzny. Dobrze nam znane liczby rzeczywiste są tylko drobną częścią zbioru tych „dziwnych liczb”. Na rysunku 7 masz przykład zaznaczenia na takiej płaszczyźnie kilku „zwykłych” liczb rzeczywistych oraz kilku „dziwnych liczb”, nieleżących na osi liczb rzeczywistych.

Idźmy krok dalej: a dlaczego graficzną reprezentacją liczb nie miałaby być cała przestrzeń, a nie tylko jedna płaszczyzna?

Tak! To wcale nie jest głupia myśl.

Jak najbardziej istnieją „jeszcze dziwniejsze liczby”, których graficzną reprezentacją jest nie tylko oś liczbowa, nie tylko płaszczyzna, ale cała przestrzeń liczbowa. Mało tego – można sobie wyobrazić „jeszcze bardziej skomplikowane liczby”, których reprezentacją graficzną byłyby przestrzenie cztero-, piecio-, czy więcej wymiarowe. Takowe liczby też istnieją, ale ich nie wykorzystujemy, ponieważ nie mamy aż takich potrzeb. Na razie mamy stosunkowo prostą potrzebę opisania jedną liczbą reaktancji X_c i impedancji Z. Okazuje się, że do tego znakomicie nadają się „dziwne liczby”, których graficzną reprezentacją są punkty leżące na płaszczyźnie liczbowej.

A oto inny ważny aspekt stwierdzenia, że „liczba istnieje”. Można powiedzieć obrazowo, że dane liczby istnieją, jeśli zbiór tych liczb wraz z działaniami na nich tworzy harmonijną całość, bez sprzeczności. Niewątpliwie tak jest w przypadku liczb rzeczywistych i wszelkich działań na nich: nie tylko dodawania i odejmowania, ale też mnożenia, dzielenia, potęgowania, pierwiastkowania, logarytmowania…

Otóż okazuje się, że już wiele lat temu matematycy, „marnujący czas” na teoretyczne rozważania, doszli do wniosku, że wszystkie znane działania matematyczne można rozszerzyć także na „dziwne liczby”, reprezentowane przez wszystkie punkty płaszczyzny liczbowej. Można powiedzieć, że stworzyli wtedy interesującą, spójną teorię, i… odłożyli ją na półkę.

Okazuje się więc, że od kilkuset lat istnieje cały spójny system, obejmujący nie tylko „dziwne liczby”, ale też wszystkie działania na nich, podobnie jak na „zwykłych” liczbach rzeczywistych. Tylko przed kilkuset laty była to jedynie ciekawostka matematyczna. W tamtych czasach nie tylko o elektronice nikt jeszcze nie marzył i matematycy też nie widzieli dla „dziwnych liczb” żadnego praktycznego zastosowania. Nie widząc w znanym im świecie jakiegokolwiek zastosowania dla „dziwnych liczb”, zupełnie niefortunnie nazwali je liczbami urojonymi (imaginary numbers), w przeciwieństwie do liczb rzeczywistych (real numbers).

Dopiero w XIX wieku okazało się, że te „liczby urojone” wcale nie są urojone. Są to najprawdziwsze liczby, bardzo potrzebne w praktyce. Jednak nieszczęśliwa nazwa „liczby urojone” pokutuje do dziś i straszy początkujących. Jeszcze bardziej straszy nieszczęsny pierwiastek z minus jeden…

Zupełnie niepotrzebnie!

W następnym odcinku zajmiemy się problemem wyrażenia reaktancji i impedancji za pomocą „dziwnych liczb”, które nazywają się liczbami zespolonymi.

Piotr Górecki