Elektronika (nie tylko) dla informatyków (23) Równoległy obwód rezonansowy – zależności

W poprzednim odcinku zaczęliśmy analizować równoległy obwód rezonansowy. W tej części przyjrzymy się bliżej tego typu obwodom i poznamy ich niektóre ważne właściwości.

Szerokość pasma

Zarówno szeregowe obwody rezonansowe, jak i równoległe, są wykorzystywane w roli filtrów. A wtedy interesuje nas, jak te filtry zachowują się nie tylko dokładnie przy częstotliwości rezonansowej, ale też w pobliżu częstotliwości rezonansowej.

W tym celu należałoby zbadać przebieg tak zwanych krzywych rezonansowych, dotyczących prądu, napięcia i oporności. Nie ulega wątpliwości, że dla częstotliwości rezonansowej filtr ma maksymalną „skuteczność”. A czym dalej od częstotliwości rezonansowej, tym działanie filtru jest słabsze. Problem w tym, że charakterystyka filtru jest gładka, nie ma na niej jakiegoś załamania i punktów charakterystycznych, a trzeba przyjąć jakieś punkty graniczne. W ten sposób oprócz częstotliwości środkowej f₀, wyznaczone zostaną częstotliwości graniczne filtru: dolna f_d i górna f_g oraz pasmo przenoszenia o szerokości f_g-f_d, oznaczane Δf albo B lub Bw od angielskiego bandwidth.

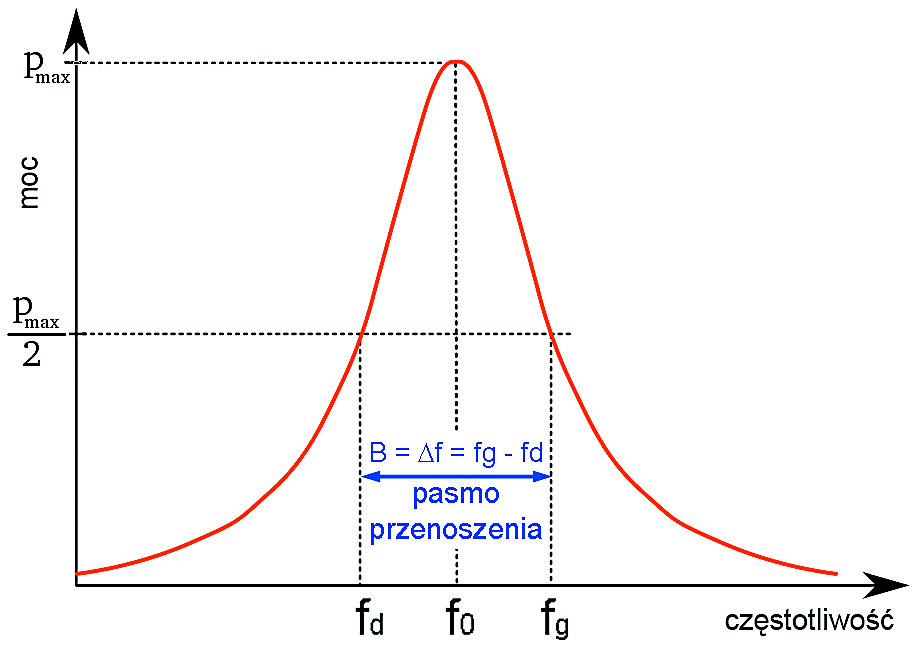
Już od dawna jako punkty graniczne przyjęto częstotliwości, przy których moc sygnału spada o połowę, czyli dwukrotnie, w stosunku do mocy przy częstotliwości f₀. Jak wiadomo, dla mocy spadek o połowę, czyli dwukrotny to zmiana o –3 decybele. Dlatego najczęściej mówimy o paśmie trzydecybelowym, a znacznie rzadziej pasmo 3-decybelowe nazywa się też pasmem połowy mocy. Ilustruje to rysunek 1.

Ale w praktyce, w przypadku filtrów zdecydowanie częściej mówimy o napięciach, a nie o mocy. I tu trzeba pamiętać, że dla napięć i prądów 3 decybele to zmiana (pomnożenie lub podzielenie) przez pierwiastek z dwóch (√2≅1,41). Pomnożenie lub podzielenie napięć i prądów przez pierwiastek z dwóch nadal oznacza dwukrotną zmianę mocy. Nadal jest to więc to samo pasmo połowy mocy. Charakteryzując „skuteczność” filtru, zawsze podajemy te same częstotliwości graniczne f_g, f_d, przy których charakterystyka obniża się o 3 dB, czyli dla mocy do wartości 50%, a dla napięć do wartości U_max/1,41, co częściej podajemy w postaci 0,707×U_max. Po prostu zamiast dzielić przez pierwiastek z dwóch, mnożymy przez jego odwrotność. W zasadzie 1/√2= 0,707106781…, jednak w praktyce tak wysoka dokładność nie jest potrzebna, więc mnożymy przez 0,707 lub 0,71 albo w mniej dokładnych zastosowaniach nawet przez 0,7.

Okazuje się, że jeśli właśnie tak zdefiniujemy częstotliwości graniczne f_g, f_d, to zależności matematyczne będą zaskakująco proste. Już intuicja podpowiada, że czym większa dobroć obwodu, tym bardziej ten obwód „lubi swoją częstotliwość rezonansową”, a „mniej lubi obce częstotliwości”. I rzeczywiście, o wszystkim decyduje dobroć obwodu rezonansowego, która, jak pamiętamy, jest stosunkiem oporności: Q = ρ/Rs = Rr/ρ I właśnie dobroć Q decyduje też o szerokości pasma: czym większa dobroć, tym węższe jest pasmo przenoszenia według dziecinnie prostej zależności:

Δf = f₀/Q którą można też zapisać: f₀/Δf = Q

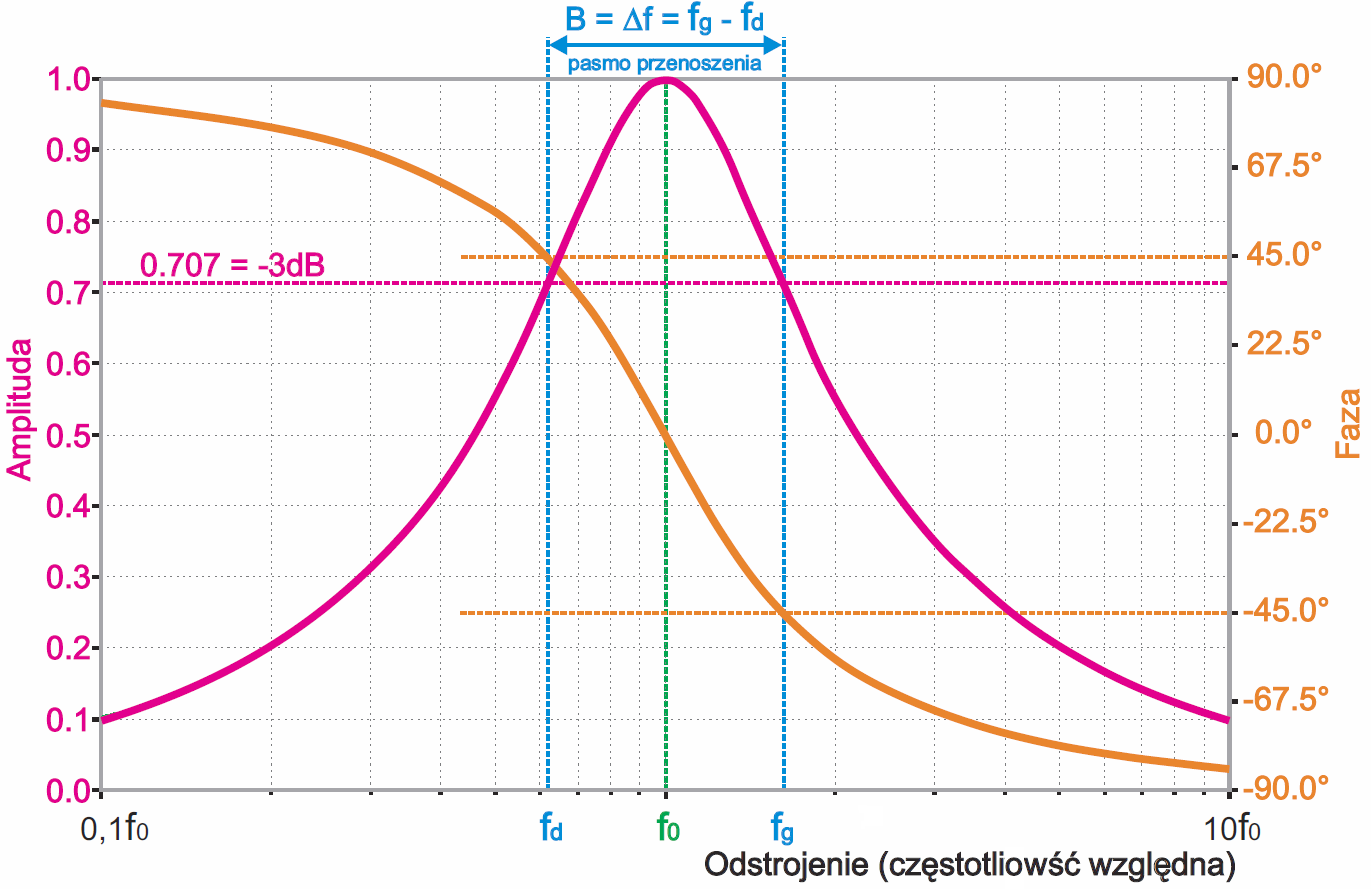
Na rysunku 2 pokazane są tak zwane uniwersalne krzywe rezonansowe – można je stosować do prądu, napięcia, jak i oporności, i to zarówno obwodu równoległego, jak i szeregowego, a co ważne, o dowolnej dobroci. Co ciekawe, przy częstotliwościach granicznych pasma połowy mocy f_d i f_g przesunięcie fazowe między napięciem i prądem w obwodzie RLC wynosi dokładnie –45 stopni i 45 stopni, czyli w mierze kątowej –π/4 i π/4 radiana. Obrazuje to pomarańczowa krzywa i skala z prawej strony rysunku 2.

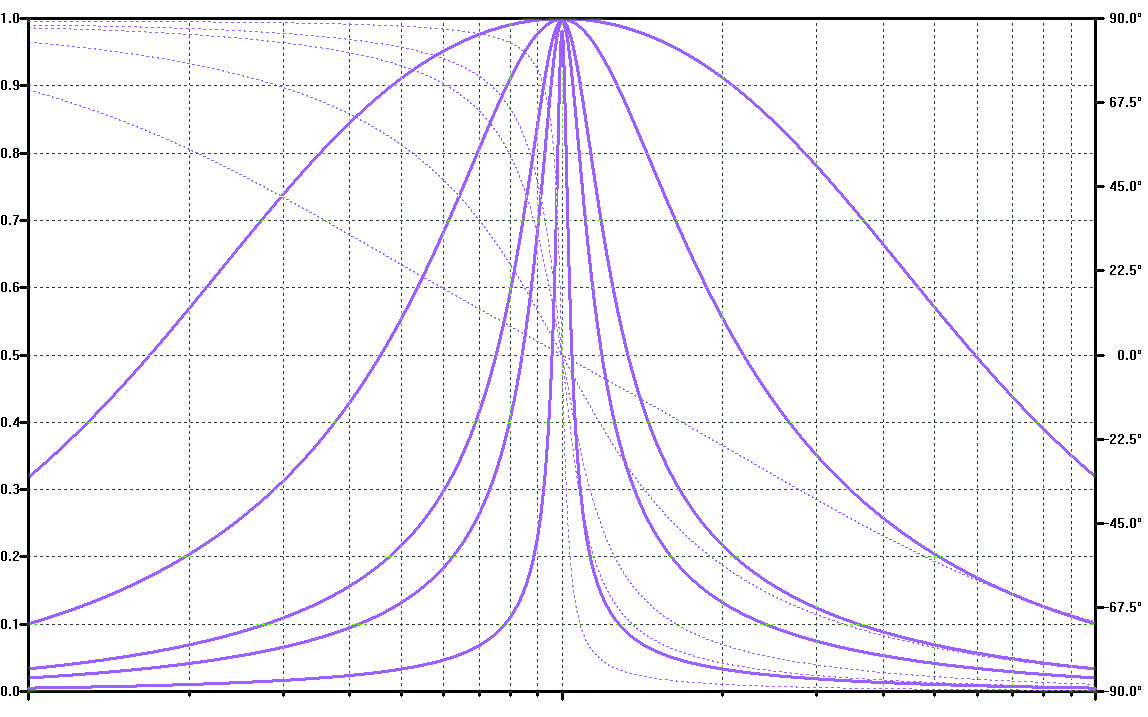
Tylko w idealnym obwodzie rezonansowym przesunięcie fazy nie zmieniało się płynnie, tylko przy częstotliwości rezonansowej niejako „przeskakiwało” z jednej skrajnej wartości do drugiej (90° i –90°) – porównaj rysunek 6 w poprzednim odcinku. W obwodach ze stratami, czyli w obwodach RLC nie ma gwałtownego „przeskoku fazy”. Dla częstotliwości rezonansowej przesuniecie fazy wynosi dokładnie 0 stopni – dlatego też przyjęliśmy, że dla idealnego obwodu przy f₀ przesunięcie wynosi zero, choć w zasadzie trudno tam było mówić o przesunięciu, jeśli prąd był równy zeru. W obwodzie ze stratami charakterystyczne jest właśnie to, że dla częstotliwości granicznych pasma połowy mocy przesunięcie fazy zawsze wynosi 45 stopni. Ale może wcześniej widziałeś w podręcznikach charakterystyki obwodów o różnej dobroci pokazane mniej więcej tak, jak na rysunku 3?

Otóż nie ma tu żadnej sprzeczności. Zwróć uwagę, że na rysunku 2 na osi poziomej nie mamy podanej wprost częstotliwości, tylko odstrojenie od częstotliwości f₀. Odstrojenie możemy łatwo przeliczyć na „prawdziwą” częstotliwość, uwzględniając właśnie dobroć Q i wartość f₀. Dlatego też jedna krzywa z rysunku 2 dotyczy dowolnej dobroci Q, a krzywe o różnej dobroci byłyby rozciągnięte lub ściśnięte wzdłuż poziomej skali „prawdziwej” częstotliwości, jak na rysunku 3. Ale w te szczegóły nie będziemy się wgłębiać.

Na razie chciałbym zwrócić uwagę, że podstawowe wnioski i wzory są zaskakująco proste: pasmo B = f₀/Q i przesunięcie fazy dla częstotliwości granicznych wynosi 45 stopni. Powinieneś je zapamiętać. Dziś wprawdzie obwody rezonansowe nie są już tak często wykorzystywane jak kiedyś, dlatego nie jest konieczne wgłębianie się we wszystkie szczegóły. Jednak warto nawet dla ciekawości mieć nieco szerszy obraz zagadnienia, ponieważ te same lub podobne zależności potrzebne są nie tylko przy analizie obwodów rezonansowych LC.

Jak i dlaczego?

Zależność szerokości pasma B od dobroci jest wprawdzie dziecinnie prosta (B = f₀/Q), jednak warto wyjaśnić kilka szczegółów.

Oto jeden z nich: w praktyce trzeba pamiętać, że szerokość pasma B(Δf) wyznaczona jest przez częstotliwości f_d, f_g, które jak wskazywałyby rysunki 1 i 2, leżą „w jednakowej odległości” od częstotliwości środkowej f₀. Inaczej mówiąc, częstotliwość rezonansowa f₀ leży w „połowie drogi” pomiędzy f_d i f_g. I tak rzeczywiście jest, ale…

… w naszym życiu codziennym przyzwyczajeni jesteśmy do miary liniowej. Dlatego dla przypadku, gdy częstotliwość środkowa wynosi 1 kHz i pasmo B też jest równe 1 kHz (Q=1), prawdopodobnie pomyślimy, że f_d=0,5 kHz i f_g=1,5 kHz, ponieważ 1 kHz to średnia arytmetyczna częstotliwości 1,5 kHz i 0,5 kHz. Istotnie, różnica f_g-f_d wynosi 1 kHz, ale zakres 0,5…1,5 kHz nie jest pasmem tego obwodu! Otóż w przyrodzie i technice „naturalną” miarą zazwyczaj okazuje się miara logarytmiczna. Zamiast średniej arytmetycznej należy wziąć średnią geometryczną. Gdybyśmy zadali sobie trochę trudu i rozwiązali równanie kwadratowe, okaże się, iż w grę wchodzą liczby:

(√5 – 1)/2 ≅ 0,61803398874989484820…

oraz

(√5 + 1)/2 ≅ 1,61803398874989484820…

I znów wszystko pasuje, ponieważ różnica częstotliwości 1,618… kHz i 0,618… kHz też wynosi dokładnie 1 kHz.

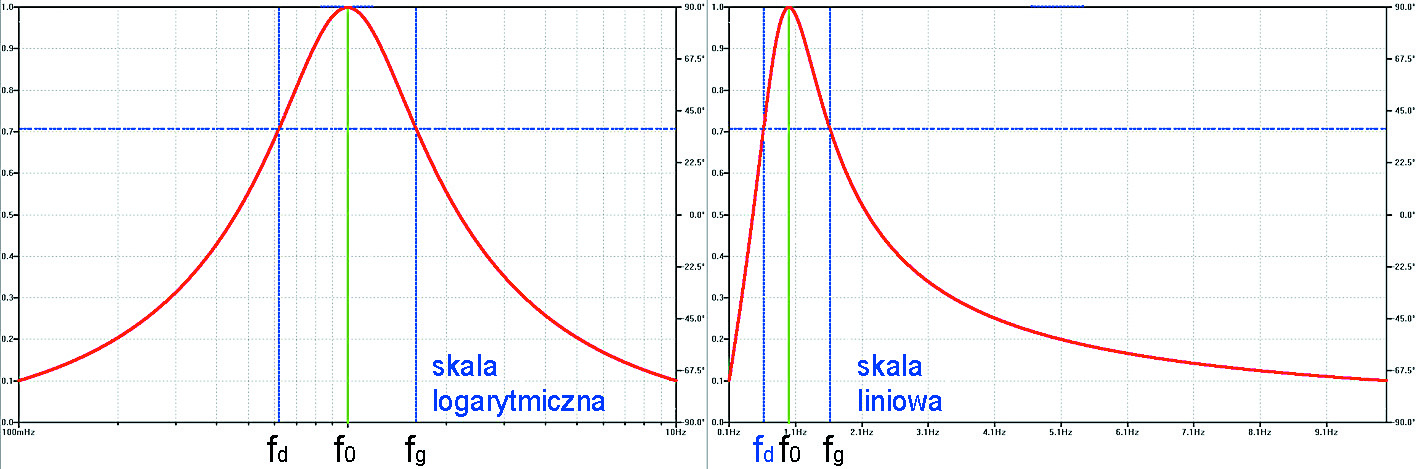
Przy tej okazji jeszcze raz zwrócę Twoją uwagę na zalety miary logarytmicznej. I tak na przykład elegancki i symetryczny wykres z rysunku 1 z zaznaczonym pasmem połowy mocy (3 dB) wyglądałby dziwnie w skali liniowej – porównanie masz na rysunku 4. Nie dziw się więc, że w elektronice bardzo często korzystamy z miary logarytmicznej, która naprawdę okazuje się bardziej naturalna od miary liniowej.

A teraz inny szczegół, znacznie trudniejszy. Większość elektroników nie czuje intuicyjnie zależności między dobrocią, szerokością pasma i związaną z tym stromością charakterystyki. Spróbujmy przybliżyć te zagadnienia.

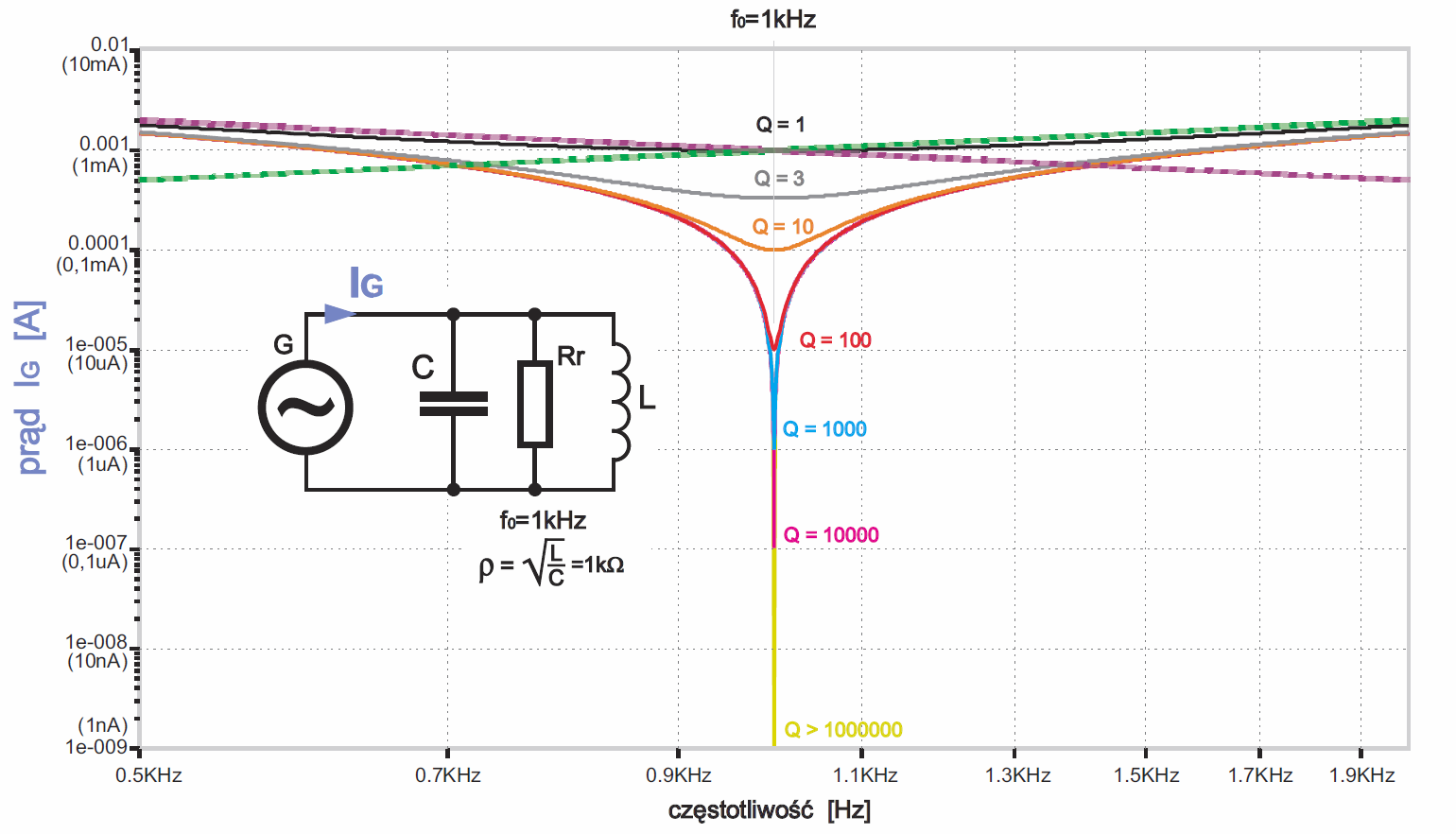
Zapoznajmy się bliżej z przebiegiem prądu źródła przy obwodach o różnej dobroci. Pokazuje to rysunek 5, gdzie różnymi kolorami zaznaczony jest przebieg prądu dla obwodów o różnej dobroci, czyli różnej rezystancji strat R_r. Nasz wykres dotyczy zachowania obwodu RLC w wąskim zakresie częstotliwości (500 Hz…2 kHz). Parametry obwodu są tak dobrane (L = 0,159…H, C = 0,159…uF), żeby częstotliwość rezonansowa f0 wynosiła 1 kHz, a rezystancja charakterystyczna ρ też miała „okrągłą” wartość 1 kΩ. Napięcie generatora U_G wynosi 1 V.

Najpierw zwróć uwagę na proste, przerywane linie: fioletową i zieloną, które pokazują, jaki jest prąd w cewce i kondensatorze. Prąd płynący przez kondensator rośnie ze wzrostem częstotliwości, prąd cewki – maleje. Analizowaliśmy to już na rysunku 2 w poprzednim odcinku, (porównaj też rysunek 6, gdzie przedstawiona była oporność X_C i X_L również w poprzednim odcinku). Przy częstotliwości rezonansowej f₀ prądy te są równe, a ich wartość wynosi:

I₀ = U_G/X_C = U_G/X_L = U_G/ρ

W naszym przypadku U_G = 1 V, ρ = 1 kΩ, więc I₀ = 1 mA. W obwodzie o doskonałej dobroci prąd źródła sygnału I_G przy częstotliwości rezonansowej f₀ zmalałby do zera, jak pokazuje żółta linia na rysunku 5. Natomiast w przypadku obwodów o ograniczonej dobroci, prąd przy częstotliwości f₀ zmniejszy się do wartości minimalnej, równej:

I_Gmin = U_G/R_r pamiętając, że R_r = Q×ρ, napiszemy: I_Gmin = UG/Q×ρ pamiętamy, że I₀= U_G/ρ, więc: I_Gmin = I₀/Q

Dla naszego przykładowego obwodu U_G = 1 V, ρ = 1 kΩ, czyli I₀= 1 mA, więc: I_Gmin = 1 mA/Q

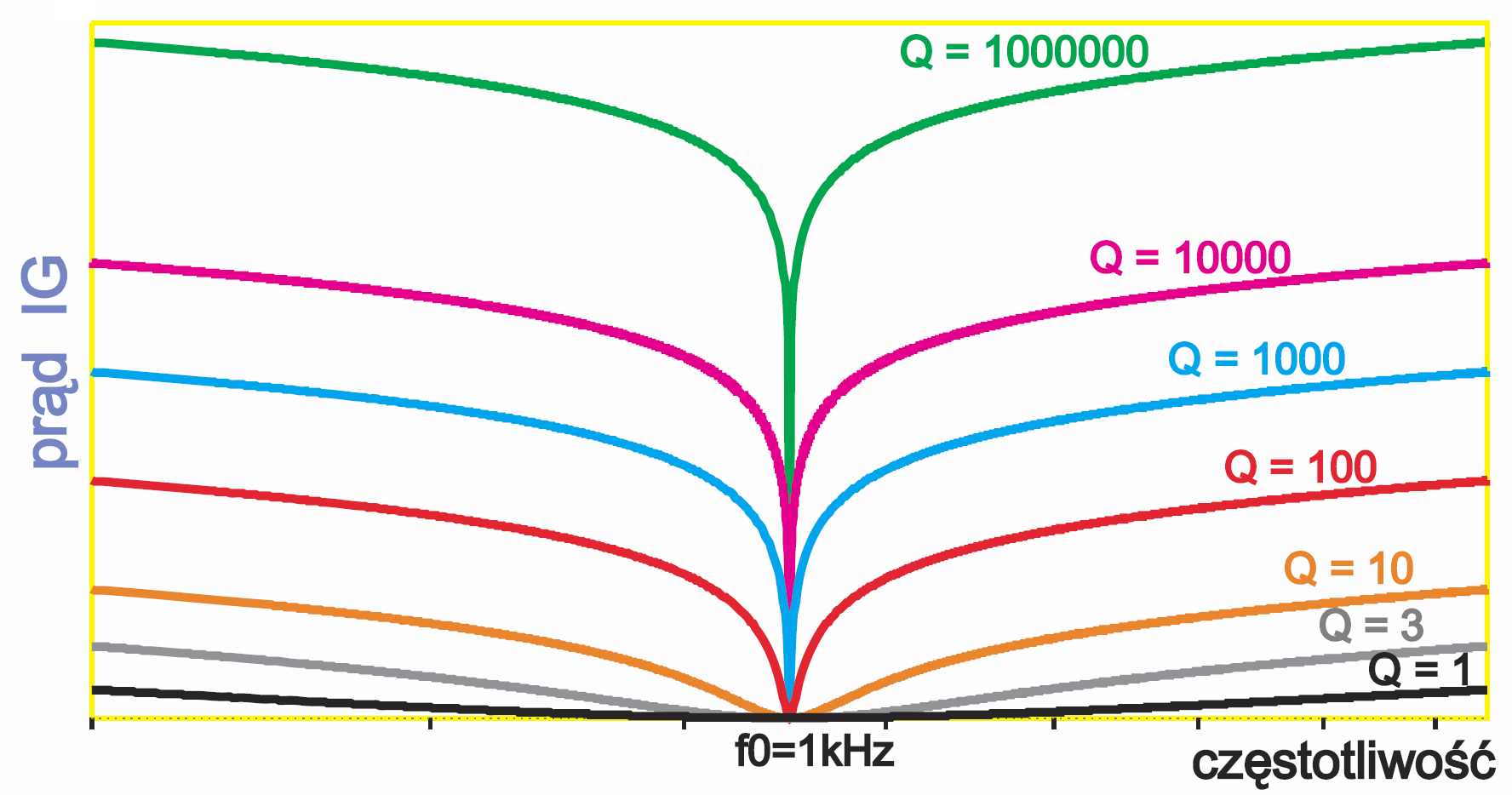
Kolorowe krzywe na rysunku 5 pokazują wyraźnie, że w każdym przypadku prąd minimalny generatora przy częstotliwości rezonansowej f₀ jest równy U_G/R_r. Ale nadal nie widać tu wyraźnie zależności szerokości pasma od dobroci. Aby pokazać tę zależność, należałoby potraktować prąd minimalny jako punkt wyjścia, dla każdej krzywej zaznaczyć prąd pierwiastek z dwóch razy większy (w przybliżeniu 1,41 × I_min) i sprawdzić pasmo przy takim prądzie. Należałoby tak poprzesuwać krzywe, żeby ich wierzchołki znalazły się w jednym punkcie, mniej więcej jak na rysunku 6.

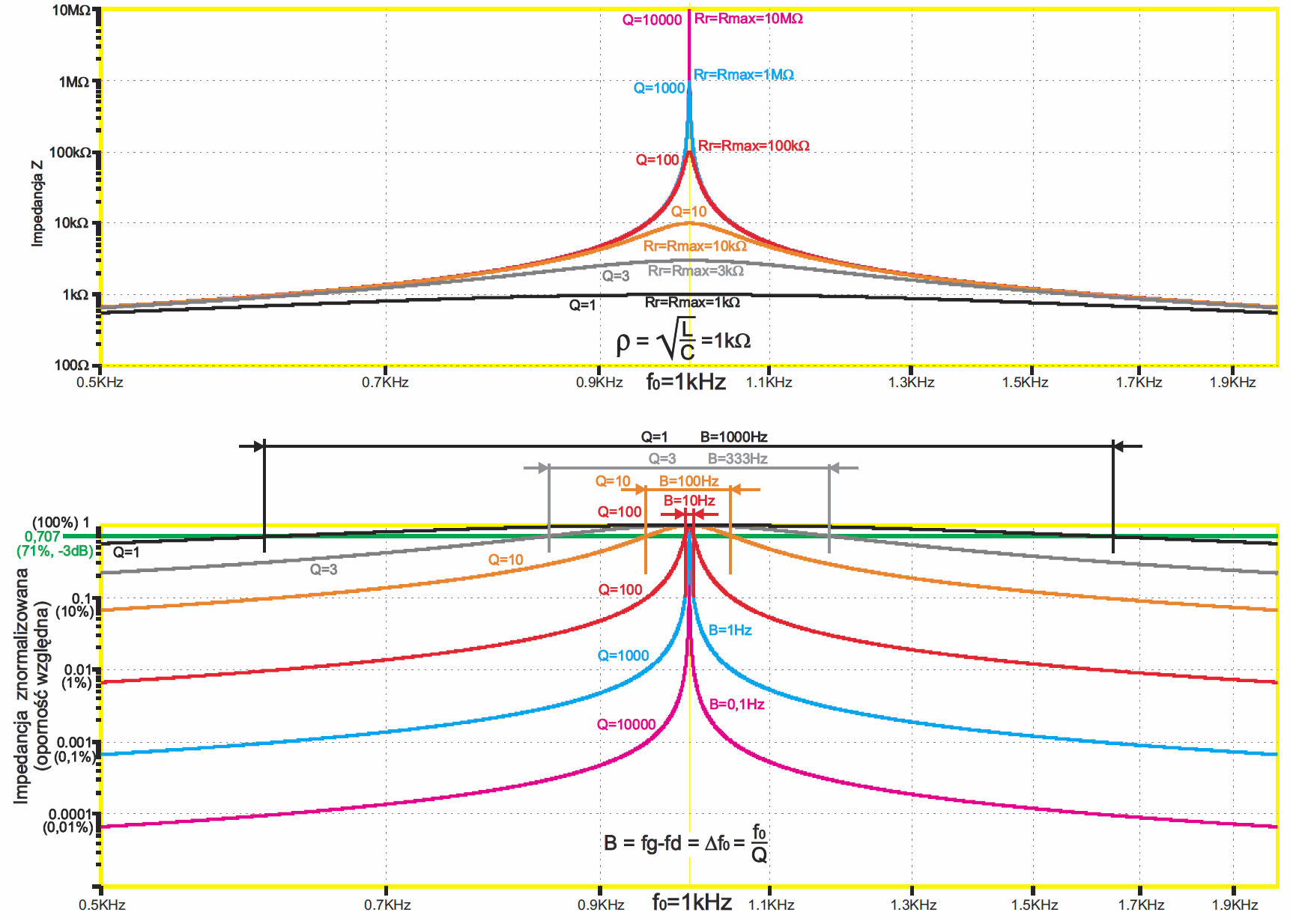
My przeanalizujemy to dokładniej, ale na rysunku pokazującym nie prąd, tylko oporność obwodów o różnej dobroci z rysunku 5. Wcześniej mieliśmy już rysunek 6 w poprzednim odcinku, który pokazuje przypadek idealny, przy nieskończenie wielkiej dobroci. I tak w górnej części rysunku 7 masz stosowne wykresy wypadkowej oporności obwodów o różnej rezystancji strat R_r i tym samym o różnej dobroci Q – to jakoby „odwrócony” odpowiednik rysunku 5. Jak widać, dla częstotliwości odległych od f₀, przebieg krzywych jest praktycznie taki sam, niezależny od R_r i dobroci. Różnice dotyczą tylko częstotliwości bliskich f₀ i niewątpliwie są związane z dobrocią.

I znów dla uchwycenia interesującej nas zależności trzeba tak przesunąć krzywe, żeby ich wierzchołki znalazły się w jednym punkcie. Masz to w dolnej części rysunku 7. Są to te same krzywe, co w górnej części rysunku, tylko przeskalowane tak, że oporność względna przy częstotliwości rezonansowej jest równa 100%, czyli 1. Można powiedzieć, że są to wykresy impedancji znormalizowanej obwodów RLC o różnej dobroci. Pozioma zielona linia pokazuje wartość oporności względnej o wartości 0,707×R_max (0,707R_r), czyli pierwiastek z dwóch razy mniejszej od maksymalnej, czyli mniejszej o 3 dB od R_r. Przecięcie tej poziomej zielonej linii z daną krzywą pokazuje szerokość pasma obwodu o danej dobroci. I dopiero tutaj jasno widać związek dobroci z szerokością pasma przepustowego.

Przeanalizuj starannie materiał z ostatnich odcinków, bo warto rozumieć właściwości obwodów rezonansowych. Ponieważ jednak współczesny elektronik nieczęsto ma do czynienia z obwodami rezonansowymi LC, dlatego nie będę tłumaczył dalszych zagadnień, a byłoby jeszcze sporo do tłumaczenia.

Wspomnę tylko o kilku ważnych szczegółach. I tak na przykład ostatnie rysunki zasadniczo dotyczą równoległego obwodu rezonansowego. Jednak okazuje się, że zależności te są słuszne także dla rezonansowego obwodu szeregowego. Świadczy o tym choćby podobieństwo wzorów na impedancję obwodów dla równoległego:

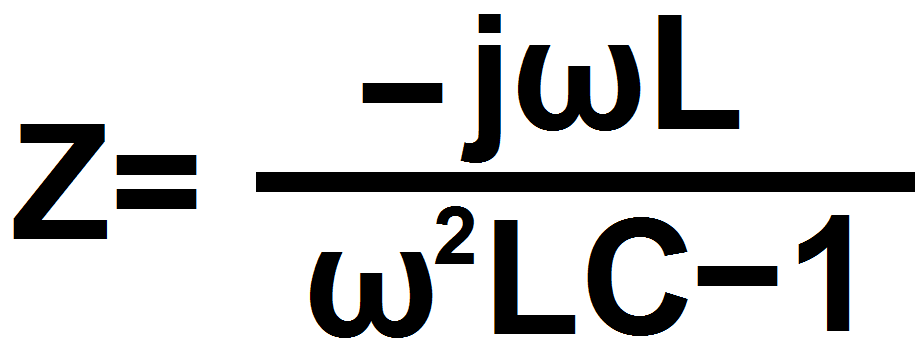
i szeregowego:

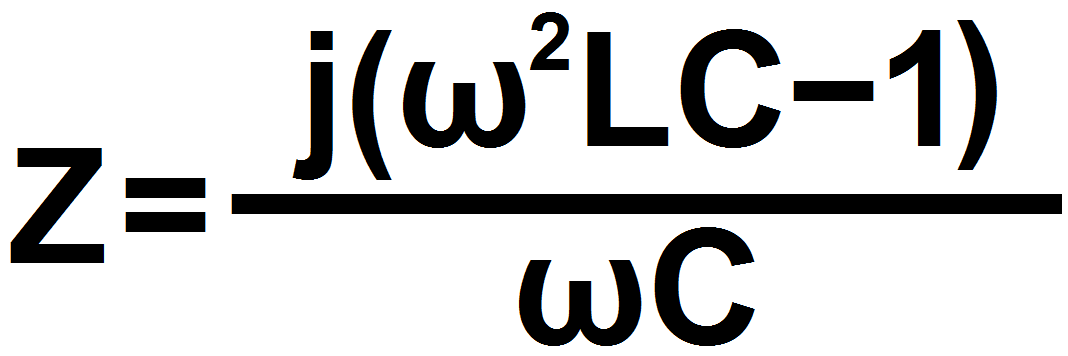
Dlatego też często spotyka się tzw. uniwersalne krzywe rezonansowe – patrz wcześniejszy rysunek 2.

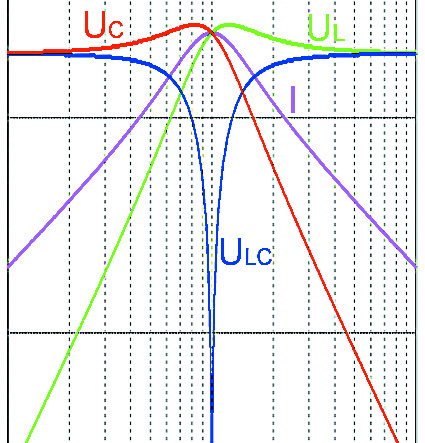
Warto też pamiętać, że zarówno w podręcznikach szkoły średniej, jak i w skryptach akademickich spotyka się odmienne wzory, niepodobne rysunki i porównanie takich materiałów wygląda na jakiś bałagan, a nawet na sprzeczność. Nie jest to jednak sprzeczność, tylko efekt różnego podejścia do obszernego i dość trudnego zagadnienia oraz efekt różnych sposobów obrazowania wyników (np. w skali liniowej i logarytmicznej). My w naszych uproszczonych rozważaniach praktycznie nie poruszyliśmy tematu rozstrojenia względnego i bezwzględnego. Nie mówiliśmy też nic o tym, że na przykład w szeregowym obwodzie rezonansowym maksimum napięcia na cewce i kondensatorze nie występuje przy częstotliwości rezonansowej, tylko tuż obok, jak pokazuje rysunek 8. Jeśli chcesz, przeanalizuj to sam. Weź wtedy pod uwagę, że mamy tu dwa czynniki, które się nakładają: zmiana reaktancji w funkcji częstotliwości i zmiana prądu. Inaczej jest z napięciem na (niezmiennej) rezystancji, które jest wprost proporcjonalne do prądu, a inaczej z napięciem na reaktancjach, które zmieniają swoją wartość w funkcji częstotliwości.

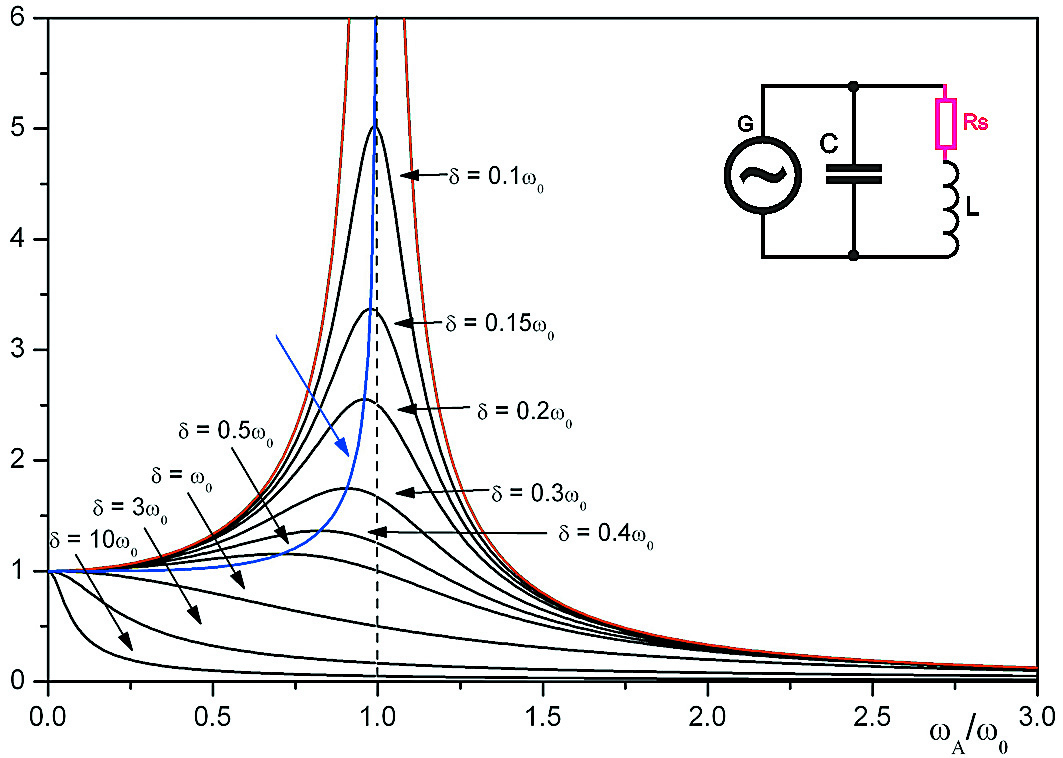
Innym przykładem są wykresy krzywych rezonansowych podobne jak na rysunku 9, gdzie niepokojący jest przebieg charakterystyki w lewej części rysunku. Nie ulega wątpliwości, że przy bardzo małych częstotliwościach wszystkie krzywe przebiegają tu płasko. U nas na rysunku 2 było inaczej. Dlaczego?

Wynika to z przyjętego do analizy modelu z rezystancją R_s, włączoną w szereg z cewką, co pokazane jest w prawym górnym rogu rysunku 9. To właśnie rezystancja R_s powoduje taki przebieg charakterystyki przy małych częstotliwościach. Ale nadal, po porównaniu rysunków 9 i 2, może się pojawić rozpaczliwe pytanie: to jaka jest prawda? Jeszcze raz podkreślam, że analizujemy uproszczone modele, a rzeczywistość jest znacznie bardziej skomplikowana, ponieważ w grę wchodzi szereg jeszcze innych czynników.

Trzeba też podkreślić, że niektóre akademickie rozważania i matematyczne analizy obwodów rezonansowych nie mają wartości praktycznej. Między innymi dlatego, że część rozważań dotyczy obwodów RLC o bardzo małej dobroci, czyli o bardzo dużym tłumieniu. Matematyczna analiza pewnych takich przypadków wskazuje, że… rezonans zachodzi tam przy każdej częstotliwości. Teoretycznie wszystko się zgadza, ale nijak ma się to do praktycznych obwodów rezonansowych, których dobroć Q wynosi zwykle od kilku do kilkuset. Praktyk powie, że przy dobroci rzędu 1 i mniejszej nie powinniśmy mówić o obwodzie rezonansowym i filtrze, a takie przypadki można i trzeba rozważać, ale na zajęciach automatyki i teorii sterowania.

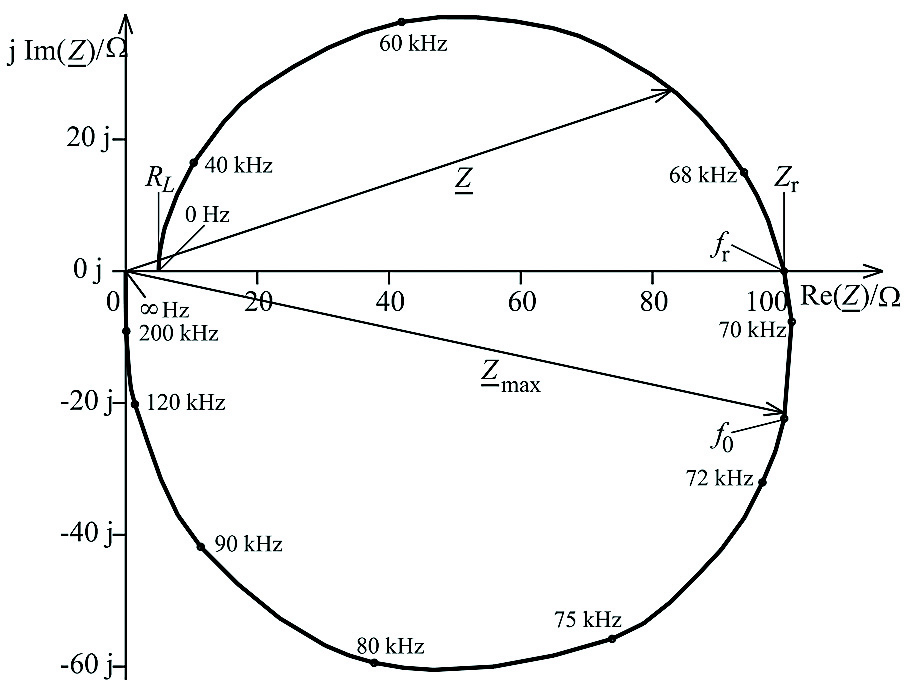
A oto jeszcze inny przykład: pochodzący z Wikipedii rysunek 10 w niecodzienny sposób pokazuje przebieg impedancji równoległego obwodu rezonansowego o parametrach C = 0,1 uF, L = 50 uH, R_s = 5 Ω.

Wcześniej na rysunku 10 w tym odcinku mieliśmy analogiczny wykres dla obwodu szeregowego. Nie byłoby w tym nic dziwnego, jest to bowiem przedstawienie impedancji na płaszczyźnie zespolonej, dzięki czemu można odczytać zarówno moduł (długość wektora) jak i argument (kąt przesunięcia fazowego). Jednak niepokoi fakt, że wyliczona ze wzoru

częstotliwość rezonansowa wynosi 71,176 kHz, natomiast z rysunku 10 wynika, że zerowe przesuniecie fazowe, czyli rezonans, następuje przy częstotliwości znacząco niższej! Okazuje się, że obecność rezystancji strat nie tylko zmniejsza dobroć, ale też zmniejsza częstotliwość rezonansową, która w omawianym przypadku (C = 0,1 uF, L = 50 uH, R_s = 5 Ω) wynosi 69,374 kHz. W praktyce taką różnicę pomijamy, ponieważ zmiana częstotliwości jest niewielka, mniejsza niż tolerancja użytych elementów. Jednak do tego wątku jeszcze wrócimy, bo otworzy on mam drogę do czegoś tak ważnego, ale i egzotycznego, jak częstotliwość zespolona i płaszczyzna s.

A w kolejnym odcinku przyjrzymy się równoległym obwodom rezonansowym od strony praktycznej.

Piotr Górecki