NanoVNA – precyzyjne pomiary część 1
Przyrząd NanoVNA pomimo niskiej ceny ma bardzo duże możliwości pomiarowe oraz pozwala osiągnąć zaskakująco dużą dokładność pomiarów w szerokim zakresie częstotliwości. Jednak uzyskana precyzja i dokładność zależą od wykorzystanych metod pomiarowych oraz sposobu i jakości kalibracji.
Wcześniej, w dwuczęściowym artykule (MR091 i MR092) zapoznaliśmy się z wyjątkowo pożytecznym przyrządem zwanym NanoVNA. Jak na razie, wykorzystaliśmy drobny ułamek jego możliwości, bowiem mierzyliśmy tylko impedancję elementów z wykorzystaniem tylko jednego portu i parametru S11. Sposób jest prosty, bowiem badany element jest dołączany wprost do portu Ch0.
Problem w tym, że przy takim sposobie pomiaru w sensowny sposób można mierzyć impedancje o wartościach niezbyt różniących się od 50 omów. W pierwszym przybliżeniu można przyjąć, że zakres pomiarowy dający sensowne wyniki rozciąga się wtedy mniej więcej od 0,5Ω do 5000Ω. Tymczasem w wielu przypadkach chcielibyśmy mierzyć impedancje dużo mniejsze, na przykład wartość rezystancji ESR kondensatorów, która może być rzędu kilkudziesięciu miliomów lub jeszcze mniej. Ale chcemy też mierzyć impedancje dużo większe, na przykład przebieg impedancji cewki (dławika) w funkcji częstotliwości, a wtedy impedancja przy rezonansie własnym może sięgnąć wielu kiloomów. Chcemy też mierzyć, jak przy zmianach częstotliwości zmieniają się właściwości rezystorów o wartościach z bardzo szerokiego zakresu.
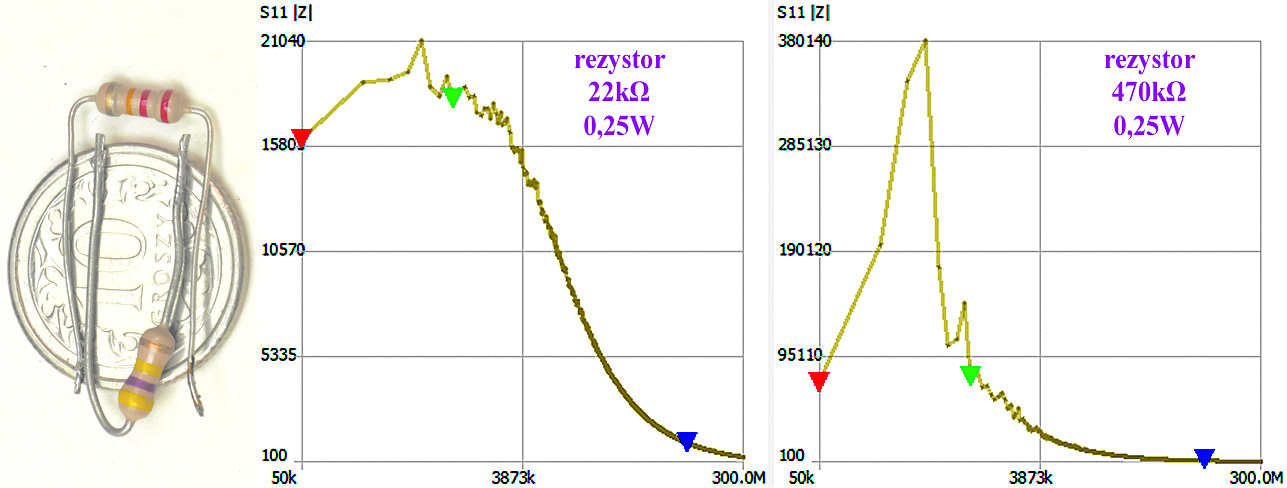
Prosty sposób pomiaru z wykorzystaniem jedynie gniazdka Ch0 i parametru S11 nie da wtedy wiarygodnych wyników. Trzeba poszukać innych rozwiązań. Oto one. Otóż można wykorzystać dwa inne, bardzo proste do zrealizowania sposoby. Przykładem może być próba pomiaru zwyczajnych ćwierćwatowych rezystorów THT 22kΩ oraz 470kΩ przez dołączenie wprost do gniazda Ch0. Wyniki pokazane są na rysunku 1.
Widać wprawdzie, że wskutek pojemności własnej rezystora jego impedancja ze wzrostem częstotliwości maleje, ale wyniki są mało użyteczne i praktycznie nieakceptowalne już dla rezystora 22kΩ. Tym bardziej dla rezystora 470kΩ. Dla porównania, na rysunku 2 pokazane są wyniki pomiarów tych samych dwóch rezystorów, ale przeprowadzonych w inny sposób.
Co prawda skala i wykres są odwrócone, niemniej tutaj zdecydowanie lepiej można określić, jak przebiega charakterystyka częstotliwościowa rezystorów. Oznaczenia na osi pionowej są dziwne – zobrazowana tu jest bowiem wartość współczynnika S21 w decybelach. Wartość ta informuje o module impedancji, a skala jest odwrócona, dlatego czym niżej przebiega charakterystyka – tym większa jest impedancja. Wraz z charakterystyką rezystora 470kΩ na tym samym rysunku niebieskim kolorem pokazany jest, powiedzmy w uproszczeniu – poziom szumów własnych przyrządu. Pokazuje on, że za pomocą najtańszej wersji NanoVNA do tej granicy można mierzyć impedancje (jest to charakterystyka zmierzona bez dołączania rezystora, odpowiadającą pomiarowi nieskończenie wielkiej impedancji). Do tych szczegółów jeszcze wrócimy.
Omówienie dwóch innych pożytecznych sposobów pomiaru impedancji trzeba zacząć od przypomnienia, że w NanoVNA mierzące parametr S11 gniazdo Ch0 współpracuje z mostkiem pomiarowym i dzięki temu jest zarówno wyjściem generatora, jak też wejściem selektywnego woltomierza w.cz. Natomiast gniazdo Ch1 mierzy parametr S21 i jest tylko wejściem drugiego selektywnego woltomierza. Rezystancja obu gniazd jest równa 50 omów.
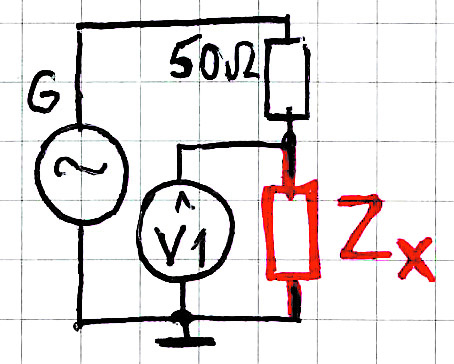
Jeżeli wykorzystujemy tylko gniazdko Ch0, to mogłoby się wydawać, że układ pomiarowy wygląda jak na rysunku 3.
Mamy wewnętrzną rezystancję wyjściową 50 omów i w szereg z nią włączamy badaną impedancję ZX. Mierzymy spadek napięcia na tej badanej impedancji, który jest proporcjonalny do wartości ZX, z uwzględnieniem amplitudy i fazy w stosunku do sygnału z generatora. Owszem, tak można byłoby mierzyć impedancję, ale w przypadku VNA tylko w pierwszym, bardzo dużym zgrubnym przybliżeniu od biedy można byłoby przyjąć taki model. Jeżeli chcemy rozpatrywać problem niepewności wyniku i dokładności, musimy uwzględnić obecność i specyfikę mostka pomiarowego (rysunek 4a), co pomijając pewne mniej ważne teraz szczegóły, prowadzi do uproszczonego schematu NanoVNA według rysunku 4b. Badana impedancja ZX jest jedną z gałęzi mostka.
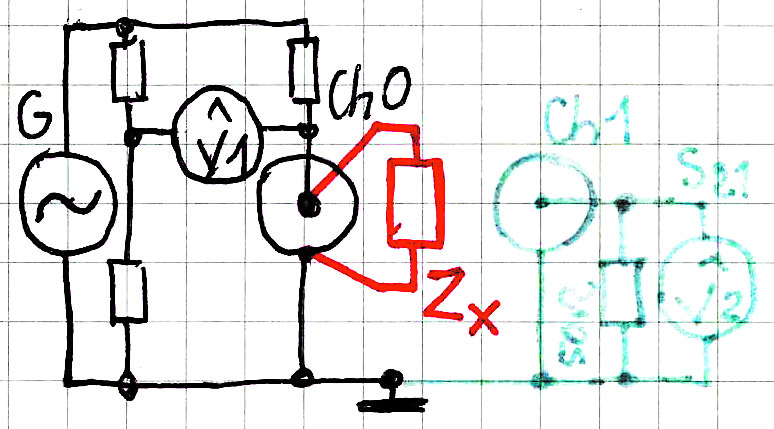
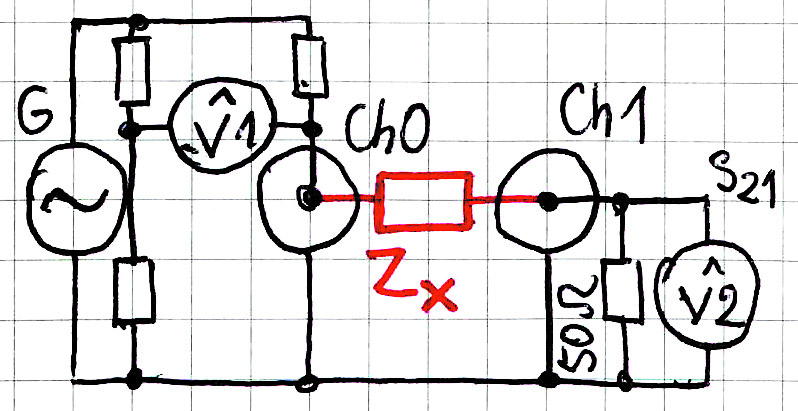
Bardzo interesujące nas dwa inne, równie proste sposoby pomiaru impedancji przedstawione są na rysunkach 5, 6.
Mamy trzy układy czy raczej konfiguracje pomiarowe, które są wykorzystywane odpowiednio do sytuacji, ponieważ każda ma inne zalety i wady. Aspekty praktyczne są omówione w następnym artykule MR094, natomiast dalsza część tego artykułu jest przeznaczona dla bardziej dociekliwych Czytelników, którzy nie tylko chcą mierzyć, ale też chcą rozumieć co, jak i dlaczego właśnie w ten sposób mierzą.
Tylko dla dociekliwych
Tak naprawdę, do pomiarów według rysunków 5 i 6 wykorzystujemy tylko wyniki z gniazda Ch1, które służy do pomiaru parametru S21. Sygnały na gnieździe Ch0 (i na mostku) też są wtedy automatycznie mierzone, ale ich nie wykorzystujemy.
W literaturze konfiguracja (sposób) pomiaru według rysunku 5 jest nazywana shunt-thru lub rzadziej shunt-through, natomiast konfiguracja z rysunku 6 jest nazywana albo series-through albo po prostu series. Najprostsza konfiguracja pomiarowa z rysunku 4, wykorzystująca współczynnik odbicia S11, nazywana bywa reflection albo shunt.
Dlaczego nie wystarczy prosty sposób z rysunku 4? Czy metody według rysunków 5, 6 są potrzebne i czy z jakiegoś powodu okazują się lepsze?
Najpierw zastanów się na tą sprawą samodzielnie, a dopiero potem czytaj dalej. To naprawdę ważna kwestia i najlepiej byłoby, gdybyś sam doszedł do właściwych wniosków. Dlatego zrób przerwę i zastanów się!
– – – – – – – – – – – – – – – – – – – – – – – – – – –
Z wcześniejszych informacji wiemy, że w przyrządzie NanoVNA mamy trzykanałowy przetwornik ADC o dużej rozdzielczości. To wskazywałoby na dużą dokładność i precyzję w bardzo szerokim zakresie mierzonych amplitud.
Tak, ale dokładność przetwornika ADC nie przekłada się wprost ani na dokładność pomiarów współczynnika odbicia oznaczonego S11, ani na dokładność pomiarów impedancji. Na bardzo uproszczonych rysunkach 4…6 mamy zaznaczone po dwa woltomierze. Jednak pomiar jest bardziej skomplikowany.
Otóż najprościej biorąc, przyrządy VNA dokonują pomiarów względnych. Mierzą współczynniki S11, S21, które w pierwszym uproszczeniu są stosunkami (zasadniczo impedancji, ale w rzeczywistości napięć). Nieprzypadkowo w NanoVNA wykorzystywane są trzy kanały przetwornika ADC i trzy miksery SA612, co daje trzy niezależne kanały pomiarowe. Dwa z nich rzeczywiście mierzą napięcia na gniazdach Ch0, Ch1, a trzeci jest kanałem odniesienia, niezbędnym przy realizowanych tu pomiarach względnych. Do dalszych obliczeń wykorzystywane są nie bezpośrednie wartości odczytane z pojedynczych kanałów przetwornika ADC, tylko stosunek wyników z danego kanału pomiarowego i kanału odniesienia. Do tego dochodzi jeszcze wzorcowa w pewnym sensie rezystancja o wartości 50 omów.
Sens tego wszystkiego staje się oczywisty, jeżeli weźmiemy pod uwagę, że S11 to współczynnik odbicia, więc jeżeli odbicia nie ma, czyli jest idealne dopasowanie, to S11 ma wartość 0. A odbicia nie ma tylko wtedy, gdy jest idealne dopasowanie, czyli gdy do gniazda Ch0 dołączona jest czysta rezystancja o wartości 50Ω. Najgorszy przypadek, czyli całkowity brak dopasowania i pełne odbicie, ma miejsce w dwóch przypadkach, gdy do gniazda Ch0 dołączona jest:
– Oporność (impedancja) równa zero omów – zwarcie.
– Oporność (impedancja) nieskończenie wielka – rozwarcie.
W obu przypadkach cały sygnał się odbija i współczynnik odbicia S11 wynosi wtedy 1 (dokładniej albo –1, albo +1).
Stwierdziliśmy, że VNA to odmiana omomierza, ale być może i Ciebie nurtuje ważne pytanie: co tak naprawdę mierzy analizator NanoVNA? I jak mierzy?
Otóż generalnie mierzy tylko dwa parametry: S11 – współczynnik odbicia oraz S21 – współczynnik transmisji. Współczynniki te określa, mierząc napięcia, a ściślej stosunki napięć. Uwzględnia przy tym nie tylko amplitudy, ale też przesunięcia fazy.
Potem, mając wartości S11, S21, obejmujące i ich wielkość, i przesunięcie fazy, a do tego rezystancję charakterystyczną 50Ω, z tych danych można wyliczyć mnóstwo innych parametrów, między innymi impedancję. I wiele takich pochodnych parametrów wylicza procesor w przyrządzie oraz poznany już program NanoVNA-Saver. Czyli omawiane teraz pomiary impedancji Z polegają na jej wyliczeniu ze zmierzonych wartości S11 i S21, które w przyrządzie są określane jako stosunki napięć.
Te ważne informacje jak na razie nie dały odpowiedzi, dlaczego sposoby pomiaru z rysunków 5 i 6 miałyby być lepsze niż najprostszy sposób według rysunku 4.
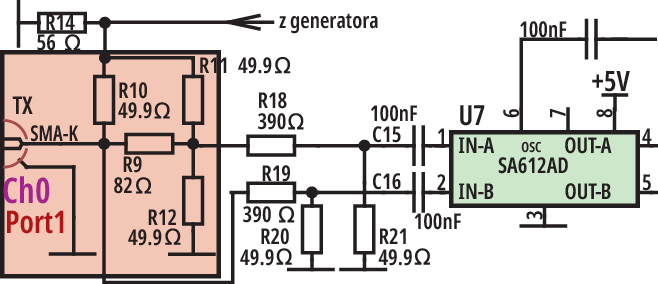
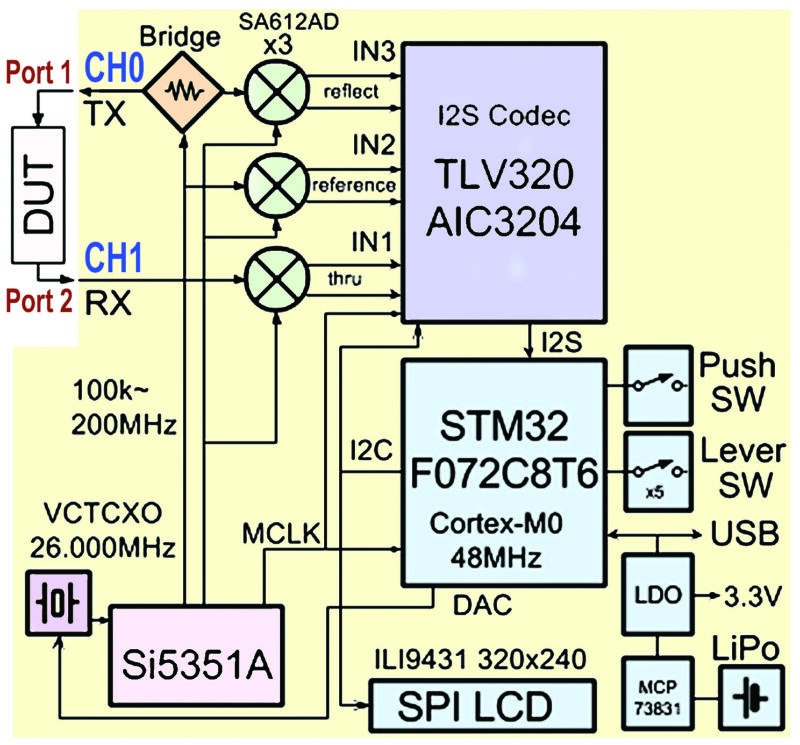
W kwestii dokładności i niepewności wyniku przy pomiarach impedancji kluczowe jest to, że zaznaczone na bardzo uproszczonych rysunkach 4…6 woltomierze reprezentują wynik pomiaru względnego – stosunek wartości z kanału pomiarowego i kanału odniesienia, co po części widać na schemacie blokowym NanoVNA (rysunek 7), gdzie mamy tor odniesienia – reference, i co odpowiada definicji parametrów S11, S21.
I pomału dochodzimy do sedna problemu dokładności: sam przetwornik ADC (TLV320AIC3204) ma bardzo szeroki zakres dynamiki (rzędu 100dB), ale też w obu kanałach nieuchronnie występują jakieś błędy.
Oczywiście dokładność pomiarów jest pogorszona, gdy sygnał w kanale pomiarowym jest bardzo, bardzo mały, na poziomie szumów. Wprawdzie stosunek wielkości jest wtedy „wyraźny”, jednak szumy wprowadzają stosunkowo duże błędy. Poziom szumów własnych jest oczywistym i podstawowym ograniczeniem, a NanoVNA ma pod tym względem kiepskie właściwości. Sam przetwornik ADC na dynamikę rzędu 100dB, ale finalnie NanoVNA ma dynamikę mniejszą niż 80dB.
Mniej oczywisty jest inny ważny szczegół, dotyczący pomiarów względnych. Otóż jeżeli w kanale pomiarowym sygnał jest znacząco mniejszy od sygnału w kanale odniesienia, to stosunek wielkości tych sygnałów jest dobrze, wyraźnie określony. Gdy jednak stosunek wielkości sygnału z gniazda i sygnału odniesienia będzie bardzo bliski jedności, wtedy też łatwo o błędy.
Specyfiką VNA jest to, że mierzymy stosunki napięć, dlatego problem niepewności wyniku występuje także wtedy, gdy w kanale pomiarowym sygnał będzie prawie taki sam, jak w kanale odniesienia. Do dalszej obróbki przekazywany jest właśnie stosunek wartości z dwóch kanałów i różne błędy w kanałach spowodują, że dokładność bardzo się obniża, gdy w kanale pomiarowym i odniesienia wielkości sygnałów są zbliżone.
I właśnie dlatego dokładność pomiarów jest najlepsza, gdy według rysunku 4 mierzone są impedancje zbliżone do nominalnej 50Ω. Niepewność wyniku zwiększa się, zarówno przy znaczącym zwiększeniu, jak i zmniejszeniu impedancji względem 50Ω, bowiem wtedy współczynnik S11 jest bardzo bliski jedności.
Co istotne, tak jest nie tylko w taniutkim NanoVNA, ale generalnie we wszystkich analizatorach VNA, nawet tych najkosztowniejszych. Oczywiście są różnice w zakresie dokładności i dynamiki, ale opisywany właśnie problem dotyczy metody, a nie tylko taniego NanoVNA.
Jeszcze raz wracamy do rysunku 4. Wiemy już, że „wewnętrzny woltomierz” oznaczony V1 dobrze radzi sobie z niewielkimi sygnałami, a takowe wystąpią na przekątnej mostka tylko wtedy, gdy mostek będzie niedaleki od równowagi, czyli gdy badana impedancja Zx nie będzie się zdecydowanie różnić od 50Ω. Wtedy napięcie na przekątnej mostka będzie nieduże, mniejsze od wielkości sygnału odniesienia. Natomiast i przy bardzo małej wartości impedancji Zx, jak i przy bardzo dużej na przekątnej mostka w obu przypadkach wystąpi duże napięcie, bliskie maksymalnemu. A przyrząd bardzo słabo radzi sobie w takich przypadkach, bo stosunek wielkości sygnałów w torze pomiarowym i w torze odniesienia jest wtedy bliski jedności.
Mamy tu niezbyt precyzyjne obrazowe uzasadnienie, dlaczego przy wykorzystaniu tylko gniazda Ch0 służącego do pomiaru S11 dobrą dokładność uzyskamy tylko wtedy, gdy wartość badanej impedancji Zx niezbyt dużo będzie różnić się od nominalnej 50 omów.
A czy potrafiłbyś samodzielnie przedstawić podobne obrazowe uzasadnienie dotyczące metod z rysunków 5 i 6? To nie jest trudne!
Zrób przerwę w czytaniu i spróbuj!
– – – – – – – – – – – – – – – – – – – – – – – – – – –
W przypadku pomiarów według rysunków 5 i 6 wykorzystujemy tylko wartość parametru S21, czyli stosunek napięcia sygnału na porcie – gnieździe Ch1 i napięcia odniesienia. Także i tu dokładność jest pogorszona, gdy napięcia są zbliżone, czyli gdy współczynnik S21 jest bliski jedności.
Inaczej mówiąc, także przy pomiarze S21 przyrządy VNA słabo radzą sobie przy największych możliwych sygnałach, a dobrze radzą sobie przy niewielkich sygnałach (ale nie za bardzo małych, takich na poziomie szumów). Wracamy do rysunku 5: przy jakich wartościach impedancji Zx na wejściu Ch1 sygnał będzie średni lub mały, ale nie bliski maksymalnemu?
Oczywiście badana impedancja Zx powinna być mniejsza od rezystancji charakterystycznej 50Ω – może być dużo, dużo mniejsza, bowiem dynamika NanoVNA to jednak kilkadziesiąt decybeli, a przykładowo 60dB to stosunek napięć równy 1000.
Oznacza to, że konfiguracja z rysunku 5 dobrze nadaje się do pomiaru małych impedancji, mniejszych od 50Ω.
Odwrotnie jest w szeregowej konfiguracji z rysunku 6. Gdyby impedancja Zx była mała, to woltomierz V1 zmierzyłby duży sygnał, bliski maksymalnemu. Aby z małym błędem mierzył małe sygnały, impedancja Zx powinna być większa od 50Ω – może być wielokrotnie większa. Wniosek: konfiguracja z rysunku 6 dobrze nadaje się do pomiaru dużych impedancji, większych od 50Ω.
To było obrazowe, intuicyjne wyjaśnienie, bardzo uproszczone. Jeszcze raz podkreślam, że problem niepewności/dokładności pomiarów dotyczy nie tylko NanoVNA, ale też wszystkich przyrządów VNA, także najdroższych. Ściślej biorąc, w grę wchodzi też dokładność używanego przyrządu VNA, jednak niezależnie od tego możemy mówić o błędzie metody czy błędzie konfiguracji.
Zapamiętaj, że VNA jako podstawowe wielkości mierzy parametry S11 i S21 na podstawie stosunku napięć jednego z dwóch torów pomiarowych i napięcia odniesienia. Wartości S11 i S21 to niejako „wyniki podstawowe”, z których procesor wylicza liczne inne wielkości, w tym właśnie (wektorową) wartość dołączonej impedancji.
Rysunek 8 pokazuje sposób obliczania impedancji w oparciu o S11 i S21 oraz informacje o błędach i zalecane zakresy pomiarowe. Poszczególne źródła podają wprawdzie nieco inne wartości graniczne poszczególnych zakresów, ale to nie jest problem.
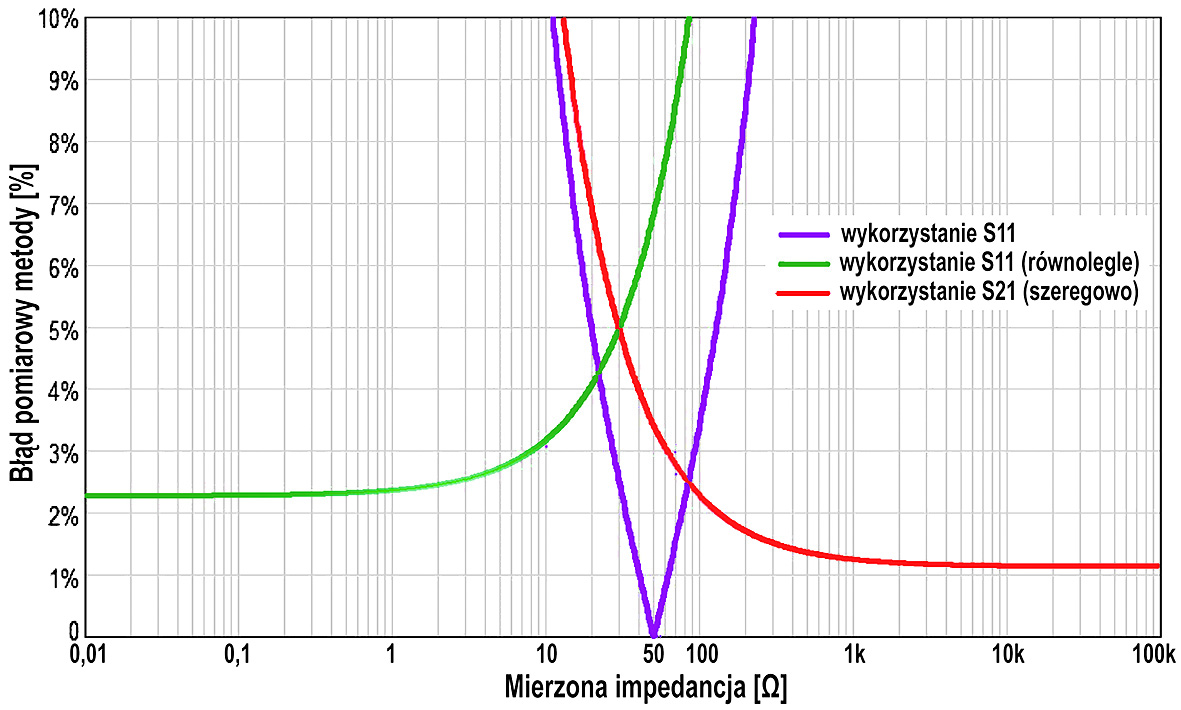
Problemem jest to, że dla praktyka zupełnie nieprzyswajalne są pokazane na rysunku 8 zależności dotyczące niepewności i spodziewanych błędów. Rzeczywiście, są to bardzo zaawansowane szczegóły, a przy matematycznym wyprowadzaniu tych zależności trzeba wykorzystać tak zwany jakobian. Nie będziemy zagłębiać się w zawiłości związane z niepewnością wyniku. Sedno problemu zdecydowanie lepiej widać po naniesieniu tych dziwnych zależności na wykres, co pokazuje rysunek 9 (według materiałów MWRF). Nie wchodząc w szczegóły: na osi pionowej pokazana jest spodziewana wielkość błędu w zależności od mierzonej impedancji.
To jest bardzo ważna kwestia: pomiaru impedancji za pomocą analizatora VNA należy dokonywać w tej konfiguracji z rysunków 4, 5, 6, która zapewnia mniejszą niepewność, czyli mniejsze błędy.
Do wstępnych pomiarów można wykorzystywać konfigurację według rysunku 4 z wykorzystaniem S11.
Natomiast przy dokładniejszych pomiarach impedancji kondensatorów wykorzystamy układ shunt-through według rysunku 5, bowiem najbardziej interesuje nas wtedy minimalna impedancja, równa rezystancji wewnętrznej ESR. Z kolei przy pomiarze cewek (dławików) zwykle wykorzystamy konfigurację series-through według rysunku 6, ponieważ interesuje nas rezonans własny i jego częstotliwość, a wtedy dławik ma maksymalną impedancję (w postaci czystej rezystancji).
W kolejnym artykule MR094 omówiono bardziej praktyczne aspekty zagadnienia.
Piotr Górecki