Elektronika (nie tylko) dla informatyków (2) Rezystory
W poprzednim wykładzie zaznajomiliśmy się z takimi pojęciami jak napięcie i prąd elektryczny oraz energia i moc. W tym odcinku zapoznamy się z najpopularniejszymi elementami elektronicznymi czyli rezystorami.
Rezystor jaki jest – każdy widzi… Rezystory, zwane też opornikami, są niewątpliwie najpopularniejszymi elementami elektronicznymi. Zasadniczo ich działanie jest bardzo proste. Ale nie znaczy to, że należy je lekceważyć. W niektórych zastosowaniach to właśnie rezystory mają kluczowy wpływ na właściwości urządzenia. Każdy bez wyjątku elektronik powinien dobrze rozumieć podstawowe parametry rezystorów, ale dobrze byłoby mieć przynajmniej ogólne pojecie także o specyficznych właściwościach, ważnych w zastosowaniach, w których wymagana jest precyzja.
W podręcznikach przeczytasz, że rezystory dzielą się na drutowe, masowe, metalizowane, tlenkowe, kompozytowe, cementowe, itd.
Dziś drutowe są tylko rezystory dużej mocy, powyżej 2 W. Natomiast ogromna większość małych to albo rezystory węglowe (carbon resistors), albo rezystory metalizowane (metal resistors). W obu typach na porcelanowym wałeczku nałożona jest warstwa oporowa, a na to lakier ochronny – patrz fotografia 1. Często czynna warstwa rezystora jest nacięta i ma w sumie postać spirali, a ściślej helisy. Rezystory węglowe mają znacznie gorsze parametry od metalizowanych (metalowych). Zacznijmy jednak od tego, że dla hobbysty praktyka kluczowe znaczenie mają trzy podstawowe parametry rezystora:
1 – rezystancja nominalna
2 – tolerancja
3 – obciążalność (moc).
Zanim je omówimy, warto przypomnieć podstawy teoretyczne.
Łyk teorii dla początkujących
Nazwy: rezystor i opornik związane są z faktem, że element ten istotnie przeciwstawia się przepływowi prądu. Często mówi się, że rezystory służą do ograniczania prądu, co tylko po części jest prawdą. W niektórych zastosowaniach nie tyle ograniczają, co umożliwiają przepływ prądu. Ponadto rezystory często pracują w dzielnikach napięcia oraz pełnią istotne role, np. w generatorach i filtrach.
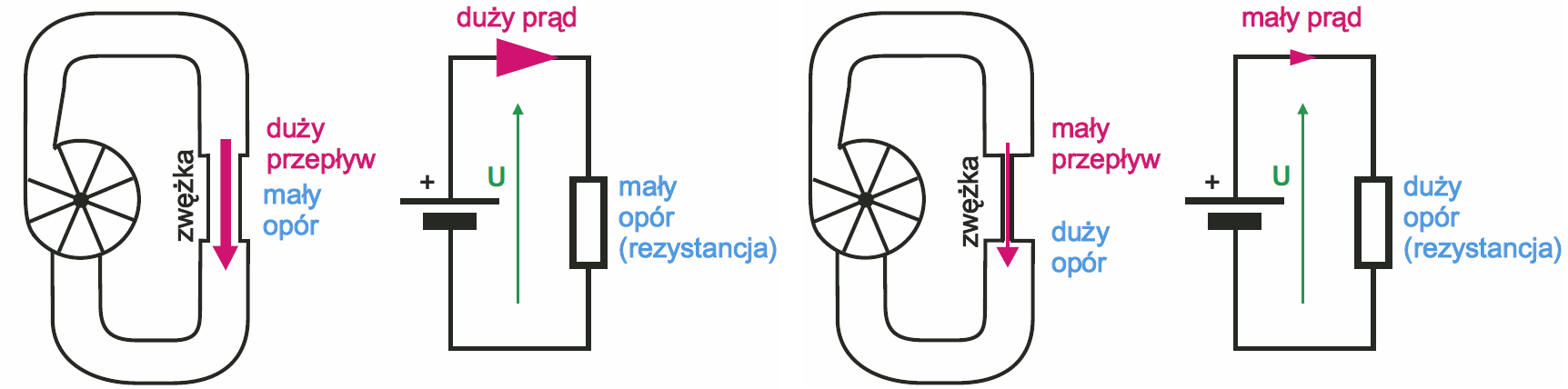
Działanie rezystora można dobrze zilustrować w zaproponowanej wcześniej analogii wodnej. Otóż w instalacji wodociągowej panuje pewne ciśnienie. Ciśnienie to może spowodować przepływ wody. Jak mówiliśmy w poprzednim odcinku, ciśnienie wody jest odpowiednikiem napięcia elektrycznego, natomiast przepływ wody jest odpowiednikiem prądu elektrycznego. W instalacji wodociągowej, czyli w obwodzie hydraulicznym, odpowiednikiem rezystora jest najzwyczajniejsza zwężka. Czym mniejszy przekrój zwężki, tym większy jest jej opór dla przepływającej wody. Zwyczajny zawór pozwala regulować przepływ, czyli jest elementem, którego opór można płynnie regulować. Zamknięty zawór ma nieskończenie wielką oporność, bo zmniejsza przepływ wody do zera. Odpowiednikiem elektrycznym jest przerwa, brak obciążenia, a właściwie nieskończenie wielka oporność obciążenia.
Rysunek 2 ilustruje podstawową, oczywistą zależność dla obwodu hydraulicznego i co ważniejsze – elektrycznego. Przy okazji ilustruje fundamentalne prawo elektroniki, prawo Ohma.
Czym większa oporność przy danym napięciu (ciśnieniu), tym mniejszy prąd (przepływ). Ponadto, co oczywiste, dla danej rezystancji (zwężki), czym większe napięcie (ciśnienie), tym większy prąd (przepływ wody). Reprezentuje to wzór:
![]()
gdzie R to symbol oporności, dokładniej rezystancji. Zapamiętaj, że oporność (rezystancja) to zdolność do przeciwstawiania się przepływowi prądu i że jest to też współczynnik proporcjonalności między napięciem a prądem. Jeśli znamy wartości napięcia i prądu, możemy obliczyć opór:
![]()
A znając prąd i opór, możemy wyliczyć napięcie:
![]()
Tu warto wspomnieć o dwóch przypadkach szczególnych. Oczywiste jest, że jeśli np. do baterii nie jest dołączone żadne obciążenie, to prąd nie płynie. Nie masz wątpliwości, że jeśli napięcie jest, a prądu nie ma, to oporność jest nieskończenie wielka. To jest jasne, choć ściśle biorąc, często oporność nie jest nieskończona, a po prostu ma niemierzalnie dużą wartość, przez co prąd jest niemierzalnie mały.
A czy możliwa jest sytuacja, że prąd płynie, a napięcia nie ma? Tak! Taka sytuacja zachodzi w tzw. nadprzewodnikach, których oporność jest równa zeru. Z nadprzewodnikami nie mamy do czynienia na co dzień, ponieważ póki co, w znanych materiałach efekt nadprzewodnictwa występuje tylko w bardzo niskich temperaturach.
A teraz wspomnijmy o pewnym fałszywym wyobrażeniu. To dość istotna sprawa.
Przyczyna i skutek?
Trzy podane wcześniej zależności: I = U/R, R = U/I, U = I×R to wzory najczęściej wykorzystywane przez elektroników. Nie warto byłoby tego przypominać, gdyby nie fakt, iż część hobbystów ma pewien kłopot z zależnością wyrażaną przez wzór U = I×R. Na pewno jest to przekształcony matematycznie „podstawowy” wzór wyrażający prawo Ohma: I = U / R. Jednak nie chodzi tu tylko o teorię, ale też o wyobrażenia istotne w praktyce. Otóż początkującym elektronikom niesłusznie wydaje się, że zawsze napięcie jest przyczyną, a prąd – skutkiem, jak mógłby sugerować „podstawowy” wzór I = U / R. Taki wniosek może nasuwać choćby prosty przykład z baterią: przez rezystor płynie prąd dopiero wtedy, gdy zostanie on dołączony do baterii. Wydaje się, że napięcie jest przyczyną, a skutkiem – przepływ prądu.
Takie wyobrażenie jest jednak błędne. Czy czujesz, że zgodnie ze wzorem U = I×R, to przepływ prądu może być przyczyną, a skutkiem będzie wtedy napięcie na rezystorze?
Niestety, wielu początkujących nie dopuszcza do siebie wyobrażenia, iż to prąd jest przyczyną, a napięcie – skutkiem. Jeśli i Ty masz z tym kłopot, dokładnie przeanalizuj dalszy opis i spróbuj zrozumieć pojęcie źródła prądowego. Szczerze mówiąc, mówienie o skutku i przyczynie jest nieścisłe. Należałoby raczej powiedzieć, że napięcie i prąd są nierozłącznie związane opornością obwodu. Jednak w wielu przypadkach wyobrażenie, iż to prąd jest przyczyną, a napięcie skutkiem, może znakomicie ułatwić zrozumienie zasad działania elementów i układów.
Wniosek, że to napięcie jest przyczyną, a prąd skutkiem, wynika głownie z tego, że w życiu codziennym często mamy do czynienia ze źródłami napięciowymi. Idealne źródło napięciowe to element, w którym napięcie wyjściowe jest niezmienne, niezależne od oporności obciążenia i płynącego prądu. Natomiast prąd zależy od oporności dołączonego obciążenia według zależności I = U/R. Właściwości źródła napięciowego ma bateria, zasilacz, a zwłaszcza duży akumulator (którego napięcie bardzo mało zależy od prądu obciążenia) – patrz fotografia 3.
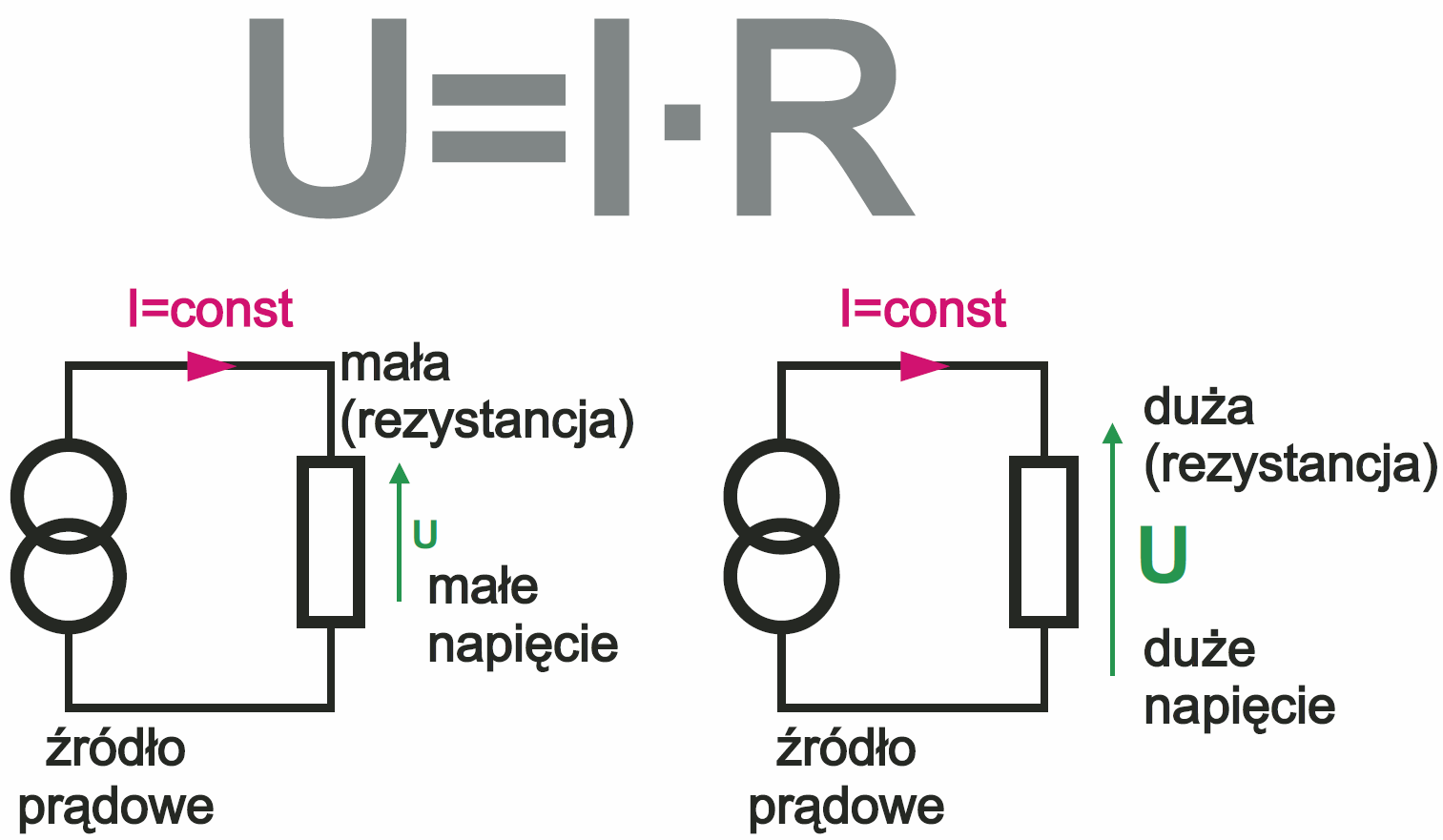
Natomiast w życiu codziennym prawie nigdy, albo wręcz nigdy, nie mamy do czynienia z tak zwanymi źródłami prądowymi. Tymczasem niektóre elementy elektroniczne, w tym tranzystory, zachowują się nie jak źródła napięciowe, tylko jak źródła prądowe. Idealne źródło prądowe to taki dziwny twór, w którym prąd wyjściowy jest niezmienny, a napięcie na obciążeniu zależy od oporności obciążenia właśnie według wzoru U = I×R. Ilustruje to rysunek 4 (przy czym w książkach na schematach spotyka się rozmaite symbole graficzne źródła prądowego).
Podane wnioski mogą być o tyle trudne do intuicyjnego zaakceptowania, że na zaciskach takiego źródła prądowego przy braku obciążenia, czyli przy oporności nieskończenie wielkiej, napięcie wyjściowe też powinno być… nieskończenie wielkie (U=I×R). Z kolei przy rezystancji obciążenia równej zeru, czyli przy zwarciu, napięcie źródła prądowego będzie po prostu równe zeru.
Jeśli nie bardzo Ci to trafia do przekonania, spróbuj porównać źródło napięciowe z „odwrotnym” źródłem prądowym i uchwycić analogię. Przecież teoretyczne biorąc, idealne źródło napięciowe przy oporności obciążenia równej zeru powinno dać nieskończenie wielki prąd. Oczywiście w praktyce tak nie będzie, bo nawet wielki akumulator, który jest bardzo dobrym źródłem napięciowym, nie może dać nieskończenie wielkiego prądu. To wydaje się naturalne. Podobnie rzeczywiste źródło prądowe nie może zwiększyć napięcia na swych zaciskach do nieskończenie wielkiej wartości. Według definicji, w idealnym źródle napięciowym napięcie wyjściowe nie zależy od obciążenia; analogicznie w źródle prądowym prąd wyjściowy nie zależy od obciążenia. Pamiętaj też, że pojęcia źródła napięciowego i prądowego to jedynie teoretyczne, wyidealizowane modele. Niestety, nie mogę Ci podać dobrego przykładu źródła prądowego (w analogii hydraulicznej odpowiednikiem źródła prądowego byłaby pompa o stałej wydajności, ale to chyba nie jest pomoc w zrozumieniu omawianej kwestii).
Pomimo braku przykładu, spróbuj przyswoić sobie pojęcie źródła prądowego, w którym prąd wyjściowy nie zależy od obciążenia, a napięcie zależy od obciążenia zgodnie ze wzorem U = I×R. Jeśli do tej pory było to dla Ciebie obce, jeszcze raz przeanalizuj powyższy akapit i rysunek 4. Choć przeciętny śmiertelnik nie ma na co dzień do czynienia ze źródłami prądowymi, to inaczej jest z elektronikami. Bo na przykład tranzystory w pewnych warunkach zachowują się właśnie jak (nieidealne) źródła prądowe.
Prawa Kirchhoffa i inne
Przy okazji przypomnijmy kolejne bardzo ważne prawa i zasady elektroniki. Są one bardzo proste i oczywiste, ale trzeba je przypomnieć:
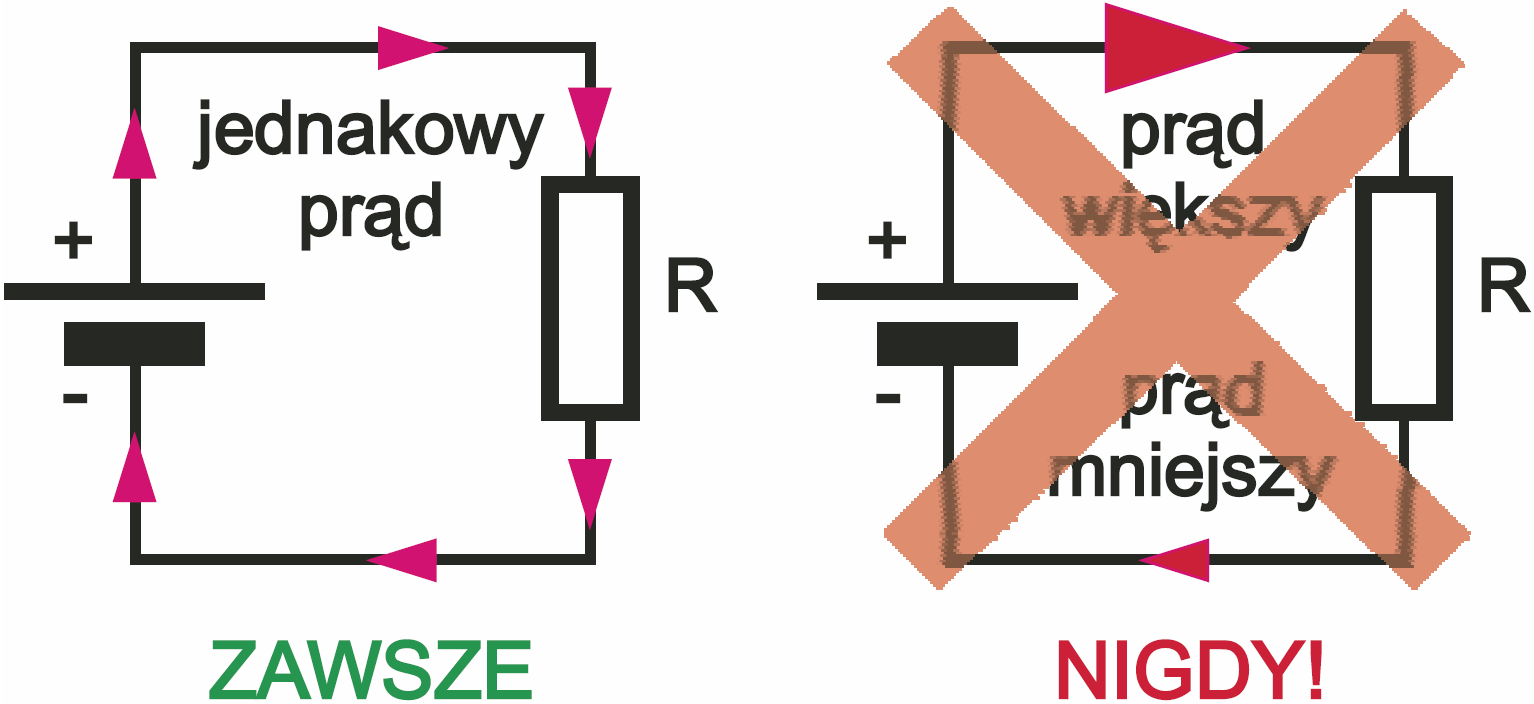
To jasne, że podobnie jak woda nie wyparuje z rur, także prąd nie może „zawieruszyć się gdzieś po drodze”. Po pierwsze prąd nie może zmniejszyć swej wartości, jak pokazuje rysunek 5.
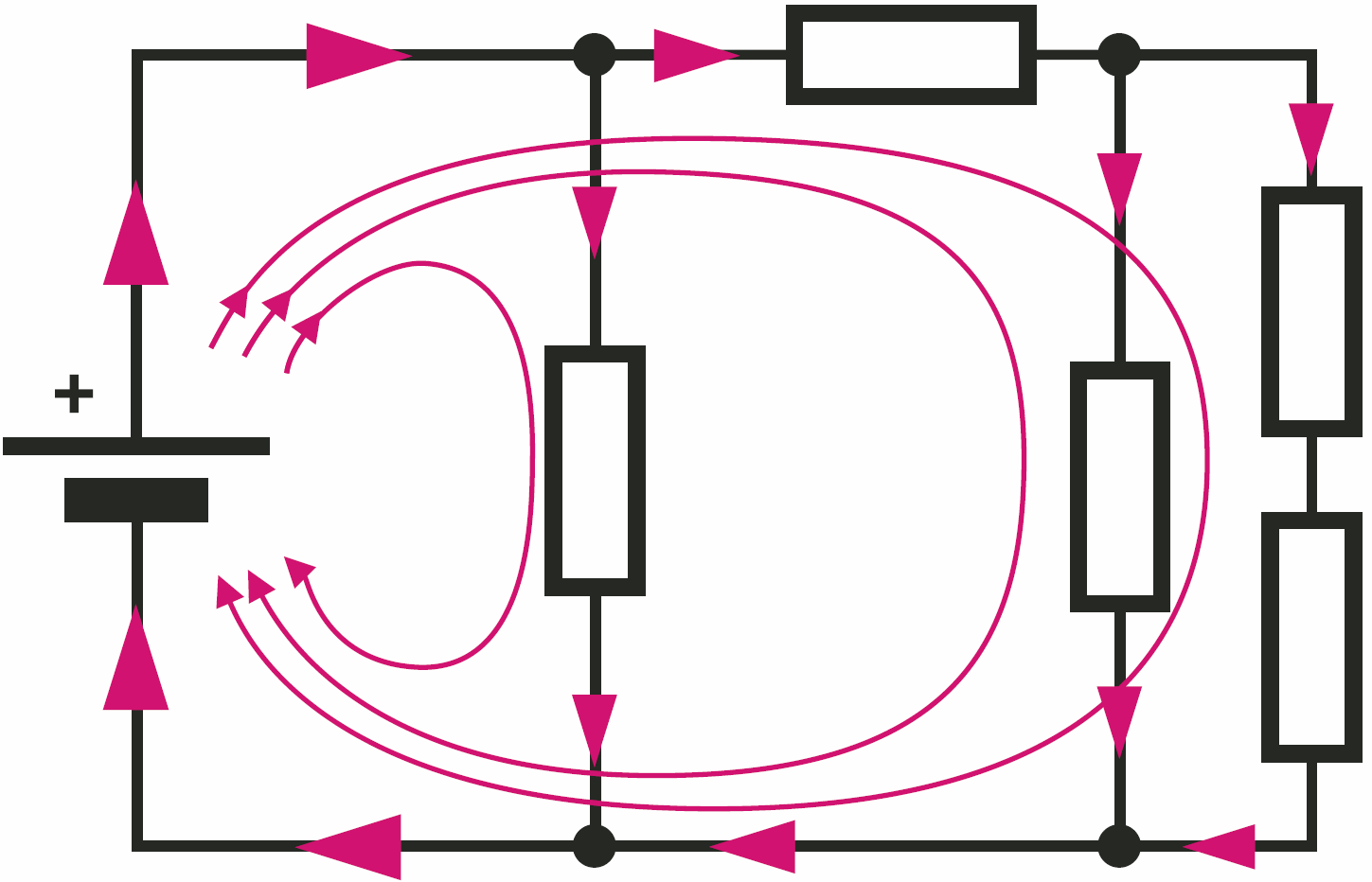
Czy wiesz, że prądy zawsze płyną w zamkniętych obwodach? Zawsze do ujemnego bieguna baterii (źródła zasilania) wpływa/powraca taki sam prąd, jaki wypływa z dodatniego bieguna – ilustruje to rysunek 6.
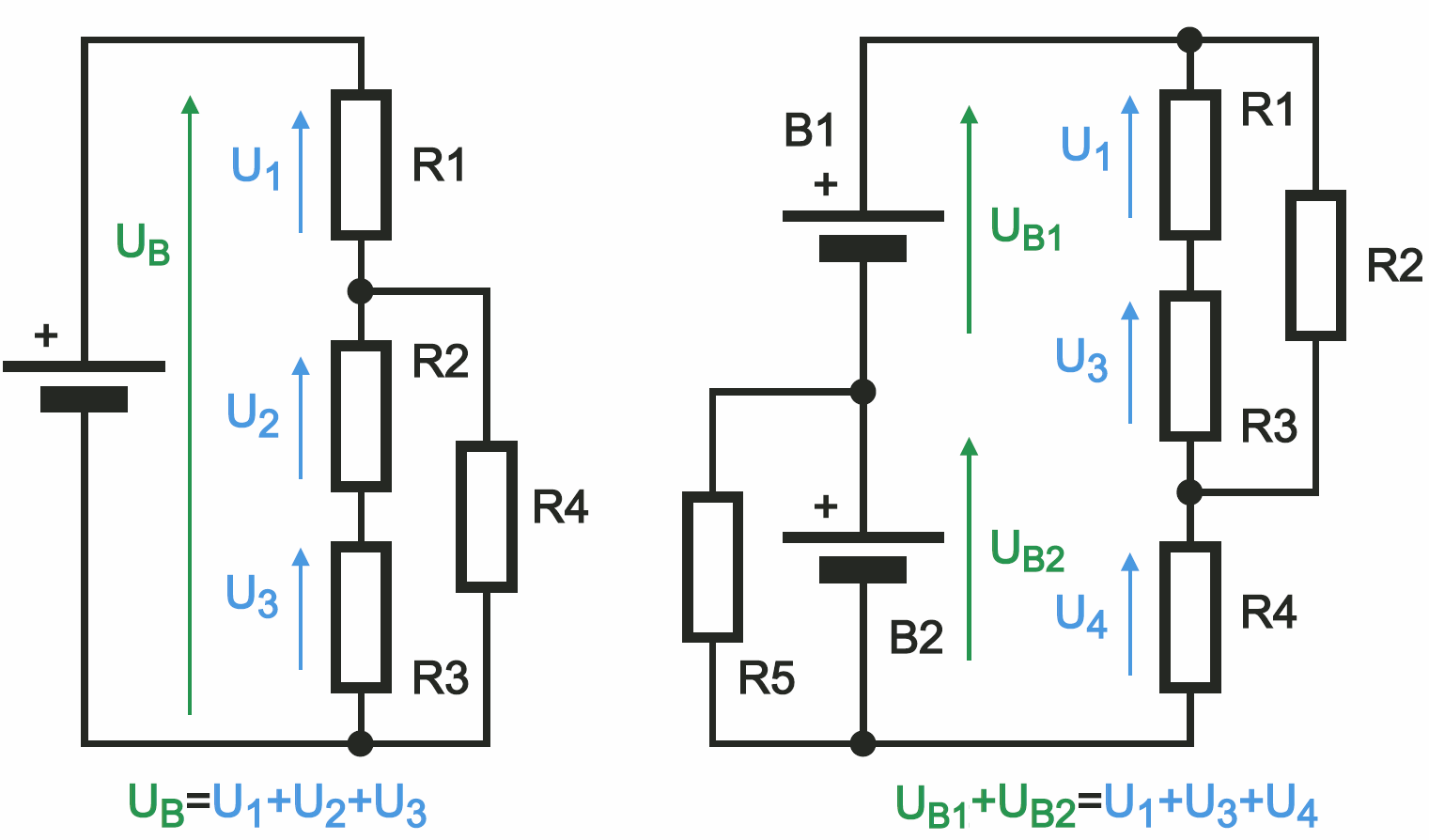
Po drugie, podobnie jak w obwodzie hydraulicznym, w danym węźle suma prądów wpływających zawsze jest równa sumie prądów wypływających. Inaczej mówiąc, suma prądów w danym węźle jest równa zeru – i to jest treść prądowego prawa Kirchhoffa. Podobnie jak nie może „zaginąć” prąd, tak też nie może zniknąć napięcie. Definicja, a właściwie napięciowe prawo Kirchhoffa mówi, że suma napięć w oczku jest równa zeru. My nie będziemy wgłębiać się w szczegóły. Możemy w uproszczeniu stwierdzić, że suma napięć na obciążeniach jest równa napięciu źródła. Rysunek 7 ilustruje te oczywiste prawa.
Przy okazji przypominam, że na schematach zaznaczamy kierunek przepływu prądu od bieguna dodatniego baterii, przez obciążenie do bieguna ujemnego. Natomiast napięcia oznaczamy strzałkami, przy czym grot strzałki pokazuje wyższy, czyli bardziej dodatni potencjał.
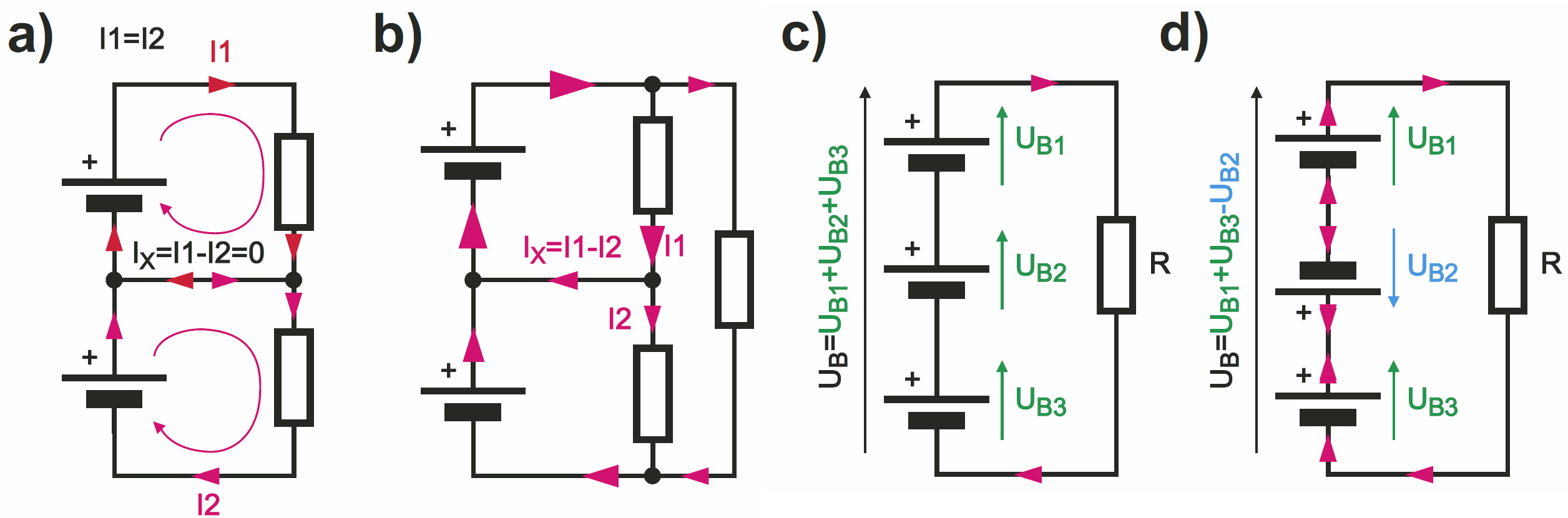
Czasem sytuacja jest bardziej skomplikowana. Gdy występuje kilka źródeł napięcia, przy analizie trzeba brać pod uwagę wypadkową prądów – gdy prądy płyną w przeciwnych kierunkach, to ich wartości się odejmują – rysunki 8a i 8b. A jeśli chodzi o napięcia, to mogą się dodawać lub odejmować – rysunki 8c i 8d.
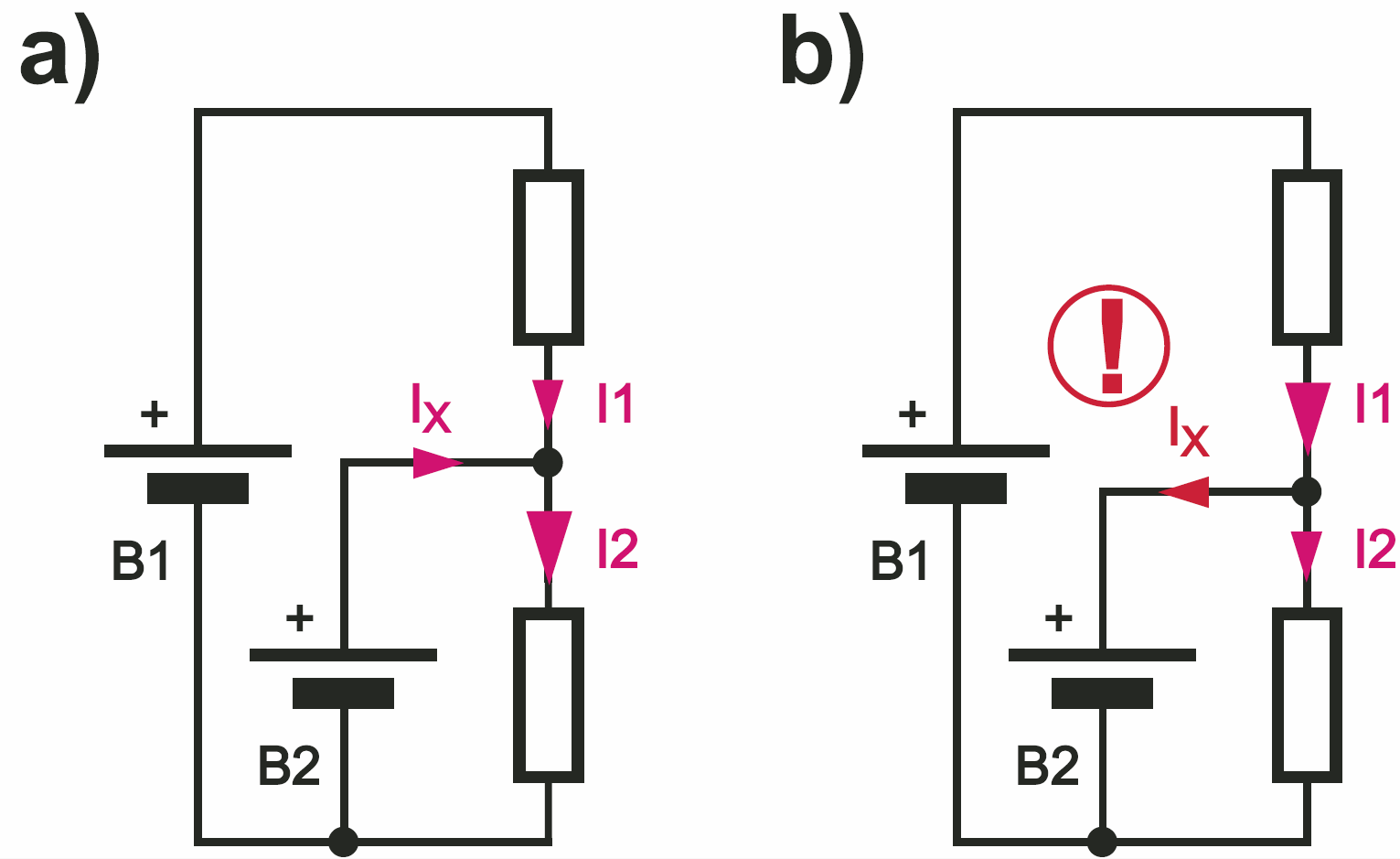
Obecność kilku źródeł może też spowodować inne nieoczekiwane konsekwencje. Przykład pokazany jest na rysunku 9. Kierunek prądu Ix zależy od napięć obu źródeł i wartości R1 i R2.
W sytuacji z rysunku 9a wszystko jest oczywiste – można powiedzieć, że z obu źródeł wypływa prąd i zarówno B1, jak i B2 są źródłami energii. Natomiast w przypadku z rysunku 9b wygląda na to, że B2 nie jest już źródłem energii, ponieważ prąd Ix ma „niewłaściwy” kierunek. Łatwo sobie wyobrazić taką sytuację, gdy B2 jest akumulatorem – wtedy po prostu akumulator jest ładowany prądem Ix i nic szczególnego się nie dzieje. Ale nie zawsze B2 jest akumulatorem – wtedy wszystko zależy od właściwości tego realnego źródła, zwłaszcza od tego, czy w ogóle prąd może wpływać do źródła. Zwłaszcza w przypadku niektórych stabilizatorów i zasilaczy (ale też baterii jednorazowych) niemożliwe jest „ładowanie” znaczącym prądem i wtedy w sytuacji z rysunku 9b napięcie U2 rośnie, a źródło B2 może zostać niejako „odcięte”, jakby go nie było.
Podobny problem występuje też w sytuacji z rysunku 8d, gdzie źródło B2 jest włączone „odwrotnie”.
To są jednak dość specyficzne zagadnienia, w które nie będziemy się wgłębiać.
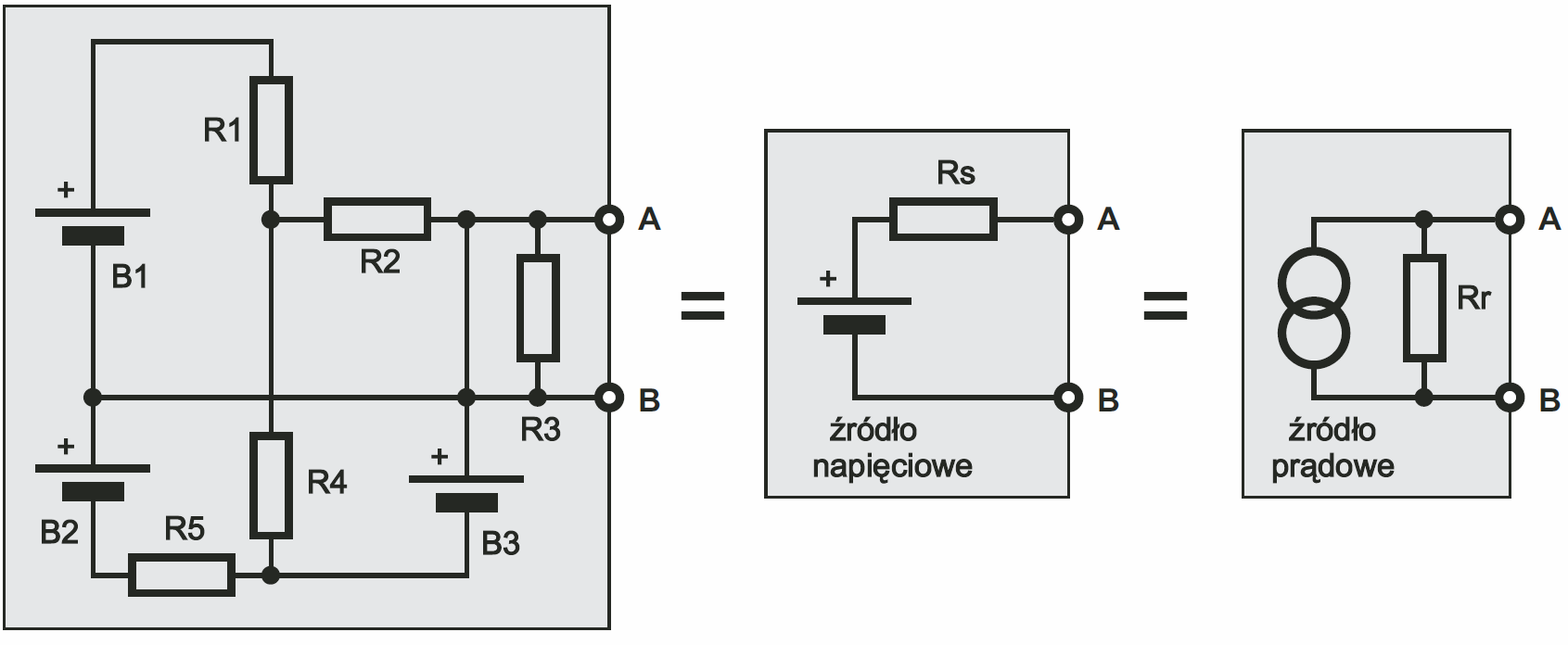
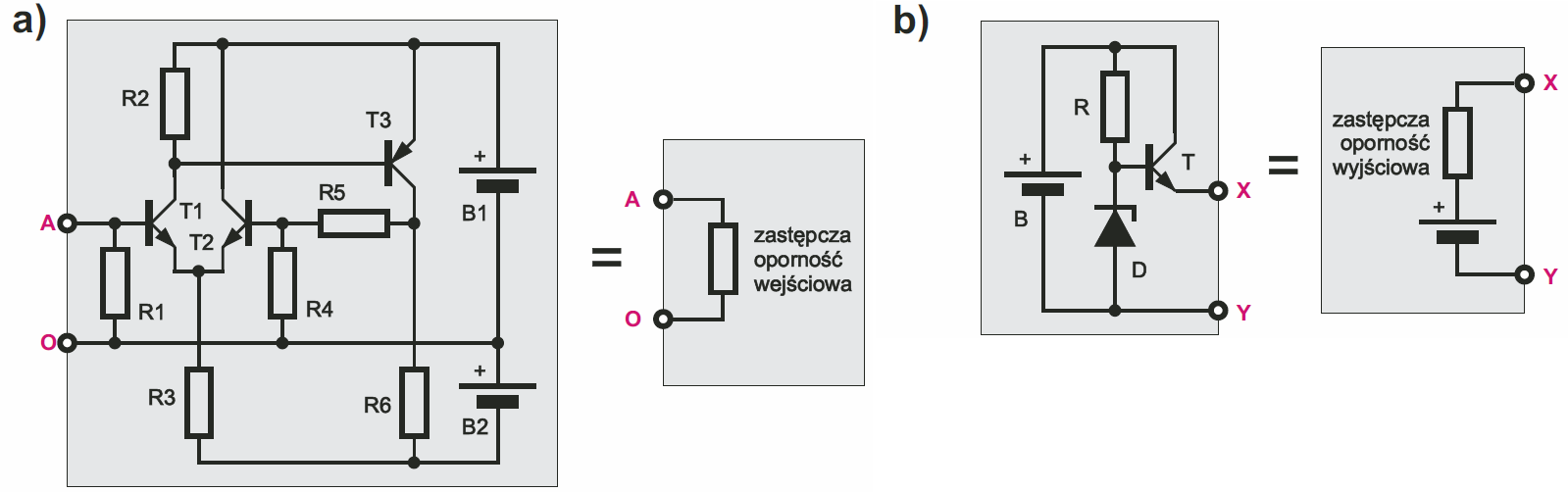
Musimy za to poruszyć inną istotną sprawę. Otóż bardzo często nie interesują nas wszystkie detale, jak działa i zachowuje się dany obwód czy układ. Ważne jest tylko „jak jest widziany z zewnątrz”. Dany obwód traktujemy jako „czarną skrzynkę” i wręcz nie chcemy znać szczegółów. Ilustruje to trochę sztuczny przykład z rysunku 10. Okazuje się, że nawet skomplikowane obwody można zastąpić albo szeregowym połączeniem źródła napięciowego i szeregowej rezystancji, albo źródła prądowego i równoległej rezystancji o odpowiednio dobranych parametrach. Właśnie streściłem Ci tu twierdzenia Thevenina i Nortona, a w szczegóły i wyjątki nie będziemy wnikać.
Dodam tylko, że nie jest to jakaś nieprzydatna teoria. Wprost przeciwnie. W praktyce najczęściej chodzi jeden z dwóch przypadków:
a – zastępczą oporność wejściową,
b – zastępczą oporność wyjściową.
Rysunek 11 pokazuje dwa uproszczone przykłady. Może nasunie się Ci pytanie: a jak obliczyć takie oporności? Otóż precyzyjne obliczenie oporności zastępczej złożonych układów byłoby dość trudne i wymagałoby rozwiązania zestawu równań, zwłaszcza tam, gdzie oporności zmieniają się zależnie od przetwarzanych sygnałów (napięć i prądów), czyli gdy mamy do czynienia z tzw. opornościami nieliniowymi. Dlatego w praktyce bardzo często obliczamy, a właściwie tylko szacujemy z grubsza, przybliżone wartości oporności zastępczej (wypadkowej). Do takich uproszczonych obliczeń zwykle potrzebne są wzory na rezystancję zastępczą równolegle połączonych oporników. Do tej sprawy jeszcze wrócimy.
Na razie powinieneś zapamiętać, że bardzo często w praktyce mówimy o oporności (zastępczej) widzianej od strony jakichś dwóch punktów, jak w przykładzie z rysunku 11a.
Oporność oporności nierówna
Choć opornik i rezystor to dwie równorzędne nazwy tego samego elementu, to oporność i rezystancja nie zawsze mogą być stosowane wymiennie.
Oporność to określenie bardzo szerokie, ogólne i nieprecyzyjne. Prawdopodobnie już spotkałeś się z takimi określeniami jak impedancja czy reaktancja. Można powiedzieć, że to też są odmiany oporności. Impedancja to inaczej oporność zespolona, reaktancja to oporność bierna, natomiast rezystancja to oporność czynna.
Problem w tym, że liczne elementy elektroniczne inaczej zachowują się przy napięciu/prądzie o niezmiennej wartości, a inaczej, gdy wartość napięcia czy prądu zmienia się w czasie. Wrócimy do tych szczegółów przy omawianiu kondensatorów i cewek. Choć nie jest to do końca prawdą, na razie możesz przyjąć, że rezystancja, czyli oporność czynna, dotyczy napięcia/prądu o niezmiennej wartości, czyli napięcia/prądu stałego.
Zapamiętaj, że wszystkie trzy podane rodzaje oporności wyrażamy w omach (od nazwiska niemieckiego fizyka Georga Simona Ohma). Oporność 1 oma ma opór, w którym napięcie 1 wolta wywołuje przepływ prądu 1 A: 1 Ω = 1 V / 1 A
Nominał, tolerancja i szeregi
1 om to mała oporność. W układach elektronicznych stosujemy produkowane masowo i powszechnie dostępne, bardzo tanie rezystory o oporności 0,1 Ω do 22 MΩ (czyli 22000000 Ω), przy czym najczęściej stosujemy rezystory o oporności z zakresu od 100 Ω do 100 kΩ (czyli 100000 Ω).
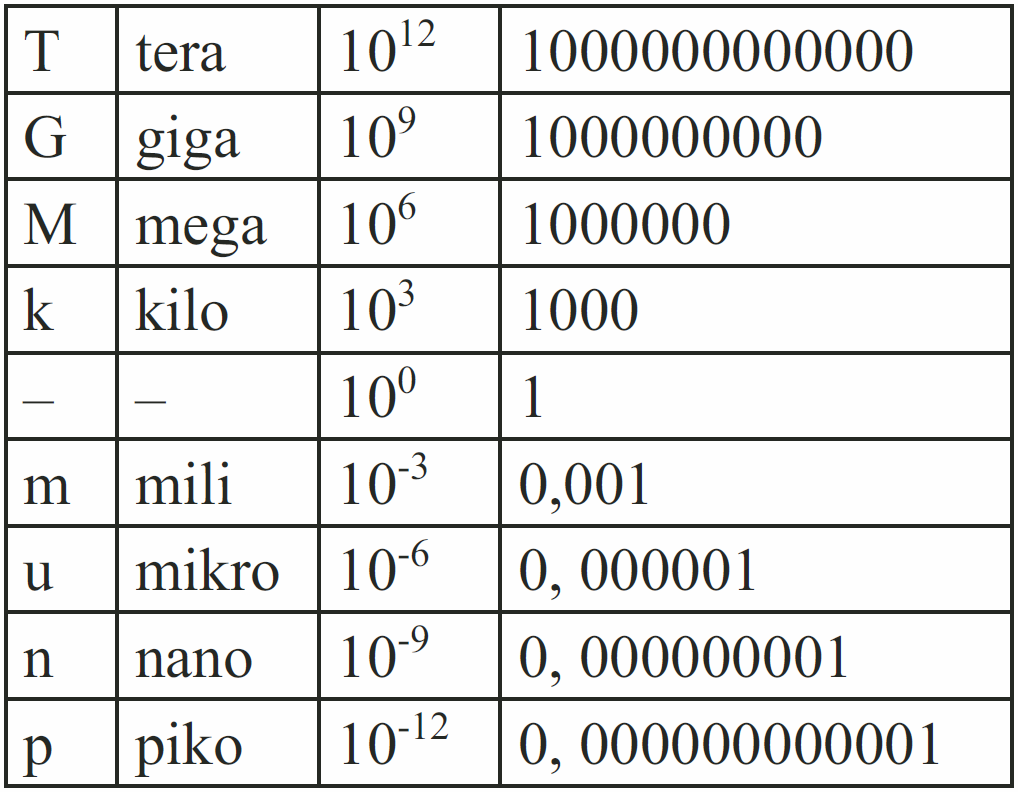
Ponieważ zgodnie z tytułem, cykl przeznaczony jest głównie dla informatyków, muszę wspomnieć, że przedrostki k (kilo), M (mega) i G (giga) mają klasyczne znaczenie. Na przykład kilo to nie 1024, tylko 1000. Dla przypomnienia:
Bardzo rzadko stosuje się rezystory o wartości poniżej 0,1 Ω, czyli 100 miliomów (100 mΩ). Fotografia 12 pokazuje rzadko stosowany rezystor o oporności 0,02 oma, czyli 20 miliomów (20 mΩ). Nie ma rezystorów o wartościach poniżej 1 milioma. Warto wiedzieć, że dłuższa ścieżka na płytce drukowanej ma oporność kilkunastu do kilkudziesięciu miliomów.
Bardzo rzadko można spotkać rezystory o wielkiej oporności, powyżej 22 MΩ. Fotografia 13 pokazuje ciekawostkę: rezystor o wartości 1 GΩ, czyli 1000 MΩ, a niektóre firmy proponują rezystory w wartościach nawet do 100 TΩ (100000000 MΩ).
Należy jednak pamiętać, że warstewka kurzu na płytce drukowanej, zwłaszcza w wilgotnym środowisku, może mieć oporność dużo mniejszą niż 1 GΩ. I właśnie przez ten kurz i zabrudzenia popłyną prądy, tak zwane prądy upływu, większe, niż przez rezystor 1 GΩ. Układy pracujące przy prądach o znikomej wartości, w których miałyby być stosowane rezystory o tak ogromnej oporności rzędu giga-, czy teraomów, muszą mieć odpowiednią konstrukcję i być zabezpieczone przez zabrudzeniem i warunkami atmosferycznymi. Ale to oddzielny, szeroki i dość trudny temat.
My wracamy do spraw podstawowych.
W zdecydowanej większości urządzeń nie jest konieczne stosowanie rezystorów o precyzyjnie dobranej wartości. Często na działanie urządzenia nie ma wpływu zmiana rezystancji nawet o kilkadziesiąt procent. W związku z tym produkuje się rezystory o standardowych wartościach. Dawniej procesy produkcyjne były na tyle niedoskonałe, że trudno było w jednej serii produkcyjnej uzyskać rezystory o dokładnie takiej samej wartości. Poszczególne egzemplarze miały rezystancje różniące się o kilka, a nawet kilkanaście procent. Dlatego dawniej spotykało się też małe rezystory o tolerancji 10%, a nawet 20% – dziś takich rezystorów już się nie produkuje. Popularne małe rezystory mają tolerancję 5%, a ich wartości nominalne są wielokrotnościami tzw. szeregu E24. Szereg E24 obejmuje następujące 24 dobrane równomiernie (w skali logarytmicznej) wartości nominalne:
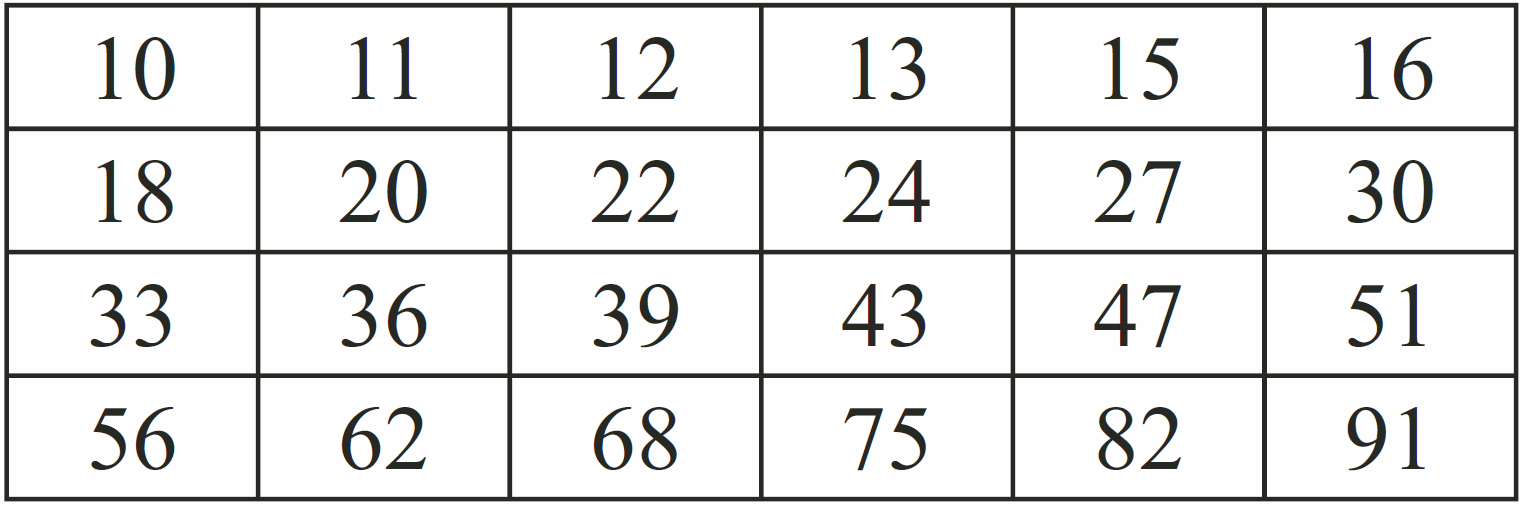
W związku z tym nie znajdziesz rezystora 600 Ω. Popularne rezystory o najbliższych wartościach to 560 Ω i 620 Ω. Nie znaczy to, że rezystor oznaczony 620 Ω ma dokładnie 620,00 Ω. Jego rzeczywista wartość będzie zbliżona do 620 Ω, ale trzeba liczyć się z rozrzutem, zazwyczaj do 5%.
Nie szukaj też rezystora 8,0 kΩ! Wśród popularnych 5-procentowych znajdziesz tylko rezystory 7,5 kΩ i 8,2 kΩ. Produkowane są też tzw. rezystory precyzyjne o tolerancji 2%, 1% oraz 0,5%. Ale i wśród nich nie znajdziesz nominału 8,00 kΩ. Na przykład wśród 1-procentowych najbliższe nominały to 7,87 kΩ oraz 8,06 kΩ. Wartości nominalne rezystorów precyzyjnych są zgodne z szeregami oznaczanymi E48 (2%), E96 (1%) i E192 (0,5%, 0,2% i 0,1%) – o tym później. Wprawdzie u niektórych producentów można zamówić też rezystory o jeszcze węższej tolerancji i dowolnej wartości, jednak hobbysta nigdy takowych nie zamawia – wykorzystuje inne sposoby.
Łączenie szeregowe i równoległe
Elektronik projektujący i budujący układy elektroniczne przeprowadza obliczenia i oczywiście wyniki obliczeń dotyczące wartości stosowanych rezystorów nie dają wartości zgodnych z najpopularniejszym obecnie 5- procentowym szeregiem E24. W przytłaczającej liczbie przypadków nie ma potrzeby stosowania rezystorów precyzyjnych o wąskiej tolerancji, a śmiało można stosować najbliższą wartość z szeregu. Często można zastosować nie tylko najbliższą wartość, ale też następną. Przykładowo, gdy wynik obliczeń da na wyświetlaczu kalkulatora wartość, powiedzmy 19,3674835021, można śmiało zastosować rezystor 18 kΩ lub 20 kΩ, a nawet 22 kΩ.
Przy okazji obliczeń trzeba poruszyć jak najbardziej praktyczne zagadnienie: jaka jest rezystancja zastępcza czy oporność wypadkowa przy łączeniu rezystorów w szereg i równolegle?
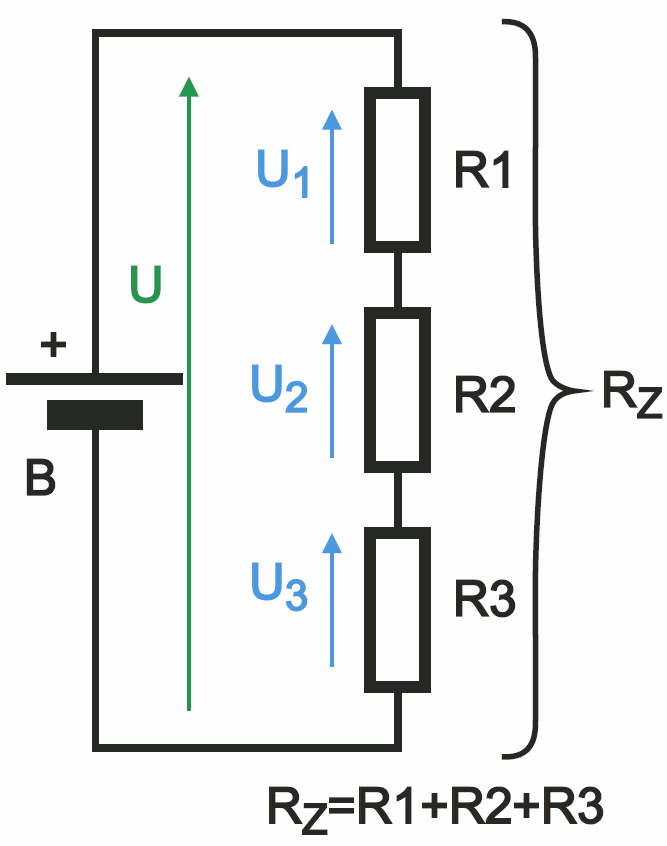
Zgodnie z rysunkiem 14, przy połączeniu szeregowym przez wszystkie rezystory płynie ten sam prąd I, a suma napięć na rezystorach jest równa napięciu źródła. Można więc łatwo wyprowadzić oporność wypadkową (zastępczą) Rz – jest ona równa sumie połączonych szeregowo oporności. Taki wniosek jest też w pełni zgodny z intuicją.
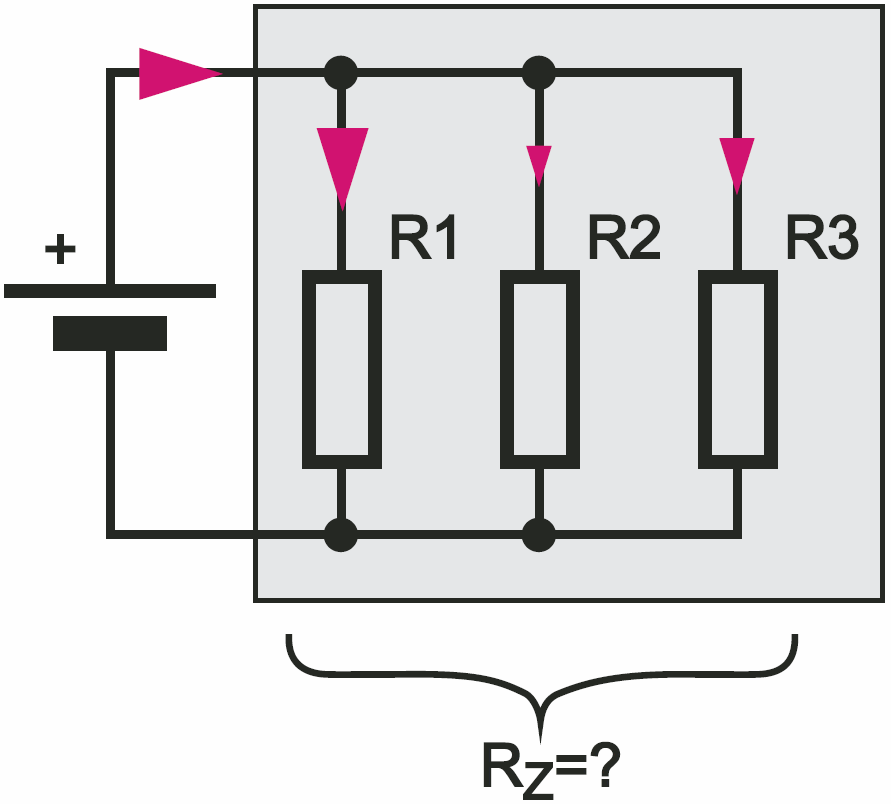
Trudniej jest przy połączeniu równoległym rezystorów – patrz rysunek 15. Na każdym z rezystorów występuje to samo napięcie źródła. Sumują się prądy płynące przez poszczególne rezystory…
Nieprzypadkowo w podręcznikach omawia się pojecie przewodności, która jest odwrotnością rezystancji (analogicznie jak w przypadku oporności, mamy przewodność czynną – konduktancję, przewodność bierną – susceptancję i przewodność zespoloną – admitancję). Pojęcie przewodności czasem ułatwia wykonywanie obliczeń dotyczących równoległego połączenia elementów, ale my nie będziemy się w to wgłębiać. Zapamiętaj natomiast podstawowy wzór dotyczący równoległego połączenia rezystancji:
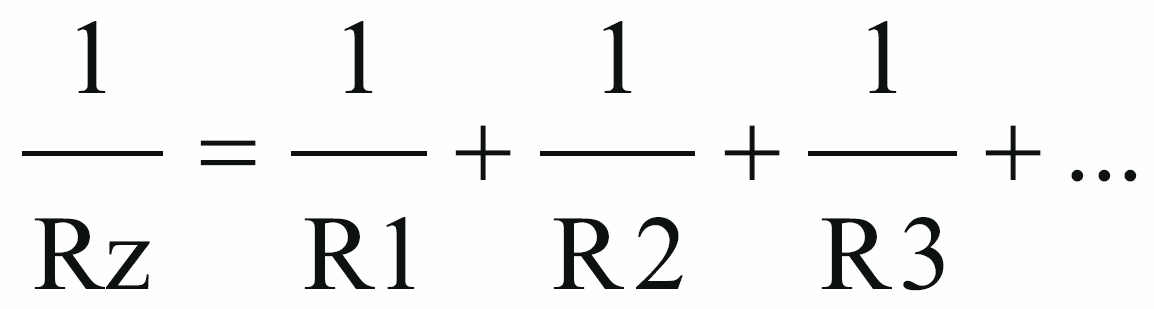
Dla dwóch rezystorów po przekształceniu wzoru 1/Rz = 1/R1 + 1/R2 otrzymujemy:
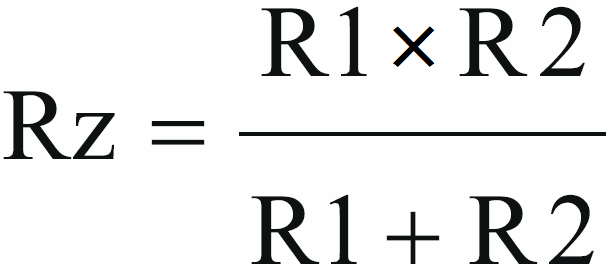
Z tych wzorów często korzystamy. Ale nie zawsze jest to konieczne, bo nie zawsze potrzebna jest precyzja. Zauważ pewne zależności.
Praktyczne obliczenia
Podane dalej wzory i wyliczenia mogą się wydać groźne, trudne i straszne. Nie bój się ich, a w razie potrzeby przeanalizuj ten materiał kilkakrotnie i wykonaj ćwiczenia, ponieważ są to wskazówki jak najbardziej przydatne w praktyce.
Czy już jest dla Ciebie jasne, że rezystancja wypadkowa połączenia równoległego jest mniejsza od najmniejszej z rezystancji składowych?
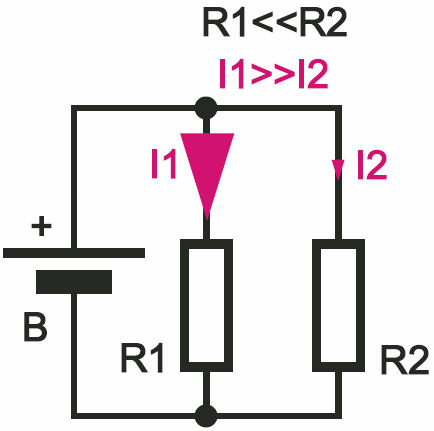
Intuicja słusznie podpowiada, że rezystancja wypadkowa połączenia dwóch jednakowych rezystorów będzie równa połowie rezystancji każdego z nich. Ogólnie N jednakowych rezystorów połączonych równoległe ma rezystancję N razy mniejszą, niż rezystancja każdego z nich. Intuicja podpowiada też, że jeśli do rezystora R1 zostanie dołączony równolegle rezystor R2 o oporności wielokrotnie większej, to wypadkowa rezystancja Rz zmieni się bardzo niewiele, bo dodatkowy prąd płynący I2 będzie wielokrotnie mniejszy od prądu I1. Ilustruje to rysunek 16.
Policzmy rezystancję zastępczą dla wartości X i N-krotnie większej NX:
N=100 Rz = X × 100X / (X +100X) = 0,99X (1%, czyli o ok. 1/100)
N=20 Rz = X × 20X / (X +20X) = 0,952X (4,8% czyli o ok. 1/20)
N=10 Rz = X × 10X / (X +10X) = 0,909X (9,1% czyli o ok. 1/10)
N=5 Rz = X × 5X / (X +5X) = 0,83(3)X (17% czyli o około 1/5)
W nawiasach podałem, o ile procent wypadkowa rezystancja Rz jest mniejsza od rezystancji X. Zauważ, że równoległe dołączenie N-krotnie większej rezystancji zmienia wypadkową rezystancję tylko o około 1/N. Tymczasem w układach stosujemy rezystory 5-procentowe. Jeśli N jest większe niż 20, to często można w ogóle pominąć wpływ tej dołączonej równolegle dużej oporności lub szybko oszacować przybliżoną zmianę oporności według podanej właśnie zależności.
W praktyce dość często musimy obliczyć rezystancję wypadkową równoległego połączenia kilku oporności. Warto do tego wykorzystać jakikolwiek kalkulator z pamięcią i funkcją 1/x. Co bardzo ważne, a o czym zapominają początkujący, wszystkie oporności trzeba podać w tych samych jednostkach: kiloomach, omach czy megaomach. Przykładowo, gdy mamy równolegle połączone rezystory 2,2 kΩ, 1,1 kΩ i 820 Ω, musimy obliczyć Rz ze wzoru:
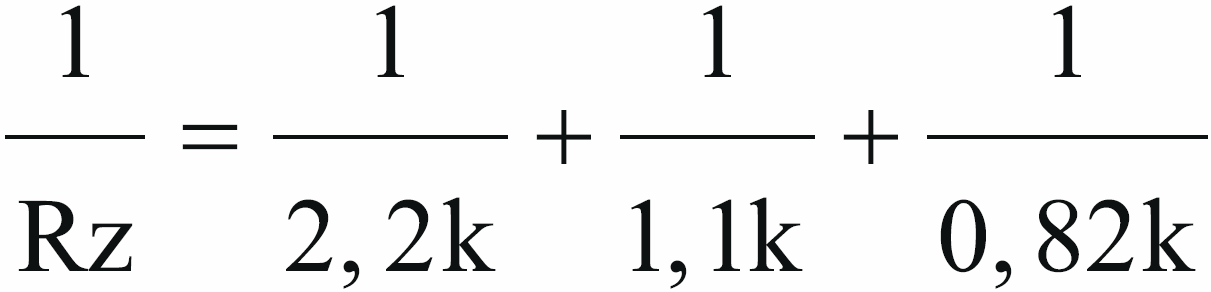
W tym celu w kalkulatorze kolejno zrealizujemy:
2,2 – wartość pierwszej rezystancji
1/x – obliczamy odwrotność
M+ – wpisujemy wynik do pamięci
1,1 – wpisujemy wartość drugiej rezystancji
1/x – obliczamy odwrotność
M+ – dodajemy wynik do pamięci
0,82 – wartość trzeciej rezystancji w kiloomach
1/x – obliczamy odwrotność
M+ – dodajemy wynik do pamięci
MR – odczytujemy wynik z pamięci
1/x – obliczamy i odczytujemy wartość Rz
Wykonaj te obliczenia i sprawdź, czy wynik jest równy 0,38712446. Gdyby trzeba było taką rezystancję zrealizować, zastosujemy 5- procentowy rezystor 390 Ω.
W praktyce często musimy przeprowadzić pokrewne obliczenia: do rezystora R1 o znanej wartości chcemy dołączyć rezystor o takiej wartości Rx, żeby otrzymać rezystancję wypadkową równą Rz. Przekształcamy wzór 1/Rz = 1/R1 + 1/Rx:
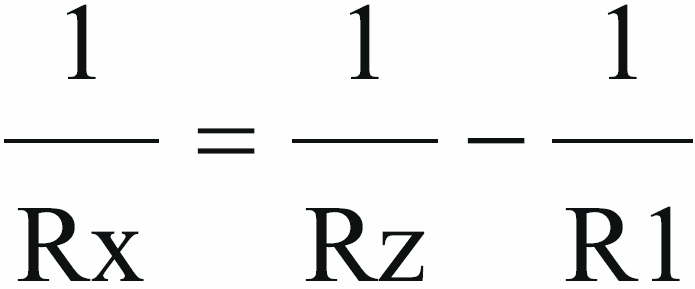
Zamiast tego wzoru i nieco zmodyfikowanej procedury z kalkulatorem możemy też wykorzystać przekształcony wzór:
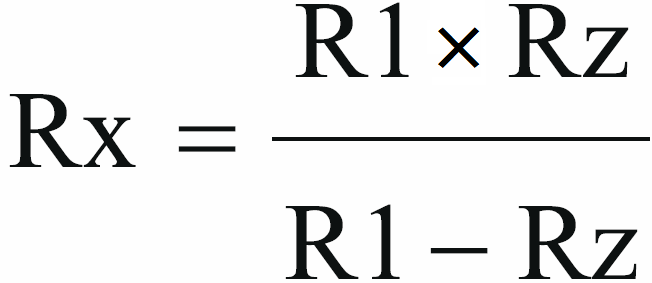
Oto przykład. W układzie powinniśmy zastosować rezystor o wartości 750 Ω. Nie mamy takiego. Z posiadanych rezystorów o mniejszej wartości też nie złożymy w szereg potrzebnej wartości. Mamy natomiast rezystory 910 Ω i 1 kΩ i chcemy zastosować rozwiązanie według rysunku 17.
Za pomocą kalkulatora, dla pierwszego przypadku (R1=910 Ω) obliczymy Rx = 4,265 kΩ. Dla drugiego (R1=1 kΩ), Rx = 3 kΩ. Zastosujemy 910Ω i posiadany rezystor o nominale 4,3 kΩ, bo nie mamy potrzebnego 3,0 kΩ. Wprawdzie teoretycznie równoległe połączenie 0,91 kΩ i 4,3 kΩ nie daje idealnie 750 Ω, tylko 751 Ω, ale to oczywiście nie ma to znaczenia z uwagi na tolerancje.
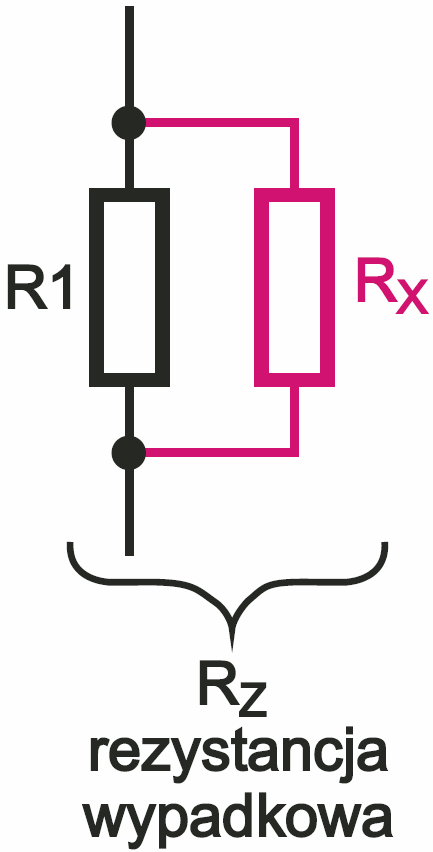
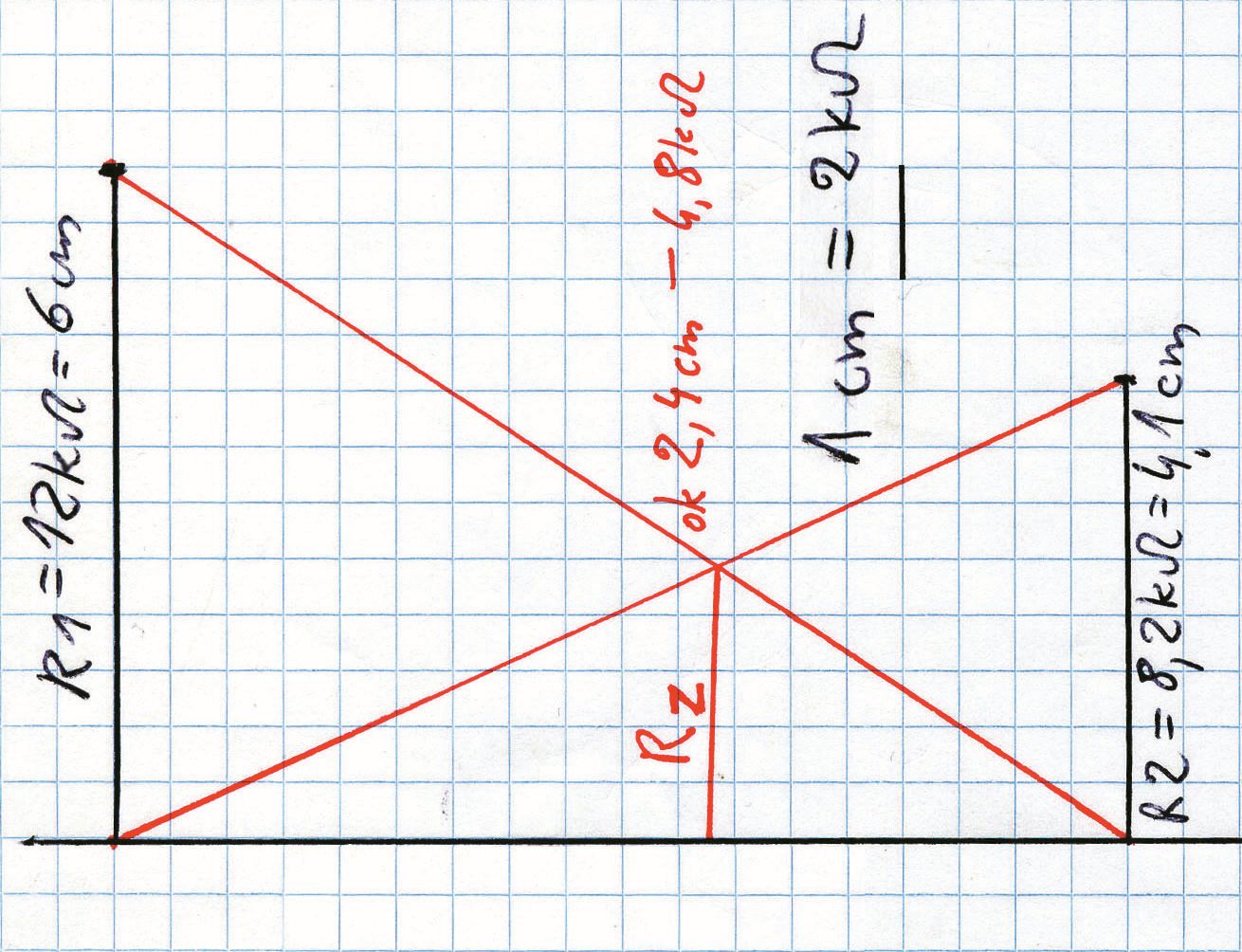
I jeszcze jeden sposób obliczeń: W przypadku połączenia równoległego dwóch oporników, zamiast obliczeń można wykorzystać prostą metodę geometryczną. Wystarczy kawałek kartki w kratkę, linijka i długopis. Na poziomej „podstawie” w dowolnej odległości od siebie, „stawiamy” dwa odcinki o długościach odpowiadających obu rezystancjom. Rysujemy „przekątne” i odległość punktu przecięcia od poziomej „podstawy” określa wypadkową rezystancję. Rysunek 18 pokazuje przykład obliczania wypadkowej rezystancji Rz, gdy R1=12 kΩ, R2=8,2 kΩ. Wynik „graficzny” zależy od dokładności rysunku. Tę samą zasadę można też wykorzystać do znalezienia potrzebnej wartości Rx, by z R1 uzyskać daną wartość Rz.
Obciążalność
Zgodnie z informacjami w poprzedniego wykładu, występowanie napięcia i przepływ prądu związane jest z mocą. W przypadku rezystorów cała moc elektryczna zamienia się na ciepło. I to ze 100-procentową sprawnością. Ilość ciepła wydzielonego w rezystancji określona jest nie tylko podstawowym, wzorem:
![]()
ale też wygodnymi w praktyce wzorami pochodnymi:
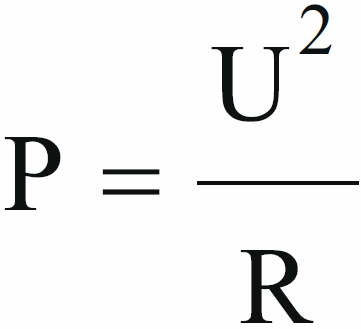
![]()
Zapamiętaj wszystkie trzy – na pewno będziesz z nich korzystał.
Przykładowo jeśli przez rezystor płynie prąd 500 mA i występuje na nim napięcie 9 V, to wydziela się w nim 4500 mW, czyli 4,5 W mocy w postaci ciepła.
Jak już wiesz, w sumie problemem jest wzrost temperatury, ponieważ zawsze całe wytworzone w rezystorze ciepło trzeba na bieżąco rozproszyć do otoczenia. Już intuicja podpowiada, że czym większe rozmiary ma rezystor, tym większą ma obciążalność, czyli może się w nim wydzielić więcej mocy (ciepła strat). Zasadniczo w przypadku rezystorów nie obowiązuje zasada, że temperatura nie może przekroczyć +150°C – to ograniczenie dotyczy większości półprzewodników krzemowych. Moc, a ściślej obciążalność rezystorów zależy od szczegółów konstrukcji oraz użytego materiału czynnego.
Na przykład duży rezystor MŁT (czerwony na fotografii 19) ma obciążalność tylko 2 W.
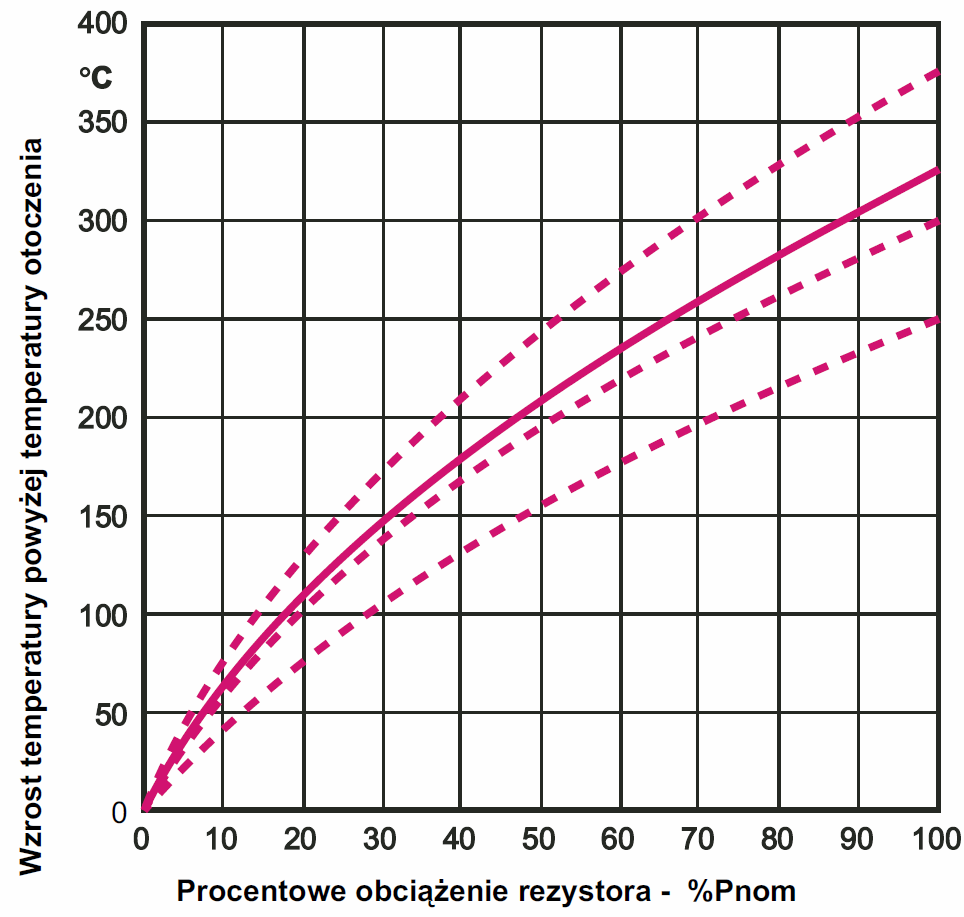
Natomiast rezystory drutowe mogą osiągać temperaturę nawet do +350°C, dlatego ten zielony pokazany na fotografii 19, ma obciążalność 8 W przy takich samych rozmiarach. W rezystorze MŁT cienka metalowa warstwa czynna i lakierowe pokrycie nie mogą prawidłowo pracować w aż tak wysokich temperaturach. Natomiast drut oporowy i ceramika zielonego rezystora typu RDCO mogą pracować w podanej wysokiej temperaturze. Rysunek 20 pokazuje, na ile temperatura podobnych rezystorów drutowych wzrasta powyżej temperatury otoczenia w zależności od obciążenia w zakresie 0…100% mocy nominalnej. Linie przerywane dotyczą rozmaitych warunków pracy (chłodzenia).
Warto zauważyć, że temperatura topnienia klasycznego stopu lutowniczego (cyny) wynosi około 183°C. Oznacza to, że w pełni obciążony rezystor RDCO może się… sam wylutować podczas pracy urządzenia. I takie przypadki się zdarzają w źle zaprojektowanych płytkach, gdzie rezystor taki jest montowany na krótkich wyprowadzeniach, tuż nad płytką. Przed wielu laty takie przypadki zdarzały się nawet w sprzęcie fabrycznym – w źle zaprojektowanych modułach telewizorów. Jeśli chodzi o rezystory małej mocy, to ich obciążalność też nie jest wprost proporcjonalna do ich rozmiarów. Szczegółów należałoby szukać w katalogach, ale nie zawsze jest to możliwe, bo podobnie wyglądające elementy pochodzące od różnych wytwórców mogą mieć znacząco różną obciążalność. W przypadku najpopularniejszych współczesnych rezystorów, pokazanych na fotografii 21 można bezpiecznie przyjąć, że mają one obciążalność 0,25 W.
Warto wiedzieć, że nie jest to ścisła granica. Krótkotrwałe przeciążenie, nawet do 1 W nie zniszczy takiego rezystora. Stanie się on bardzo gorący i rozgrzeje się na nim lakier, ale do uszkodzenia nie dojdzie. Fotografia 21 pokazuje też, jak wyglądają popularne rezystory 100 Ω 5% 0,25 W po przeciążeniu. Podłączenie rezystora 100 Ω do napięcia 22,36 V spowoduje przepływ prądu 223,6 mA i wydzielenie w rezystorze mocy 5 W. Górny rezystor obciążony mocą 5 W po niecałych dziesięciu sekundach zapalił się żywym płomieniem. Środkowy rezystor, podłączony do napięcia 14,1 V, czyli przy obciążeniu 2 W po około pół minucie zaczął lekko dymić i zmieniać kolor. O towarzyszących temu zapachach nie wspomnę. Natomiast dolny rezystor, podłączony do napięcia 10 V, czyli obciążony mocą 1 W był gorący, ale kilka minut takiej pracy nie spowodowało żadnych widocznych uszkodzeń.
Rysunek 20 dotyczy rezystorów drutowych większej mocy, natomiast temperatura popularnych rezystorów węglowych i metalizowanych wzrasta znacznie mniej. Można przyjąć, że temperatura małych rezystorów o obciążalności 0,25 W, obciążonych taką mocą nominalną wzrośnie o około 25…40°C.
Na marginesie warto też wspomnieć o postępie i o maleńkich rezystorach do montażu powierzchniowego – fotografia 22. Nigdy nie wpadnij na pomysł, że są to „lepsze rezystory”, mające „mniejsze straty”.
Niech Ci nie przyjdzie do głowy, że w starych wydzielało się dużo ciepła, a w nowoczesnych, miniaturowych – dużo mniej, bo są nowocześniejsze. W żadnym wypadku! W tej kwestii nie ma i nie może być żadnego postępu. Rezystory miały i mają sprawność 100%, więc cała moc P=U×I wydziela się w postaci ciepła. Owszem, postęp jest, ale polega na przykład na tym, że element może pracować w wyższej temperaturze. Rzeczywiście niektóre maleńkie rezystory SMD mają zaskakująco dużą obciążalność, ale tylko przy dobrych warunkach odprowadzania ciepła (np. zamontowane na płytkach ceramicznych).
Napięcie maksymalne i prąd maksymalny
Zasadniczo maksymalne napięcie i maksymalny prąd wynikają z podanej w katalogu obciążalności rezystora. Przy maksymalnym napięciu i maksymalnym prądzie wydzielająca się w rezystorze moc strat będzie równa obciążalności. Dlatego trzeba korzystać ze wzorów:
![]()
gdzie P to obciążalność rezystora, R – jego rezystancja.
Zapamiętaj, że tak obliczone napięcie maksymalne Umax w angielskojęzycznych katalogach oznaczane jest RCWV = Rated Continuous Working Voltage.
Przykładowo dla małego rezystora 1 kΩ 0,25 W:
Umax = RCWV = 15,8 V Imax = 15,8 mA
Natomiast dla rezystora 47 kΩ 0,25 W:
Umax = RCWV = 108 V Imax = 2,3 mA
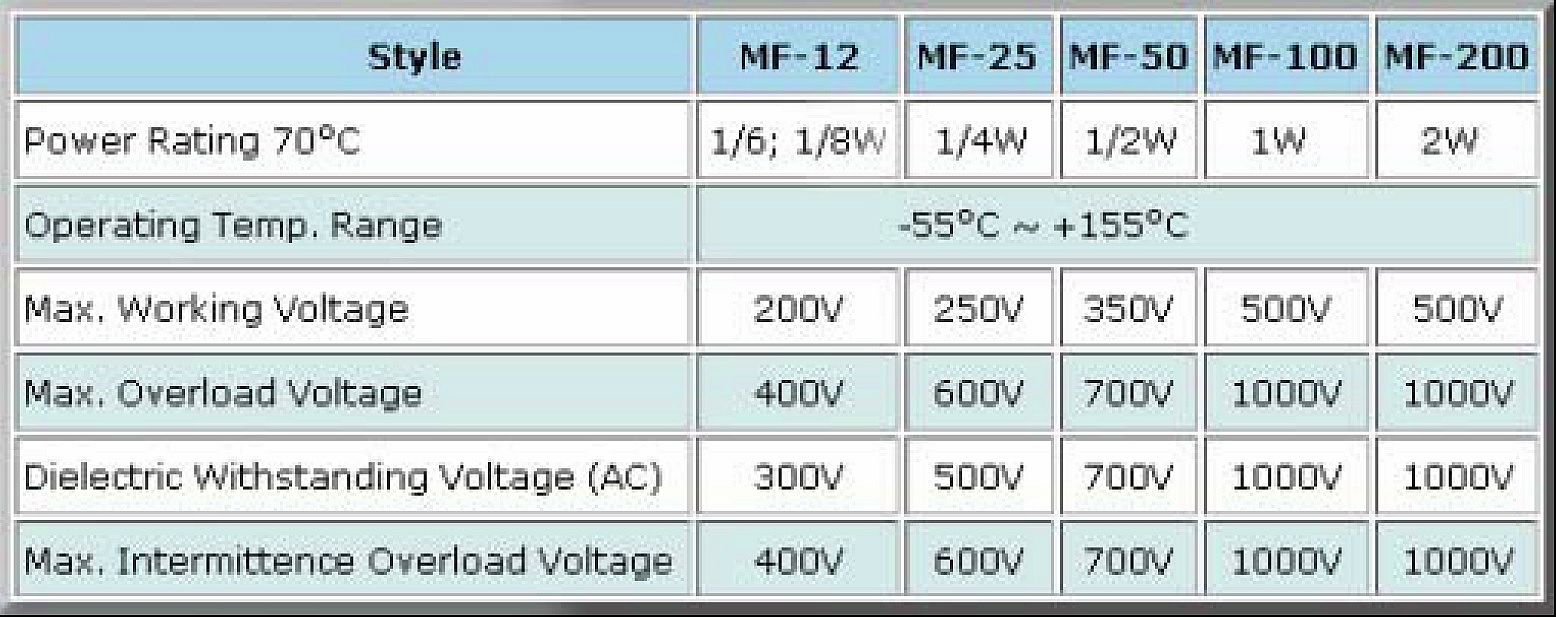
Łatwo też sprawdzić, że na przykład dla 0,5- watowego rezystora o rezystancji 10 MΩ tak obliczone napięcie maksymalne wynosiłoby aż 2236V, czyli sporo ponad 2 kilowolty. Już na oko widać, że to za dużo i coś tu nie gra. Wprawdzie obliczenia dotyczące mocy są prawidłowe, ale w grę wchodzi dodatkowo wytrzymałość napięciowa izolacji i sprawa przebicia między zwojami spirali rezystora. Popularne rezystory mają zwykle napięcie maksymalne 200…500 V, zależnie od rozmiarów. W katalogach zazwyczaj podane jest kilka wartości napięcia maksymalnego: Max. Working Voltage, Max. Overload Voltage, Dielectric Withstanding Voltage (AC), Max. Intermittence Overload Voltage. Rysunek 23 pokazuje pochodzący z Internetu przykład dotyczący rezystorów węglowych różnej mocy i wielkości pewnego producenta z Azji.
Hobbysta nie musi wgłębiać się w szczegóły. Może ostrożnie przyjąć, że małe popularne rezystory mają napięcie maksymalne 200 V i jeśli napięcie na rezystorze miałoby być większe, należy dwa jednakowe rezystory połączyć w szereg.
A w kolejnym odcinku zajmiemy się rezystorami precyzyjnymi.
Piotr Górecki