Elektronika (nie tylko) dla informatyków (25) Filtrowanie i powielanie

W poprzednim odcinku doszliśmy do wniosku, że na równoległym obwodzie rezonansowym mogłoby wystąpić bardzo duże napięcie, jeżeli byłby on zasilany ze źródła prądowego, a konkretnie z obwodu kolektora lub drenu tranzystora. Wspomniałem wtedy, że ograniczeniem jest tranzystor. Przyjrzyjmy się temu bliżej.

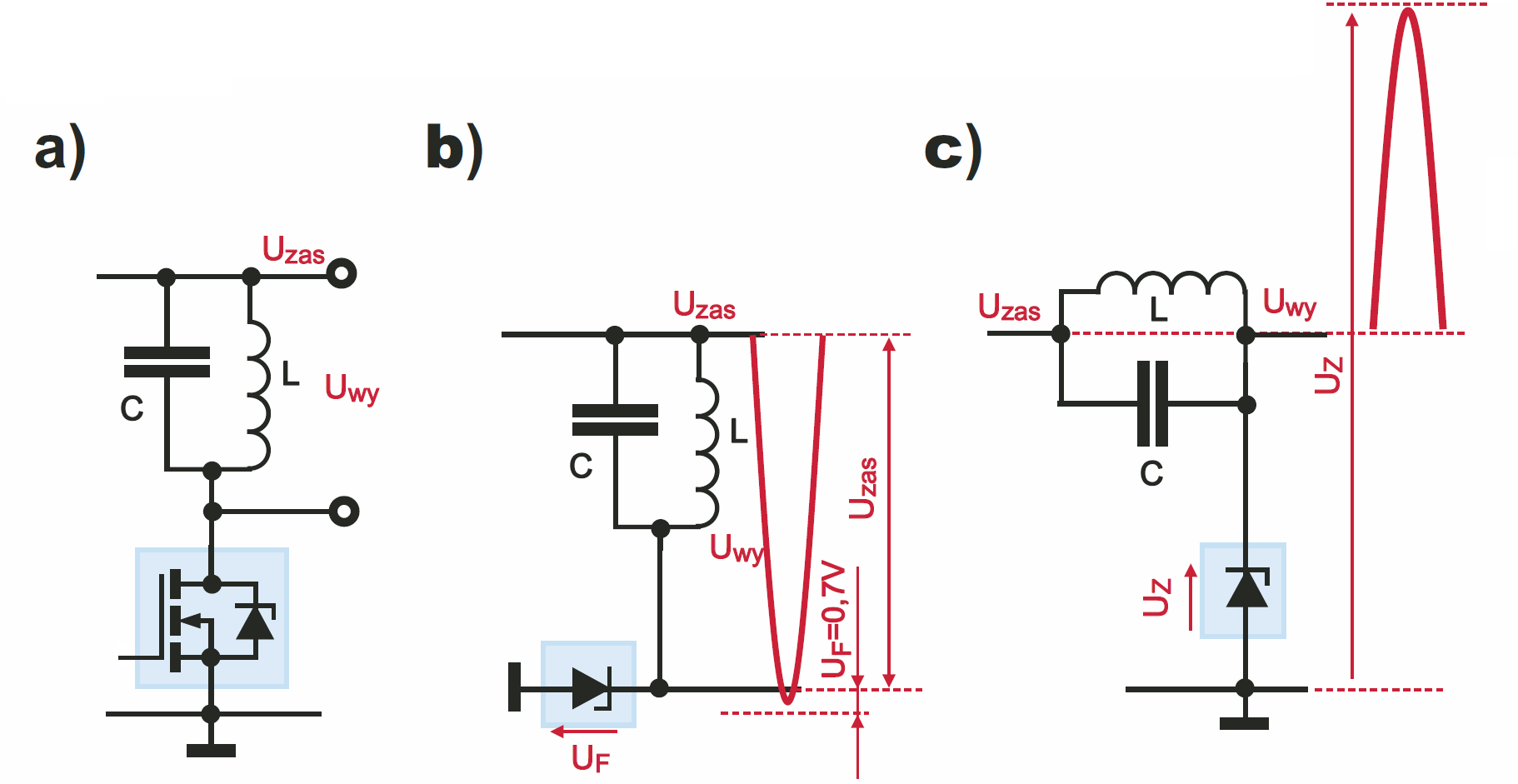
Otóż szczególnie łatwo zrozumieć problem w przypadku tranzystora MOSFET, który jak wiadomo, zawiera pasożytnicze struktury, zachowujące się jak dioda, a nawet jak dioda Zenera o napięciu nieco wyższym od jego katalogowego napięcia U_DS (rysunek 1a). W układzie z MOSFET-em N obecność takiej „diody” uniemożliwi przede wszystkim obniżenie się napięcia o więcej niż 0,7 V poniżej masy, jak pokazuje rysunek 2b. Mniejszym problemem jest dodatnia połówka i przepływ prądu przez „diodę Zenera” według rysunku 3c, ponieważ zawsze można zastosować tranzystor o wyższym napięciu U_DS, gdzie „napięcie Zenera U_Z” będzie większe.

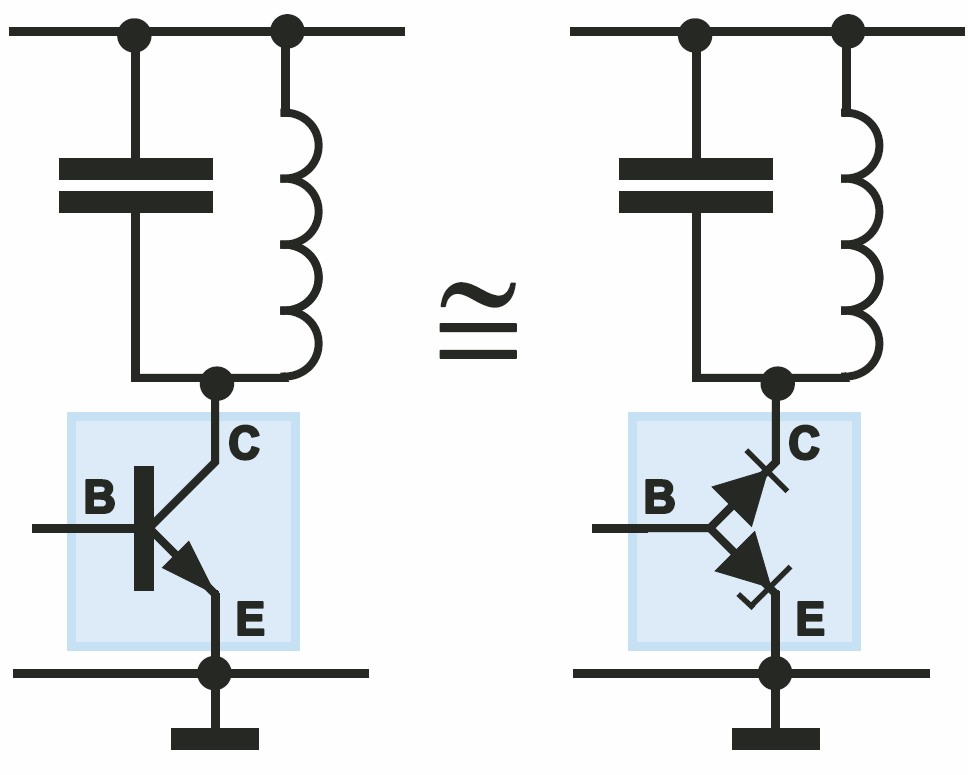
W tranzystorze bipolarnym jest podobny problem, ponieważ złącze kolektor-baza jest złączem PN (a ponadto złącze baza-emiter zachowuje się jak dioda Zenera o napięciu około 6…7 V), jak ilustruje rysunek 2.

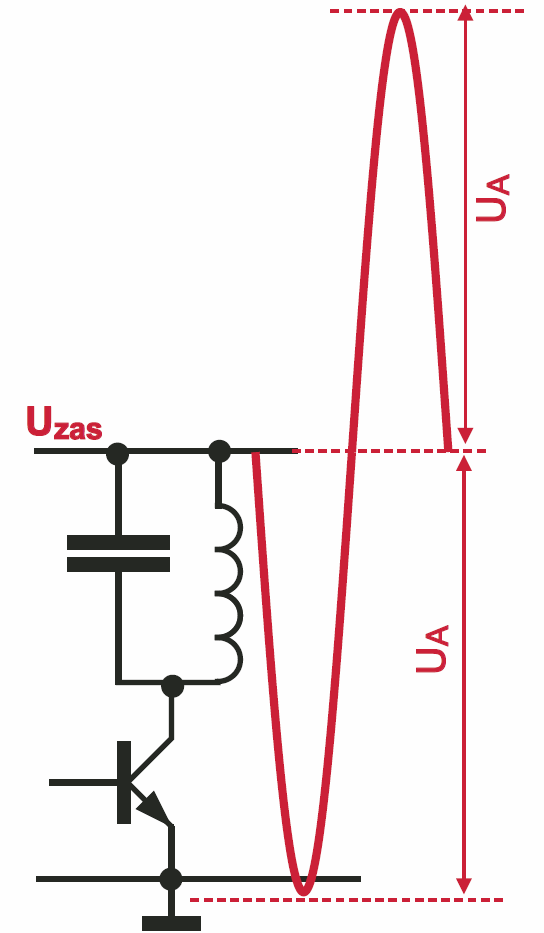
W każdym razie obecność tranzystora, czy to bipolarnego NPN, czy MOSFET-a N, nie pozwoli, by napięcie wytworzone w cewce obniżyło się znacząco poniżej masy. Wprawdzie napięcie to mogłoby „rosnąć w górę” bez ograniczeń, ale na cewce występuje sygnał przemienny, a to oznacza, że także część dodatnia, przewyższająca dodatnie napięcie zasilania, będzie mieć amplitudę taką, jak część ujemna – patrz rysunek 3.

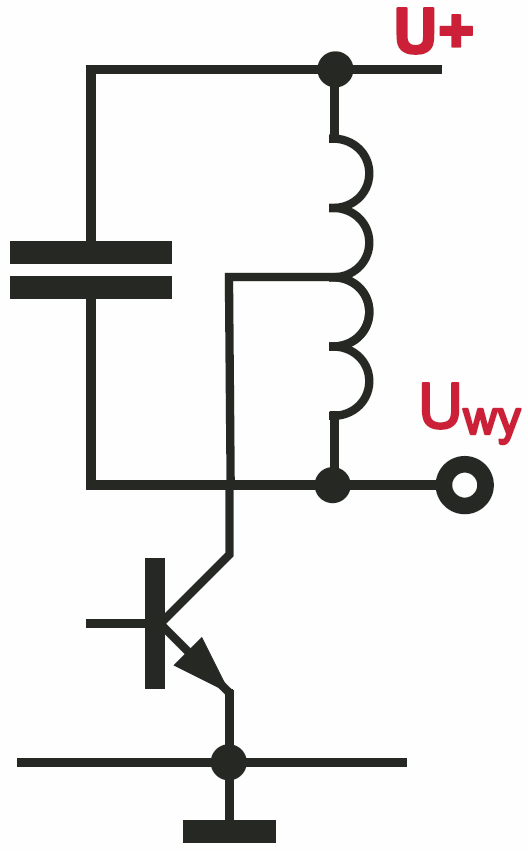
Podobnie jest z tranzystorami PNP i MOSFET P: w praktyce nie uda się w zwykłym obwodzie LC uzyskać napięcia wyjściowego o wartości międzyszczytowej znacząco większej niż podwójna wartość napięcia zasilania. Większe wartości można łatwo uzyskać, stosując cewkę z odczepem według rysunku 4, ale to już inna historia.

Filtrowanie

A teraz kolejna ważna sprawa. Mówiliśmy, że rezonans to zjawisko związane z wymuszeniem przez zewnętrzne źródło napięciowe lub prądowe. Wiadomo też, że obwody rezonansowe pełnią rolę filtrów, bo „lubią swoją częstotliwość rezonansową”. I wszystko jest jasne, jeśli przebieg wymuszający jest sinusoidą.

Obwód rezonansowy przepuszcza składniki o częstotliwościach bliskich f₀, a tłumi inne. Od stu lat wykorzystujemy to w odbiornikach radiowych, by spośród mnóstwa sygnałów wyłowić ten jeden, o częstotliwości naszej ulubionej stacji.

Ale spójrzmy na to nieco inaczej: przecież w praktyce zazwyczaj mamy do czynienia z przebiegami o innych kształtach niż sinusoida. I właśnie wtedy obwód rezonansowy LC ma pełnić rolę filtru. Jak zachowa się obwód rezonansowy, gdy wymuszenie nie jest sinusoidą?

Wbrew pozorom odpowiedź jest prosta, o ile tylko pamiętasz, że sinusoida jest „elementarnym” przebiegiem i że przebieg o dowolnym kształcie jest w istocie złożeniem sygnałów sinusoidalnych o częstotliwościach harmonicznych. Ilustruje to rysunek 5, gdzie kolorem zielonym zaznaczony jest przebieg wymuszający, podobny trochę do prostokątnego, natomiast kolorem czerwonym zaznaczone są jego sinusoidalne składniki. Chodzi o tzw. rozkład Fouriera i zagadnienia, które już przerobiliśmy przy omawianiu właściwości kondensatorów. Jeśli masz wątpliwości, wróć do tego materiału w tym wykładzie.

Zgodnie z rysunkiem 5, pobudzanie obwodu rezonansowego przebiegiem odkształconym należy rozumieć jako pobudzanie go jednocześnie wszystkimi składowymi sinusoidami. Oczywiście jak wskazują rysunki 2 i 7 w tym odcinku, obwód ten będzie reagował głównie na składniki o częstotliwościach bliskich częstotliwości rezonansowej f₀. Te składniki przepuści, a pozostałe silnie stłumi. W efekcie na wyjściu pojawią się wszystkie te składniki wejściowe, ale stłumione w różnym stopniu, niektóre bardzo silnie.

Właśnie obwody rezonansowe o dużej dobroci, pracujące w roli filtrów, pozwalają udowodnić prawdziwość twierdzenia Fouriera. Ale nie wpadnij przypadkiem na pomysł, że obwód rezonansowy może zmienić częstotliwość przebiegu, żeby „podciągnąć ją bliżej częstotliwości f₀”. Nie, zmiana częstotliwości nie jest możliwa. Obwód rezonansowy po prostu w różnym stopniu stłumi poszczególne składowe (harmoniczne) sygnału wejściowego. Przyjrzyjmy się temu nieco bliżej.

Przebieg z rysunku 5 ma częstotliwość zbliżoną do częstotliwości f₀ obwodu rezonansowego, na który zostanie podany. Wtedy wyższe harmoniczne zostaną stłumione i przebieg wyjściowy będzie przypominał sinusoidę o częstotliwości bliskiej f₀, ale nieco zniekształconą przez obecność nie do końca stłumionych składników o innych częstotliwościach. Nic więc dziwnego, że obwody rezonansowe często służą do zamiany przebiegu prostokątnego, lub nawet krótkich impulsów, na przebieg sinusoidalny. Może to być prosty układ, jak na rysunku 3b w poprzednim odcinku, z obwodem rezonansowym o częstotliwości f₀, równej częstotliwości sygnału wejściowego. Po prostu obwód LC tłumi wyższe harmoniczne. Oczywiście czym większa dobroć Q, tym skuteczniejsze to czyszczenie i sygnał wyjściowy jest czystszą sinusoidą.

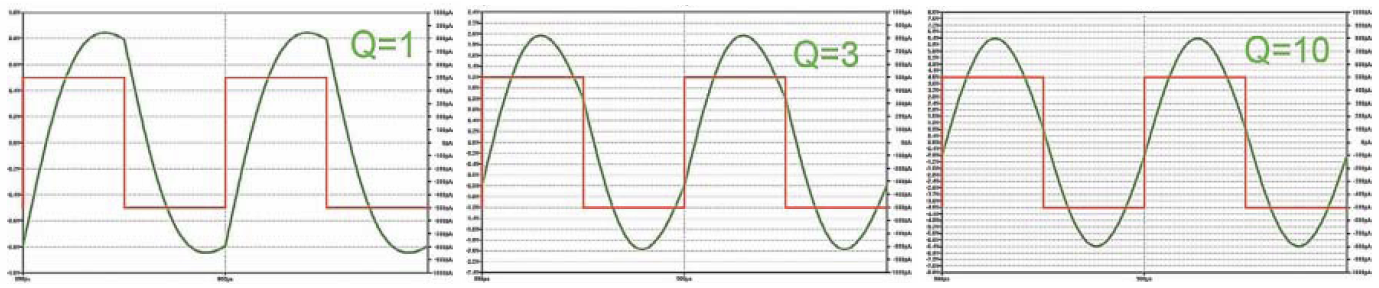
Rysunek 6 ilustruje skuteczność „czyszczenia” przebiegu prostokątnego o częstotliwości f₀, w zależności od wypadkowej dobroci obwodu RLC. Zielone przebiegi pokazują napięcie na obwodzie rezonansowym o bardzo kiepskiej dobroci Q = 1. Widać wyraźnie, że przebieg jest odkształcony i daleko mu do sinusoidy. Przy dobroci Q = 3 jest znacznie lepiej, ale też jeszcze widać zniekształcenia sinusoidy w chwilach, gdy w czyszczonym przebiegu prostokątnym występują zbocza. Przy dobroci Q = 10 takich zniekształceń już prawie nie widać. Jednak dopiero przy jeszcze większej dobroci przebieg wyjściowy byłby sinusoidą o znikomych zniekształceniach.

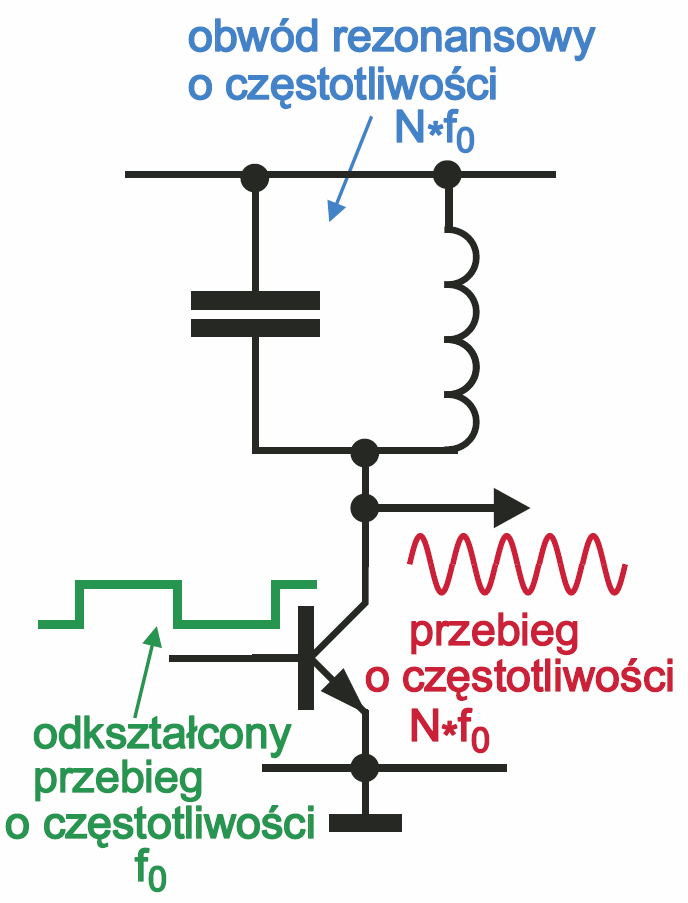
Ale nie zawsze częstotliwość odkształconego przebiegu wejściowego jest zbliżona do częstotliwości f₀. Jeśli byłaby dużo większa, to wszystkie jego składowe harmoniczne będą odległe od częstotliwości rezonansowej i obwód LC wszystkie silnie stłumi – praktycznie nie zareaguje na taki sygnał. Inaczej będzie, jeśli odkształcony przebieg będzie miał częstotliwość mniejszą od f₀. Wtedy wszystko zależy od zawartości harmonicznych. Jeśli tylko ten odkształcony przebieg będzie zawierał harmoniczne o częstotliwościach bliskich f₀, to zostaną one przepuszczone, a pozostałe, łącznie z podstawową – stłumione. Na wyjściu pojawi się przebieg o częstotliwości będącej wielokrotnością częstotliwości przebiegu wejściowego. Nie jest to wcale teoretyczny eksperyment myślowy. Od lat tego rodzaju układy, zwane powielaczami częstotliwości, są wykorzystywane w praktyce. Mogą być na przykład realizowane w prosty sposób, choćby z wykorzystaniem tranzystora według rysunku 7.

Przebieg wejściowy ma częstotliwość f₀, ale jest zniekształcony, więc zależnie od rodzaju zniekształceń, zawiera w różnych proporcjach także składowe (harmoniczne) o częstotliwościach 2×f₀, 3×f₀, 4×f₀, 5×f₀, 6×f₀,… ,a przynajmniej harmoniczne nieparzyste. Obwód LC ma częstotliwość rezonansową N×f₀, przy czym zazwyczaj wykorzystuje się nieparzyste harmoniczne. Po prostu obwód rezonansowy przepuszcza konkretną harmoniczną o „swojej” częstotliwości, a pozostałe tłumi. Idea jest bardzo prosta, ale czym wyższa harmoniczna, tym jej zawartość w odkształconym przebiegu jest mniejsza, dlatego w ten sposób uzyskuje się częstotliwości 3f₀, 5f₀, rzadko 7f₀. W sumie takie powielanie okazuje się znacznie trudniejsze od zwykłego „czyszczenia” z rysunku 6.

Rysunek 8 ilustruje problem uzyskania, a ściślej odfiltrowania harmonicznej o częstotliwości 7f₀. Z przebiegu prostokątnego o częstotliwości f=10 kHz chcemy wyłowić tylko siódmą harmoniczną (70 kHz) za pomocą obwodu LC nastrojonego właśnie na te 70 kHz Przy bardzo dużej dobroci obwodu LC nie byłoby żadnego problemu i na wyjściu uzyskalibyśmy piękną sinusoidę 70 kHz – w prawej części rysunku 8 pokazany jest prostokątny przebieg wejściowy o częstotliwości 10 kHz i „wyciągnięty z niego” sinusoidalny przebieg w obwodzie rezonansowym 70 kHz o dobroci Q = 1000. Ale jeśli dobroć obwodu rezonansowego byłaby mniejsza, to najbliższe niepożądane harmoniczne nie będą dostatecznie tłumione i przebieg wyjściowy nie będzie już czystą, regularną sinusoidą o częstotliwości 70 kHz, jak pokazują pozostałe przebiegi na rysunku 8.

Podane tu informacje tylko w ogólnym zarysie przedstawiają możliwości i problemy związane z wykorzystaniem obwodów rezonansowych w roli filtrów. Jednak obecnie filtry realizuje się w inny sposób albo za pomocą wzmacniaczy operacyjnych, albo metodami cyfrowymi, dlatego nie będziemy zagłębiać się w problematykę filtrów LC. A w następnym odcinku oraz w kolejnych odcinkach cyklu zajmiemy się transformatorami.

Piotr Górecki