„Wiatr” Poyntinga – uzupełnienie

W artykule „Wiatr Poyntinga i okoliczności przewodowe” w ZE 2/2025, Piotr Górecki przedstawił sporo argumentów aby przekonać, że energia wcale nie przepływa w przewodach, tylko w szerokim otoczeniu przewodów – prowadnic, że przepływa w postaci czegoś nazwanego tam „wiatrem Poyntinga”.

Trudno powiedzieć, ilu Czytelników wspomniane powyżej opracowanie zdoła przekonać, a ilu pozostanie sceptycznych. Dodatek, czyli uzupełnienie, które chcę przedstawić w tym krótkim opracowaniu powinno zwiększyć „współczynnik przekonanych”.

Prawdą jest, że trudno jest doliczyć się, czy „wiatr Poyntinga” przewieje tyle energii ile należy. Sytuacja jest w miarę prosta w kablu koncentrycznym, który jednoznacznie ogranicza przestrzeń w której zamyka się pole elektryczne i magnetyczne, czyli elektromagnetyczne. W ogólnym przypadku trzeba by całkować po całej przestrzeni, aby przekonać się czy wszystko się zgadza. W ogólnym przypadku jest to dość skomplikowane matematycznie. Jednak w sytuacji najprostszej geometrii, zadanie to upraszcza się znakomicie.

Rezystor

Załóżmy, że mamy rezystor wykonany z drutu oporowego o przekroju kołowym o średnicy 2r i długości L. Czyli mamy walec o przekroju πr² i o długości L. Materiał z którego wykonany jest ten opornik ma jakąś rezystancję właściwą ρ (ro). Chcemy się przekonać, czy wektor Poyntinga wnikający do tego rezystora przez jego powierzchnię zewnętrzną przeniesie tyle energii, ile należy oczekiwać z prawa Joule’a.

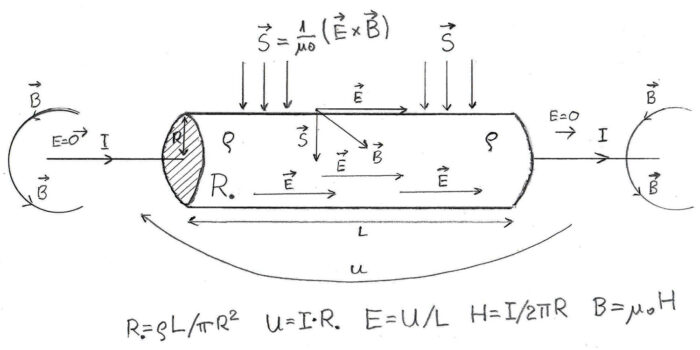
Sytuację, którą będziemy rozważać pokazuje rysunek 1. Moc wydzielana w rezystorze (i zamieniana na ciepło), to oczywiście iloczyn napięcia na nim przemnożonego przez prąd. Czyli, szkolny wzór P=U×I. Zobaczmy, jak to wygląda od strony „Poyntinga”. Dla uproszczenia przyjmiemy, że długość L rezystora jest dużo większa od jego średnicy. Pozwoli to uprościć rachunki przyjmując, że powierzchnia zewnętrzna rezystora równa jest 2πr×L.

Mamy tu do czynienia z prądem stałym, a prosta geometria naszego opornika pozwala wywnioskować, że pole elektryczne w jego objętości jest jednorodne. Pole E łatwo wyliczyć jako stosunek napięcia U na końcach tego rezystora, podzielone przez jego długość L. A więc E=U/L. E jest oczywiście wektorem, a więc musimy jeszcze dopowiedzieć jaki ma kierunek. Z symetrii geometrycznej naszego rezystora – walca nietrudno stwierdzić, że wektor E jest równoległy do osi walca w całej objętości naszego opornika.

Ustaliliśmy jak wygląda natężenie pola elektrycznego, a co z wektorem B lub H? Z prawa Ampera wynika jednoznacznie, iż rotacja H jest równa wprost gęstości prądu w danym punkcie. Łatwiej będzie posłużyć się całkową postacią tego prawa, czyli powiedzieć, iż wektor H przemnożony przez kontur otaczający nasz opornik, równy jest całkowitemu prądowi jaki przez ten kontur przepływa. Weźmy kontur przy powierzchni naszego walca – opornika. Należy więc napisać: 2πr×H=I. H to oczywiście też wektor, a jego kierunek również określimy z symetrii i geometrii naszego rezystora. Wektor H jest styczny do powierzchni naszego opornika, i położony jest na okręgu koła będącego przekrojem poprzecznym tego rezystora. Wektory E i H są względem siebie prostopadłe, a więc nie będzie kłopotu z policzeniem iloczynu wektorowego. Sinus kąta prostego jest równy jeden, a więc wektor Poyntinga jest równy iloczynowi S=E×H=U/L×I/2πr. Wektor S to strumień energii przepływający w jednostkowym czasie. Aby obliczyć całkowitą energię wnikającą do naszego rezystora, należy przemnożyć strumień S przez powierzchnię, co jest też łatwe, ponieważ przyjęliśmy bardzo prostą geometrię pozwalającą na korzystanie z „okoliczności symetrii”. Należy jeszcze stwierdzić, czy energia faktycznie wnika do naszego rezystora, czy ewentualnie przez zewnętrzną powierzchnię nie „wycieka”. Kierunek S określa „umowa” będąca regułą iloczynu wektorowego. I łatwo stwierdzić, iż S jest w każdym punkcie prostopadły do powierzchni zewnętrznej naszego walca i skierowany do jego wnętrza. Iloczyn strumienia „wiatru Poyntinga” przez powierzchnię wynosi więc: S×2πrL=E×H×2πrL=U/L×I/2πr×2πrL. To po skróceniu oczywiście daje iloczyn U×I. Zastanówmy się przez chwilę, co policzyliśmy. Policzyliśmy całkowity strumień energii wnikającej (z otoczenia) do rezystora przez jego zewnętrzną powierzchnię w jednostce czasu. Energia w jednostce czasu, to moc! I wyszło nam U×I. Czyli „wiatr” Poyntinga faktycznie niesie tyle energii, ile wynika z prawa Joule’a. I moc która wnika do tego rezystora równa jest ilości ciepła, które się w nim wydzieli!

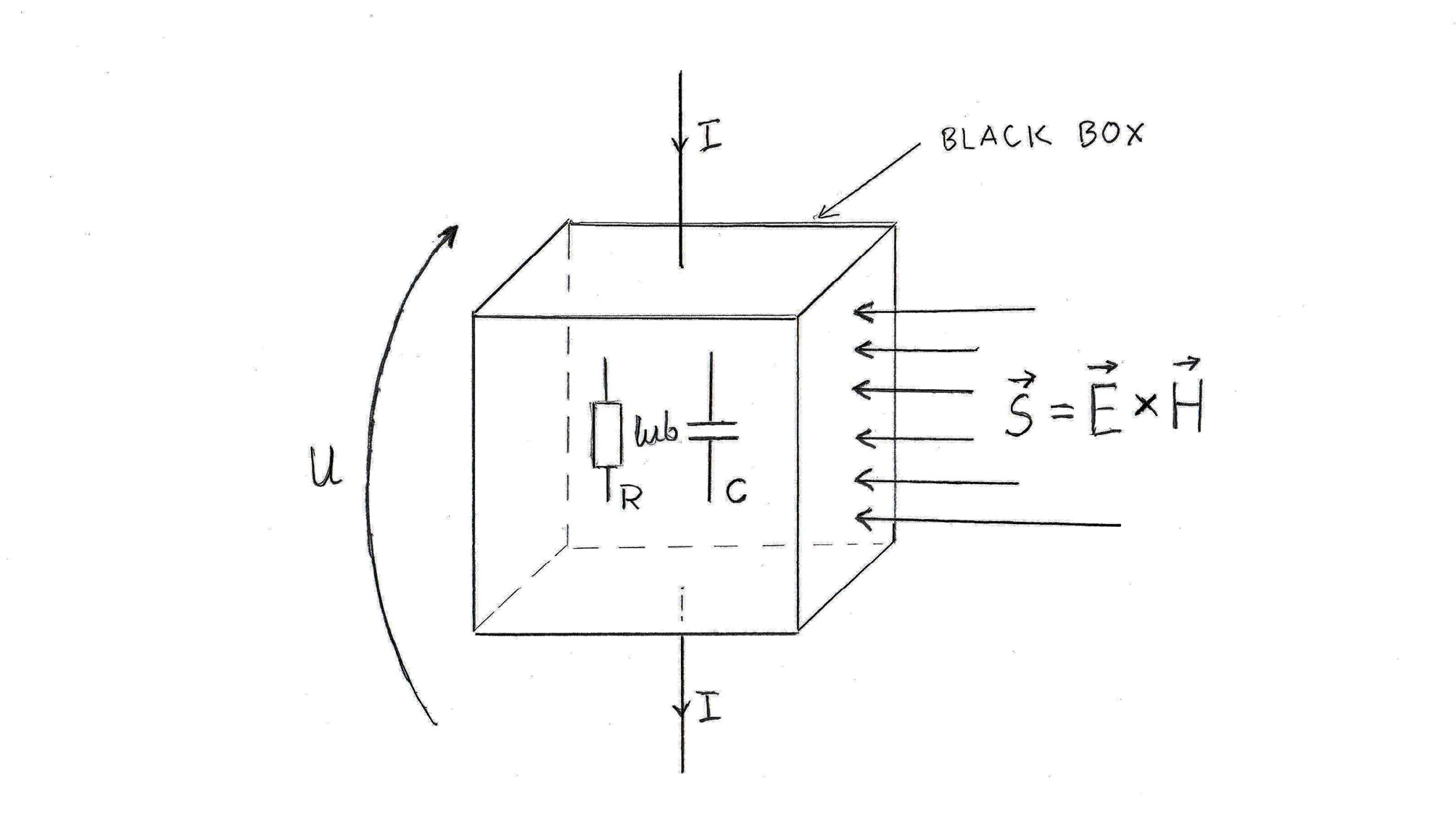
Weźmy teraz przypadek trochę bardziej skomplikowany. Załóżmy, że mamy do czynienia z kondensatorem, a nie opornikiem (rezystorem). Chcemy sprawdzić, czy ilość energii, która wnika do kondensatora z otaczającej go przestrzeni zgadza się z ilością energii, którą nasz kondensator gromadzi.
(…)

——– ciach! ——–

To jest tylko fragment artykułu, którego pełna wersja ukazała się w marcowym numerze czasopisma Zrozumieć Elektronikę (ZE 3/2025). Pełną wersję czasopisma znajdziesz pod tym linkiem. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 3/2025 znajduje się tutaj.

Karol Świerc
rtv@silnet.pl

 

Uwaga! Osoby, które nie są (jeszcze) stałymi Patronami ZE, mogą nabyć PDF-y z pełną wersję tego numeru oraz wszystkich innych numerów czasopisma wydanych od stycznia 2023, „stawiając kawę” (10 złotych za jeden numer czasopisma w postaci pliku PDF).
W tym celu należy kliknąć link (https://buycoffee.to/piotr-gorecki), lub poniższy obrazek

Następnie wybrać – Postaw kawę za:
– jeśli jeden numer ZE – 10 zł,
– jeśli kilka numerów ZE – Własna kwota. I tu wpisać kwotę zależną od liczby zamawianych numerów – wydań (N x 10 zł),
Wpisać imię nazwisko.
Podać adres e-mail.
Koniecznie zaznaczyć: „Chcę dodać dedykację/Wiadomość dla Twórcy” i tu wpisać, który numer lub numery ZE mam wysłać na podany adres e-mailowy. Jeśli ma to być numer z tym artykułem trzeba zaznaczyć, że chodzi o ZE 3/2025.
UWAGA!!! E-mail z linkiem do materiałów (Smash) wysyłamy zazwyczaj w ciągu 24 godzin. Czasem zdarza się jednak, że trafia do spamu. Jeśli więc nie pojawi się w ciągu 48 godzin prosimy sprawdzić w folderze spam, a ewentualny problem zgłosić na adres: kontakt@piotr-gorecki.pl.