Filtry aktywne – część 7

W poprzednim odcinku zajmowaliśmy się filtrami górnoprzepustowymi. W najbliższych dwóch odcinkach zajmiemy się filtrami dolnoprzepustowymi.

Jak zwykle na początku umieściłem gotowe proste recepty dla niecierpliwych praktyków, a do tego przykłady rachunkowe. W dalszej części bardziej zaawansowani znajdą ogólne wzory, nieco bardziej skomplikowane, ale za to pozwalające dobrać dodatkowe parametry.

Aby w pełni skorzystać z podanego materiału, konieczne jest przyswojenie sobie informacji ze wszystkich odcinków wstępnych, począwszy od pierwszego artykułu cyklu.

Filtr dolnoprzepustowy z wielokrotnym sprzężeniem zwrotnym

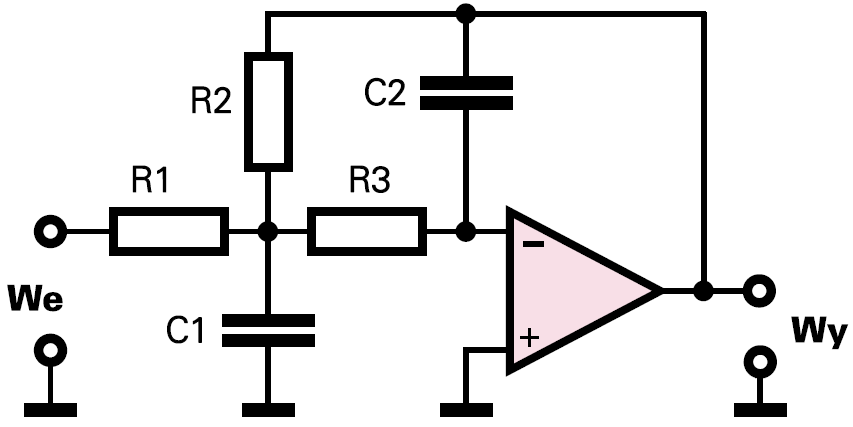
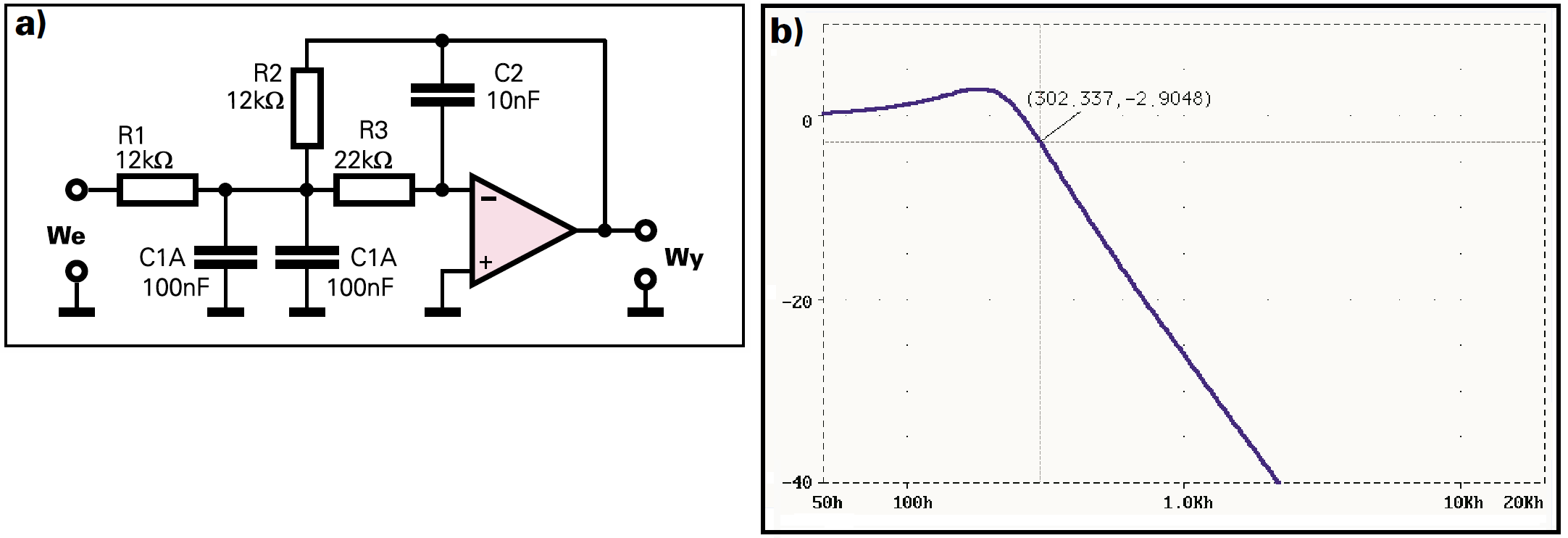
Możesz wykorzystać schemat z rysunku 1.

Mając daną częstotliwość graniczną f najpierw określisz sensowną wartość pojemności ze wzoru:

C [nF] = 3000 [nFHz] / f [Hz]

Najbliższa wartość z szeregu E6 to pojemność C2.

Teraz obliczysz reaktancję kondensatora C2 przy częstotliwości granicznej:

Reaktancja wychodzi w kiloomach, jeśli częstotliwość podasz w hercach, a pojemność w nanofaradach. Teraz możesz obliczyć pozostałe elementy.

Uwaga! Zwróć uwagę na różne wartości kondensatorów.

Dla dobroci 0,5:
R1 = R2 = X_c × 0,0675     R3 = X_c × 0,61     C1 = 10 × C2
Dla dobroci 0,707:
R1 = R2 = X_c × 0,19     R3 = X_c × 0,61     C1 = 10 × C2
W tych dwóch przypadkach pojemność C1 ma być dziesięciokrotnie większa niż C2.
Trochę inaczej będzie dla dobroci 1,35:
R1 = R2 = X_c × 0,23     R3 = X_c × 0,415     C1 = 20 × C2

Pojemność C1 ma być 20 razy większa niż C2. W praktyce warto połączyć równolegle dwa jednakowe kondensatory, każdy o pojemności 10 × C2, bo wtedy ewentualny błąd będzie bardzo mały.

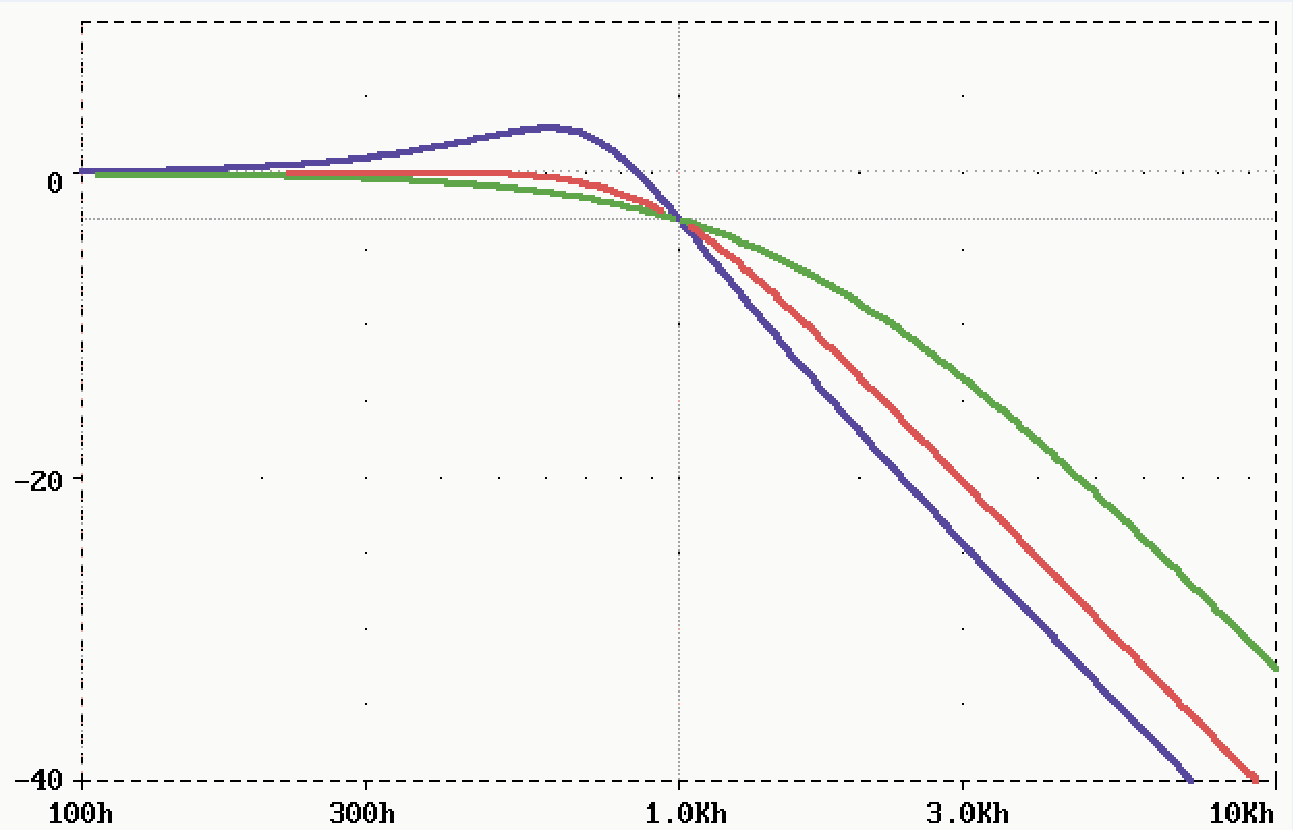
Rysunek 2 pokazuje charakterystyki filtrów o częstotliwości granicznej 1 kHz, obliczonych według podanych właśnie wzorów z rezystorami o dokładnych wartościach obliczonych ze wzoru.

We wszystkich przypadkach pojemność C2 wynosi 3,3 nF, natomiast wartości rezystorów wynoszą:
Q=0,5: R1=R2=3,27 kΩ, R3=29,6 kΩ, C1=33 nF
Q=0,707: R1=R2=9,21 kΩ, R3=29,6 kΩ, C1=33 nF
Q=1,35: R1=R2=11,1 kΩ, R3=20,1 kΩ, C1=66 nF

Kto chce, może żmudnie dobierać rezystory, jeśli koniecznie chce uzyskać dokładne wartości wyliczone ze wzorów, ale nie ma to żadnego sensu, jeśli zastosowane kondensatory mają tolerancję 10% lub 5%. Należy po prostu wziąć najbliższe nominały z szeregu 1−procentowego, albo jeśli ktoś nie ma takich możliwości, nawet z szeregu 5−procentowego. Drobne różnice wartości uzyskanej częstotliwości granicznej rzędu kilku procent w większości przypadków nie mają żadnego znaczenia.

Przykłady

Obliczmy teraz przykładowy filtr audio do obcięcia częstotliwości ponadakustycznych o częstotliwości granicznej 16 kHz i dobroci 0,707. Korzystamy ze wzoru:
C [nF] = 3000 [nFHz] / 16000 [Hz]
i…
pojemność wychodzi żałośnie mała, mniejsza od 200 pF. Jak już wiesz, możemy dowolnie wybrać wartość tej pojemności. Niech będzie równa 470 pF − to pojemność C2. A teraz normalnie liczymy dalej. Obliczamy reaktancję kondensatora C2 przy częstotliwości granicznej:
X_c [kΩ] = 160000 / (16000 [Hz] × 0,47 [nF])
X_c = 21,3 kΩ
i dalej:
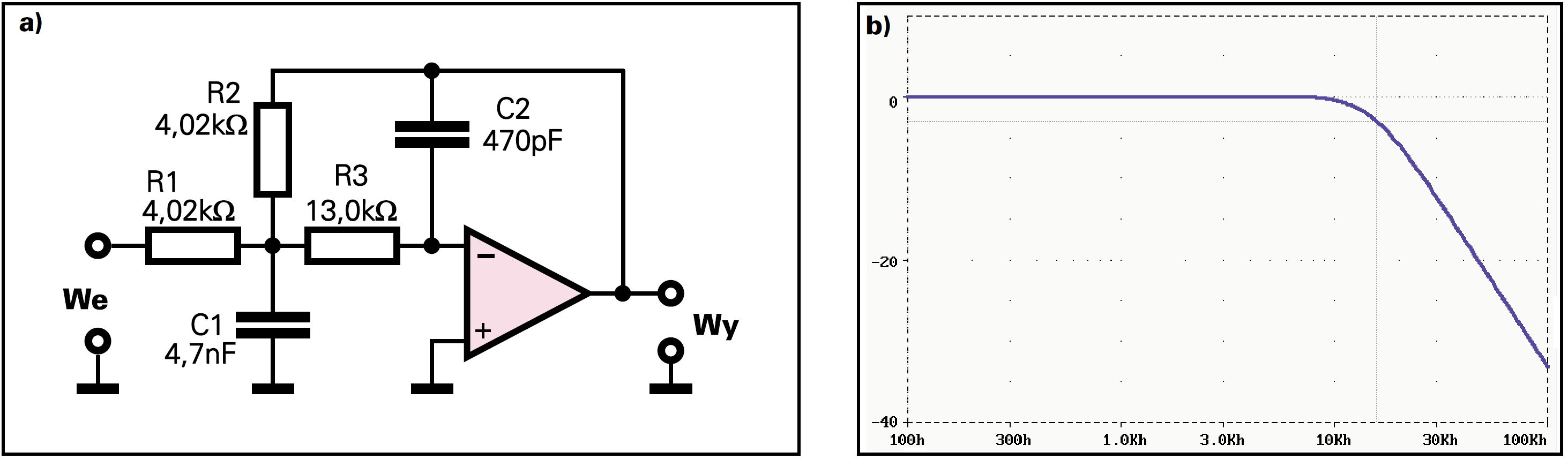
R1 = R2 = 21,3 × 0,19 = 4,05 kΩ     R3 = 21,3 × 0,61 = 13 kΩ     C1 = 10 × 0,47 = 4,7nF

Zastosujemy rezystory 1−procentowe: 4,02 kΩ i 13,0 kΩ. Układ i charakterystyki pokazane są na rysunku 3.

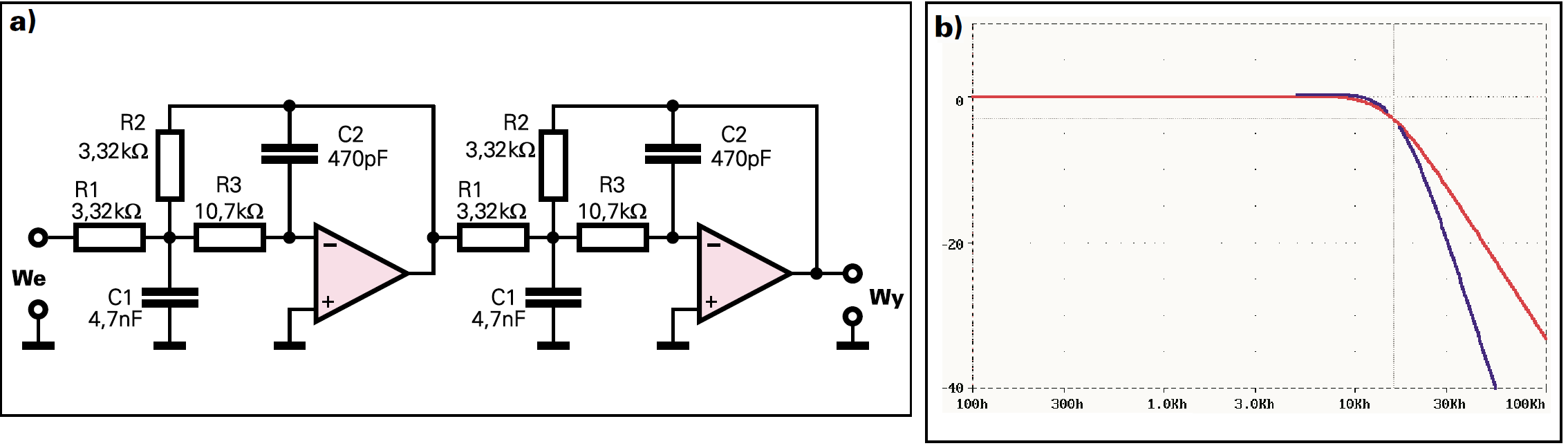
Jeśli potrzebna jest większa stromość, połączymy w szereg dwa filtry, co oczywiście spowoduje przesunięcie (w dół) 3−decybelowej częstotliwości granicznej. Przesuniemy więc w górę częstotliwości, zmniejszając wartość rezystorów 1,2−krotnie. Schemat i charakterystyki pokazane są na rysunku 4.

Zaprojektujmy jeszcze filtr do iluminofonii o częstotliwości granicznej 300 Hz i dobroci 1,35.
C [nF] = 3000 [nFHz] / 300 [Hz]
C = C2 =10 nF
X_c [kΩ] = 160000 / (300 [Hz] × 10 [nF])
X_c = 53,3 kΩ i dalej:
R1 = R2 = 53,3 × 0,23 = 12,26 kΩ     R3 = 53,3 × 0,415 = 22,12 kΩ     C1 = 20 × 10 nF =200 nF

Stosujemy popularne rezystory z szeregu E24: 12 kΩ i 22 kΩ i dwa kondensatory 100 nF w roli C1. Układ i charakterystyki tego filtru pokazuje rysunek 5.

Dla zaawansowanych i dociekliwych

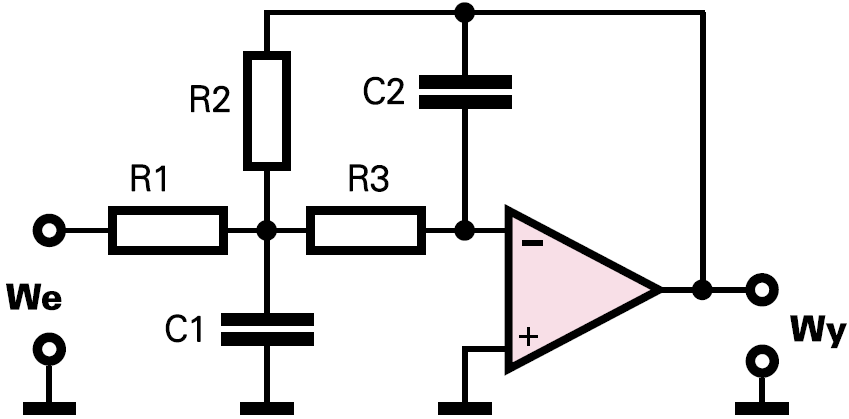
Kto ma ochotę się pobawić, może przeprowadzić pełniejszą procedurę projektową. Nadal rozpatrujemy filtr według rysunku 6. Do obliczeń potrzebne są wartości:
fg − częstotliwości granicznej
Q − dobroci
G − wzmocnienia

Jak zawsze, na początek dobieramy sensowną pojemność z szeregu E6 zbliżoną do wartości:
C [nF] = 3000 [nFHz] / f [Hz]

To będzie pojemność C2. Obliczamy reaktancję kondensatora C2 przy częstotliwości granicznej:

Tym razem do uproszczenia obliczeń wykorzystamy dodatkową stałą K. Będzie to dowolnie wybrana liczba spełniająca warunek:
K > 4Q² (G+1)

Zazwyczaj będzie to liczba całkowita, na przykład równa 10. Stałą K wybierzemy tak, by uzyskać sensowną wartość C1:
C1 = K × C2
Potem policzymy:

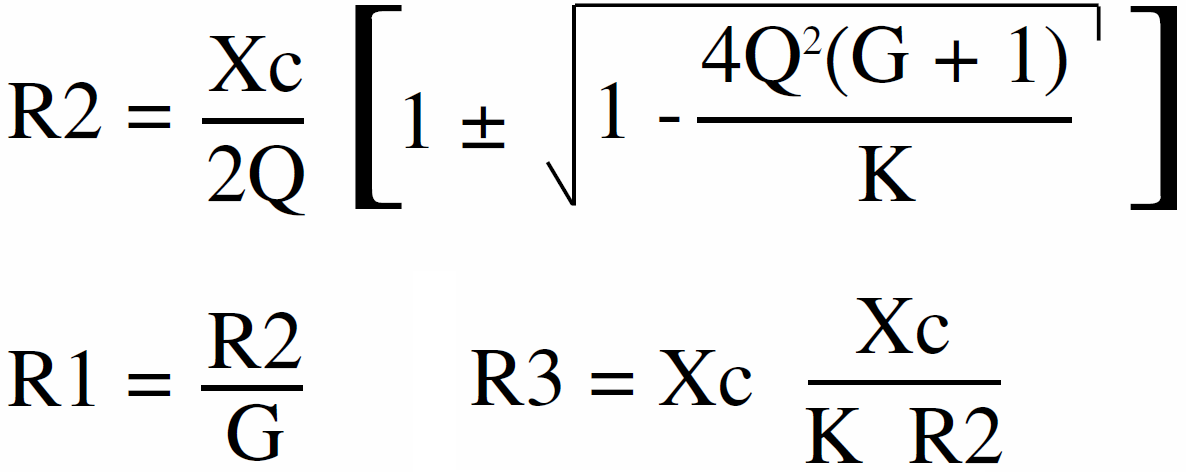
Wzór na R2 wydaje się co najmniej dziwny, bo daje dwie różne wartości R2, ale nie jest to błąd. Jeśli chcesz, zastosuj te wzory, możesz też przeprowadzić symulację komputerową, jeśli masz stosowny program. Tak czy inaczej, w ogromnej większości przypadków wystarczy korzystać z podanych wcześniej uproszczonych recept.

A w kolejnym odcinku omówimy filtry dolnoprzepustowe Sallen−Keya.

Piotr Górecki