Filtry aktywne – część 6

Kontynuujemy omawianie filtrów górnoprzepustowych drugiego rzędu, o stromości 12 dB/oktawę (40 dB/dekadę). Zaczęliśmy je omawiać w poprzednim odcinku. W tym wykładzie zajmiemy się popularnymi filtrami Sallen−Keya, nazywanymi też filtrami VCVS (voltage controlled voltage source − źródło napięciowe sterowane napięciem).

Znów na początku umieściłem gotowe proste recepty dla niecierpliwych praktyków. Dalej zaprezentowane są przykłady rachunkowe. W końcowej części odcinka przedstawione są ogólne wzory, nieco bardziej skomplikowane, ale za to pozwalające dobrać dodatkowe parametry.

Aby w pełni skorzystać z podanego materiału, konieczne jest przyswojenie sobie informacji ze wszystkich odcinków wstępnych, począwszy od pierwszego artykułu cyklu.

Filtr górnoprzepustowy ze źródłem sterowanym (Sallen−Keya)

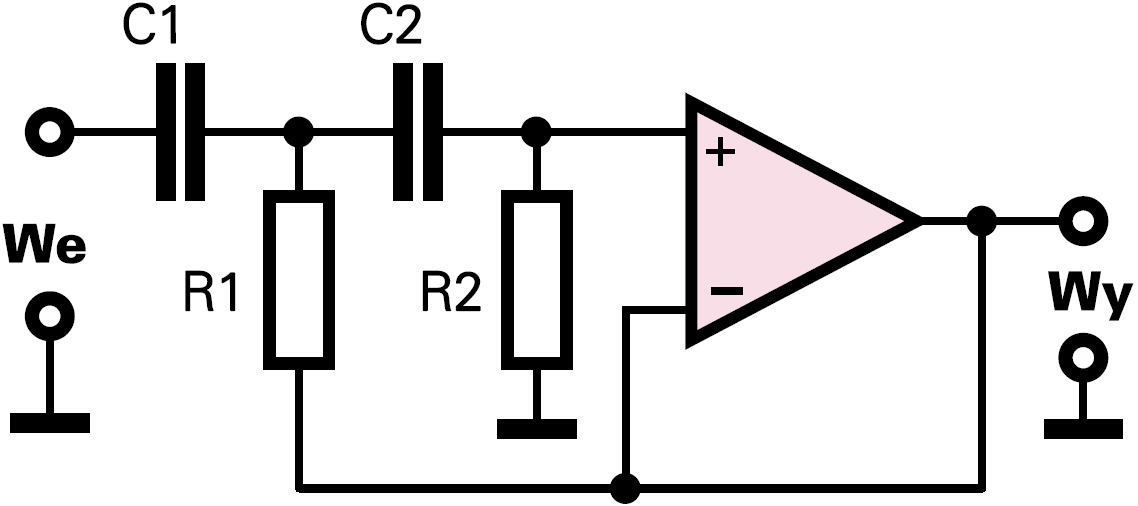
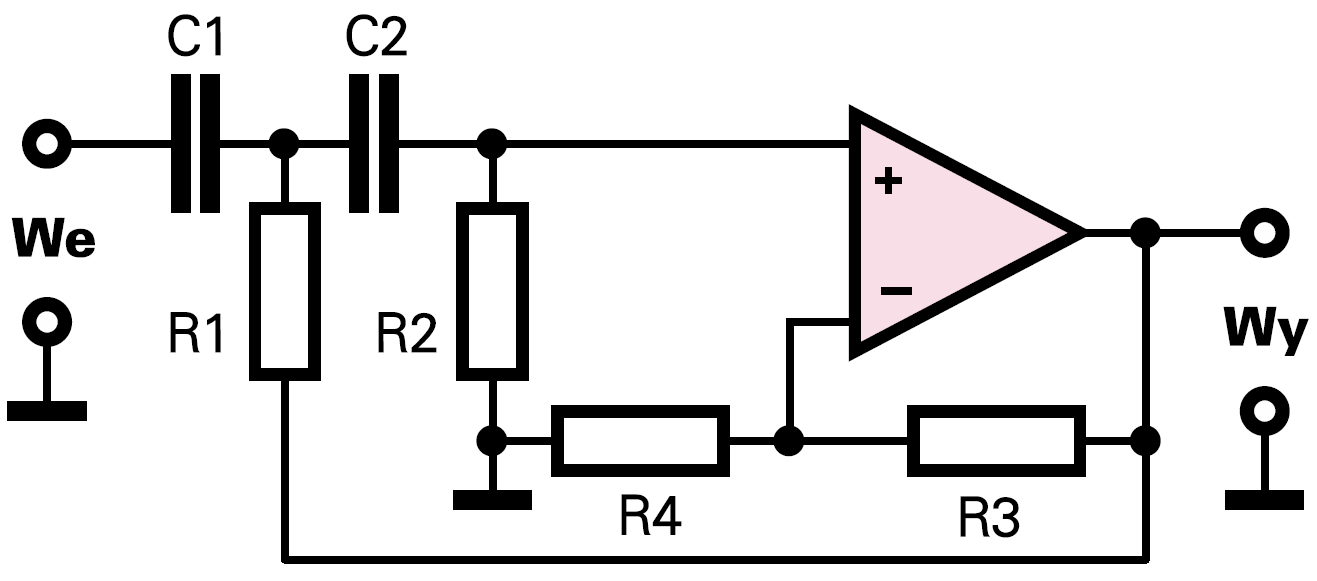
Zamiast omawianego w poprzedniej części filtru MFB możesz wykorzystać nieco prostszy filtr Sallen−Keya z rysunku 1.

Podobnie jak poprzednio, najpierw wybierzesz sensowną wartość pojemności korzystając ze wzoru:
C [nF] = 10000 [nFHz] / f [Hz]
i wybierzesz najbliższą wartość z szeregu E6.
Masz już wartości C1 i C2.

Teraz obliczysz reaktancję przy częstotliwości granicznej fg:

Nie zapominając, że oporność uzyskasz w kiloomach, jeśli częstotliwość będzie w hercach, a pojemność w nanofaradach.

Mając C1=C2=C obliczasz wartości R1 i R2:
Dla dobroci 0,5:
R1 = X_c × 1,55     R2 = X_c × 1,55
Dla dobroci 0,707:
R1 = X_c × 0,707     R2 = X_c × 1,41
Dla dobroci 1,35 (podbicie +3 dB):
R1 = X_c × 0,275     R2 = X_c × 1,85

To wszystko!

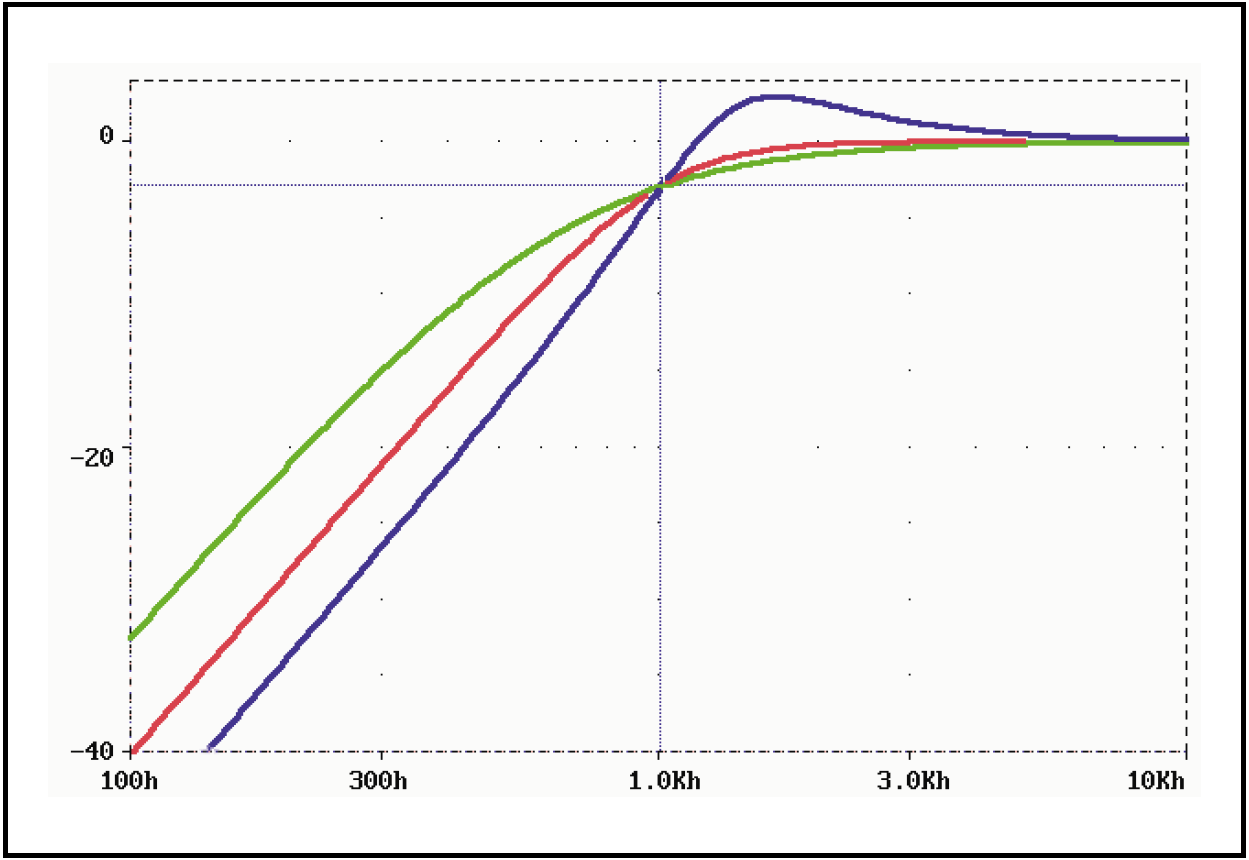
Rysunek 2 pokazuje przebieg charakterystyk amplitudowych filtrów o częstotliwości granicznej 1 kHz obliczonych według podanych właśnie wzorów gdy C1=C2=10 nF.
Rezystory mają wartości:
Q=0,5: R1=24,7 kΩ, R2=24,7 kΩ,
Q=0,707: R1=11,31 kΩ, R2=22,61 kΩ,
Q=1,35: R1=4,4 kΩ, R2=29,6 kΩ.

Przykłady

Aby utrwalić uzyskane informacje, obliczmy teraz elementy filtru górnoprzepustowego Sallen−Keya o częstotliwości granicznej 7 kHz. Przypuśćmy, że taki filtr potrzebny jest do konstruowanego właśnie urządzenia iluminofonicznego. Tym razem chcemy uzyskać jak największe tłumienie i dopuszczamy niewielkie podbicie charakterystyki, dlatego przyjmujemy dobroć 1,35. Dobieramy pojemność:
C [nF] = 10000 [nFHz] / 7000 [Hz]

Decydujemy się na najbliższą wartość z szeregu E6, czyli na 1,5 nF.
C=C1=C2=1,5 nF
X_c [kΩ] = 160000 / (7000 [Hz] × 1,5 [nF])     X_c [kΩ] = 15,24 kΩ
Obliczamy rezystory:
R1 = 0,275 × 15,24 kΩ = 4,19 kΩ     R2 = 1,85 × 15,24 kΩ = 28,19 kΩ
Stosujemy najbliższe wartości z szeregu E24:
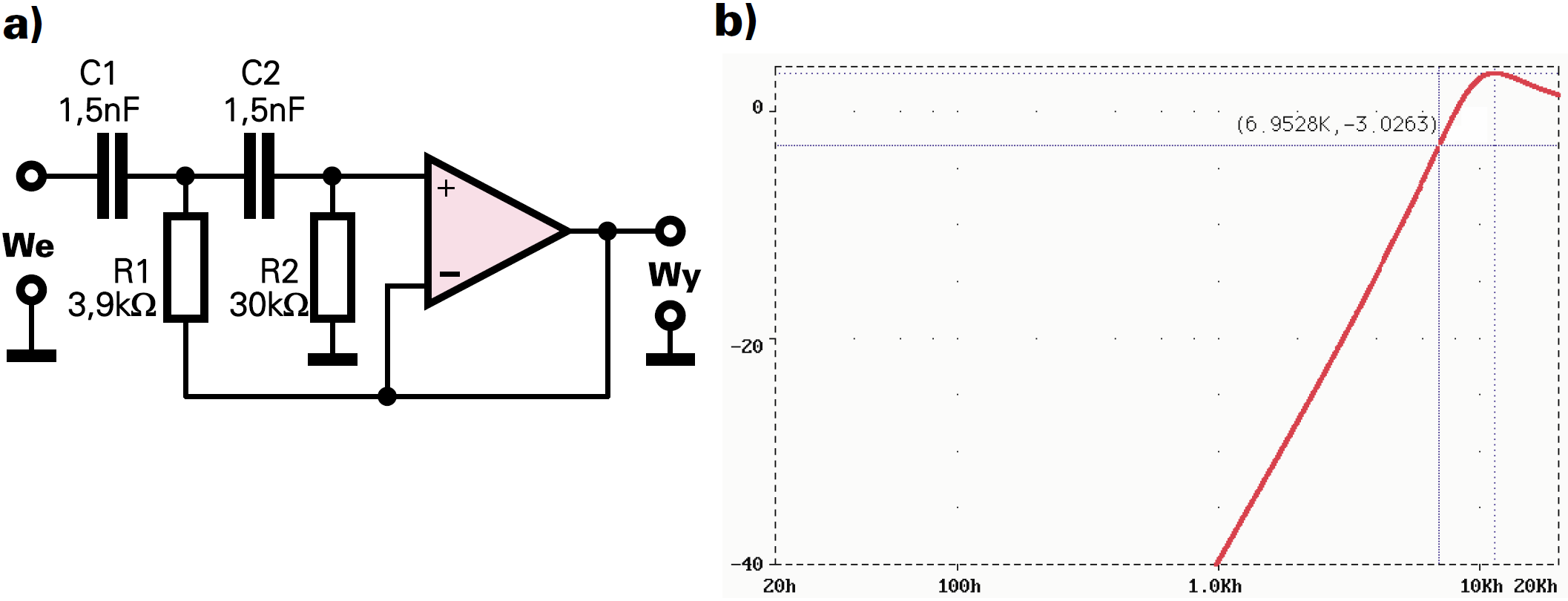
R1 = 3,9 kΩ     R2 = 30 kΩ

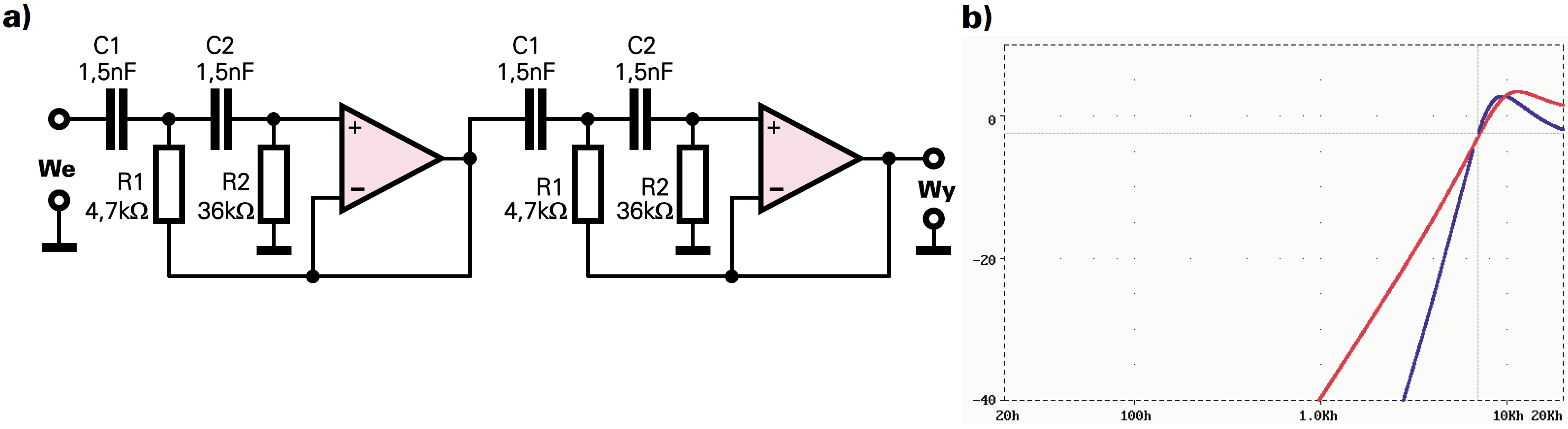
Na rysunku 3a i b zobaczysz układ i charakterystykę tak obliczonego filtru. Do urządzenia iluminofonicznego taka stromość wystarczy, ale jeśli ktoś koniecznie chciałby uzyskać dwa razy większą stromość, może połączyć dwa filtry. Podobnie jak było w przypadku omawianego wcześniej filtru MFB, także i teraz częstotliwość graniczna przesunie się w górę. Obniżymy ją do pożądanej wartości, jeśli zastosujemy mniej więcej 1,2 razy większe wartości rezystorów (R1=4,7 kΩ, R2=36 kΩ).

Rysunek 4a,b pokazuje schemat i charakterystyki. Linia czerwona to charakterystyka wcześniej obliczonego pojedynczego filtru podana tu dla porównania, a linia niebieska pokazuje charakterystykę amplitudową podwójnego filtru, przy czym dla łatwiejszego porównania obniżyłem ją o 4 dB. W praktyce oznacza to, że podwójny filtr zapewni dodatkowo niewielkie wzmocnienie w paśmie przepustowym.

Dla zaawansowanych i dociekliwych

Podane sposoby obliczania filtru drugiego rzędu są znów wyjątkowo proste i przyjazne, ale też nie pozwalają w pełni wykorzystać możliwości danej konfiguracji. Jeśli ktoś chce, może skorzystać z nieco bardziej skomplikowanej procedury projektowej. Znów znajdziemy wartości elementów dla dowolnych wartości częstotliwości, dobroci i dowolnego wzmocnienia. Do obliczeń wykorzystamy wartości:
fo − częstotliwości granicznej
Q − dobroci
G − wzmocnienia.

Tym razem, ze względu na zmienną wartość wzmocnienia musimy dodać dwa rezystory i układ będzie wyglądał jak na rysunku 5.

Obliczenia

Znów na początek dla ułatwienia przyjmujemy, że C1=C2 i wybieramy wartość:
C [nF] = 10000 [nFHz] / f [Hz]

Pojemność wychodzi w nanofaradach, jeśli częstotliwość podamy w hercach. Wybieramy najbliższą wartość z szeregu.
Mamy już C1=C2=C

Obliczamy reaktancję wybranego kondensatora przy częstotliwości granicznej:

podstawiając wybraną wartość pojemności z szeregu, a nie wartość obliczoną wcześniej ze wzoru. Reaktancja wychodzi w kiloomach, jeśli częstotliwość podamy w hercach, a pojemność w nanofaradach.

Rezystory R3, R4 wyznaczają wzmocnienie jak w zwykłym wzmacniaczu nieodwracającym:

Teraz obliczamy wartości pozostałych elementów w zależności od dobroci filtru i wzmocnienia:

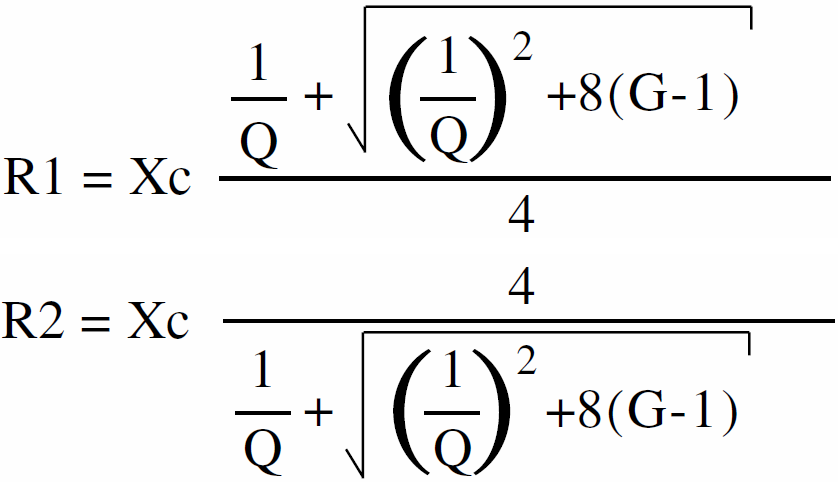
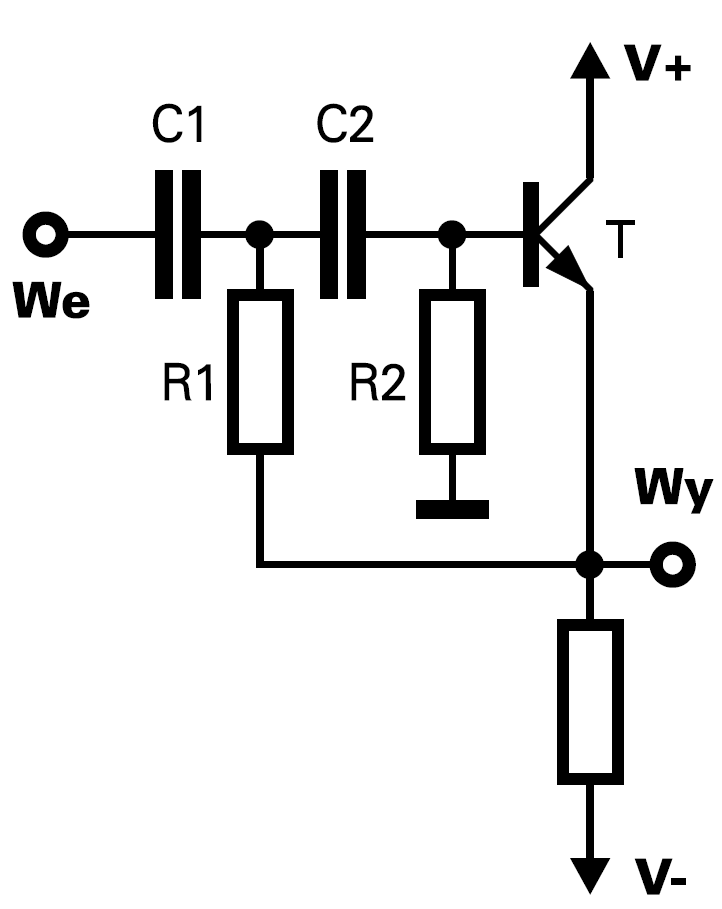
Rysunek 5 i podane wzory przekonują, że w przypadku konieczności realizacji filtru o wzmocnieniu większym od jedności lepiej jest wykorzystać filtr MFB, omawiany w poprzednim odcinku. Górnoprzepustowy filtr Sallen−Keya jest natomiast używany bardzo często, jeśli wzmocnienie jest równe 1. Warto zauważyć, że nie musi tu być stosowany wzmacniacz operacyjny − wystarczy jakikolwiek wtórnik o wzmocnieniu 1. W mniej odpowiedzialnych zastosowaniach zamiast wzmacniacza operacyjnego wykorzystuje się czasem tranzystor według idei pokazanej na rysunku 6.

Tyle o filtrach górnoprzepustowych. W kolejnym wykładzie zajmiemy się filtrami dolnoprzepustowymi.

Piotr Górecki