Filtry aktywne – część 8
W poprzednim odcinku zajmowaliśmy się filtrami dolnoprzepustowymi z wielokrotnym sprzężeniem zwrotnym. W tym odcinku zajmiemy się filtrami dolnoprzepustowymi Sallen−Keya.
Z filtrami dolnoprzepustowymi tego typu jest pewien kłopot. Przy wzmocnieniu równym 1 trudno jest uzyskać dobroć większą niż 0,5. Aby nie zrazić Cię do tych filtrów podaję dwie procedury projektowe. W dalszej części bardziej zaawansowani znajdą ogólne wzory, nieco bardziej skomplikowane, ale za to pozwalające dobrać dodatkowe parametry.
Aby w pełni skorzystać z podanego materiału, konieczne jest przyswojenie sobie informacji ze wszystkich odcinków wstępnych, począwszy od pierwszego artykułu cyklu.
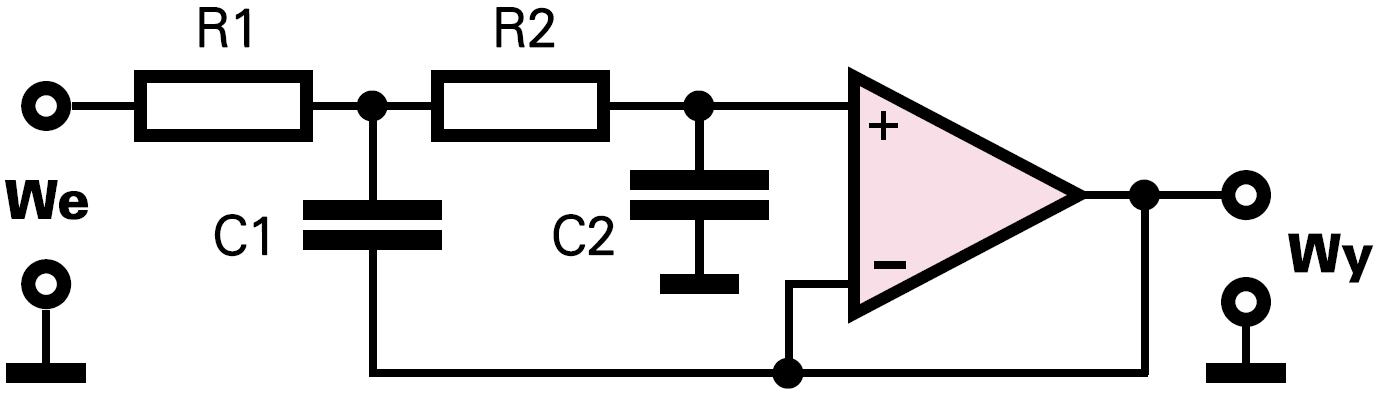
Filtr dolnoprzepustowy Sallen−Keya. Wersja 1
Filtr dolnoprzepustowy zrealizujesz także według rysunku 1.
Jak zwykle, najpierw wybierasz sensowną wartość pojemności. Jeśli filtr ma mieć dobroć 0,707 korzystasz ze wzoru:
C [nF] = 3000 [nFHz] / f [Hz]
i wybierasz najbliższą wartość z szeregu E6. Obliczyłeś tym sposobem wartość C2.
Teraz obliczasz reaktancję C2 przy częstotliwości granicznej fg:
![]()
nie zapominając, że oporność uzyskasz w kiloomach, jeśli częstotliwość będzie w hercach, a pojemność w nanofaradach.
Następnie obliczasz wartości R2 i R1:
Dla dobroci 0,707:
R1 = Xc × 0,088 R2 = Xc × 1,32
Dla Q=1,35 (podbicie +3dB):
R1 = Xc × 0,225 R2 = Xc × 0,845
Pojemność C1 jest dla obu filtrów dziesięciokrotnie większa od C2:
C1 = 10 × C2
I to wszystko!
Dla Q=0,5, zadanie jest jeszcze łatwiejsze:
C [nF] = 10000 [nFHz] / f [Hz]
Wybierasz najbliższą wartość z szeregu. Masz już wartości C1, C2.
C=C1=C2
Obliczasz reaktancję przy częstotliwości granicznej:
![]()
i jednakowe wartości R1 i R2:
R1 = Xc × 0,65 R2 = Xc × 0,65
Koniec!
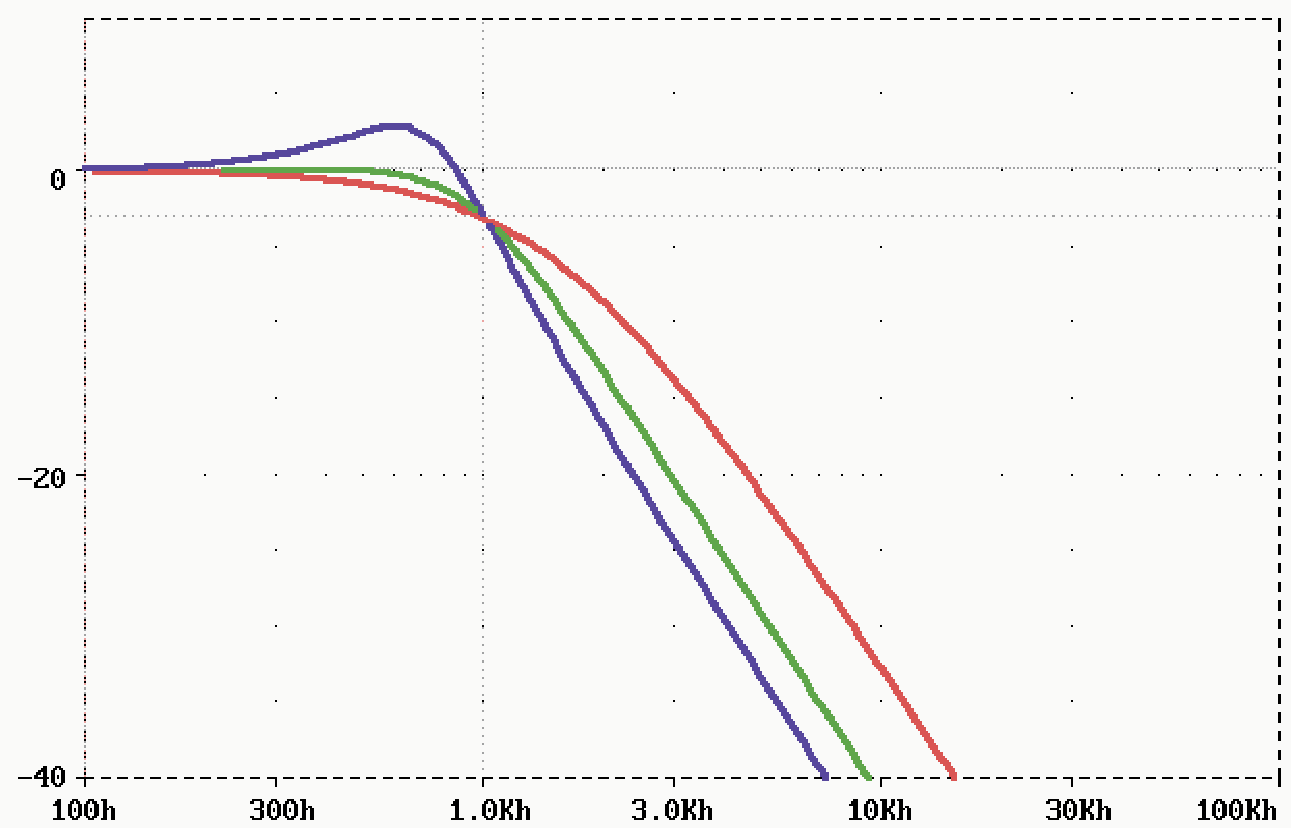
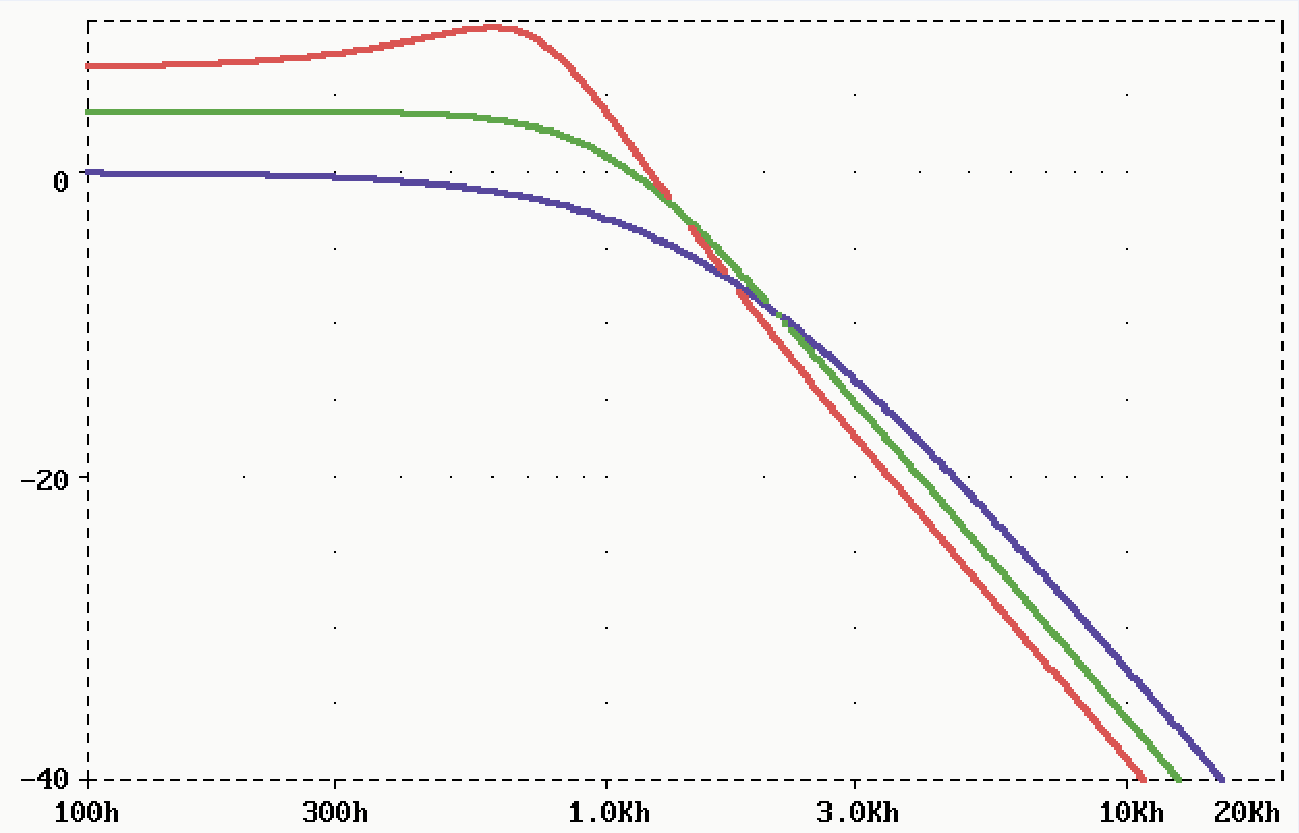
Rysunek 2 pokazuje charakterystyki takich filtrów o częstotliwości granicznej 1 kHz, obliczonych według podanych właśnie wzorów z rezystorami o dokładnych wartościach obliczonych ze wzoru.
Wartości elementów wynoszą:
Q=0,5: R1=R2=10,4 kΩ, C1=C2=10 nF
Q=0,707: R1=4,24 kΩ, R2=63,7 kΩ,
C1=33 nF, C2=3,3 nF
Q=1,35: R1=10,9 kΩ, R2=40,7 kΩ, C1=33 nF, C2=3,3 nF
Przykład
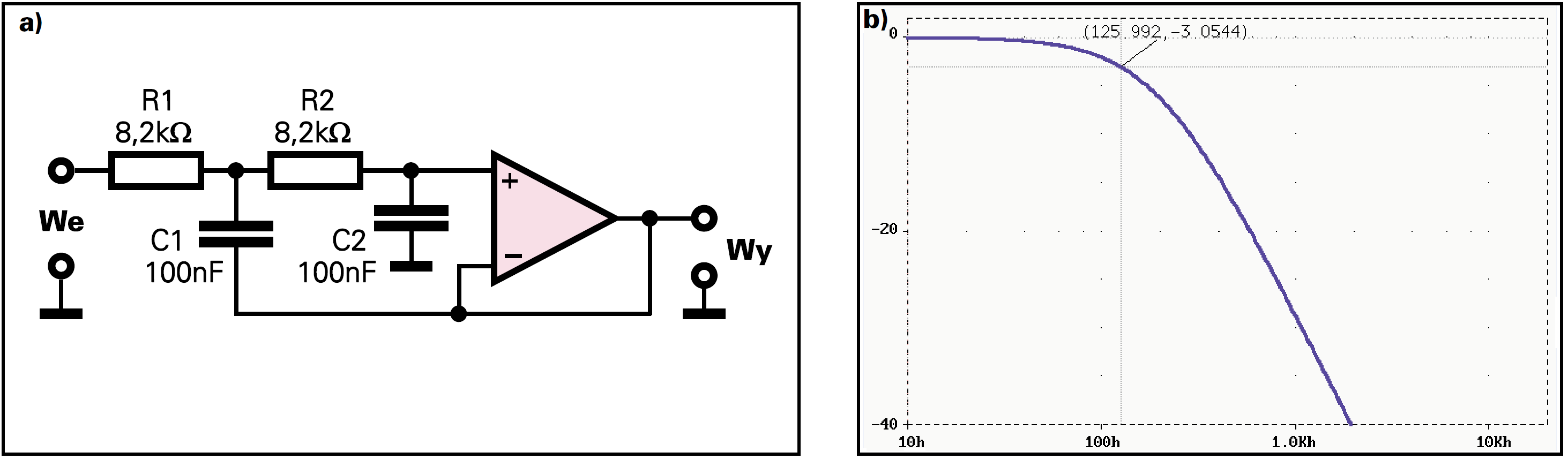
Obliczmy elementy filtru do subwoofera, dolnoprzepustowego, Sallena−Keya o częstotliwości granicznej 120 Hz i dobroci 0,5. Decydujemy się na dobroć 0,5, by uzyskać dobrą charakterystykę fazową, potrzebną do w miarę wiernego przenoszenia impulsów.
C [nF] = 10000 [nFHz] / 120 [Hz]
C=83 nF
Wybieramy najbliższą popularną wartość z szeregu − 100 nF. Masz już wartości C1, C2.
C=C1=C2=100 nF
Xc [kΩ] = 160000 / (120 [Hz] × 100 [nF])
Xc = 13,3 kΩ
stąd
R1 = R2 = 0,65 × 13,3 = 8,66 kΩ
Stosujemy 5−procentowy rezystor 8,2 kΩ. Układ i charakterystykę pokazuje rysunek 3.
Ze względu na nieco mniejszą wartość rezystorów (8,2 kΩ, zamiast 8,66 kΩ), częstotliwość graniczna jest nieco wyższa od założonej i wynosi około 126 Hz.
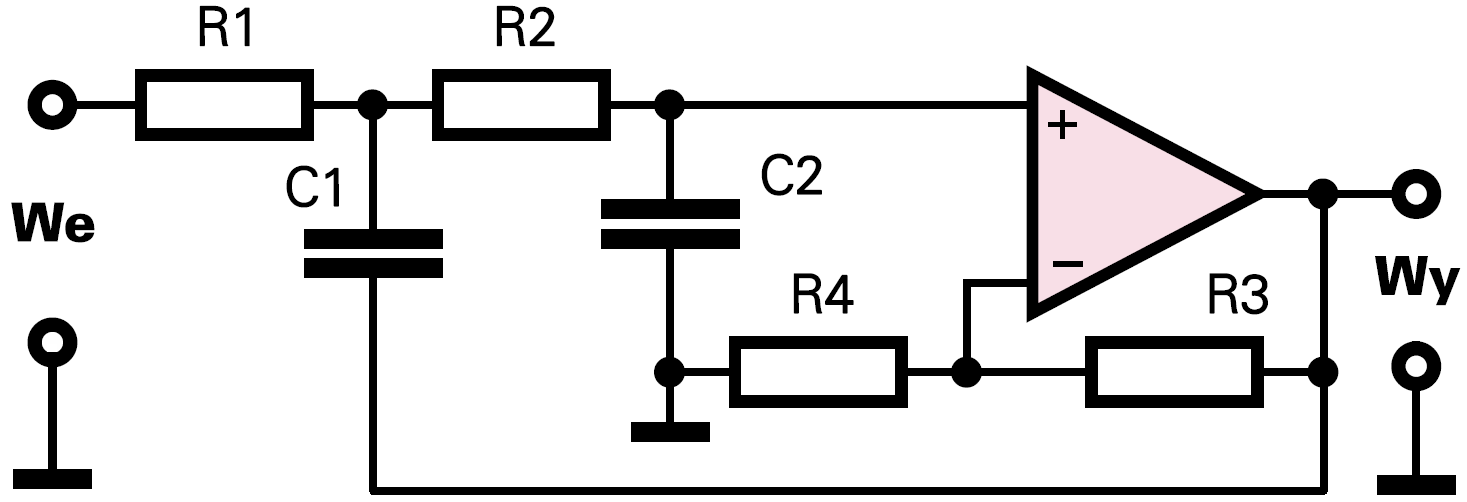
Filtr dolnoprzepustowy Sallen−Keya. Wersja 2
Schemat z rysunku 4 pozwala w prosty sposób zrealizować filtr o dowolnej dobroci.
Zaletą jest to, że rezystory R1, R2 i kondensatory C1, C2 są jednakowe. Dobroć zwiększamy powyżej 0,5, zwiększając wzmocnienie wzmacniacza za pomocą dodatkowych rezystorów R3, R4.
Procedura jest typowa:
Mając fg obliczamy:
C [nF] = 10000 [nFHz] / f [Hz]
Dobieramy C=C1=C2 jako najbliższą wartość z szeregu.
Następnie obliczamy:
![]()
Dla Q=0,5 jak poprzednio:
R1 = Xc × 0,65 R2 = Xc × 0,65 R3 – zwora R4 – nie stosować
Dla Q=0,707:
R1 = Xc R2 = Xc R3 = 0,59 × R4 (np. 5,9 kΩ) R4 − np. 10 kΩ
Dla Q=1,35:
R1 = Xc × 1,37 R2 = Xc × 1,37 R3 = 1,2 × R4 (np. 12 kΩ) R4 − np. 10 kΩ
Wartość R4 nie musi być taka, jak podano wyżej, ale należy zachować podane wartości wzmocnienia. Oczywiście filtr o dobroci powyżej 0,5 przy okazji wzmocni sygnały w paśmie przepustowym:
Q=0,707 − wzmocnienie 1,59× czyli o 4 dB,
Q=1,35 − wzmocnienie 2,2× czyli o 6,85 dB.
Rysunek 5 pokazuje charakterystyki takich filtrów.
Jak widać, filtr o dobroci 1,35 najbardziej wzmacnia sygnały użyteczne, a jednocześnie najlepiej tłumi sygnały spoza pasma przenoszenia. Nie znaczy to jednak, że we wszystkich przypadkach okaże się najlepszy. Na przykład tam, gdzie istotna jest odpowiedź na sygnały impulsowe, korzystniejszy będzie filtr o mniejszej dobroci, bo ma liniową charakterystykę fazową.
Dla zaawansowanych i dociekliwych
Filtr z rysunku 4 można projektować stosując następującą procedurę.
Do obliczeń potrzebne są wartości:
fg − częstotliwości granicznej
Q − dobroci
G − wzmocnienia
![]()
Przy czym wzmocnienie ma być większe niż 2. Jak zawsze, na początek dobieramy sensowną pojemność z szeregu E6 zbliżoną do wartości:
C [nF] = 10000 [nFHz] / f [Hz]
Potem Xc
![]()
Następnie:
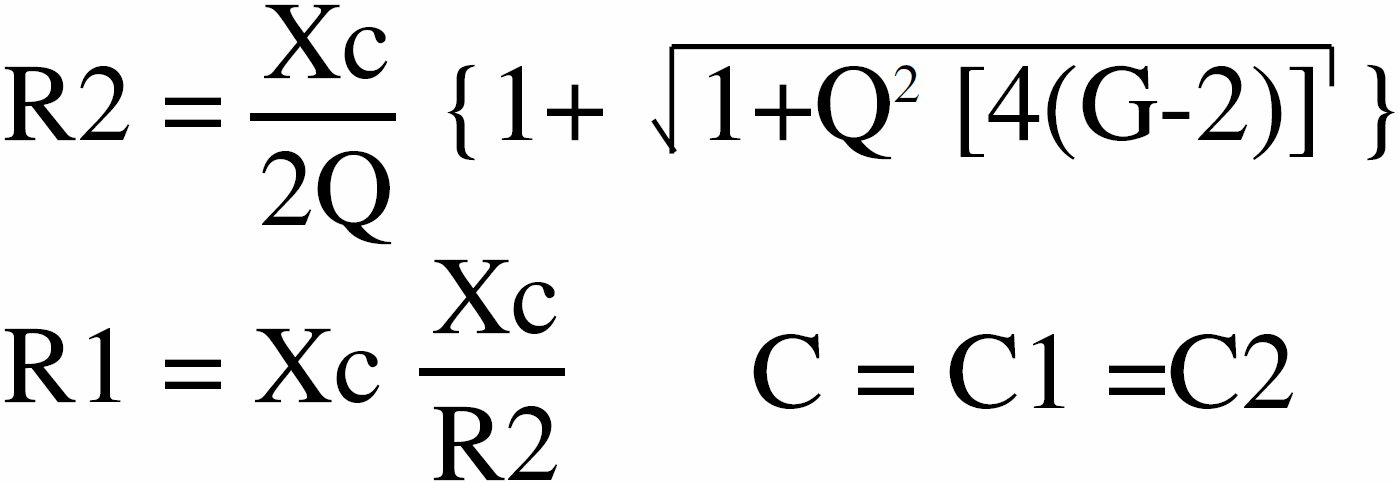
Tyle na temat filtrów dolnoprzepustowych. W następnym odcinku weźmiemy na warsztat filtry pasmowe.
Piotr Górecki