Elektronika (nie tylko) dla informatyków (10) Reaktancja – przypadek szczególny

W naszych wcześniejszych rozważaniach, odnosząc się również do poprzedniego wykładu doszliśmy do wniosku, że do obliczeń obwodów prądu zmiennego potrzebujemy sposobu precyzyjnego zapisu wartości impedancji w postaci jednej liczby, która zawierałaby informacje o wielkości oporności oraz jednocześnie o kącie przesunięcia fazy między prądem a napięciem. Taki precyzyjny zapis pozwoliłby przeprowadzić prawidłowe obliczenia przy użyciu tych samych wzorów, co w przypadku prądu stałego.

Zasygnalizowałem Ci już, że istnieją „dziwne liczby”, których reprezentacją graficzną są punkty płaszczyzny, a nie tylko prosta reprezentująca liczby rzeczywiste. Przyjrzyjmy się temu bliżej. Najpierw proponuję Ci garść informacji historycznych.

Trochę historii

Zapomnij na chwilę o reaktancji kondensatora. Porozmawiamy o liczbach, wymyślonych kilkaset lat temu przez teoretyków. Dziś są one nazywane liczbami zespolonymi (complex numbers). Ich początków należy upatrywać w kłopotach z rozwiązywaniem równań. Otóż zarówno starożytni Grecy, jak też później Arabowie, kontynuujący ich osiągnięcia, a także matematycy hinduscy i chińscy zajmowali się równaniami oraz geometrią. W XIII wieku, po kilkusetletnim okresie zastoju, matematyką zaczęto się zajmować także w Europie Zachodniej. W XVI wieku, a więc w epoce renesansu, na niektórych włoskich uniwersytetach zajmowano się m.in. rozwiązaniami (pierwiastkami) równań drugiego i trzeciego stopnia. Wydawało się, że niektóre równania nie mają rozwiązań. Warto mieć świadomość, że ówczesny poziom wiedzy w tej dziedzinie nie wykraczał wiele ponad matematykę dzisiejszej szkoły podstawowej i gimnazjum, gdzie też stwierdza się, iż niektóre równania drugiego stopnia nie mają rozwiązania, na przykład x² = -1. Jednak już XVI-wieczni matematycy próbowali zgłębić te zagadnienia i niektórzy zrywali z wcześniejszymi wyobrażeniami i dochodzili do wniosku, że istnieją „dziwne” pierwiastki równań. Należy tu wspomnieć o takich włoskich matematykach jak del Ferro, Antonio Maria Fiore, Niccolò Fontana, znany jako Tartaglia, czyli Jąkała, a przede wszystkim Girolamo Cardano (ten od przegubu Cardana), który pierwszy opisał w dziele Ars Magna, sive de regulis algebraicis ujemne rozwiązania równań i nazywał je liczbami fikcyjnymi lub „mniej czystymi pierwiastkami”. Wtedy był kłopot nawet z zaakceptowaniem istnienia liczb ujemnych, ale Cardano i inni wymienieni napotykali liczby „jeszcze dziwniejsze” od ujemnych. I właśnie uznaje się, że to Cardano jako pierwszy używał liczb zespolonych, choć zupełnie nie rozumiał ich właściwości, skoncentrowany raczej na zagadkach oraz graficznych reprezentacjach równań i ich rozwiązań.

Kolejny duży krok zrobił uczeń Cardana, Rafael Bombelli, który w roku 1572 oprócz liczb rzeczywistych dodatnich (più) i ujemnych (meno) pisał o liczbach più di meno i meno di meno, które dziś nazwalibyśmy liczbami zespolonymi. Potem Kartezjusz (Descartes), traktując je nie jako „prawdziwe” liczby, lecz liczby, które co najwyżej można sobie wyobrazić, nazywał je liczbami urojonymi (imaginary). Duży wkład w rozwój teorii liczb zespolonych miał znany XVIII wieku szwajcarski matematyk Euler (1707–1783). Teoria liczb zespolonych została w pełni sformułowana w pierwszej połowie XIX wieku, a wkład w to mieli głównie Caspar Wessel (1745–1818), Jean-Robert Argand (1768–1822) William Rowan Hamilton (1805–1865), Carl Friedrich Gauss (1777–1855) i Augustin-Louis Cauchy (1789–1857). Jednak przynajmniej do końca XIX wieku liczby zespolone były ciekawostką matematyczną. I właśnie dlatego, że wcześniej nie znajdowano dla „dziwnych liczb” żadnego praktycznego zastosowania, w matematyce utrwaliła się wprowadzona przez Kartezjusza zupełnie myląca nazwa liczby urojone. Wprawdzie dziś mówimy o liczbach zespolonych, ale po pierwsze, fatalne określenie nadal pokutuje w nazwie „oś urojona”. Po drugie, jedna z popularnych definicji liczby zespolonej mówi, że jest to uporządkowana para liczb rzeczywistych, a potem jedną z tych liczb nazywa się częścią urojoną liczby rzeczywistej.

Tymczasem do zapisu i obliczeń jak najprawdziwszej oporności, czyli impedancji, potrzebne są najprawdziwsze liczby, a nie jakieś urojone. I właśnie liczby zespolone nie są żadnym urojonym dziwactwem. I żadnym urojeniem nie jest wchodzący tam w grę pierwiastek z minus jeden.

Owszem, ponieważ właściwości reaktancji są specyficzne, także używane do jej opisu liczby są specyficzne, można powiedzieć – „liczby nieco bardziej skomplikowane”. Jednak wszystko jest tam prawdziwe, realne, uporządkowane, logiczne, spójne i harmonijne. Zanim poznasz kilka sposobów precyzyjnego zapisu impedancji, czyli oporności zespolonej, zajmijmy się łatwiejszymi przypadkami.

Przypadek szczególny – reaktancja

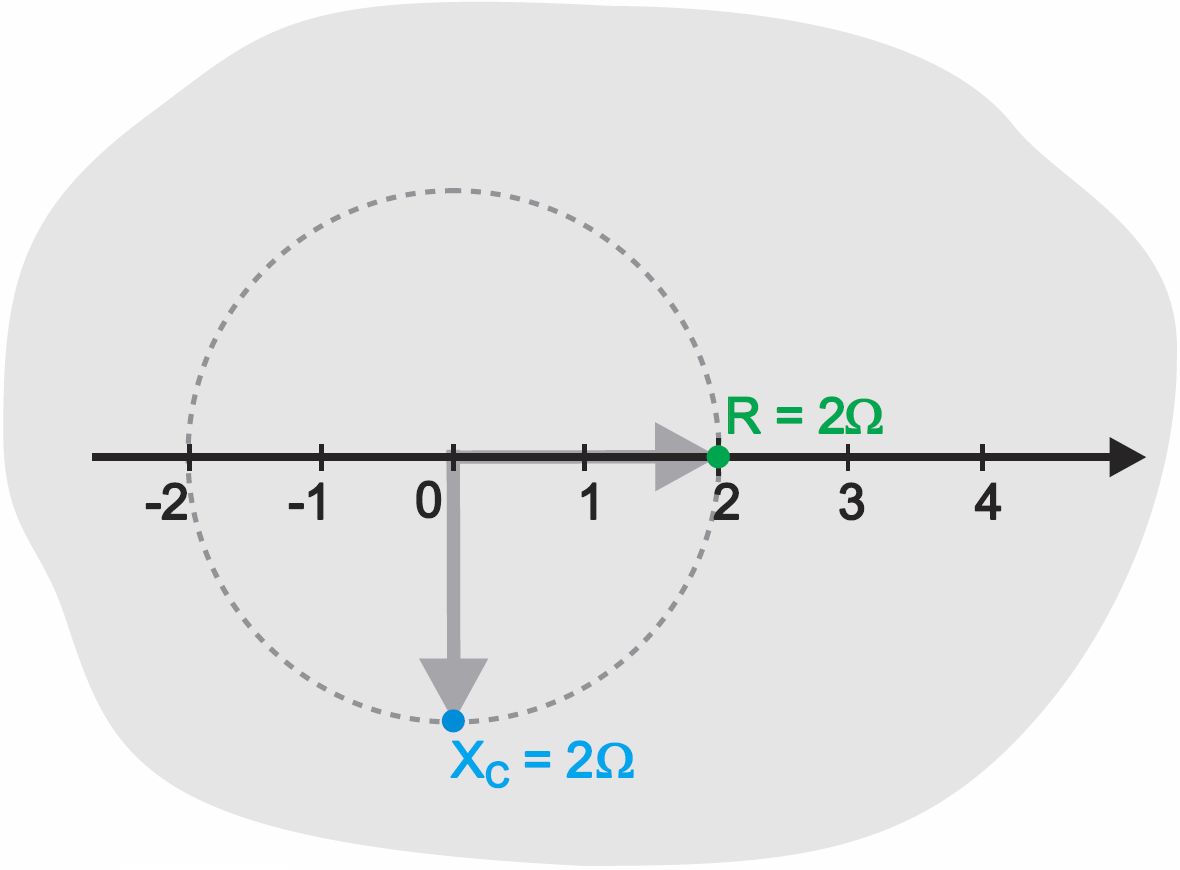
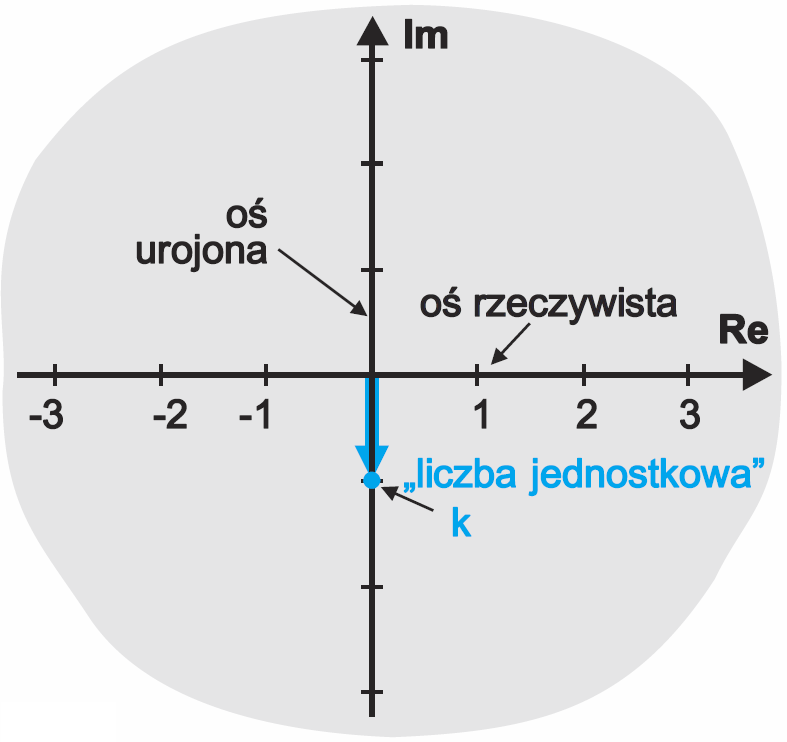
Wróćmy do rezystancji R i reaktancji kondensatora X_c, które są przypadkami szczególnymi. W przypadku rezystancji nie ma problemu, bo rezystancję wyrażoną w omach określa najzwyklejsza liczba rzeczywista, którą możemy bez trudu zaznaczyć na osi liczb rzeczywistych. Natomiast w liczbowym wyrażeniu reaktancji X_c, obok wartości podanej w omach, trzeba też zawrzeć informację o przesunięciu fazy o 90 stopni. Zgodnie z informacjami z poprzednich odcinków, w szczególności rysunku 7 (zamieszczonego w poprzednim wykładzie), moglibyśmy zaznaczyć wartość rezystancji R1 = 2 Ω oraz X_c = 2 Ω na płaszczyźnie liczbowej z rysunku 1.

Tylko nasuwa się ważne pytanie: jak zapisać wartość X_c w postaci liczbowej? I jak przeprowadzać obliczenia?

Czy może sensowny byłby zapis w rodzaju 2 Ω_(−90°)?

Jak się dalej okaże, to wcale nie jest głupi pomysł, ale może nasunął Ci się wniosek, że do pełnego scharakteryzowania reaktancji X_c obok jej wartości wystarczy podać „jednobitową” informację wskazującą, że chodzi właśnie o reaktancję pojemnościową.

Bardzo słusznie!

Właśnie w tym szczególnym przypadku „czystej reaktancji” X_c sprawa jest prosta o tyle, że kąt przesunięcia zawsze wynosi dokładnie 90 stopni, więc rzeczywiście mogłoby to być coś w rodzaju „dodatkowej jednobitowej informacji o przesunięciu”.

Chodzi nam więc o coś podobnego, jak znak minus. Otóż jeśli mamy dowolną liczbę dodatnią, to stawiając przed nią znak minus, otrzymujemy liczbę ujemną. A tak naprawdę, znak minus to w sumie to samo, co „liczba jednostkowa” minus jeden:

–1234,5 = -1 × 1234,5

Pamiętaj też, że przyzwyczailiśmy się pomijać znak plus i że można napisać:

1234,5 = +1234,5 = +1 × 1234,5

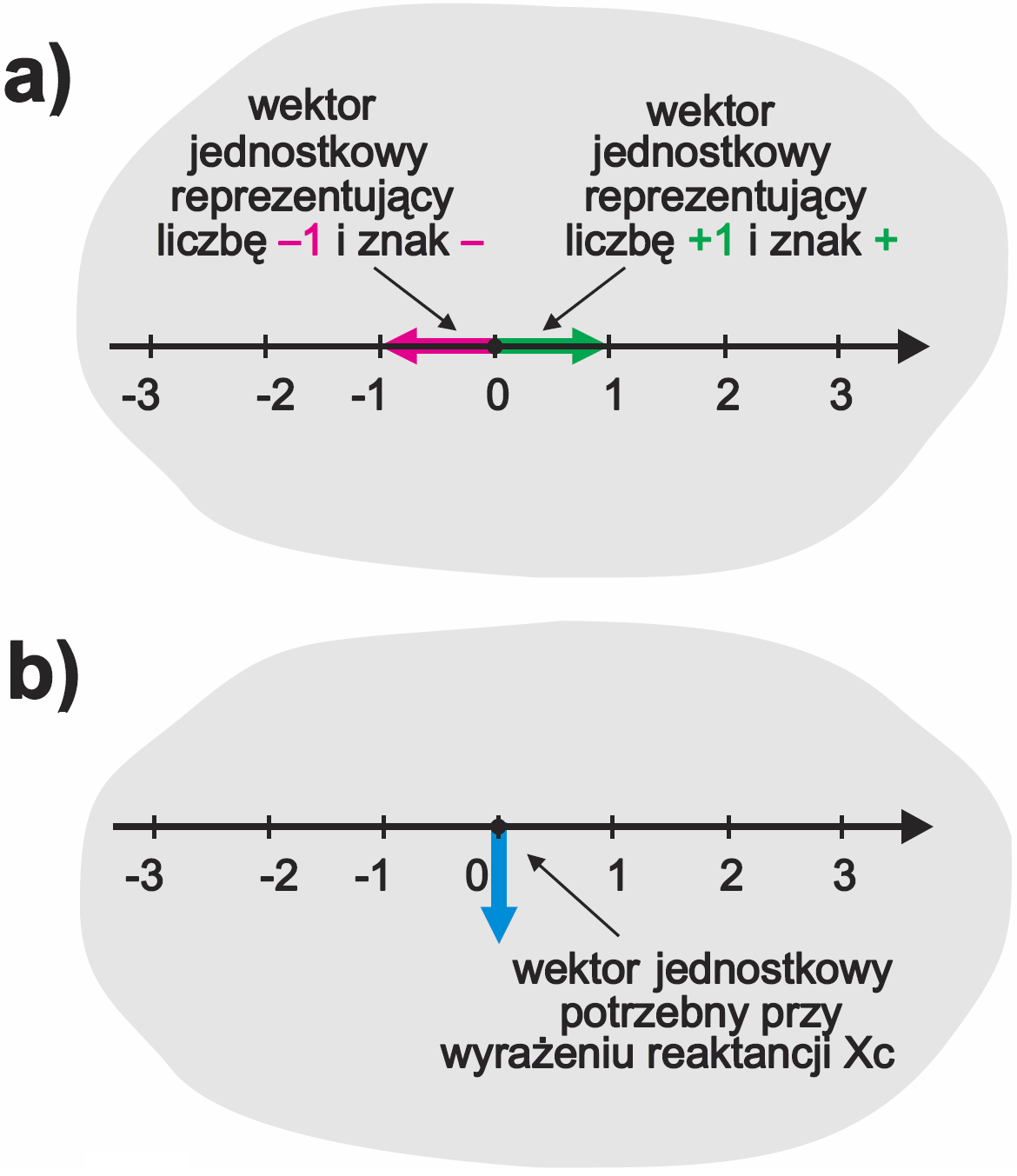
Chyba nie zaprotestujesz, jeśli powiem, że -1 i +1 są jednostkami, inaczej wektorami jednostkowymi, które też wskazują w zapisie graficznym zwrot wektora reprezentującego liczbę rzeczywistą. Ilustruje to rysunek 2a.

Teraz dla reaktancji X_c poszukujemy czegoś takiego, co postawione przed liczbą wyrażającą wartość reaktancji, wskazywałoby na przesunięcie fazowe między prądem a napięciem równe 90 stopni (π/2 radianów). Co byś powiedział na następujący zapis:

X_c = k × 2 Ω

Wtedy reaktancję obliczalibyśmy ze wzoru:

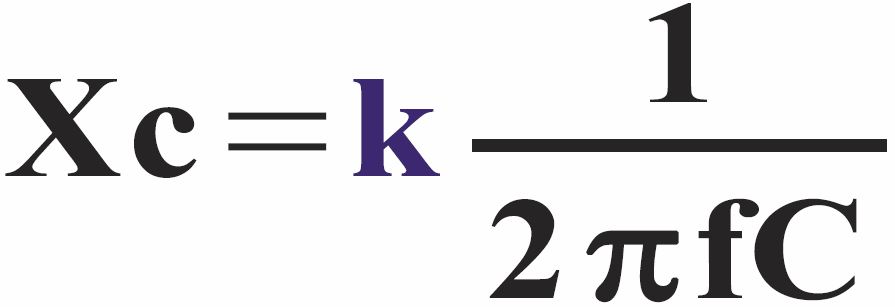
Na zasadzie analogii z rysunkiem 2a przypuszczamy, że ten czynnik k powinien być reprezentowany przez „wektor jednostkowy” skierowany w dół, jak pokazuje rysunek 2b. To nie powinno budzić Twoich wątpliwości.

A teraz kolejny bardzo ważny szczegół.

Połowa znaku minus?

Zwróć uwagę, że znak minus, czyli inaczej pomnożenie przez jednostkę -1, w reprezentacji graficznej oznacza obrót wektora (wskazu) o kąt 180 stopni.

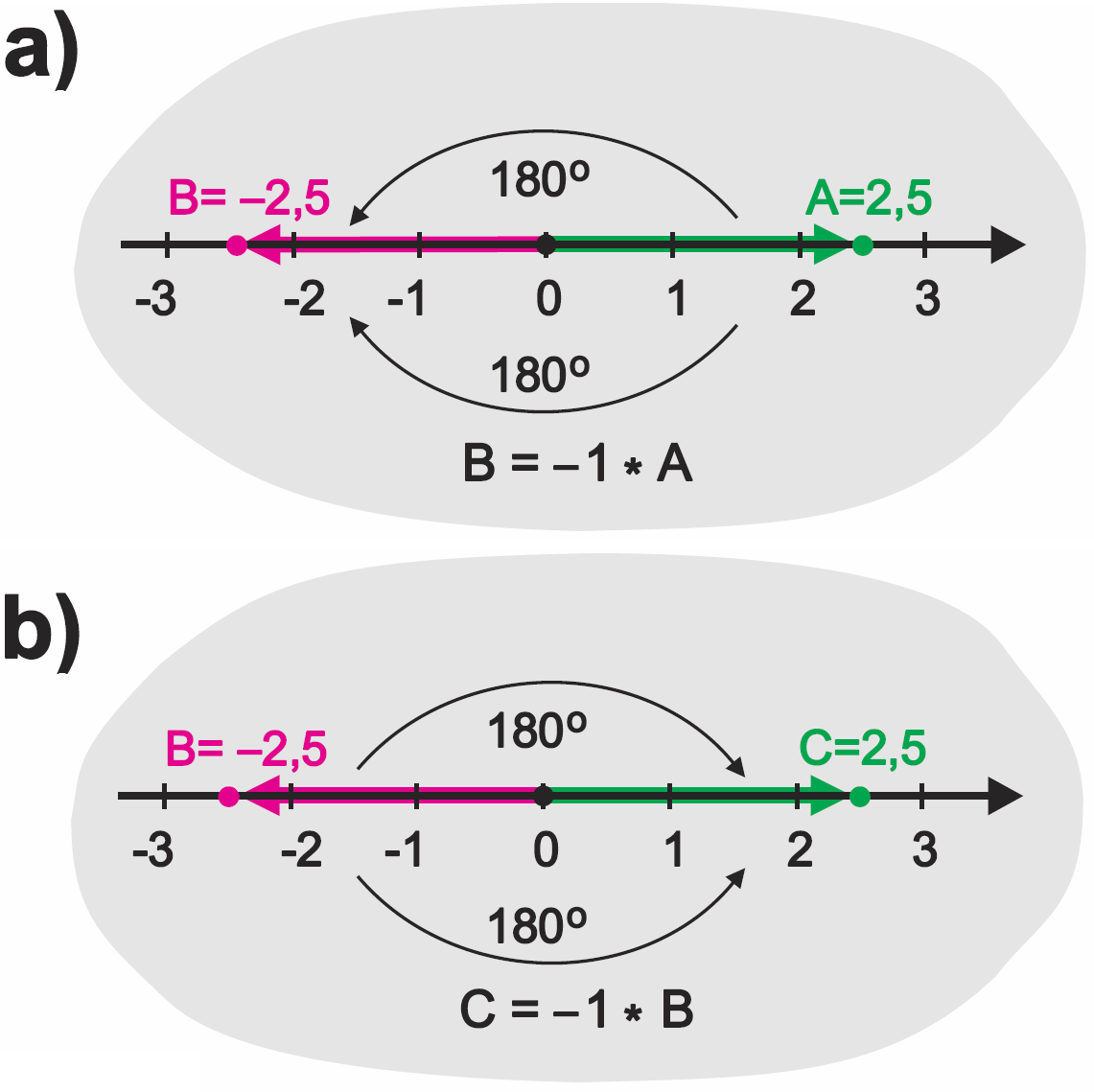
To oczywiste, że dla liczby A = 2,5 mamy:

B = -1 × A           B = -1 × 2,5 = -2,5

Ilustruje to rysunek 3a. Pomnożenie jeszcze raz przez -1 oznacza obrót o kolejne 180 stopni C = -1 × -2,5 = 2,5 – patrz rysunek 3b. Czyli znak minus niewątpliwie ma związek z obrotem o kąt 180 stopni.

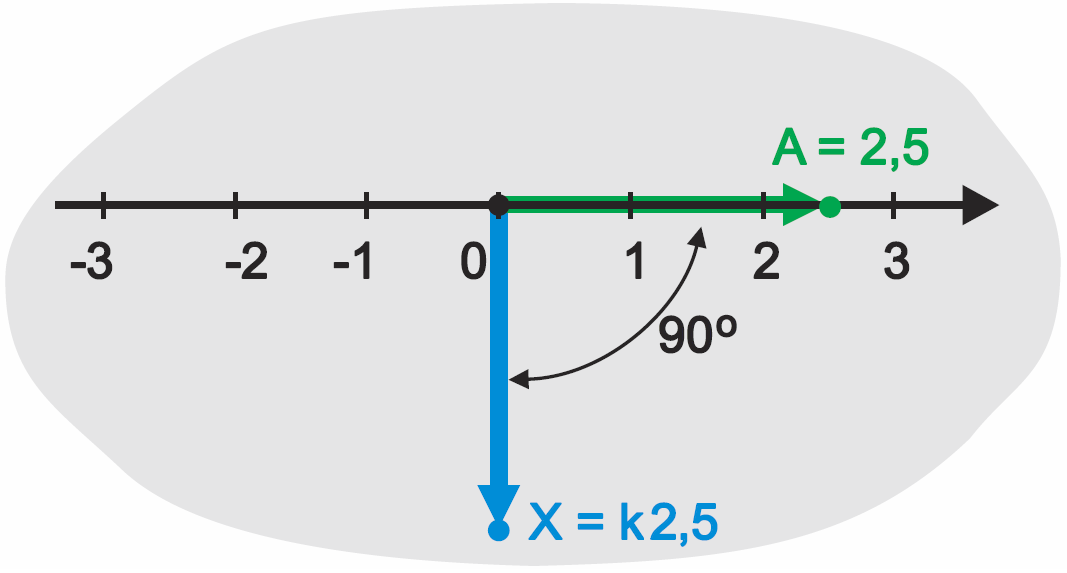
Na zasadzie analogii domyślamy się, że postawienie przed „zwykłą” liczbą znaku k (mnożenie przez jednostkę k) powinno oznaczać obrót o 90 stopni! I tak jest!

Dla liczby A = 2,5           X = k × A           X = k × 2,5 = k2,5 co zilustrowane jest na rysunku 4.

A teraz skoncentruj się: jeżeli -1 oznacza obrót o 180 stopni, a k o 90 stopni, to k jest niejako… „połową znaku minus”.

Nie bardzo mieści Ci się to w głowie, prawda? Nic dziwnego, ale czytaj dalej.

Czym więc tak naprawdę jest k? Domyślamy się, że jest to coś w rodzaju znaku plus i minus… Coś w rodzaju jednostki… Jak to jednak rozumieć, jak zapisać matematycznie i jak przeprowadzać obliczenia?

Spróbujmy to jakoś zgłębić. Wykorzystamy oczywistą zależność matematyczną: (-1)(-1) = (-1)²= +1 = 1

Otóż zgodnie z rysunkiem 3, pomnożenie przez -1 to obrót o 180 stopni.

Dwukrotnie mnożenie przez -1 zapisujemy: C = (-1)(-1) × 2,5          C = (-1)² × 2,5           C = +1 × 2,5           C = 2,5

Zwróć też uwagę, że pomnożenie przez jednostkę +1 to obrót o kąt zero stopni, co jednocześnie oznacza też obrót o 360 stopni. Przedstawmy to w tabelce:

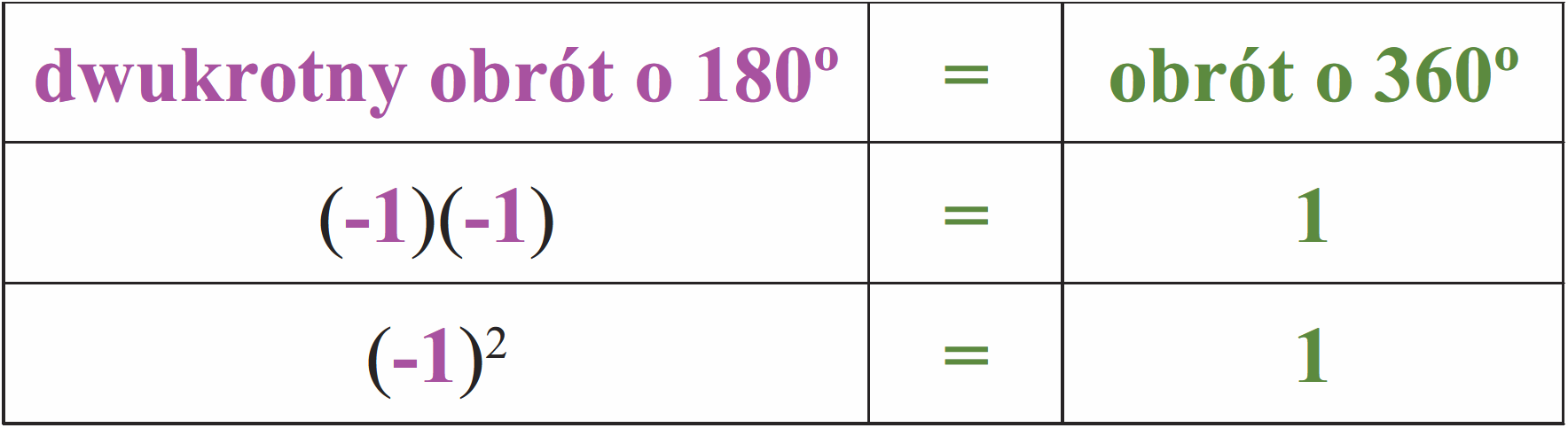
Idźmy dalej tym tropem. Nie ulega wątpliwości, że poszukiwany przez nas znak, czy raczej jednostka k, ma związek z obrotem o 90 stopni. A jeśli tak, to możemy przedstawić to w analogicznej tabelce:

Do takiej interpretacji i reprezentacji graficznej chyba nie masz zastrzeżeń.

Jednak dosłownie przerażenie może wzbudzić wniosek z dolnej kolumny, a mianowicie równość: (k)² = -1

Oto doszliśmy bowiem do słynnego pierwiastka z minus jeden. Jeśli bowiem liczba k podniesiona do kwadratu ma dać minus jeden, to natychmiast pojawia się wniosek, że k to pierwiastek z minus jeden. I momentalnie pojawia się kolejna myśl: pierwiastek z minus jeden nie istnieje…

Bez paniki! Już w poprzednim odcinku zastanawialiśmy się, co to znaczy, że liczba istnieje. W potocznym rozumieniu liczba istnieje, jeśli znajdujemy dla niej zastosowanie. Odrobinę bardziej logiczny wniosek brzmi: liczba istnieje, jeśli wraz z innymi liczbami i działaniami na nich tworzy harmonijny system. I właśnie tak jest z poszukiwaną przez nas „liczbą jednostkową” k. Na razie wiemy tylko, że k ma ścisły związek z obrotem reprezentacji graficznej liczby o 90 stopni. Wiemy, że liczba jednostkowa k ma precyzyjną reprezentację na płaszczyźnie „dziwnych liczb”. Zgodnie z wcześniejszymi rozważaniami dotyczącymi reaktancji kondensatora (X_c = k 1 / 2πfC), fazy i liczb, poszukiwana liczba k jest reprezentowana przez wektor (wskaz) jednostkowy, skierowany w dół, pokazany na rysunku 5.

Nie zdziwisz się chyba, że na płaszczyźnie „dziwnych liczb” dodaliśmy drugą oś, prostopadłą do osi liczb rzeczywistych. Właśnie tę oś, z uwagi na zaszłości historyczne, do dziś bardzo niefortunnie nazywa się osią urojoną i oznacza Im (imaginary axis), w przeciwieństwie do osi poziomej, nazywanej osią rzeczywistą lub osią liczb rzeczywistych, oznaczaną Re (real axis). Teraz już większego sensu nabiera zapis reaktancji z rysunku 1 w postaci X_c = k × 2 Ω. Ale co znaczy, że liczba k podniesiona do kwadratu daje -1?

Pierwiastki z minus jeden…

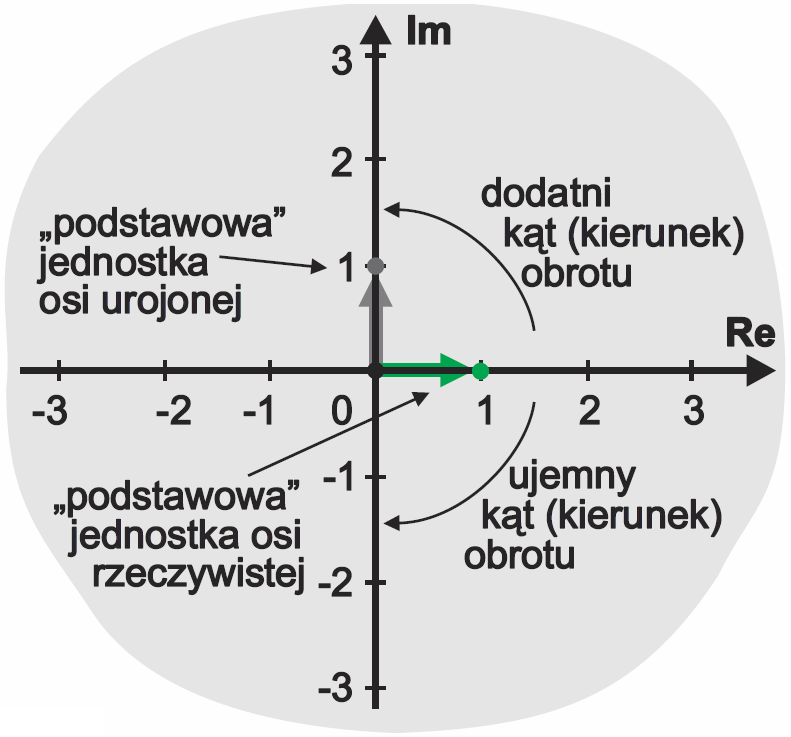
W matematyce przyjęto, że dodatni zwrot osi liczbowej skierowany jest w prawo. Podobnie przyjęto, że dodatni zwrot dodanej na rysunku 5 pionowej osi urojonej powinien być skierowany do góry. Oznacza to, że w matematyce „podstawowa” jednostka tej nowej osi urojonej jest wektorem jednostkowym skierowanym do góry. Ponadto w matematyce przyjęto, że dodatni kierunek obrotu jest przeciwny do ruchu wskazówek zegara. Pokazuje to rysunek 6.

Tymczasem nasz wektor jednostkowy k z rysunku 5 jest skierowany w dół, a jeśli chodzi o obrót o kąt 90 stopni, jest to obrót zgodnie z ruchem wskazówek zegara, czyli w matematycznym kierunku ujemnym. Czy tu jest jakaś sprzeczność? Nie! Wróćmy do wcześniejszych dwóch małych tabelek.

W dolnym wierszu pierwszej z nich mamy zapis: (-1)²= 1 będący rozwiązaniem równania (a)² = 1

Czy jednak, patrząc na ogólne równanie (a)² = 1, powiemy, że a = -1?

Chyba nie. Większość z nas powie raczej w pierwszym momencie, że jeśli (a)² = 1, to a = 1.

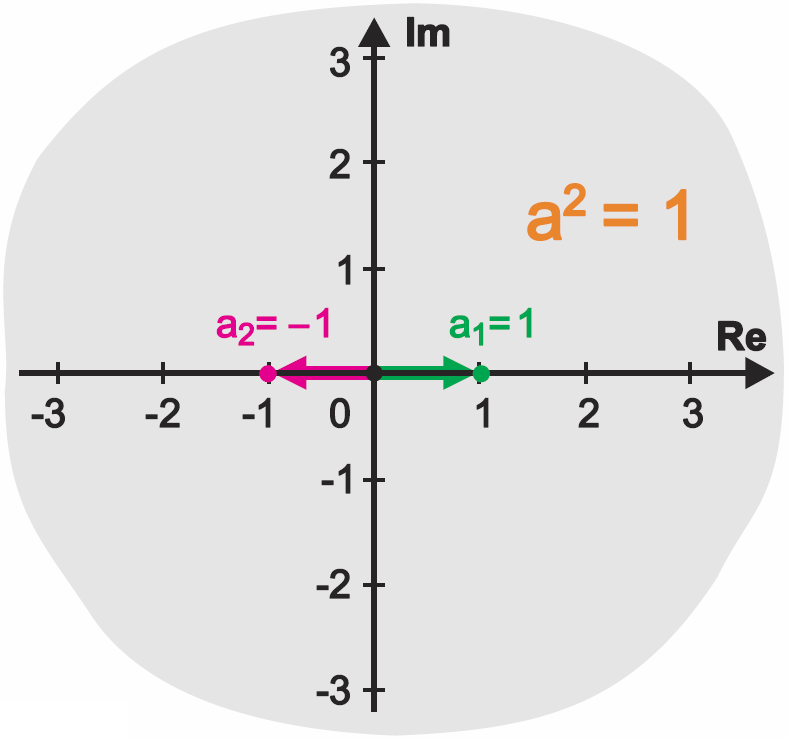
Dopiero po chwili zastanowienia powiemy, że równanie (a)²= 1 ma dwa rozwiązania: a = 1           a = -1

I oba te rozwiązania reprezentowane są przez dwa przeciwnie skierowane wektory jednostkowe, jak pokazuje rysunek 7.

Analogicznie w dolnym wierszu drugiej tabelki mamy: (k)² = -1

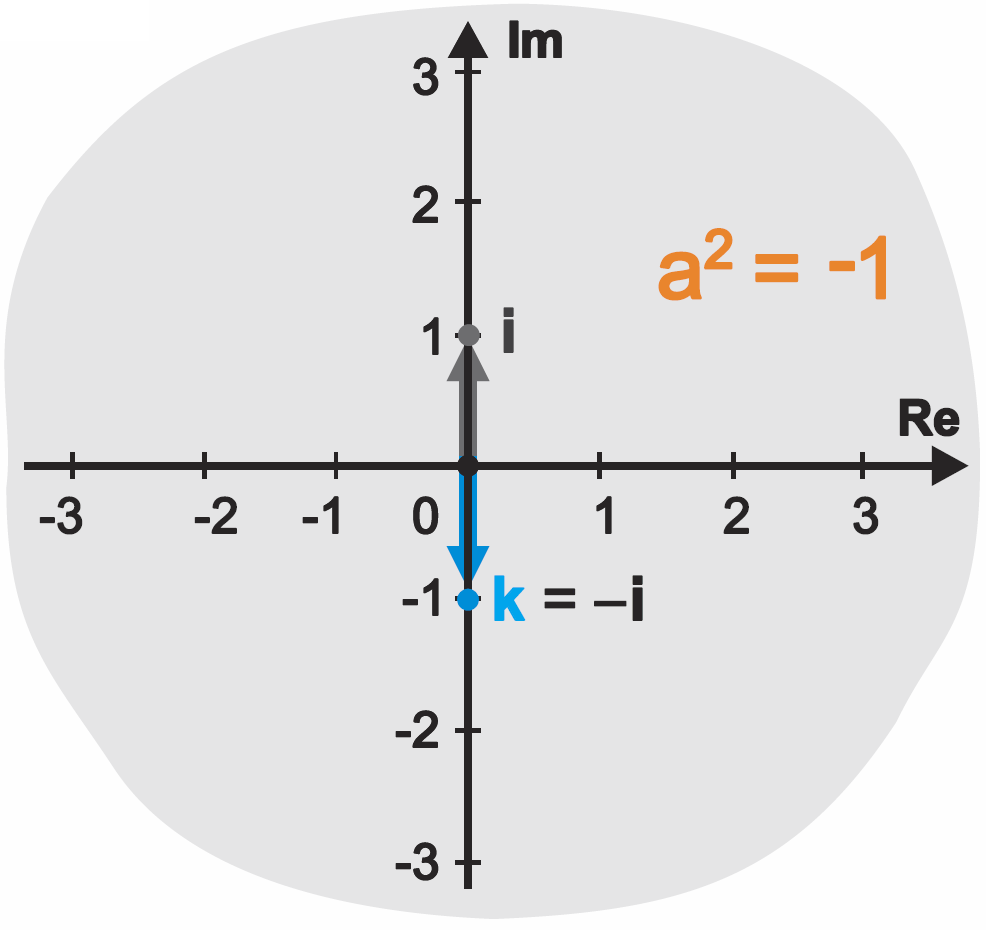
I tak samo równanie (k)² = -1 ma dwa rozwiązania. Analogicznie jak na rysunku 7, rozwiązania te są reprezentowane przez dwa wektory jednostkowe na osi pionowej, Poszukiwana przez nas do celów jak najbardziej praktycznych „ujemna” jednostka k jest reprezentowana przez wektor jednostkowy skierowany w dół. Natomiast „dodatnia” jednostka na pionowej osi jest skierowana do góry. Od dawna ta „dodatnia”jednostka oznaczana jest w matematyce małą literką i.

A jeśli tak, to k = -i. Ilustruje to rysunek 8.

I oto doszliśmy do bardzo ważnego momentu: i jest „podstawową” jednostką pionowej osi. Co ciekawe, jednostka i także reprezentuje obrót o 90 stopni i także dla niej prawdziwa jest zależność: (i)² = -1 Wcześniej ustaliliśmy, że (k)² = -1

Jeszcze raz pytamy, czy nie ma tu sprzeczności?

Absolutnie nie! Właśnie reprezentacja graficzna pokazuje, że wszystko to ma głęboki sens. Przecież rozwiązaniem równania: x² = -1 są dwie liczby:

zarówno „liczba jednostkowa” i, jak też liczba k. Możemy się też domyślać, że liczba i reprezentuje obrót o 90 stopni w matematycznym kierunku dodatnim, czyli przeciwnie do ruchu wskazówek zegara, a liczba k – w kierunku ujemnym, zgodnie ze wskazówkami zegara.

I jeszcze jeden szczegół: podnieśmy i do potęgi czwartej (i⁴). Wykorzystajmy zależności:

i² =-1 oraz (-1)² = 1           1 = (-1)² = (i²)² = i⁴

Moglibyśmy wysnuć zaskakujący wniosek, że… i jest pierwiastkiem czwartego stopnia z jedynki. Ale w to się nie wgłębiajmy. Zauważ jedynie, że: k = i

A teraz jeszcze jeden szczegół dla zaawansowanych i dociekliwych: być może byłbyś skłonny zapisać co następuje:

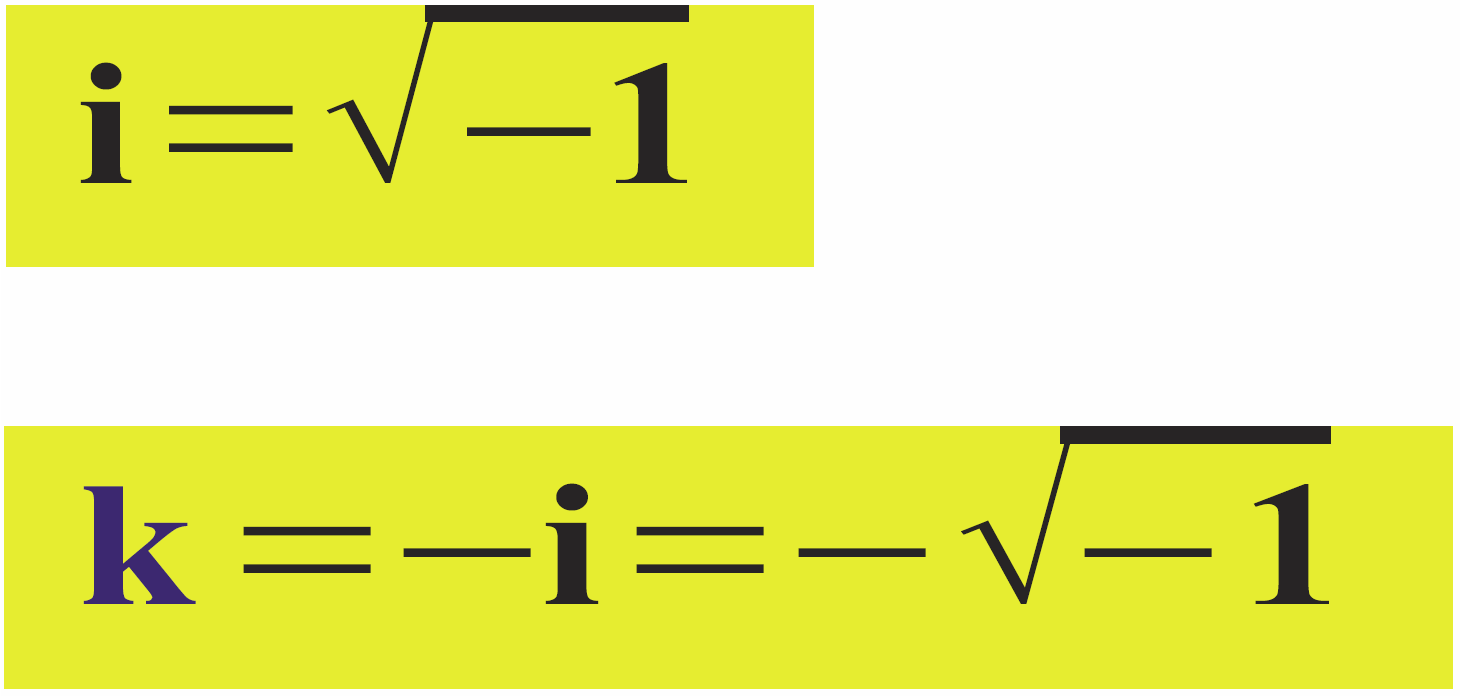
Coś w tym jest, jednak jest tu pewna nieścisłość, bo zakładamy, że i to pierwiastek z minus jeden. Tymczasem, zgodnie z definicją, pierwiastek stopnia n z liczby a to taka liczba x, która podniesiona do potęgi n, daje liczbę a                     (xⁿ = a).

W naszym przypadku powiemy, że pierwiastkiem kwadratowym z liczby -1 jest taka liczba, która podniesiona do kwadratu da właśnie –1. Przed chwilą stwierdziliśmy, że są dwie takie liczby, czyli istnieją dwa pierwiastki z minus jeden. Pierwiastkiem z minus jeden jest zarówno liczba i, jak też liczba k. Podobnie, jak istnieją dwa pierwiastki kwadratowe z liczby +1: jednym jest liczba +1, drugim –1.

„Dziwna jedynka”

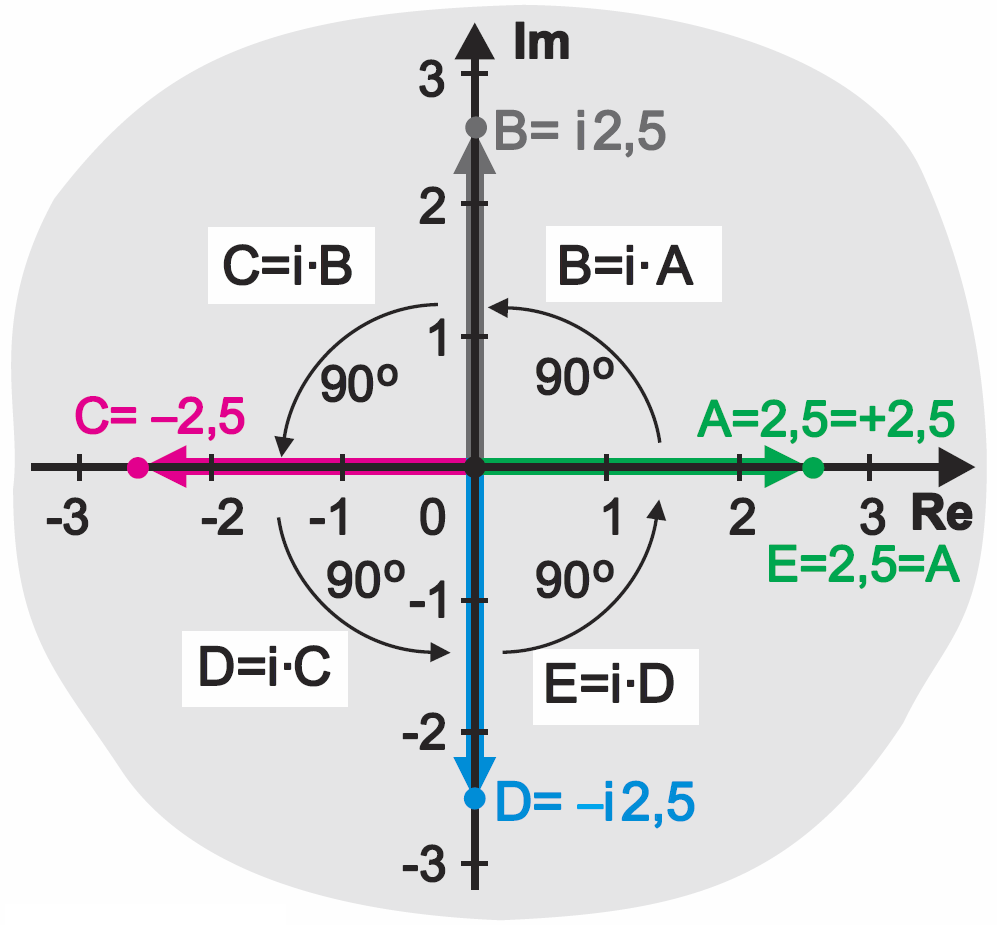
Nie przyzwyczajaj się więc do dość powszechnego sformułowania, że i to pierwiastek z minus jeden. Raczej traktuj i jako rodzaj „bardzo dziwnej jedynki” lub nawet jako „połowę znaku minus”. Wcześniej doszliśmy do wniosku, że -1 też jest „dziwną jedynką”, ponieważ pomnożenie liczby przez -1 powoduje obrót jej reprezentacji graficznej o 180 stopni (rysunek 3). Teraz i okazuje się „jeszcze dziwniejszą jedynką”, ponieważ pomnożenie przez i powoduje obrót graficznej reprezentacji liczby o 90 stopni. Weźmy na przykład „zwyczajną” liczbę A = 2,5. Pomnożenie jej przez i daje:

B = i × A = i × 2,5 = i2,5

Mnożymy jeszcze raz przez i: C = i × B = i × i × 2,5 = i² × 2,5 = -1 × 2,5 = -2,5

Jeszcze raz: D = i × C= i × i² × 2,5 = i³ × 2,5 = i × -1 × 2,5 = -i2,5

i jeszcze raz: E = i × D = = i × i³ × 2,5 = i⁴ × 2,5 = 1 × 2,5 = 2,5

Co jest zilustrowane na rysunku 9. Jeszcze raz powtarzam: nie próbuj sobie wyobrażać, że i to pierwiastek z minus jeden, tylko że jest to „bardzo dziwna jedynka” i rodzaj znaku, takiego jak minus i plus, reprezentujący obrót o 90 stopni w „matematycznym” kierunku dodatnim.

Wróćmy też do naszej liczby k = -i, którą tymczasowo wprowadziliśmy tylko w związku z reaktancją pojemnościową. Teraz już masz komplet informacji o precyzyjnym sposobie matematycznego zapisu reaktancji. Pamiętając, że k = -i napiszemy:

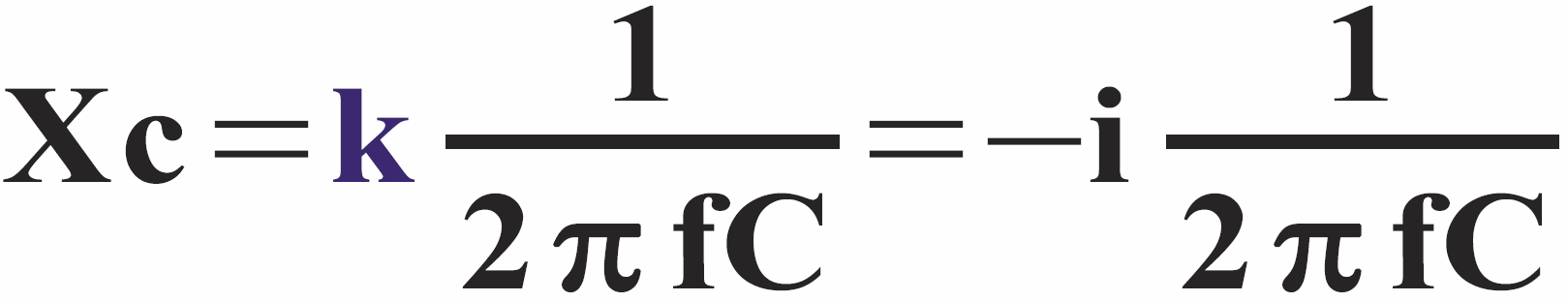
Moglibyśmy teraz jak najbardziej ściśle zapisać, że reaktancja kondensatora z rysunku 1 wynosi X_c= –i2 Ω

Jednak w elektronice literka i kojarzy się z prądem. Niewątpliwie mogłoby dojść do różnych pomyłek. Dlatego my, elektronicy, na określenie „bardzo dziwnej jedynki”, zamiast literki i stosujemy literkę j. Piszemy:

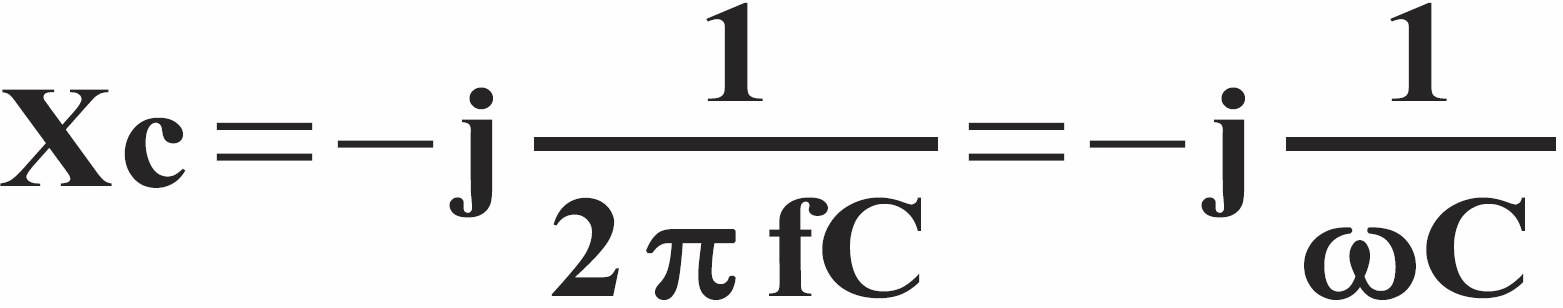
gdzie małą literą omega oznaczamy tzw. pulsację ω = 2πf. Choć nie zajmowaliśmy się jeszcze cewkami, dodam, że w cewce (w indukcyjności) też występuje przesunięcie między prądem a napięciem i też wynosi ono 90 stopni. W kondensatorze napięcie opóźnia się względem prądu, a w cewce odwrotnie – prąd opóźnia się względem napięcia. Przesunięcie fazy też wynosi 90 stopni, ale w matematycznym kierunku dodatnim. A oto ścisły wzór na reaktancję indukcyjną cewki:

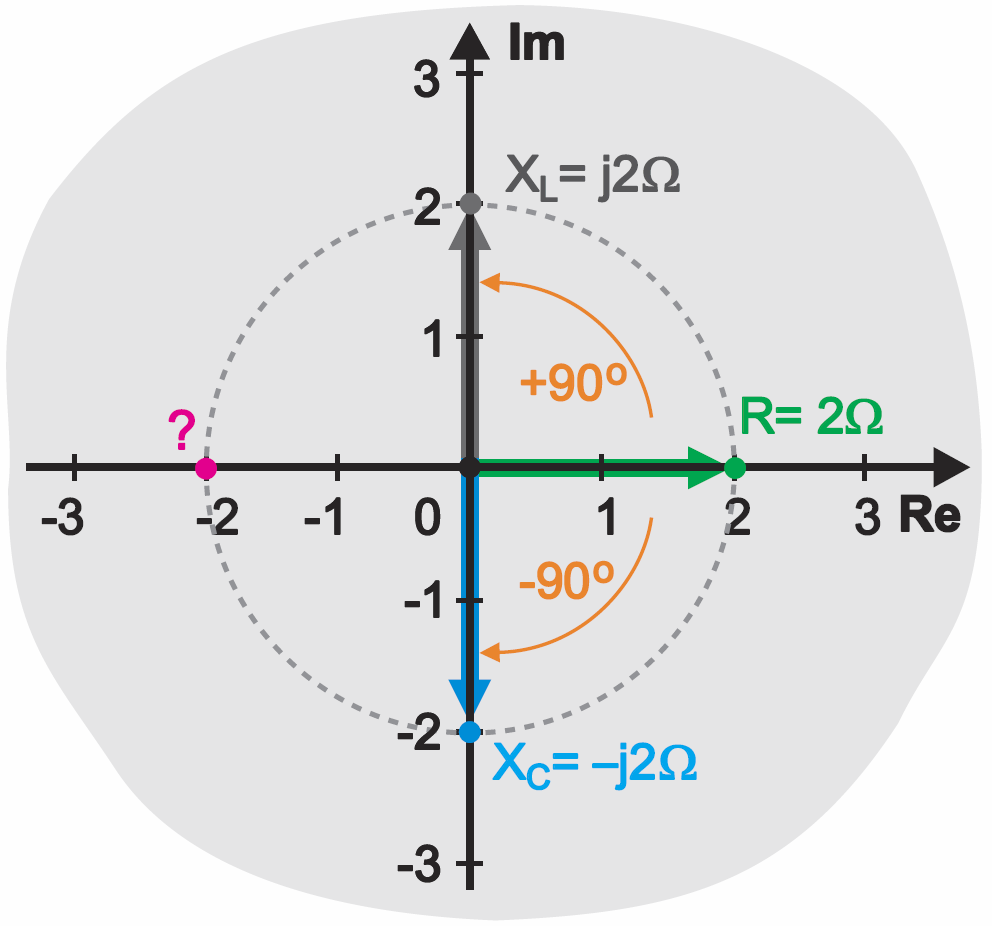
Jeśli mamy rezystancję R = 2 Ω, reaktancję pojemnościową X_c = 2 Ω, a ściślej X_c = –j2 Ω, reaktancję indukcyjną X_L = 2 Ω, ściślej X_L = j2 Ω, możemy je z pełnym zrozumieniem opisać matematycznie oraz przedstawić graficznie na rysunku 10. Nie dziw się też, jeśli mówimy, że przesunięcie fazy w kondensatorze jest ujemne, a w cewce – dodatnie.

I oto mamy „rozgryzione” trzy przypadki szczególne: rezystancję, reaktancję pojemnościową i indukcyjną. Być może jesteś ciekaw czwartego przypadku szczególnego – oporności, której reprezentacja leżałoby na ujemnej części osi liczb rzeczywistych. Wygląda, że byłaby to ujemna rezystancja. I takowa istnieje – jest zresztą wykorzystywana w praktyce. Na razie, nie ma jednak pojedynczego elementu, dwukońcówkowego „ujemnego rezystora ” , natomiast niektóre układy elektroniczne zachowują się jak ujemna rezystancja , jednak nie będę Ci mącił w głowie tą kwestią. Nas bardziej od omówionych właśnie przypadków szczególnych interesują powszechnie spotykane „ przypadki pośrednie” i kwestia: jak zapisać liczbowo dowolną oporność wypadkową, impedancję Z, która na przykład jest złożeniem rezystancji i reaktancji pojemnościowej. Tymi sprawami zajmiemy się w następnym odcinku.

Piotr Górecki