Elektronika (nie tylko) dla informatyków (11) Tajemnice liczb zespolonych

W poprzednim odcinku zajmowaliśmy się sposobami matematycznego zapisu wartości rezystancji R, reaktancji pojemnościowej X_C oraz reaktancji indukcyjnej X_L. To były przypadki szczególne, które pozwoliły zrozumieć sens stosowanej w elektronice liczby j (która w matematyce oznaczana jest i). Liczba j (i) okazała się „dziwną jednostką”, „dziwną jedynką” czymś w rodzaju „połowy znaku minus”. Teraz zajmiemy się przypadkami pośrednimi, czyli impedancją Z.

Zastanówmy się, jak zapisać liczbowo dowolną oporność wypadkową, czyli impedancję Z, która może być dowolnym złożeniem R, X_C oraz X_L? I jak przeprowadzać obliczenia?

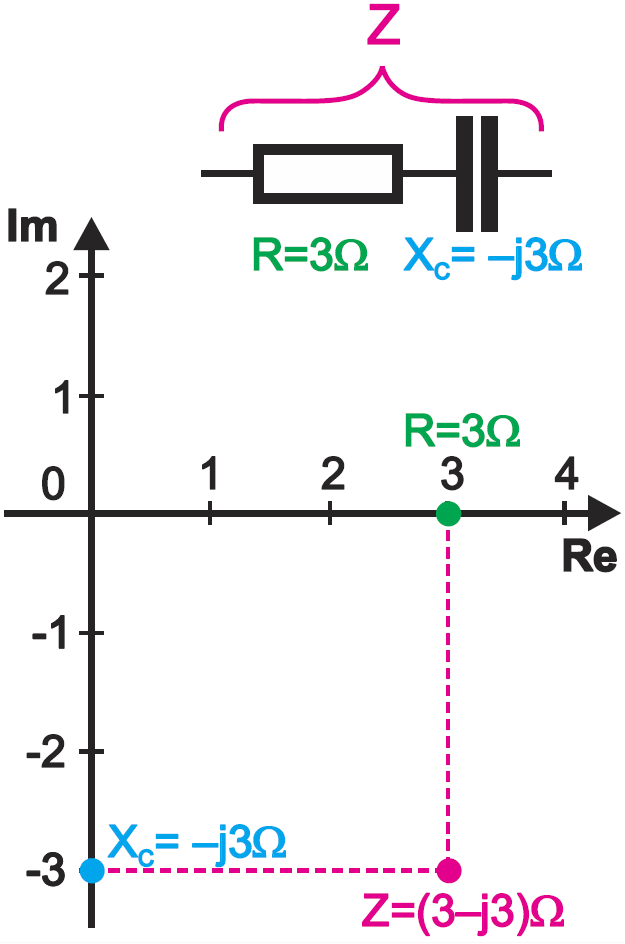
Wiesz z poprzednich odcinków, że przy połączeniu szeregowym impedancja Z jest wektorową sumą R i X_C:

Z = R –jX_C = R –j(1/2πfC)

Łatwo to zrozumieć, policzyć i wynik przedstawić graficznie. Załóżmy, że R = 3 Ω, X_C = –j3 Ω. Na rysunku 1 zaznaczyłem wartość impedancji Z. Przy połączeniu szeregowym po prostu sumujemy oporność składników. Co więc powiesz na zapis: Z = (3–j3) Ω?

Mam nadzieję, że bez trudu zaakceptujesz taki intuicyjny zapis liczb zespolonych. Tylko czy 3–j3 to jedna liczba, czy złożenie dwóch liczb?

Wielokrotnie podkreślałem, że reaktancje X_C, X_L i impedancję Z chcemy wyrazić jedną „dziwną” liczbą, która jednocześnie określa i wartość w omach, i przesuniecie fazy. Liczba ta jest reprezentowana przez jeden punkt płaszczyzny liczbowej. Właśnie 3–j3 to jedna liczba – liczba zespolona, niosąca informację zarówno o wartości impedancji, jak i o kącie przesunięcia między napięciem a prądem. Zapisaliśmy tę liczbę zespoloną w tak zwanej postaci algebraicznej, zwanej też kanoniczną.

Problem połączenia równoległego

W przypadku połączenia szeregowego sprawa jest oczywista i nie powinna budzić wątpliwości. Rysunek 2 pokazuje przykład, gdy liczbowa wartość R jest taka sama jak X_C. Znając wartości R i X_C łatwo zapiszemy w postaci algebraicznej liczbową wartość impedancji.

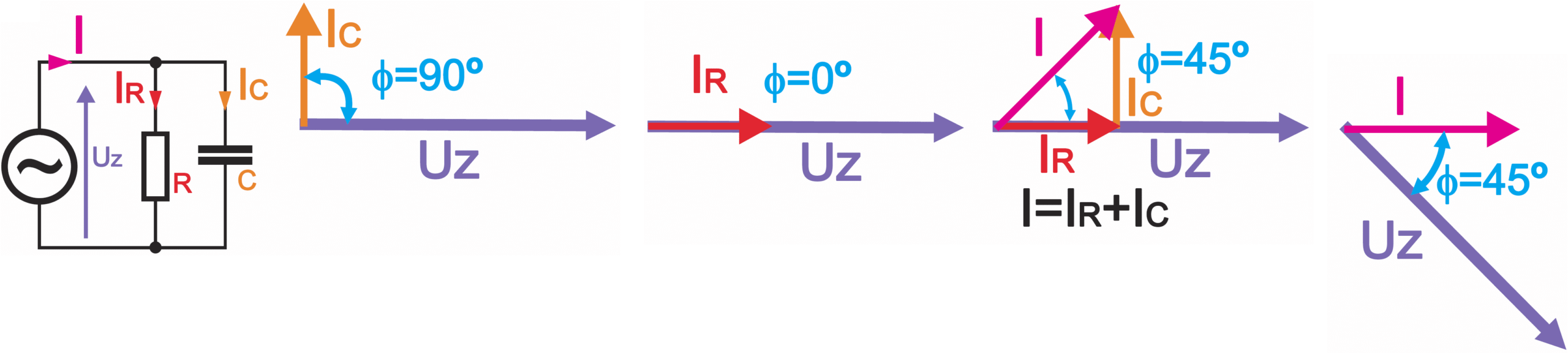
Ale jak obliczyć i przedstawić impedancję połączenia równoległego R i X_C?

Moglibyśmy zobrazować sytuację na rysunku 3. Tym razem na obu elementach występuje to samo napięcie zasilające U_Z. Trzeba obliczyć wartości prądów i dodać je wektorowo. Także i tu zależność między wektorami wypadkowego prądu i napięcia zasilającego to oporność wypadkowa – impedancja Z połączenia równoległego.

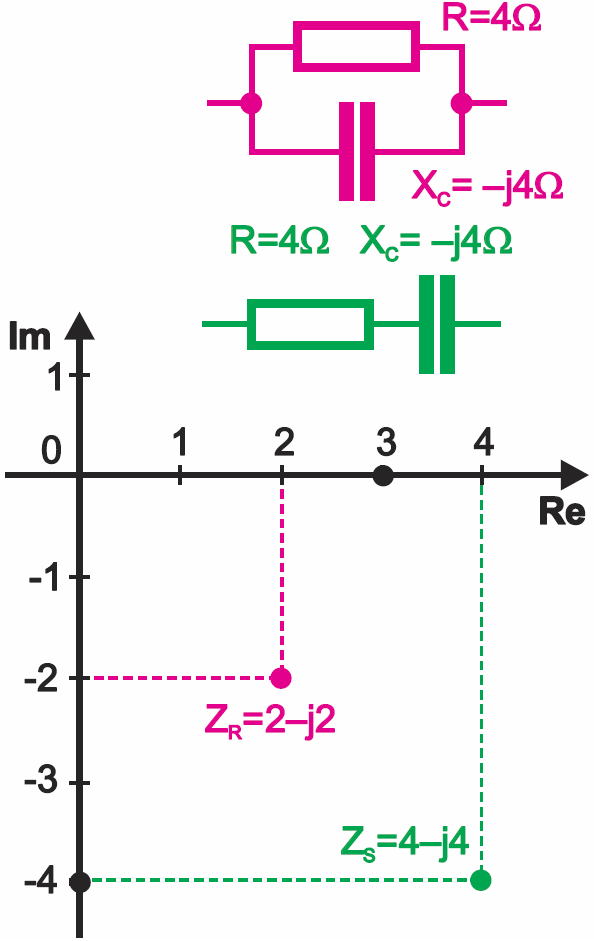
Zwróć uwagę na umieszczone po prawej stronie fragmenty rysunków 2 i 3. Są identyczne. Oznacza to, że w tym akurat przypadku impedancja połączenia szeregowego elementów R1, C1 jest dokładnie równa impedancji równoległego połączenia R2, C2. Oczywiście R1≠R2 i C1≠C2. Przecież impedancja połączenia szeregowego powinna być większa niż każdy ze składników, a połączenia równoległego – mniejsza niż każdy ze składników (nietrudno jednak się zorientować, że równość impedancji z rysunków 2, 3 nastąpi, gdy R1=0,5R2 i C1=0,5C2).

W każdym razie okazało się, że także impedancję połączenia równoległego R, C, bez problemu możemy wyrazić jako liczbę zespoloną w postaci algebraicznej.

A tak na marginesie: rysunek 4 pokazuje oporność wypadkową szeregowego i równoległego połączenia gdy R=4 Ω, X_C=–j4 Ω. W tym akurat przypadku uzyskaliśmy „okrągłą” wartość impedancji połączenia równoległego (2-j2). Ale to rzadki wyjątek.

 

W praktyce graficzny sposób obliczania impedancji połączenia równoległego okazałby się zbyt uciążliwy, wręcz nie do przyjęcia. Potrzebna jest jakaś prostsza metoda obliczeń. I znów podstawowa idea jest beznadziejnie prosta. Przypomnij sobie wzór na oporność wypadkową przy równoległym łączeniu rezystancji:

1/R_Z = 1/R1 + 1/R2 +1/R3 oraz wersję dla dwóch rezystorów R_Z = R1×R2 / (R1+R2)

Zależności te możemy śmiało wykorzystać do obliczeń przy prądach zmiennych. Oczywiście obliczenia połączenia równoległego R, X_C, X_L należy wykonać z wykorzystaniem poznanych właśnie liczb zespolonych. Okazuje się, że te zależności dotyczą zarówno prądów zmiennych, jak i stałych.

Prawdziwe są nie tylko wzory: R_Z = R×X_C / (R+X_C) czy 1/Z = 1/R + 1/X_C czy 1/Z = 1/Z₁+ 1/Z₂+ … +1Z_N

Liczby zespolone będziemy wykorzystywać w elektronice do wszelkich podobnych obliczeń, także dotyczących reaktancji indukcyjnej X_L oraz wszędzie tam, gdzie w grę wchodzi przesunięcie fazy między prądem a napięciem.

Kolejny raz widzisz jasno, dlaczego wielokrotnie podkreślałem, że reaktancje X_C, X_L i impedancję Z chcemy wyrazić jedną liczbą (zespoloną), która jednocześnie określa i wartość w omach i przesuniecie fazy. Będziemy po prostu podstawiać do wzorów i liczyć, liczyć, liczyć…

W tym celu musisz jednak przynajmniej w zarysie poznać zasady obliczeń na liczbach zespolonych, a wcześniej różne sposoby zapisu takich liczb.

Postać algebraiczna

Oczywiście graficzną reprezentacją liczby zespolonej jest pojedynczy punkt płaszczyzny. Jest jednak pewien kłopot z jej zapisaniem. Zgodnie z nazwą, liczba zespolona jest „bogatsza”, niesie „więcej informacji” niż liczba rzeczywista. Problem w tym, że nie bardzo potrafimy zapisać „w jednym kawałku” tę „bogatszą treść” liczb zespolonych. Zapewne można byłoby wymyślić jakiś niezwykły sposób zapisu liczb zespolonych „w jednym kawałku”. Jednak, co bardzo ważne, przy zapisywaniu liczb zespolonych należy zachować „kompatybilność wstecz” i nie wprowadzać rewolucji, by liczby rzeczywiste, będące podzbiorem liczb zespolonych, zapisywać tak jak dotąd.

Chciałbym tu przypomnieć, że czymś zupełnie innym jest sama liczba i jej matematyczne właściwości, a czym innym sposób jej zapisu. Liczby można zapisywać w różny, mniej lub bardziej wygodny sposób. Przykładem prostego, ale wyjątkowo niewygodnego sposobu zapisu jest system rzymski. Pozwala zapisać tylko liczby naturalne, bez zera i jest koszmarnie niewygodny do obliczeń, a właściwie w ogóle nie nadaje się do obliczeń. Nie można zapisywać w tym systemie liczb ujemnych, ułamków, a tym bardziej liczb niewymiernych, jak choćby liczby π, czy pierwiastka z dwóch. Podobnie bardzo niewygodny do obliczeń był na przykład system grecki, gdzie wartość „podstawowych” cyfr i niektórych „okrągłych” liczb przedstawiana była przez kolejne litery alfabetu (24 litery greckie plus dodatkowe trzy znaki adaptowane z alfabetów semickich). Nieporównanie wygodniejsze są pozycyjne systemy zapisu liczb. Dziś powszechnie wykorzystujemy system dziesiętny, a w informatyce także dwójkowy (binarny) i szesnastkowy (heksadecymalny).

I oto natknęliśmy się na problem z zapisem liczb zespolonych. Otóż zapisujemy je przynajmniej na trzy różne sposoby. Zgodnie z nazwą: liczby zespolone (complex numbers), często stosowany jest złożony, „dwuczłonowy” zapis w postaci algebraicznej, bezpośrednio związany z omawianą reprezentacją graficzną, w którym pierwszy człon reprezentuje część (składową) rzeczywistą ℜ, (Re) a drugi – część (składową) urojoną ℑ (Im). I właśnie 3–j3 liczba zespolona z rysunku 1, zapisana jest w postaci algebraicznej.

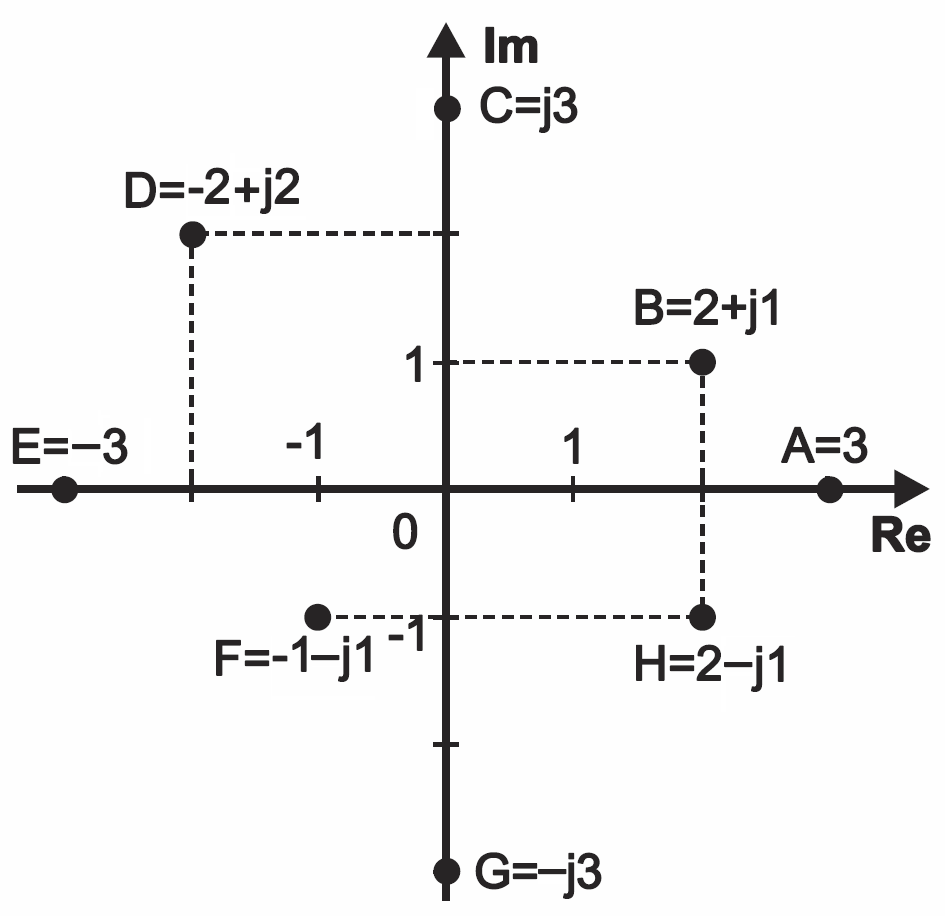
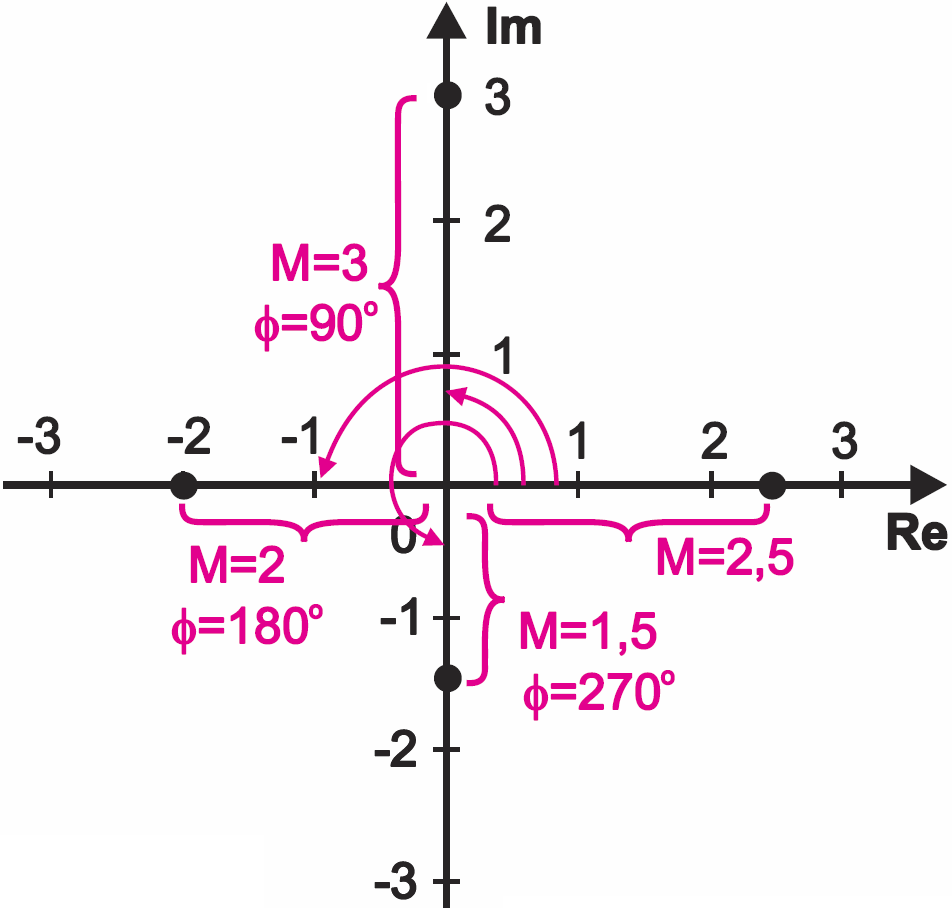
Na rysunku 5 punkt A reprezentuje „najzwyczajniejszą”, liczbę rzeczywistą 3. Punkt B ma „współrzędną poziomą” ℜ równą 2, „współrzędną pionową” ℑ równą 1. Punkt ten reprezentuje liczbę zespoloną 2+j1. Punkt C leży na osi urojonej w odległości trzech jednostek od punktu zerowego i reprezentuje liczbę j3. Współrzędne punktu D reprezentuje liczbę –2+j2. Dla kolejnych punktów napiszemy: E = –3+j0 = –3 F = –1–j1 G = 0–j3 = –j3 H = 2–j1

Zauważ, że zachowana jest w pełni kompatybilność wstecz – liczby rzeczywiste, czyli takie liczby zespolone, w których część urojona jest równa zeru, zapisujemy dokładnie tak, jak jesteśmy do tego przyzwyczajeni „od zawsze”.

Inne sposoby zapisu

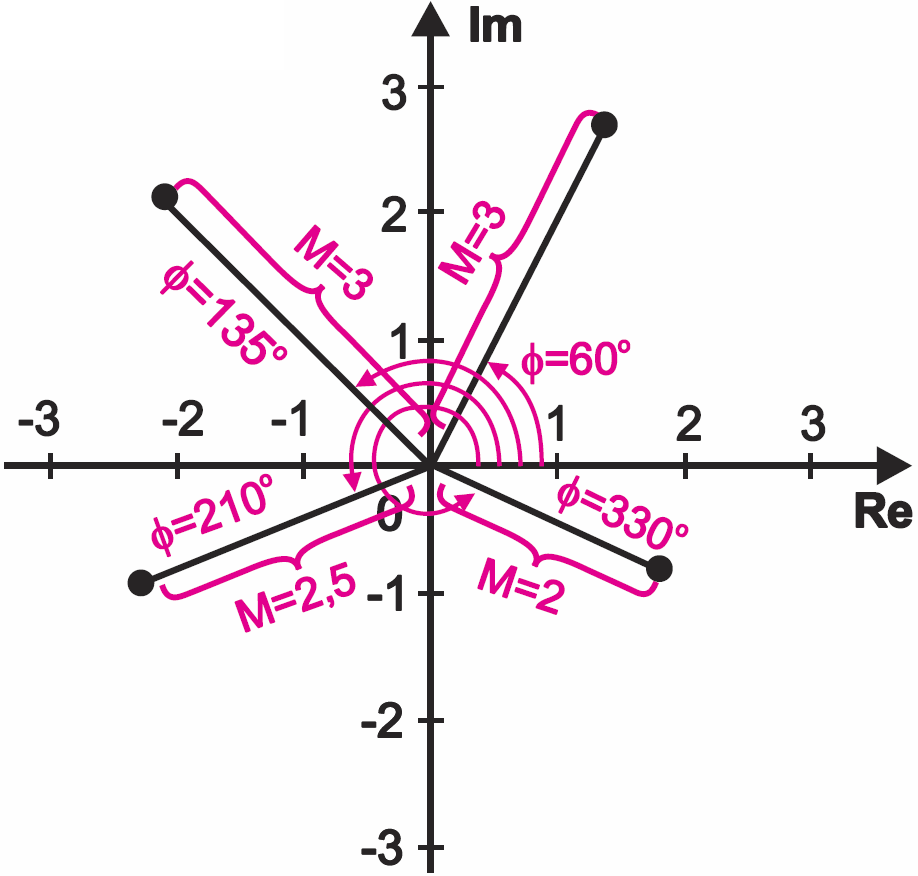
Co bardzo ważne, nie jest to jedyny sposób zapisu liczb zespolonych. Wróćmy do reprezentacji graficznej. Inny sposób zapisu polega na podaniu długości wektora (wskazu), łączącego punkt zerowy z punktem reprezentującym liczbę – to tak zwany moduł liczby zespolonej, oraz kąta (tak zwany argument) między dodatnim zwrotem osi liczb rzeczywistych i powstałym wskazem. Moduł możemy oznaczyć literką M, a argument literką φ. Na rysunku 6 masz graficzną reprezentację kilku liczb, oznaczonych w taki właśnie sposób.

Idea jest jasna, prawda? Tylko jak to sensownie zapisać?

Aby znaleźć odpowiedź, powróćmy do postaci algebraicznej. Otóż znając część rzeczywistą i urojoną możemy obliczyć zarówno moduł, jak i argument. Można wykorzystać wzór Pitagorasa i definicję tangensa kąta: tgφ=y/x, a to daje φ=arctg(y/x). Wykorzystamy wzory:

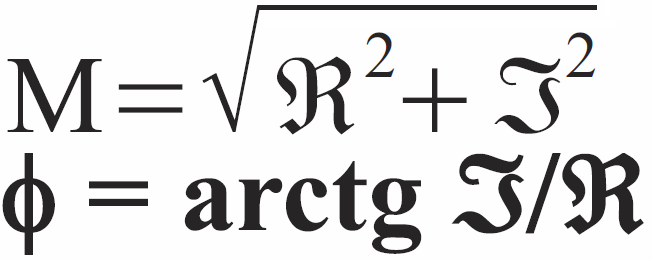
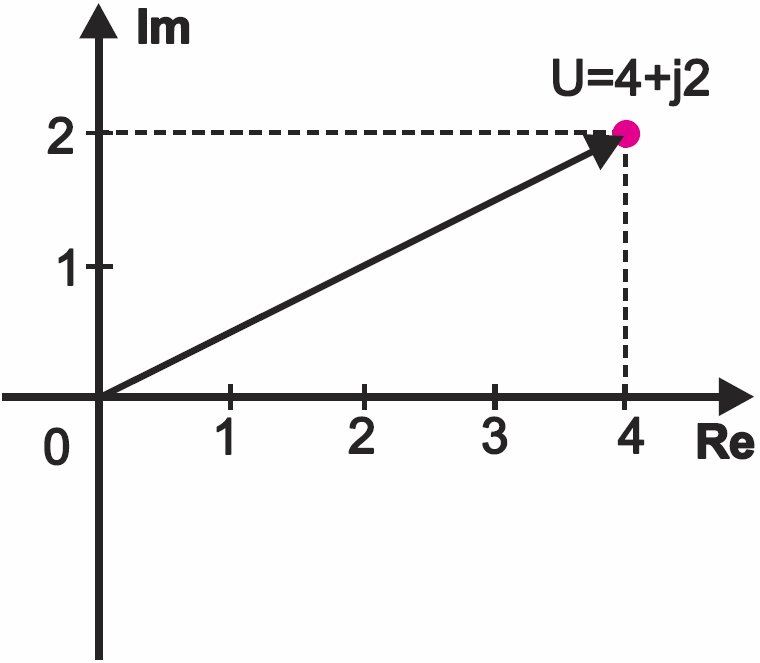
Przykładowo dla liczby U=4+j2 przedstawionej na rysunku 7 liczymy następująco:

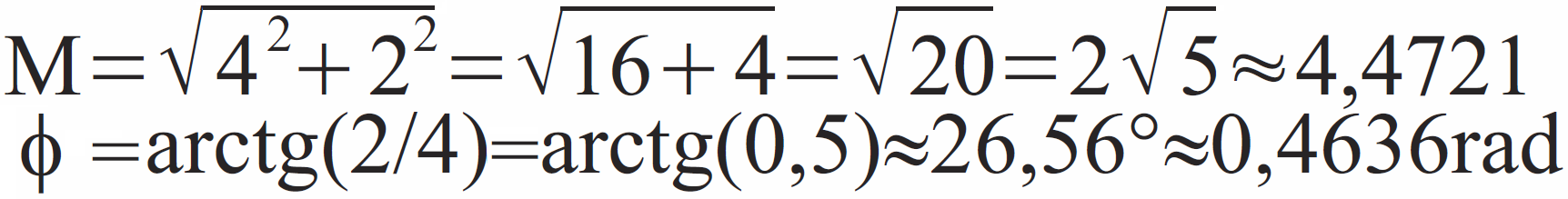
Można też liczyć „w drugą stronę”. Wystarczy przypomnieć szkolne definicje sinusa i kosinusa (sinα=y/r, cosα=x/r).

Znając moduł i argument obliczyć część rzeczywistą i urojoną: ℜ=M×cosφ ℑ=M×sinφ

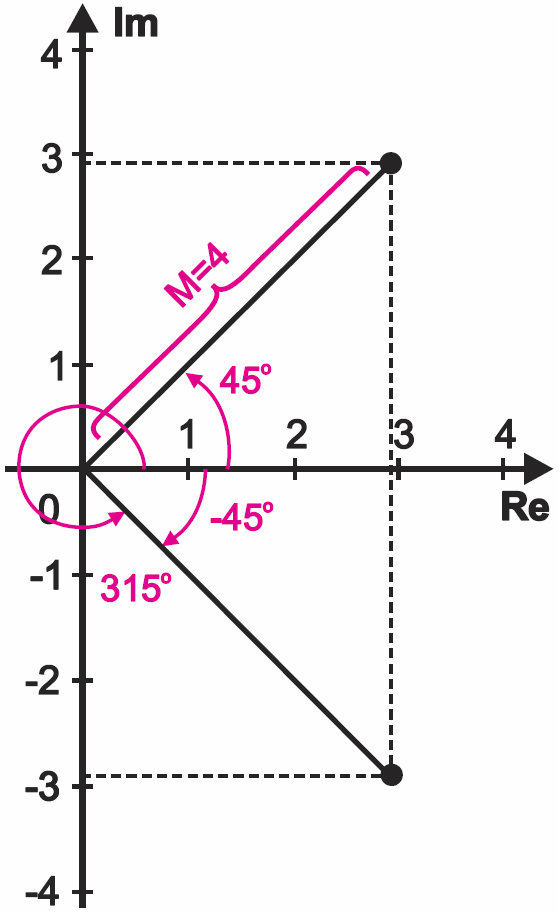
Zróbmy to dla dwóch prostych przypadków pokazanych na rysunku 8.

W obu przypadkach moduł wynosi 4. Dla liczby S kąt wynosi oczywiście 45 stopni. Dla kąta 45 stopni (π/4) zarówno sinus, jak i kosinus jest równy odwrotności pierwiastka z dwóch (1/√2 ≈ 0,707). Napiszemy:

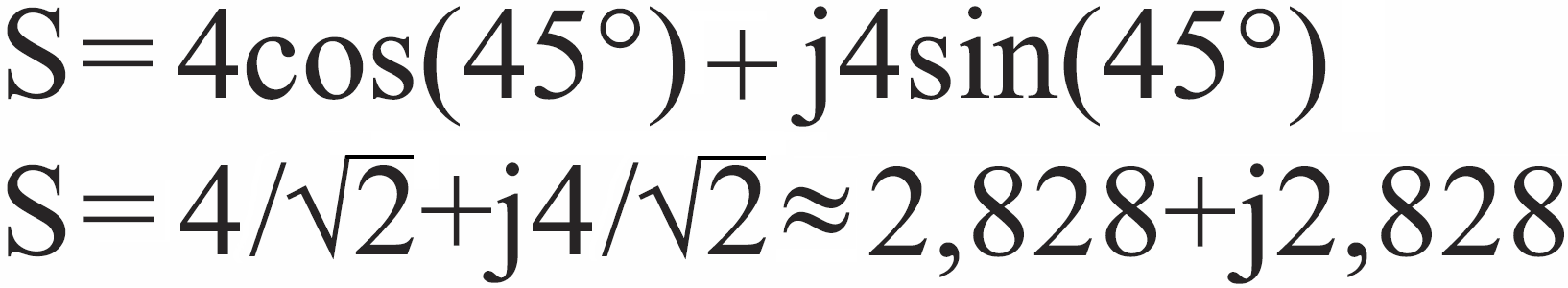
W przypadku liczby zespolonej T moduł także jest równy 4, natomiast kąt możemy podać albo jako φ=315° albo φ=–45°. Wynik będzie taki sam. Wiemy, że

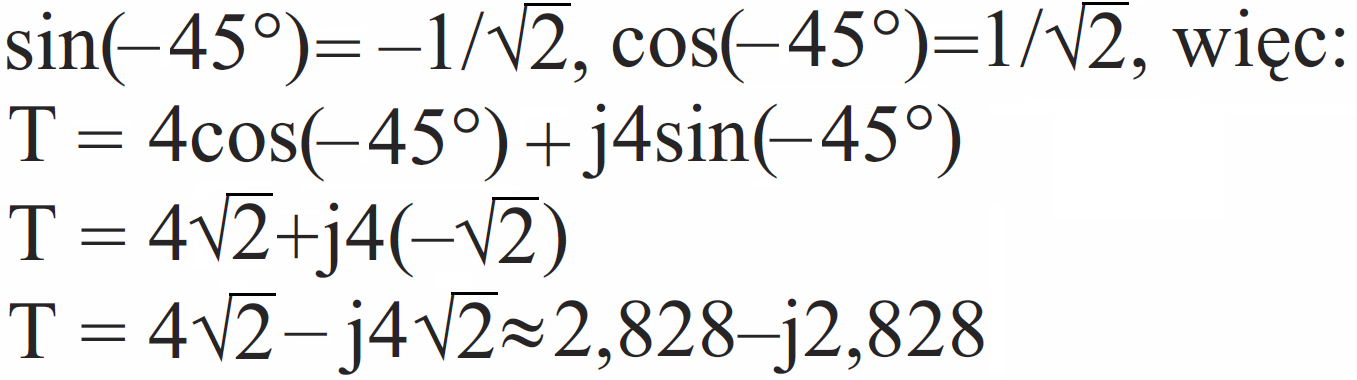
I oto poznałeś praktycznie postać trygonometryczną liczby zespolonej (zapis liczby zespolonej w postaci trygonometrycznej): Mcosφ + jMsinφ często spotyka się też zapis w postaci: z = |z|cosφ + j|z|sinφ. Ale to jeszcze nie wszystko. Musisz wiedzieć, że wykorzystujemy też postać wykładniczą liczby zespolonej. Znając moduł M i argument (wyrażony zazwyczaj nie w stopniach, tylko w radianach), piszemy po prostu: Me^jφ

Zapis na pewno prosty, ale dla przeciętnego zjadacza chleba być może nawet szokujący, bowiem w zapisie tym występuje liczba e – podstawa logarytmów naturalnych (2,718281828459….), która podnoszona jest do potęgi, a w wykładniku potęgi mamy „jednostkę urojoną” j. Nie bardzo mieści się to w głowie, bo niby dlaczego poniższa równość miałaby być prawdziwa Me^jφ = ℜ + jℑ = Mcos^φ + jMsin^φ

Intuicja nic tu nie pomoże. Żeby jednak nie pozostawić Cię w rozterce, wspomnę tylko, że równość taka wynika ze znanego od początków XVIII wieku tzw. wzoru Eulera, który matematycy, używający literki i zamiast j, zapisują następująco: e^ix = cosx + isinx

Wzór ten uzyskuje się przez rozwinięcie w szereg potęgowy funkcji e^x, sinx, cosx i odpowiednie pogrupowanie składników. Z grubsza biorąc, chodzi o to, że wiele funkcji, w tym także funkcje trygonometryczne, można przedstawić w postaci tzw. szeregów Taylora. To naprawdę wyższa matematyka. Nie musisz tego rozumieć, ale dla ciekawości poniżej znajdziesz wchodzące w grę zależności matematyczne.

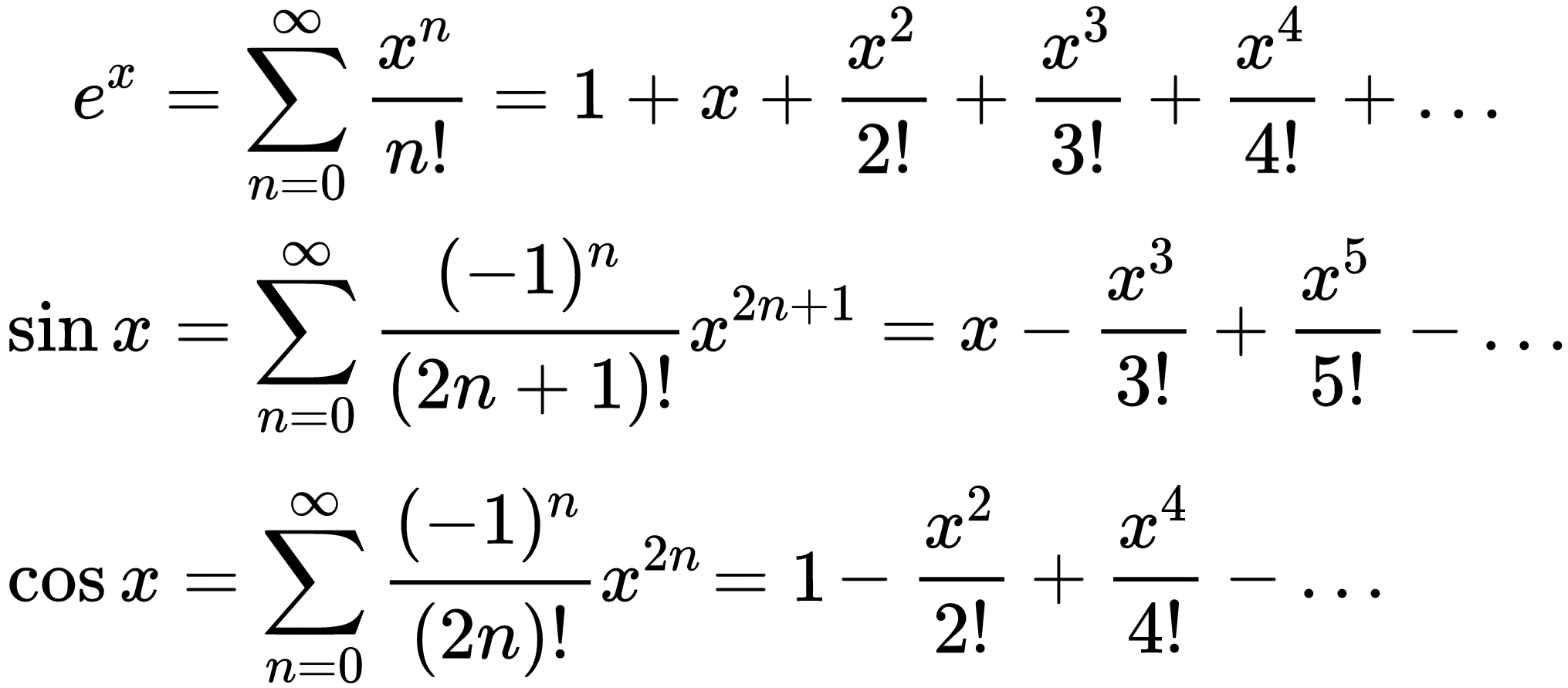
To naprawdę nie jest takie łatwe – może zaskoczy Cię też informacja, że wzór e^ix = cosx + isinx, podany przez Eulera w 1748 roku, został już wcześniej udowodniony w nieco innej postaci ln(cosx + isinx) = ix w roku 1714 przez Rogera Cotesa, natomiast praktyczne zastosowanie wzoru Eulera, wiążące liczby zespolone z płaszczyzną zespoloną, nastąpiło dopiero na przełomie XVIII i XIX wieku w pracy skandynawskiego matematyka Caspara Wessela.

Wbrew pozorom, strasząca początkujących, nieintuicyjna postać wykładnicza liczby zespolonej M^ej , okazuje się bardzo przydatna. Genialnie upraszcza bowiem przeprowadzanie mnożenia liczb zespolonych, ich dzielenia, potęgowania, pierwiastkowania i innych operacji.

Nieprzypadkowo też w poprzednim odcinku tak wnikliwie analizowaliśmy sens jednostki j, znaku minus i ich związków z obrotem reprezentacji graficznej liczby o 90 i 180 stopni. Teraz w ramach nieobowiązkowych zajęć domowych możesz samodzielnie przeanalizować przypadki szczególne dla kątów 0°, 90°, 180°, 270° oraz sprawę kompatybilności tego zapisu ze „zwykłymi liczbami”. Wykorzystaj rysunek 9. Zapisz i porównaj postacie algebraiczną, trygonometryczną i wykładniczą, obowiązkowo wyrażając kąt w radianach, a nie w stopniach. Pamiętaj, że liczba podniesiona do potęgi zerowej daje w wyniku jeden, a e^πi =–1 – przy okazji zetkniesz się tzw. tożsamością Eulera e^πi + 1 = 0 uznawaną za najpiękniejszy wzór w matematyce: wzór wiążący pięć fundamentalnych stałych matematycznych: liczbę 0, liczbę 1, liczbę π, liczbę e, jednostkę urojoną i, gdzie każde z podstawowych działań: dodawanie, mnożenie, potęgowanie, użyte jest tylko jeden raz.

Działania na liczbach zespolonych

Ogólnie biorąc, na liczbach zespolonych przeprowadzamy obliczenia podobnie jak na liczbach rzeczywistych. Jednak obliczenia są nieco trudniejsze.

I tak na przykład warto przeprowadzać dodawanie i odejmowanie liczb zespolonych zapisanych w postaci algebraicznej ℜ+jℑ. Wtedy odpowiednio dodajemy (odejmujemy) części rzeczywiste i części urojone. Przykładowo dla liczb A=4+j2, B=3–j5:
A+B =(4+3)+[j2+(–j5)]=7–j3
A–B=(4–3)+(j2–(–j5)]=1+j7

Liczby w postaci algebraicznej możemy w dość prosty sposób mnożyć, podobnie jak dwa wyrażenia w nawiasach:
A×B =(4+j2)×(3–j5)
= 4×3 + 4×(–j5) + j2×3 + j2×(–j5) = 12 + (–j20) + j6 + j²(–10) = 12 + (–j20 + j6) + –1(–10) = 12 + (–j14) + 10
A×B = 22–j14

Troszkę trudniej jest z dzieleniem liczb zespolonych w postaci algebraicznej. Wykorzystuje się tu pewną zależność, podobnie jak przy liczbach rzeczywistych: że dzielenie jest równoznaczne z pomnożeniem przez odwrotność (1/x) dzielnika: A / B = A × 1/B

Tylko jaka jest odwrotność liczby zespolonej? Otóż mnożymy przez tzw. liczbę sprzężoną, która ma taką samą część rzeczywistą i część urojoną z przeciwnym znakiem.

Ogólnie dla liczby a+jb liczba sprzężona to a–jb. W dalsze szczegóły nie będziemy wchodzić.

Musisz natomiast wiedzieć, że do mnożenia, dzielenia, potęgowania i pierwiastkowania genialnie nadaje się, na pozór tylko straszna, postać wykładnicza liczby zespolonej. Na przykład przy mnożeniu dwóch liczb zespolonych w tej postaci wystarczy pomnożyć ich moduły i dodać argumenty. Analogicznie przy dzieleniu: podzielić moduły i odjąć argumenty. Podobnie przy potęgowaniu i pierwiastkowaniu. Na przykład dla liczb:
C = 6e^j240°, D = 3e^j15°
C×D = 6e^j240°× 3e^j15°= 6×3e^{j(240°+15°)} = 18e^j255°
C / D = 6e^j240°/3e^j15°= 6/3e^{j(240°-15°)} = 2e^j225°
D³ = 3³e^j(3×15°) = 27e^j45°

I tak oto okazało się, że liczby zespolone idealnie nadają się do obliczeń impedancji. I nie tylko do tego. Liczby zespolone znajdują szerokie zastosowanie także do wielu innych obliczeń w obwodach sygnałów zmiennych, w tym w obwodach energetycznych sieci jedno i trójfazowych.

Od początku spróbuj utrwalić sobie fakt, że tak „prymitywne” elementy jak kondensatory, mają na tyle dziwne właściwości, że do opisania ich oporności nie wystarczą liczby rzeczywiste – potrzebne są liczby zespolone. Wprawdzie elektronik rzadko przeprowadza obliczenia na liczbach zespolonych, jednak przynajmniej ogólne pojęcie o tych kwestiach jest absolutnie niezbędne. Umożliwia bowiem uchwycenie sedna, a przynajmniej ogólnego zarysu wielu problemów spotykanych w praktyce. Natomiast brak takiej elementarnej wiedzy uniemożliwia zrobienie postępów, a nawet kieruje w stronę mistyki i magii. Tymczasem w elektronice nie ma magii – są tylko dość złożone zjawiska fizyczne, których nie sposób opisać za pomocą matematyki ze szkoły podstawowej czy gimnazjum.

W następnym odcinku wrócimy do jak najbardziej praktycznych zagadnień dotyczących kondensatorów, a potem także cewek.

Piotr Górecki