Elektronika (nie tylko) dla informatyków (19) Reaktancja indukcyjna

W poprzednim wykładzie rozprawialiśmy na temat energii zgromadzonej w cewce. W tym wykładzie zajmiemy się reaktancją indukcyjną.

Reaktancja indukcyjna cewki

Przy omawianiu kondensatorów okazało się, że reaktancja pojemnościowa X_C określona jest tylko dla przebiegów sinusoidalnych. W przypadku przebiegów o innych kształtach nie ma sensu mówić o reaktancji, a ewentualne obliczenia byłyby zbyt skomplikowane i musiałyby wiązać się z transformacją Fouriera. Natomiast fundamentalną cechą kondensatorów, która daje o sobie znać przy przebiegach o dowolnym kształcie, jest to, że prąd jest ściśle związany ze zmianami napięcia. Matematycznie rzecz biorąc, kondensator może realizować operację różniczkowania i całkowania.

Analogicznie jest z cewką indukcyjną. Tu napięcie jest ściśle związane ze zmianami prądu, co w uproszczeniu wyraża znana Ci już zależność:

U = L(ΔI/Δt)

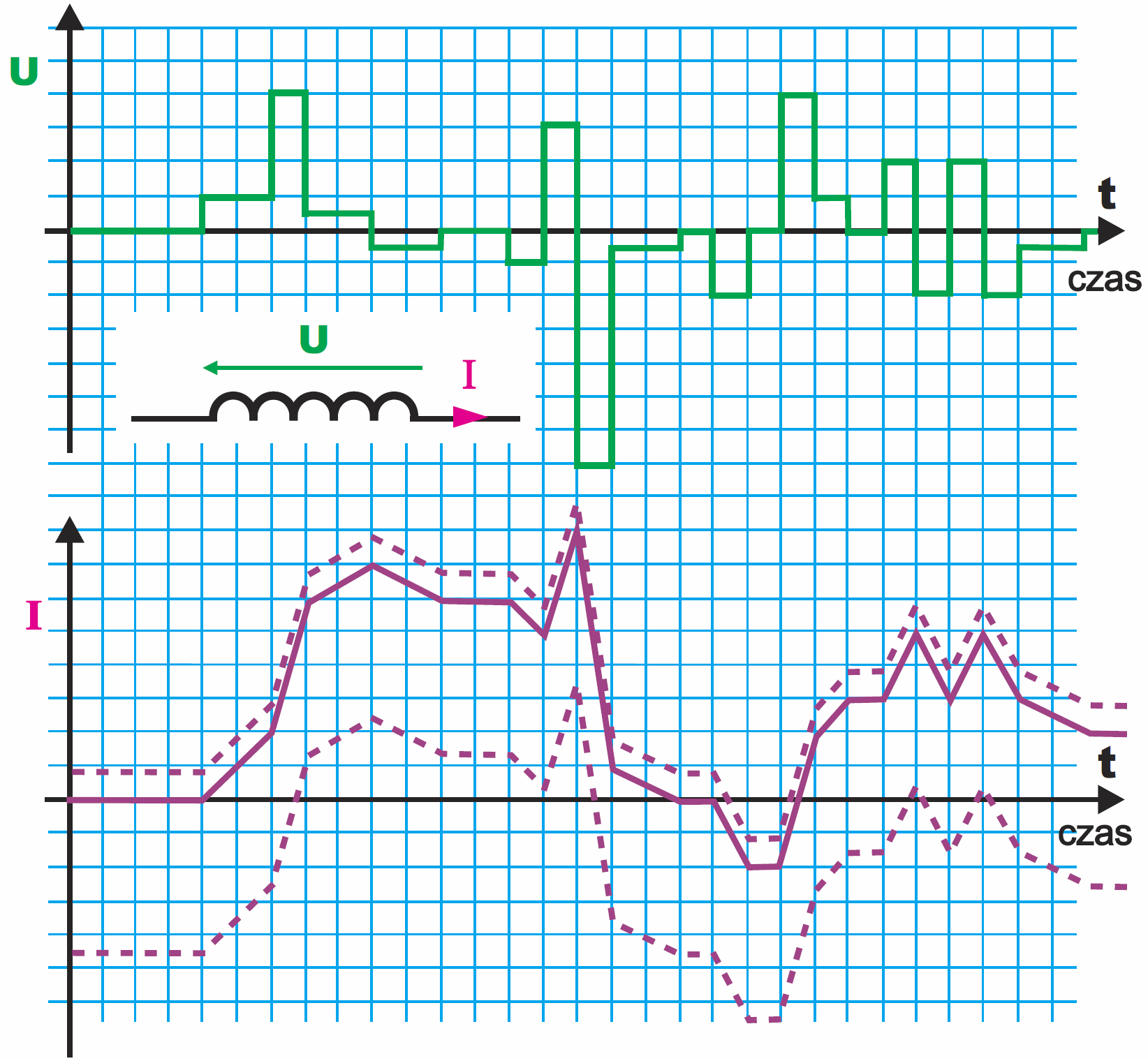
Koniecznie trzeba pamiętać, że w większości przypadków kształty napięcia i prądu w cewce różnią się, jak pokazuje przykład z rysunku 1. Zielony przebieg pokazuje napięcie na cewce. Ciągła czerwona linia pokazuje przebieg prądu w tej cewce, jeśli na początku prąd był równy zeru. Liniami przerywanymi pokazane są dwa przypadki, gdy prąd początkowy w cewce nie był równy zeru.

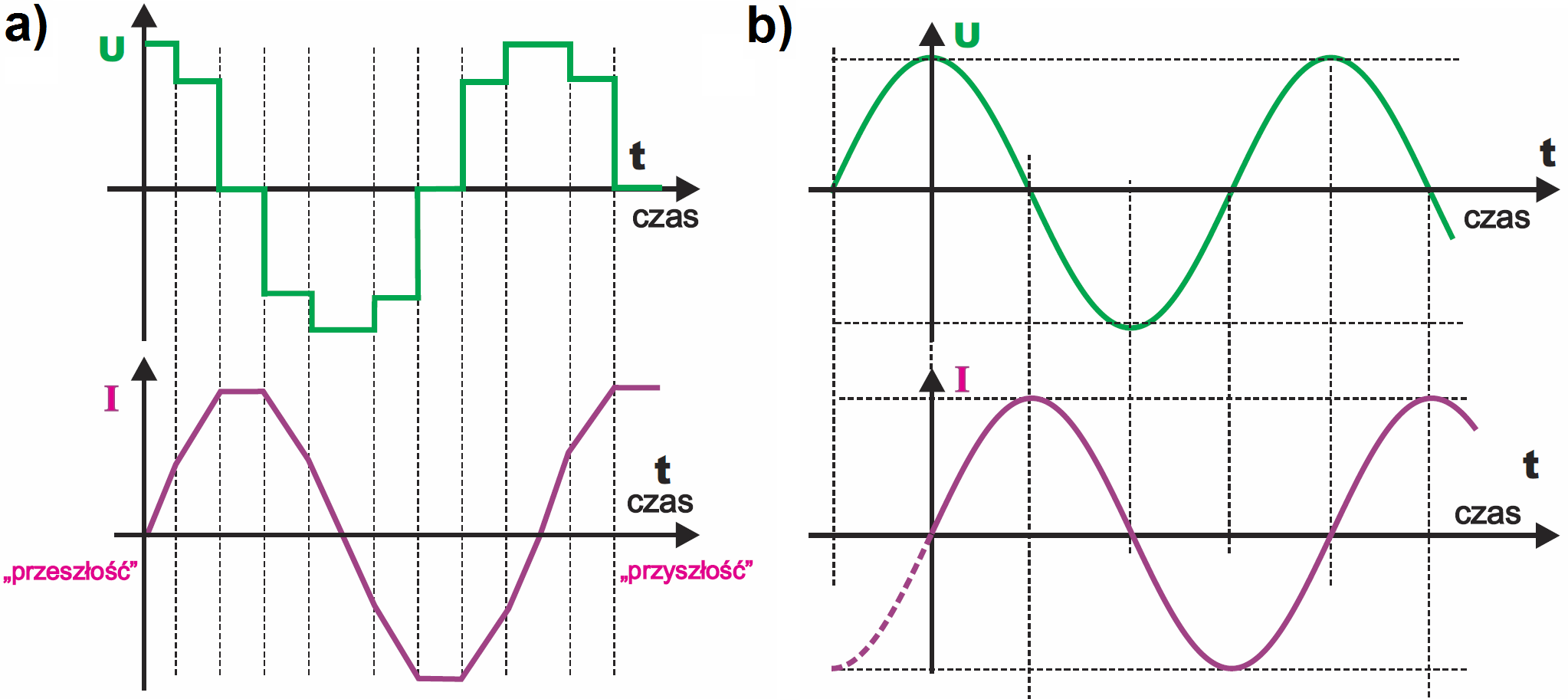
Nie dziw się temu! Zapamiętaj natomiast, że analogicznie jak w kondensatorze, także w cewce mamy do czynienia z całkowaniem i różniczkowaniem, dlatego kształty przebiegów tak się różnią. Tylko w przypadku przebiegu sinusoidalnego kształt przebiegów napięcia i prądu jest jednakowy – patrz rysunek 2. Podobnie, jak w przypadku kondensatora, występuje też przesunięcie, dokładnie o jedną czwartą okresu.

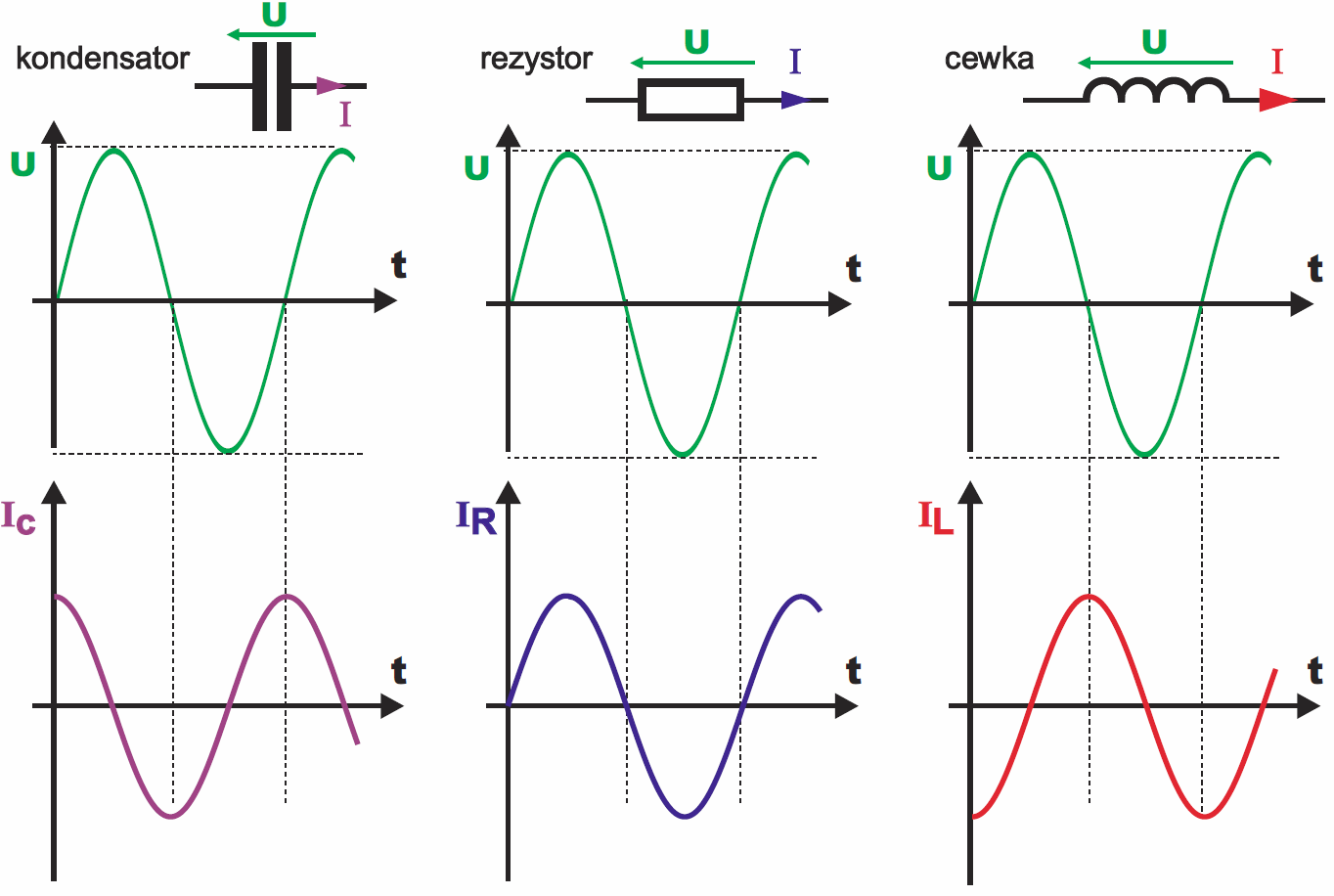
I znów możemy powiedzieć, że kondensatory i cewki są w pewnym sensie „odwrotne”, ponieważ jest to przesunięcie „w odwrotną stronę”, co ilustruje rysunek 3.

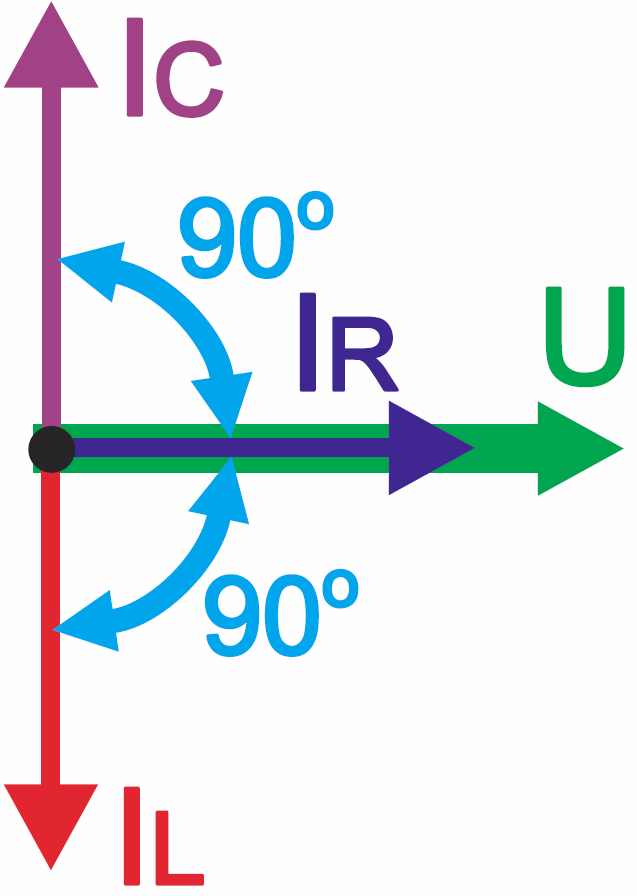
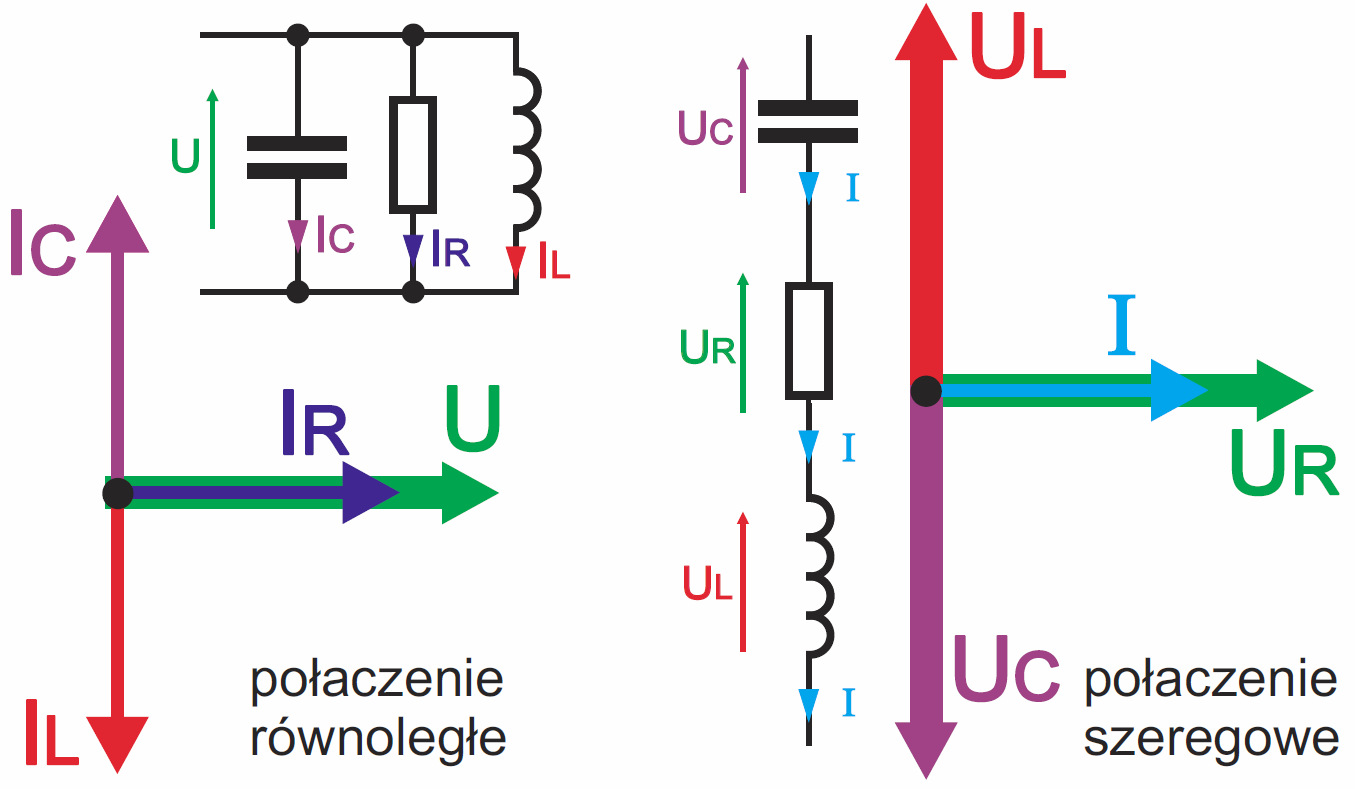
Jeszcze wyraźniej widać, to rysunku 4 – wykresie wskazowym, który odzwierciedla przebiegi z rysunku 3. Rysunek 4 przedstawia sytuację, gdy na elementach RLC występuje to samo napięcie, a to ma miejsce, gdy elementy te są połączone równolegle.

Gdyby elementy RLC były połączone szeregowo, będzie przez każdy z nich płynął ten sam prąd, a napięcia będą mieć różne fazy. Ilustruje to rysunek 5. Należy zauważyć, że przykłady z rysunków 3, 4, 5 są sztuczne pod tym względem – przyjęto na nich jednakowe wartości oporności (moduły impedancji) R, X_C, X_L, by pokazać główną ideę. W rzeczywistych obwodach RLC nie tylko mają one różne długości, ale „długość strzałek” zmienia się z częstotliwością. Do tego wrócimy już w następnym odcinku.

A na razie przeanalizuj podane rysunki i utrwal sobie główne zasady. Wcześniej mówiliśmy, że w kondensatorze prąd wyprzedza napięcie (nie łamiąc jednak zasady przyczynowości), a teraz powiemy, że w cewce prąd się opóźnia względem napięcia.

Wystarczy zapamiętać te dwie zasady: w cewce prąd opóźnia się względem napięcia, natomiast w kondensatorze prąd wyprzedza napięcie. Choć niektórym się to myli, Ty nie powinieneś mieć kłopotu, jeśli tylko zapamiętasz prosty żarcik – pytanie:

– Dlaczego w cewce prąd opóźnia się względem napięcia?

– Ponieważ zaplątuje się w zwojach!

Zaznaczając „wyprzedzanie” na wykresie wskazowym, mamy na uwadze obrót wektora w matematycznym kierunku dodatnim, czyli przeciwnie do wskazówek zegara. Natomiast analizując wyprzedzanie na wykresie czasowym, trzeba pamiętać, że po lewej stronie osi czasu mamy „przeszłość”, a po prawej „przyszłość”, jak to jest wskazane na rysunku 2.

A teraz o reaktancji indukcyjnej: zgodnie z wcześniej zdobytymi informacjami, powszechnie znany wzór X_L = 2πfL

nie jest pełny, ponieważ pozwala obliczyć tylko wartość liczbową reaktancji, którą nazywamy modułem, natomiast nie zawiera informacji o przesunięciu fazowym. Do matematycznych obliczeń obwodów RLC niezbędna jest informacja o fazie, czyli przesunięciu między prądem a napięciem. Do takich obliczeń trzeba używać liczb zespolonych. Jak łatwo się zorientować, dokładniejszy wzór na reaktancję cewki jest następujący: X_L = + jω = + j2πfL gdzie znak plus wskazuje na dodatnie przesunięcie fazy o π/2, czyli o 90 stopni. Jednak w praktyce pomijamy znak plus i piszemy: X_L = jω = j2πfL pamiętając o pominiętym znaku plus, który określa kąt przesunięcia dodatni, czyli przeciwny do ruchu wskazówek zegara.

Jeśli masz kłopot ze zrozumieniem powyższych informacji, musisz powrócić do wcześniejszych odcinków na temat kondensatorów, gdzie omawiana była także kwestia przekształcenia Fouriera, wykresów wskazowych i liczb zespolonych.

Dobroć

Wiadomo, że cewka gromadzi energię i że ma niejako „działanie dynamiczne” – energia jest zgromadzona w cewce wtedy, gdy płynie przez nią prąd. Początkującym może się to wydawać dziwne, ale właśnie tak jest: energia jest magazynowana tylko wtedy, gdy w cewce płynie prąd. A gdy nie ma prądu, nie ma też energii w cewce. I tu zaczyna się problem: tylko we wspomnianych w poprzednim odcinku nadprzewodnikach nie występują straty podczas przepływu prądu. We wszelkich innych cewkach, z którymi mamy do czynienia na co dzień, występują straty. Część energii dostarczonej do cewki jest tracona w postaci ciepła, a tylko część rzeczywiście jest magazynowana w cewce. Niewątpliwie ważnym pytaniem jest, jakie są proporcje między energią magazynowaną a traconą.

Moglibyśmy tu spróbować zestawiać i analizować wzory na energię E = LI²/2 oraz E = I², ale byłoby to zbyt skomplikowane. W każdym razie cewka od cewki różni się też wielkością strat, a raczej stosunkiem magazynowanej energii do strat energii na ciepło. Mówimy, że cewki mają różną dobroć.

Rzeczywiste cewki są dalekie od ideału. Ich uzwojenia mają jakąś niezerową rezystancję, więc przy przepływie prądu wydziela się w nich ciepło Joule’a (P=I²), a ponadto większość rzeczywistych cewek ma rdzeń z tzw. materiału ferromagnetycznego i dlatego występują tam jeszcze inne przyczyny strat energii (zamiany energii elektrycznej na ciepło). Należałoby przeanalizować te straty i porównać z ilością energii, magazynowanej w cewce. Zapamiętaj, że dobroć, oznaczana zwykle literą Q, jest nierozłącznie związana właśnie ze stratami energii, jednak w praktyce upraszczamy nieco zagadnienie i mówimy nie o stosunku energii, tylko o stosunku oporności: Q = X_L/R_S

Jedną z tych oporności jest reaktancja indukcyjna X_L = 2πfL, a drugą wypadkowa rezystancja reprezentująca straty R_S. Ta rezystancja R_S powinna reprezentować nie tylko rezystancję drutu, ale też wszelkie straty w cewce i jej rdzeniu. W pierwszym przybliżeniu możemy jednak sprawę uprościć i uważać, że R_S to rezystancja uzwojenia cewki.

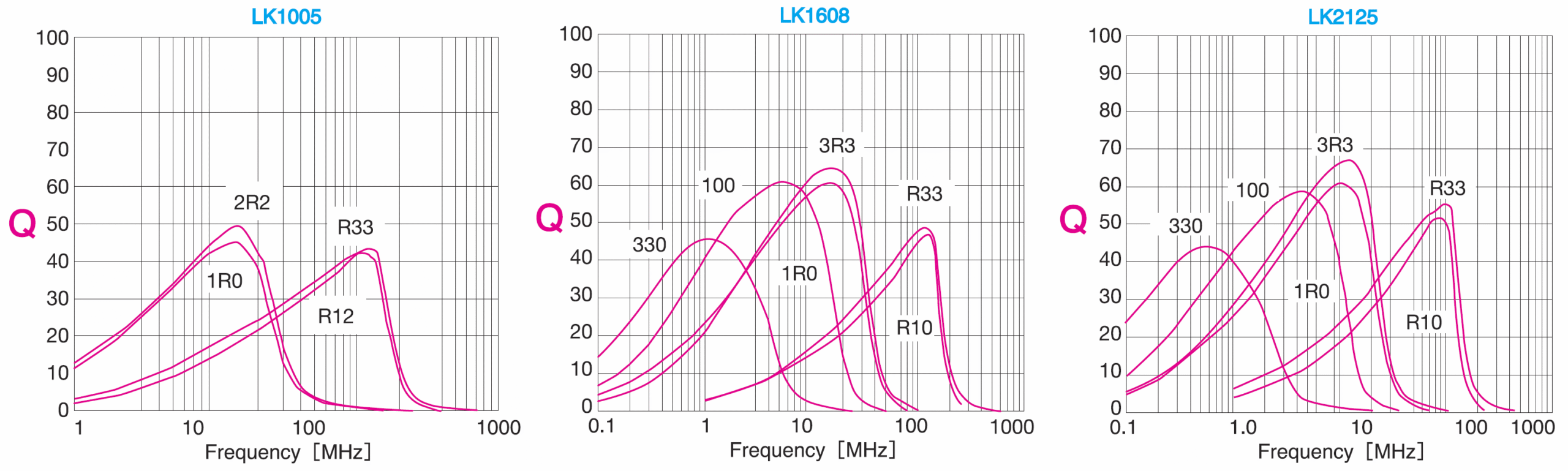
Po pierwsze, zauważ, że czym mniejsza rezystancja R_S, tym większa dobroć. Po drugie, zwróć uwagę, że reaktancja X_L rośnie ze wzrostem częstotliwości, a więc także dobroć Q powinna rosnąć ze wzrostem częstotliwości. I generalnie tak jest – dobroć rośnie ze wzrostem częstotliwości, jednak przy dużych częstotliwościach dają o sobie znać różne szkodliwe wpływy, jak np. tak zwane zjawisko naskórkowości i zwiększanie strat w rdzeniu. Dlatego wraz ze zwiększaniem częstotliwości dobroć wprawdzie rośnie, ale coraz wolniej, a przy dalszym zwiększaniu częstotliwości dobroć się zmniejsza. Ilustruje to rysunek 6, pochodzący z katalogu Taiyo-Yuden, dotyczący „drukowanych” cewek SMD serii LK. Wprawdzie są to cewki o bardzo małych indukcyjnościach (1R0 to 1 uH, R33 to 0,33 uH, a 330 to 33 uH), jednak w cewkach o większej indukcyjności jest podobnie.

Nie będziemy się zagłębiać w dalsze szczegóły choćby dlatego, że tak zdefiniowana dobroć nie jest kluczowym parametrem cewek. Owszem, parametr ten jest pożyteczny przy analizie i przy obliczeniach dotyczących różnych filtrów LC, ale filtry takie wykorzystywane są coraz rzadziej. Zwróć uwagę, że w definicji dobroci mamy do czynienia z reaktancją indukcyjną X_L, a ta jest określona tylko dla przebiegów sinusoidalnych. Tymczasem obecnie cewki coraz częściej pracują w obwodach zasilania, w tym w przetwornicach impulsowych, a tam przebiegi zmienne zupełnie nie przypominają sinusoidy, a ponadto często płynie przez nie także duży prąd stały. W takich zastosowaniach pojecie dobroci jako stosunku dwóch oporności (Q = X_L/R_S) niewiele się przyda. Owszem, w takich zastosowaniach ważną, a wręcz kluczową sprawą są straty energii, jednak są określane inaczej, niż za pomocą tak zdefiniowanej dobroci Q. Ponadto w grę wchodzi szereg innych czynników i problemów. W efekcie zagadnienie parametrów rzeczywistych cewek jest bardzo obszerne i skomplikowane. W ramach cyklu Elektronika dla Informatyków na pewno nie wyjaśnimy wszystkich szczegółów i subtelności. Jednak w dalszych odcinkach wrócimy do niektórych ważnych kwestii związanych ze stratami, żebyś miał przynajmniej ogólne pojęcie o problemach dotyczących cewek. A w następnym odcinku zajmiemy się sprawą rezonansu.

Piotr Górecki