Elektronika (nie tylko) dla informatyków (24) Równoległy obwód rezonansowy w praktyce

W poprzednim odcinku omawialiśmy różne zależności występujące w równoległym obwodzie rezonansowym. W tym odcinku skupimy się na praktyce, czyli na zastosowaniach równoległego obwodu rezonansowego w różnych obwodach.

Obwody rezonansowe w praktyce

Obwody rezonansowe od dawna pełniły i po części nadal pełnią rolę filtrów. Jednak współczesny elektronik rzadko ma do czynienia ze złożonymi filtrami LC, a co najwyżej z prostymi obwodami rezonansowymi, zazwyczaj równoległymi. Podstawowa zasada jest prosta: czym większa dobroć obwodu, tym węższe pasmo przenoszenia i zwykle zależy nam na uzyskaniu czy utrzymaniu dużej dobroci, ponieważ chcemy skutecznie filtrować sygnały. Warto mieć choć podstawową wiedzę o takich prostych filtrach.

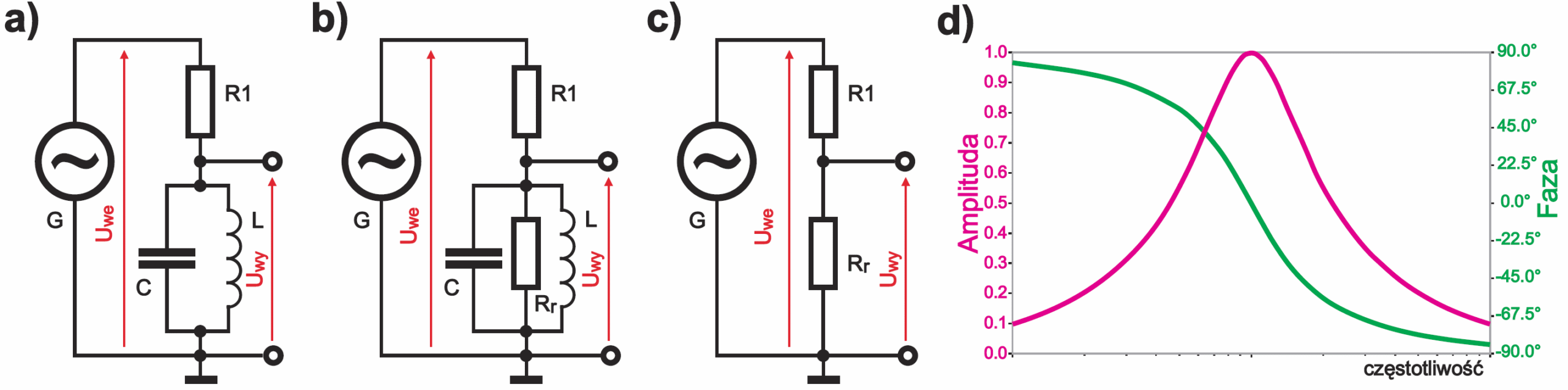
W praktyce często równoległy obwód rezonansowy włączony jest w szereg z rezystancją, z którą tworzy dzielnik napięcia – rysunek 1a. Tu sprawa jest dość prosta: jest to zwyczajny dzielnik. Nie możemy zapomnieć, że jest to rzeczywisty obwód ze stratami, które możemy przedstawić w postaci rezystancji równoległej R_r, jak na rysunku 1b. Przy częstotliwości rezonansowej f₀ nasz filtr-dzielnik uprości się do postaci jak na rysunku 3c i da na wyjściu największy sygnał. Natomiast dla innych częstotliwości sygnał wyjściowy będzie stłumiony i przesunięty w fazie mniej więcej jak na rysunku 1d.

Przy częstotliwość rezonansowej mamy dzielnik R1/R_r i oczywiście zależy nam na tym, żeby rezystancja R_r była jak największa. Gdy będzie dużo większa od R1, wtedy praktycznie cały sygnał wejściowy przejdzie na wyjście.

Ale elektronicy nie lubią cewek, a zwłaszcza ich nawijania. Często wykorzystują gotowe cewki, w tym miniaturowe dławiki, a te nie mają zbyt dużej dobroci. Niektórzy dodatkowo chcą przy tym okazać się sprytni i gotowi są zastosować cewkę o małej indukcyjności, a dla uzyskania potrzebnej częstotliwości rezonansowej chcą dołączyć do niej kondensator o dużej wartości. Owszem, uzyskają w ten sposób potrzebną częstotliwość rezonansową, ale…

Czy już widzisz, gdzie tu jest pułapka? Otóż „sprytna” próba wykorzystania małego dławika i dużego kondensatora wprawdzie zapewni potrzebną częstotliwość rezonansową, jednak jednocześnie oznacza, że rezystancja charakterystyczna będzie mała. Przecież:

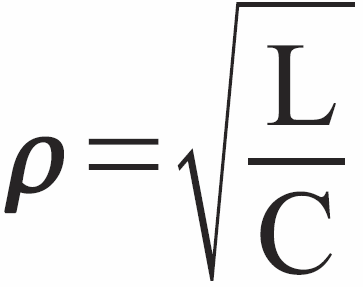
Mała cewka i duży kondensator tworzą obwód o bardzo małej oporności charakterystycznej.  A to oznacza, że będą tam płynąć duże prądy, które powodować będą straty choćby w rezystancji drutu cewki. W praktyce dobroć obwodu LC jest wyznaczona przez właściwości użytej cewki. To bardzo złożony temat, ale można w uproszczeniu stwierdzić, że czym większe wymiary ma cewka, czym ma więcej miedzi i „żelaza” (ferrytu), tym ma większą dobroć. Natomiast popularne małe dławiki ogólnie biorąc mają kiepską dobroć.

Pamiętamy też, że R_r = Q×ρ , więc jeśli i ρ, i Q będą małe, to i rezystancja R_r będzie niewielka. Wtedy okaże się, że nawet dla częstotliwości rezonansowej nasz filtr z rysunku 1 znacznie tłumi sygnał.

Ktoś zaproponuje, żeby w takim wypadku radykalnie zmniejszyć rezystancję R1…

Na pozór jest to dobry pomysł, bo tłumienie sygnału powinno się zmniejszyć. Owszem, tylko wtedy pojawi się kolejny problem.

Początkujący popełniają tu fatalny błąd. I to nie tylko w obwodach o małej oporności . Także jeśli obwód LC ma dużą dobroć, cieszą się z tej dobroci i… gotowi są zastosować rezystor R1 o małej wartości. Tymczasem rezystor ten psuje dobroć obwodu!

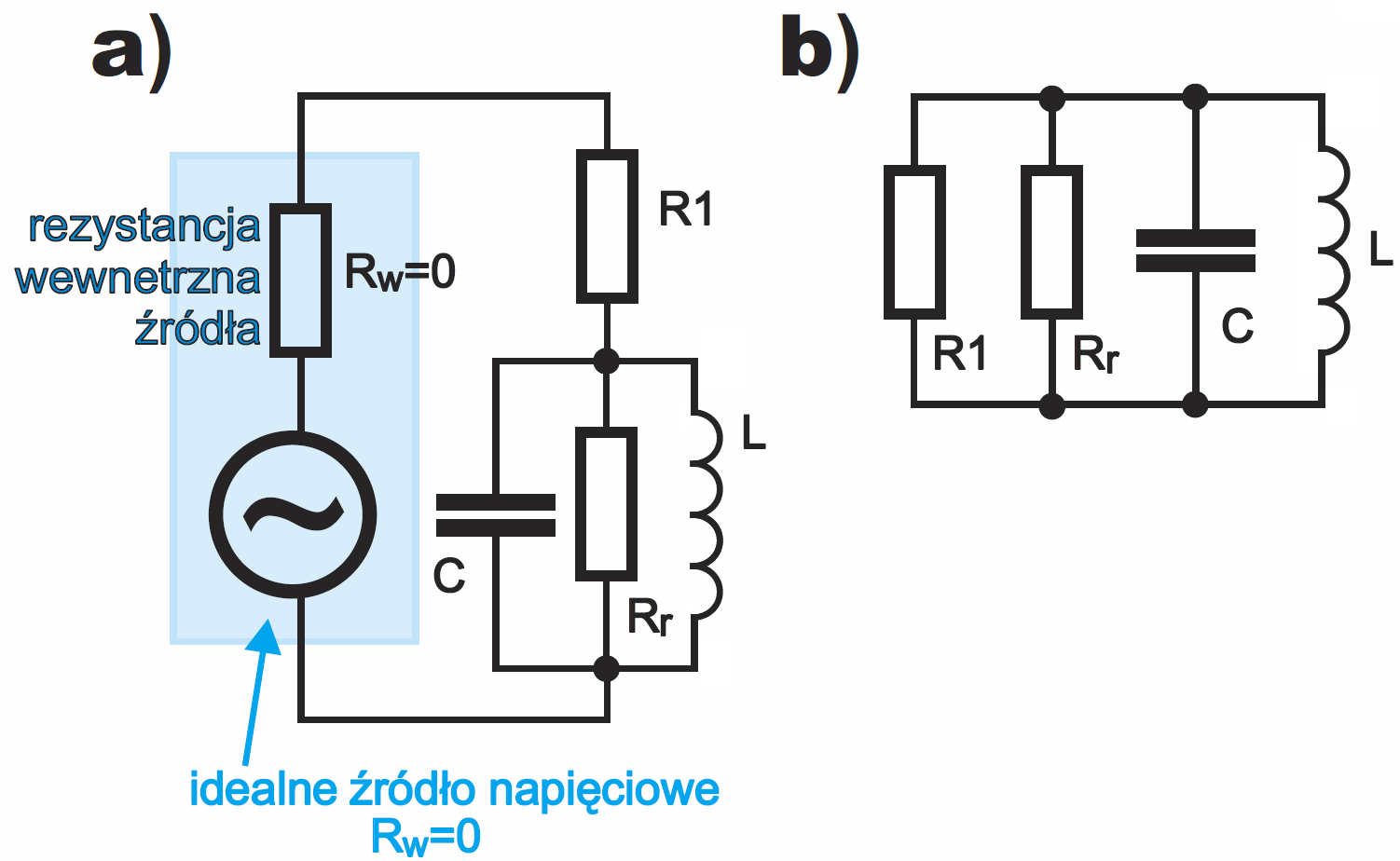
W podręcznikowych analizach obwodów równoległych, a także w naszych wcześniejszych rozważaniach, jako oczywisty traktowaliśmy fakt, że sygnał dostarczany jest z generatora, w którym amplituda napięcia jest niezmienna, niezależna od częstotliwości. Taki generator to idealne źródło napięciowe, a takie źródło ma, jak wiadomo, zerową rezystancję wewnętrzną – rysunek 2a. Oznacza to między innymi, że w filtrze-dzielniku z rysunku 1 rezystancja R1 zostanie dołączona równolegle (tak!) do rezystancji R_r i tym sposobem zepsuje dobroć obwodu LC! Ilustruje to rysunek 2b.

Popatrz na rysunki 1 i 2. Czy już widzisz, że wskazują one dwa sprzeczne kierunki działań? W praktyce rezystancja strat R_r jest wyznaczona przez obwód LC, sygnał przy częstotliwości f₀, chcielibyśmy zmniejszyć R1, zgodnie z rysunkiem 1, ale to spowoduje zmniejszenie dobroci, jak wskazuje rysunek 2b. Sprawa redukcji dobroci jest poważna, bo rezystancja R1 zazwyczaj jest znacznie mniejsza od R_r, a więc pogorszenie dobroci będzie poważne, może nawet niedopuszczalne. Ale nie będziemy wchodzić w dalsze szczegóły, bo chcę Ci tylko zasygnalizować ten poważny i dość trudny problem.

Okazuje się oto, że piękna idea filtru z rysunku 1a w praktyce okazuje się niełatwa do realizacji, zwłaszcza jeśli chcemy utrzymać dużą dobroć, czyli uzyskać wąskie pasmo przenoszenia i dobrą selektywność.

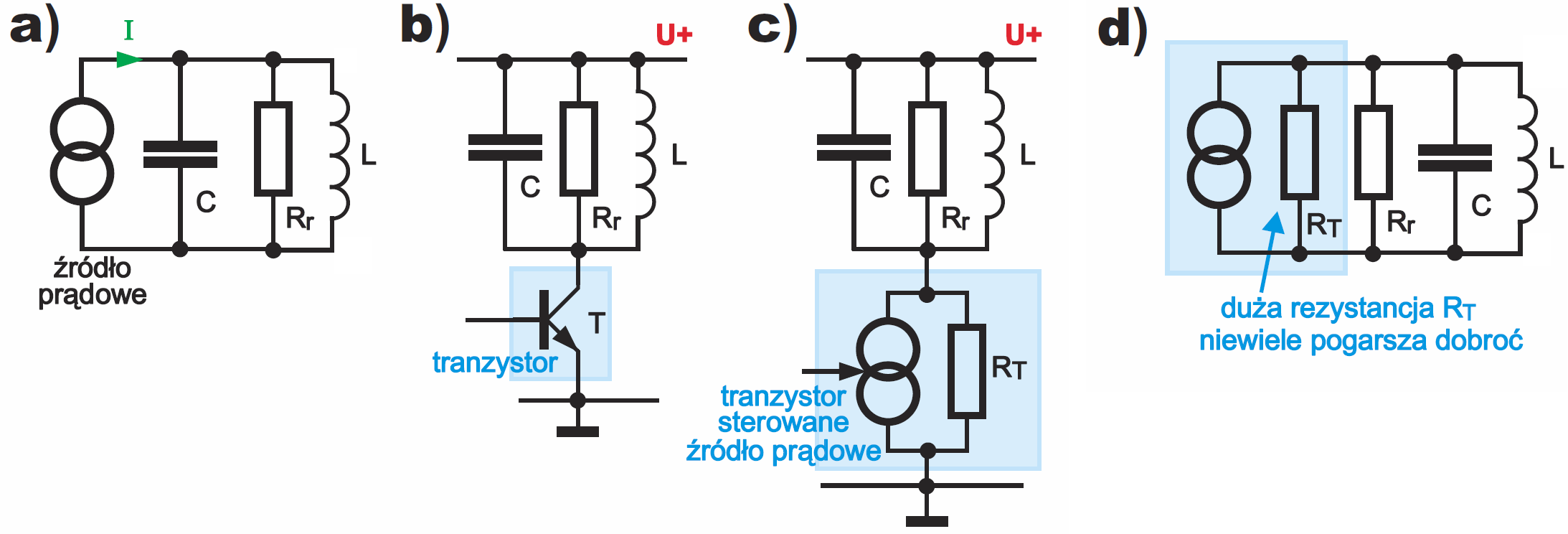
Jednak są inne możliwości. Przecież już wcześniej zauważyliśmy, że dla uzyskania dużej dobroci korzystne jest zwiększenie wartości R1. Idźmy tym tropem. Otóż najlepiej by było, gdyby równoległy obwód rezonansowy współpracował nie ze źródłem napięciowym i rezystorem R1 według rysunku 1a, tylko ze źródłem prądowym (oczywiście prądu zmiennego), ponieważ idealne źródło prądowe ma nieskończenie wielką oporność wewnętrzną. Wtedy niepotrzebny byłby w ogóle rezystor R1! Idea pokazana jest na rysunku 3a, a często spotykana realizacja – na rysunku 3b. Co prawda obwód kolektorowy tranzystora nie jest idealnym źródłem prądowym (rysunek 3c), ale jego rezystancja dynamiczna R_T dla przebiegów zmiennych jest duża, więc dodatkowe tłumienie wnoszone przez dużą rezystancję R_T jest niewielkie (rysunek 3d) i sytuacja jest zdecydowanie korzystniejsza, niż w układzie z rysunku 2b, gdzie był rezystor R1 o stosunkowo niedużej wartości.

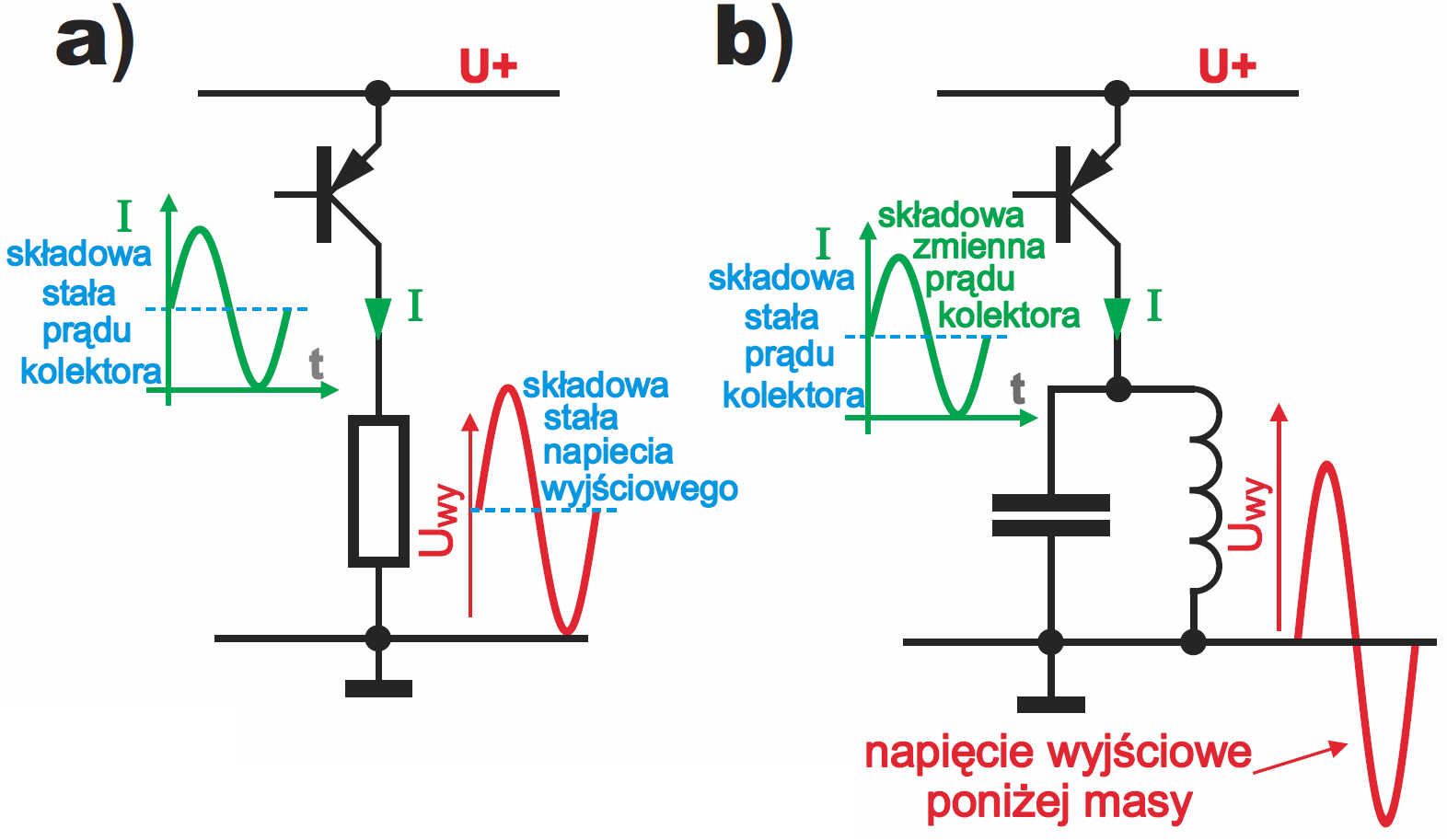
Zauważ, że po pierwsze, nie ma tu dodatkowego rezystora R1 o niedużej wartości, a po drugie, że napięcie wyjściowe wykroczy ponad dodatnie napięcie zasilania. To akurat nie jest nic dziwnego – w układzie z rysunku 1 (a także we wcześniej analizowanych obwodach) mieliśmy do czynienia z napięciami zmiennymi, które były symetryczne względem masy. Jednak w przypadku tranzystora z rysunku 3b jest to o tyle warte szerszego wyjaśnienia, ponieważ początkujący mają z tym kłopot. Jak wiadomo, prąd kolektora płynie tylko w jednym kierunku. Gdyby obciążenie było rezystorem, otrzymalibyśmy na nim napięcie o jednej biegunowości. Natomiast ku zdziwieniu początkujących, ten sam prąd jednokierunkowy, płynąc przez obwód rezonansowy, spowoduje powstanie na nim napięcia przemiennego. Nie jest to jednak nic dziwnego. Przeanalizujmy analogiczny obwód z tranzystorem PNP. Jak pokazuje rysunek 4a, prąd kolektora może być modulowany przebiegiem sinusoidalnym. Powiemy, że prąd ten zawiera składową stałą i składową sinusoidalnie zmienną. Na rezystorze prąd ten wywoła spadek napięcia, który też będzie miał składową stałą i składową zmienną. Natomiast w obwodzie z obwodem LC z rysunku 4b składowa stała, czyli mająca częstotliwość zero, przepływając przez obwód rezonansowy, spowoduje co najwyżej niewielki spadek napięcia stałego na rezystancji drutu cewki, który możemy spokojnie pominąć. Natomiast składowa zmienna prądu wywoła napięcie sinusoidalnie zmienne względem masy (porównaj wcześniejsze rysunki 3 w tym odcinku, oraz rysunek 4 w tym odcinku).

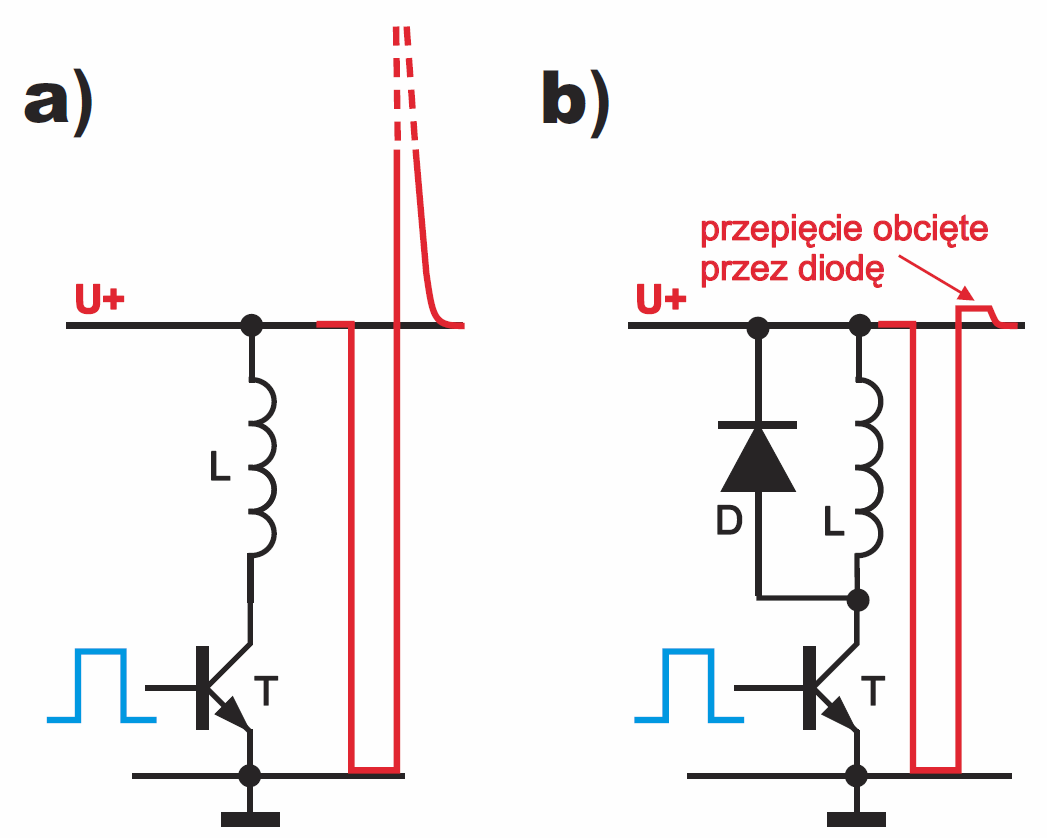
Chyba nie masz wątpliwości, że napięcie na obwodzie rezonansowym, włączonym w obwód kolektora lub drenu tranzystora, wykroczy poza napięcie zasilania. Z czymś podobnym mamy przecież do czynienia przy wyłączaniu cewki (np. przekaźnika) i dla ograniczenia przepięć włączamy diodę gaszącą – rysunek 5, tylko że tam impulsy napięcia występują jedynie podczas przerywania prądu w cewce, natomiast na obwodzie rezonansowym występuje przebieg sinusoidalny, praktycznie bez składowej stałej.

Idźmy dalej: a jaką wartość będzie mieć to napięcie wyjściowe?

Gdyby tranzystor był idealnym źródłem prądowym, wtedy zgodnie z rysunkiem 3a, zmienne napięcie wyjściowe, występujące przy częstotliwości rezonansowej f₀ na obwodzie LC, zależałoby tylko od rezystancji strat R_r i wielkości składowej zmiennej prądu: U_wy = I × R_r

Przy okazji warto podkreślić, że do obliczeń trzeba tu wziąć właśnie rezystancję R_r, a nie ρ. Oznacza to, że przy częstotliwości rezonansowej w cewce i kondensatorze popłyną prądy I_C, I_L wielokrotnie większe, niż składowa sinusoidalna prądu kolektora I. Jak już wiemy, prądy te będą Q razy większe od składowej zmiennej prądu kolektora I. Prądy I_C, I_L mogą osiągnąć dużą wartość, ale w praktyce ryzyko uszkodzenia występuje tylko w obwodach wysokiej częstotliwości i dużej mocy, np. w nadajnikach radiowych.

Rezystancja R_r jest zwykle duża, prąd możemy zwiększać, w razie potrzeby stosując tranzystor większej mocy, a to wskazuje, że…

można otrzymać na wyjściu dowolnie duże napięcie i to przy zachowaniu dużej dobroci Q!

Owszem, choć trzeba uwzględnić niedoskonałość tranzystorowego źródła prądowego, zobrazowaną na rysunku 3c i 3d. Dobroć zostanie zmniejszona wskutek równoległego połączenia rezystancji R_r i R_T, jednak rezystancja R_T generalnie jest dość duża i redukcja dobroci będzie zdecydowanie mniejsza niż w koncepcji z rysunku 1 i 2. Teoretycznie napięcie wyjściowe mogłoby więc być dowolnie duże, wielokrotnie większe od napięcia zasilania tego tranzystorowego układu. W praktyce ograniczeniem okazuje się tranzystor. Ale tą kwestią zajmiemy się w następnym odcinku.

Piotr Górecki