Elektronika (nie tylko) dla informatyków (26) Transformator idealny – ogólnie

W poprzednim odcinku zajmowaliśmy się między innymi teorią filtrowania przebiegów za pomocą równoległego obwodu rezonansowego LC. Od tego odcinka zmieniamy front i zaczynamy analizować właściwości transformatorów.

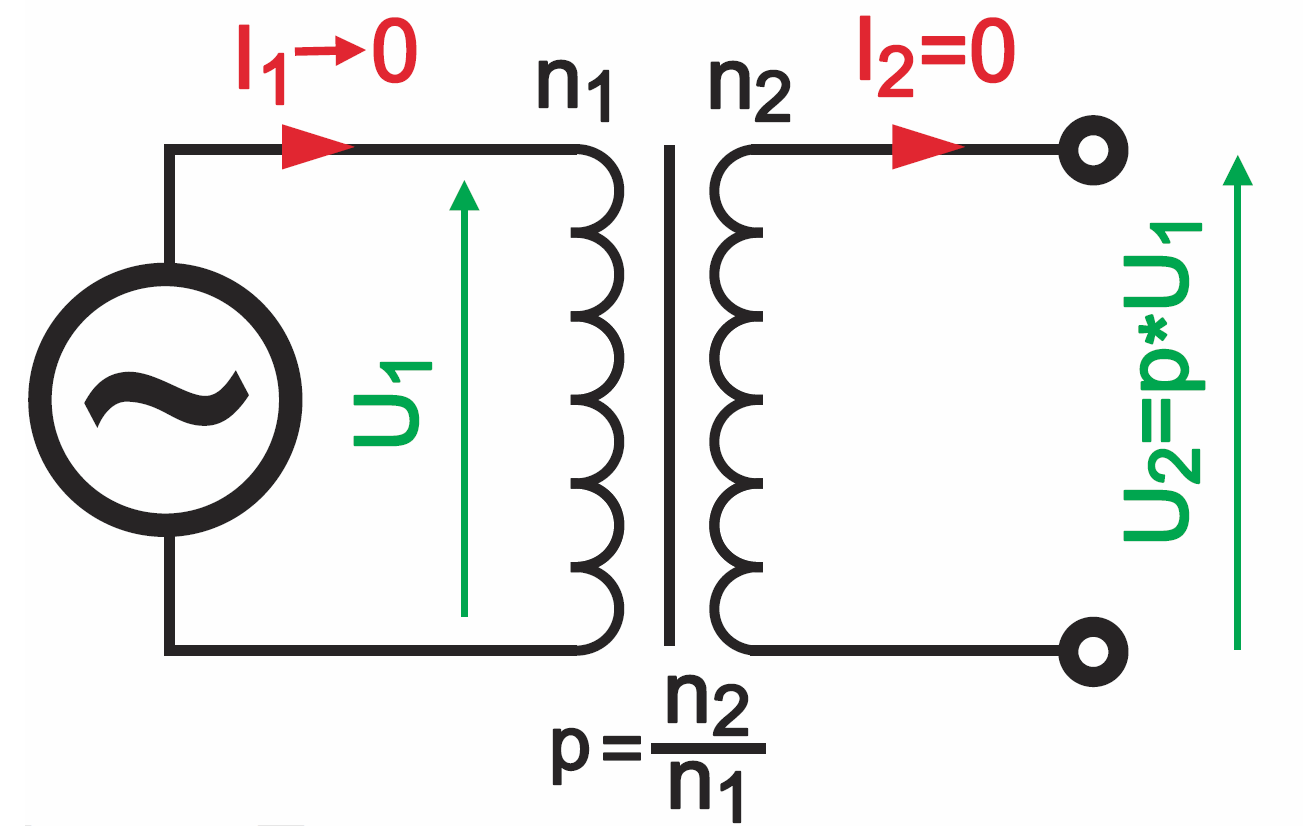
Transformator zazwyczaj kojarzy się z cewkami. Rzeczywiście, klasyczny transformator to dwie cewki, umieszczone blisko siebie. Schemat transformatora zazwyczaj rysuje się w postaci jak na rysunku 1, choć spotyka się też inne sposoby rysowania schematu transformatora, zwłaszcza transformatora (przekładnika) idealnego.

W szkole rozważane jest pojęcie indukcyjności wzajemnej, strumienia skojarzonego i inne zagadnienia, które wiążą transformatory z cewkami. I to wszystko jest prawdą. Jednak przy poznawaniu elementarnych właściwości transformatora wiązanie go z cewkami i ich właściwościami powoduje więcej kłopotu i zamieszania niż pożytku. Otóż zjawiska i problemy, występujące w rzeczywistych transformatorach o różnym przeznaczeniu, są dość skomplikowane i trudne do pełnej analizy. Początkujący po prostu się w tym gubią. Dlatego my na początek spróbujemy podejść do transformatorów inaczej, znacznie prościej, a dopiero potem będziemy analizować trudniejsze zasady i szczegóły.

Transformator idealny (przekładnik)

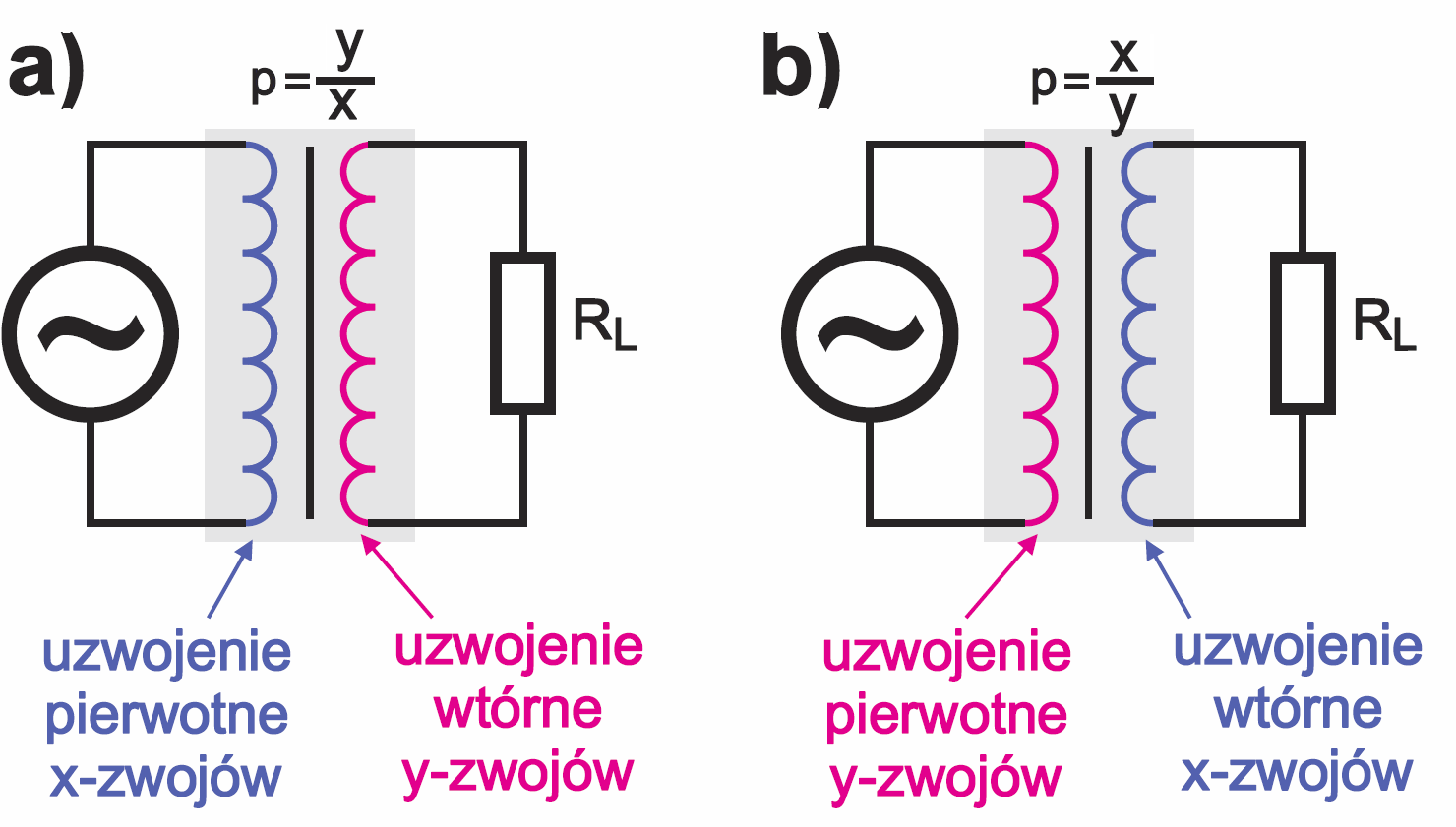
Najpierw podstawowa zasada: działanie transformatora polega na tym, że prąd zmienny, ściślej przemienny, przepływa przez uzwojenie pierwotne i wytwarza zmienne pole magnetyczne i strumień magnetyczny. To zmienne pole magnetyczne (zmienny strumień) indukuje napięcie w uzwojeniu wtórnym. Uzwojeniem pierwotnym nazywamy to, które dołączone jest do źródła energii, a do wtórnego dołączone jest obciążenie.

Ponieważ podstawą działania są zmiany pola magnetycznego, transformator nie może pracować przy prądach i napięciach stałych. W praktyce przy analizie ograniczamy się do pracy z przebiegami sinusoidalnymi, choć w zasadzie transformatory mogą pracować i pracują z przebiegami przemiennymi o różnych kształtach.

Zacznijmy od transformatora idealnego. Otóż taki idealny transformator, zwany często przekładnikiem, możemy sobie wyobrazić jako zestaw dwóch cewek o nieskończenie wielkiej indukcyjności, zerowych stratach, i co ważne, cewki te muszą być umieszczone tak blisko siebie, że pole magnetyczne jest wspólne dla obu cewek. Jeślibyśmy spełnili takie warunki, otrzymalibyśmy transformator idealny, którego właściwości… nie mają żadnego związku z cewkami.

W takim transformatorze nie ma żadnych strat, więc cała moc jest przekazywana z wejścia na wyjście. Napięcia i prądy zależą wyłącznie od stosunku liczby zwojów uzwojenia wtórnego i pierwotnego. Nazwijmy przekładnią p stosunek liczby zwojów uzwojenia wtórnego n₂ do liczby zwojów uzwojenia pierwotnego n₁ (p = n₂/n₁). I właśnie przekładnia p decyduje o wszystkim, i to w beznadziejnie prosty sposób. Mianowicie przy takim zdefiniowaniu przekładni, wystarczy zapamiętać prościutkie zasady:

1. Napięcie wyjściowe (wtórne) jest p-krotnie większe od wejściowego (pierwotnego).

2. Prąd wyjściowy (wtórny) jest p-krotnie mniejszy od wejściowego (pierwotnego).

3. Rezystancja jest transformowana w stosunku p².

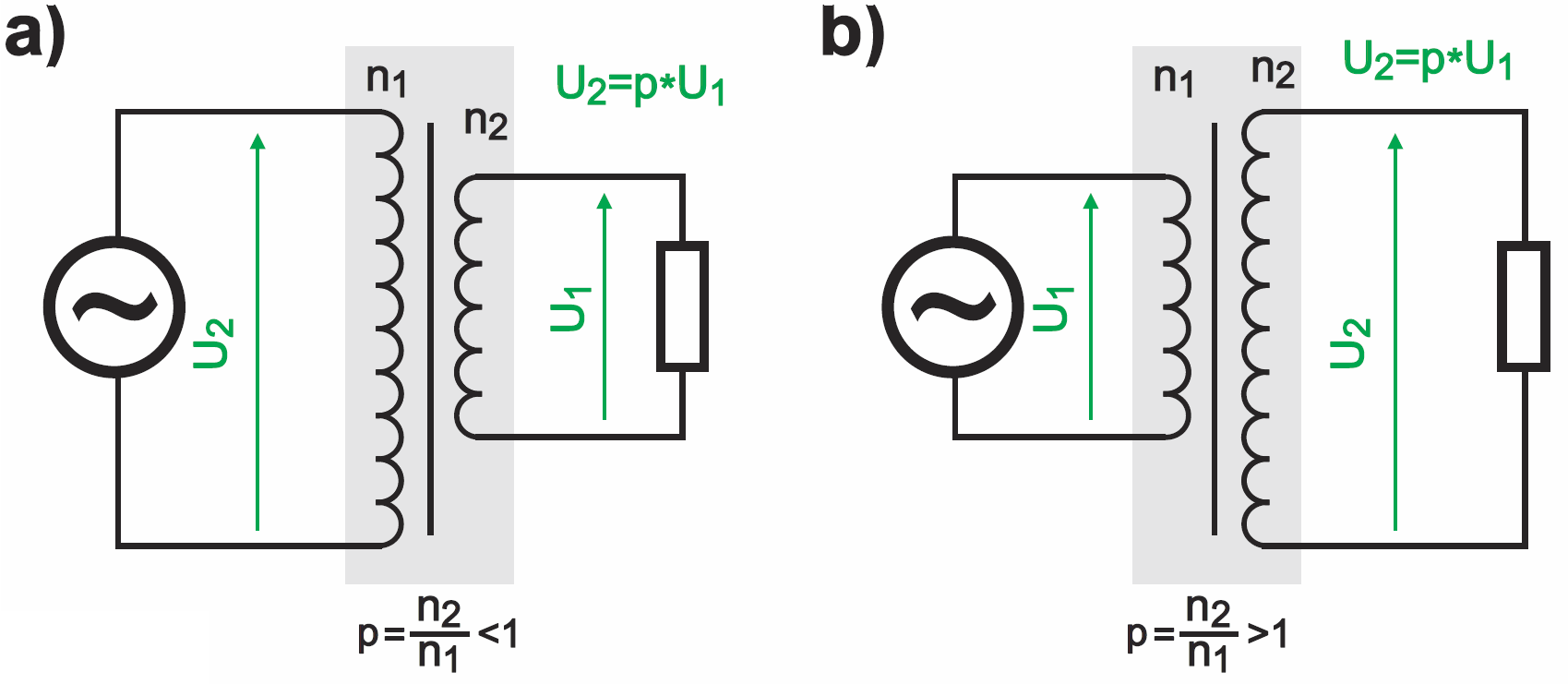
Pierwsza zasada jest łatwa do intuicyjnego zaakceptowania: otóż napięcie jest wprost proporcjonalne do liczby zwojów, więc czym więcej zwojów w uzwojeniu wtórnym, tym wyższe jest napięcie wyjściowe. Jeśli przyjęliśmy, że przekładnia p to stosunek liczby zwojów uzwojenia wtórnego do pierwotnego (p = n₂/n₁), to taka sama zależność obowiązuje dla napięć: p = U₂/U₁ Napięcie wyjściowe obliczamy wtedy: U₂ = p×U₁ Ilustruje to rysunek 2. Gdy napięcie wtórne jest mniejsze od pierwotnego (gdy p<1), mówimy o transformatorze obniżającym – rysunek 2a. Jeśli zwojów w uzwojeniu wtórnym jest więcej niż w pierwotnym, napięcie wyjściowe będzie większe od wejściowego – mamy transformator podwyższający rysunek 2b.

Transformator nie ma ściśle określonego wejścia i wyjścia, więc można go „odwrócić”, jak pokazuje rysunek 3, i z obniżającego uzyskać podwyższający (a także odwrotnie), co oznacza zmianę przekładni z p na 1/p.

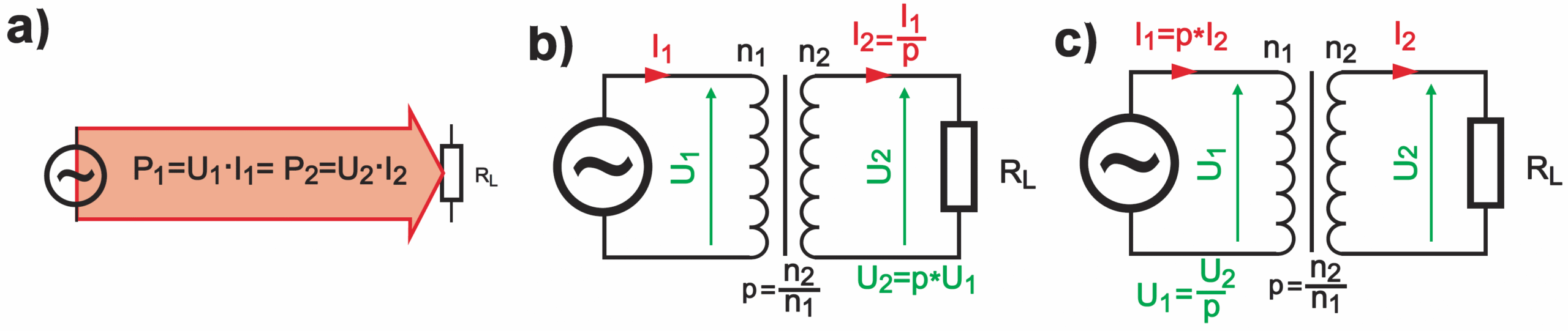
Transformator nie jest ani źródłem energii, ani nawet magazynem energii. Możemy powiedzieć, że cała moc dostarczana ze źródła zasilania jest na bieżąco przekazywana do obciążenia – patrz rysunek 4a. W transformatorze idealnym nie ma żadnych strat, więc moc P₁ = U₁×I₁ pobierana ze źródła jest równa mocy P₂ = U₂×I₂ dostarczanej do obciążenia. A jeśli tak, to prąd pobierany ze źródła zasilania (mającego napięcie U₁) wynosi: I₁ = P₁/U₁

Ale ponieważ P1 = P2 = U₂×I₂, możemy napisać: I₁ = P₂/U₁ = U₂×I₂/U₁ a to oznacza, że: I₁/I₂ = U₂/U₁ = N₂/N₁ = p Zależności te ilustruje rysunek 4b. Można także przedstawić te same zależności liczbowe niejako w drugą stronę, jak pokazuje rysunek 4c.

Jak widać, podstawowym parametrem transformatora jest przekładnia (stosunek liczby zwojów), która zasadniczo określa stosunek napięć, ale w konsekwencji także prądów. Co bardzo ważne, dotyczy to zarówno stanu bez obciążenia, jak i przy obciążeniu uzwojenia wtórnego rezystancją R_L.

Tu ktoś może zapytać, jaką wartość ma mieć rezystancja R_L?

Otóż w transformatorze idealnym może mieć wartość dowolną! W transformatorze idealnym (przekładniku) w sytuacji bez obciążenia, czyli w tzw. stanie jałowym, żadne prądy nie płyną. Ściślej: prąd pierwotny I₁ jest nieskończenie mały, a prąd wtórny na pewno jest równy zeru, bo uzwojenie to nie jest nigdzie podłączone. Przekładnia p decyduje, jakie jest napięcie na takim nieobciążonym wyjściu – rysunek 5. Prądy nie płyną, ale napięcie wyjściowe występuje i transformator jest „gotowy” do pracy w warunkach obciążenia. Jeśli teraz do wyjścia, czyli do uzwojenia wtórnego dołączymy rezystancję obciążenia R_L, to popłynie przez nią prąd I₂. O jakiej wartości?

Na wyjściu cały czas będzie występować napięcie U₂, wyznaczone przez przekładnię p (U₂ = p × U₁). Wartość płynącego prądu wtórnego będzie więc wyznaczona przez napięcie U₂ i przez rezystancję R_L: I₂ = U₂/R_L W ten sposób transformator dostarczy do obciążenia moc: P₂ = U₂×I₂ Ta moc musi być pobrana ze źródła zasilania: P₂ = P₁= U₁×I₁

Widać, że to obciążenie R_L decyduje, jakie będą prądy i moc przenoszone przez transformator ze źródła energii do obciążenia. Natomiast o napięciach decyduje napięcie źródła U₁ i przekładnia p.

W transformatorze idealnym nie ma żadnych ograniczeń na moc, więc teoretycznie moc przekazywana do obciążenia i prądy mogą być dowolnie duże, czyli rezystancja R_L dowolnie mała. Jak widać, jedynym parametrem transformatora idealnego jest przekładnia p.

Zupełnie początkujący czasem pytają, skąd transformator wie, jakie mają być prądy i jaką moc ma „przepuścić”? Otóż transformator niczego nie musi wiedzieć. Najprościej można to wyjaśnić tak:

(1) podstawowa zależność to stosunek napięć, wyznaczony przez stosunek liczby zwojów obu uzwojeń, czyli przekładnię p. Tak więc w pierwszej kolejności mamy do czynienia z transformacją napięć.

(2)  A jeśli napięcie wtórne U₂ jest określone przez przekładnię, to prąd wtórny I₂ zależy tylko od rezystancji obciążenia.

(3) Natomiast prąd pierwotny I₁ popłynie taki, żeby moc pobierana ze źródła była w całości dostarczana do obciążenia. Czyli po prostu prąd pierwotny dostosowuje się do obciążenia R_L.

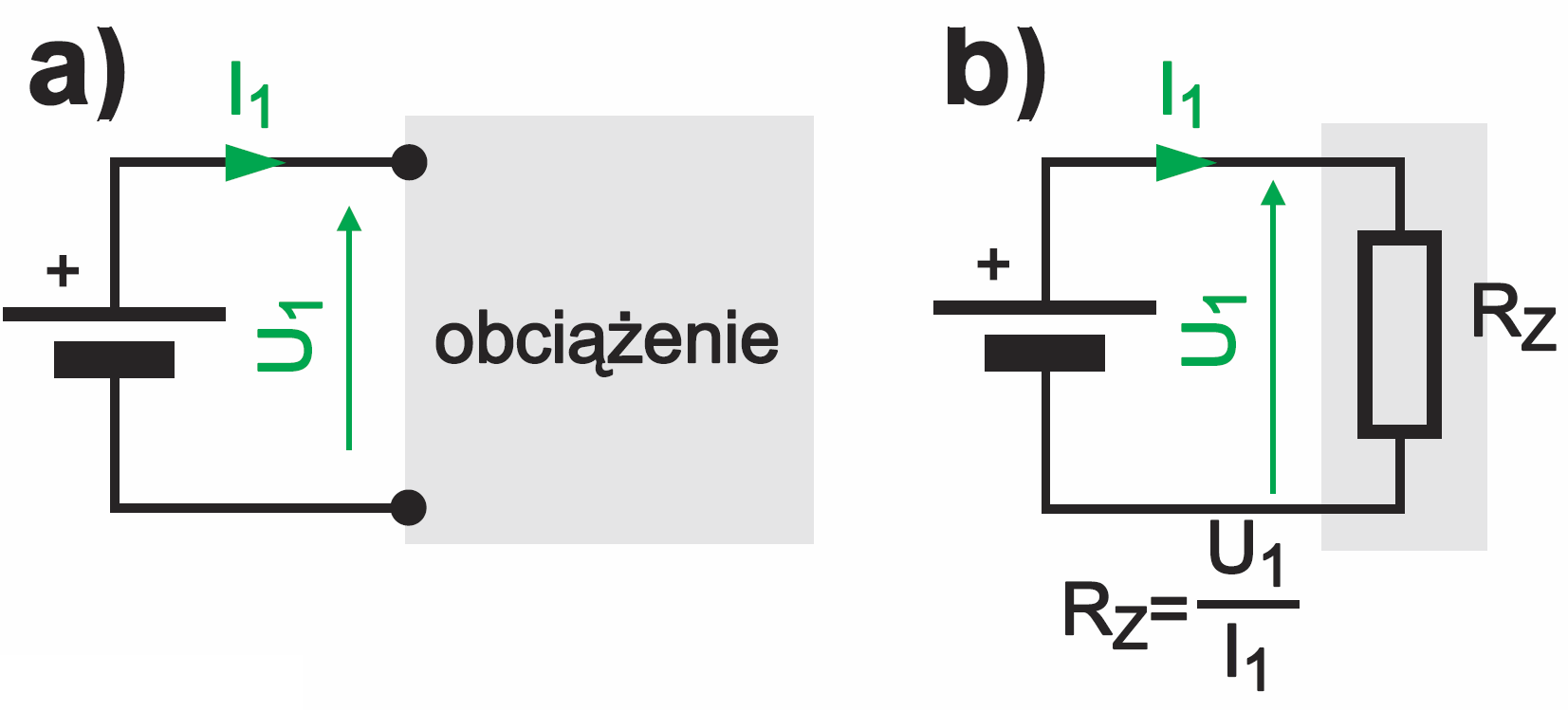
Koniecznie trzeba też zrozumieć i zapamiętać, jakie ma to znaczenie z punktu widzenia oporności. Spróbujmy odpowiedzieć na pytanie, jaką oporność (rezystancję) „widzi” źródło zasilania, do którego podłączony jest transformator obciążony rezystancją R_L? Zacznijmy od tego, że zastępcza rezystancja obciążenia, „widziana” przez źródło, określona jest przez stosunek napięcia i prądu. Z prawa Ohma wynika, że R = U/I. Źródło E widzi obciążenie z rysunku 6 jako rezystancję R_Z= U₁/I₁. Podobnie jest przy prądach sinusoidalnie zmiennych w naszym transformatorze.

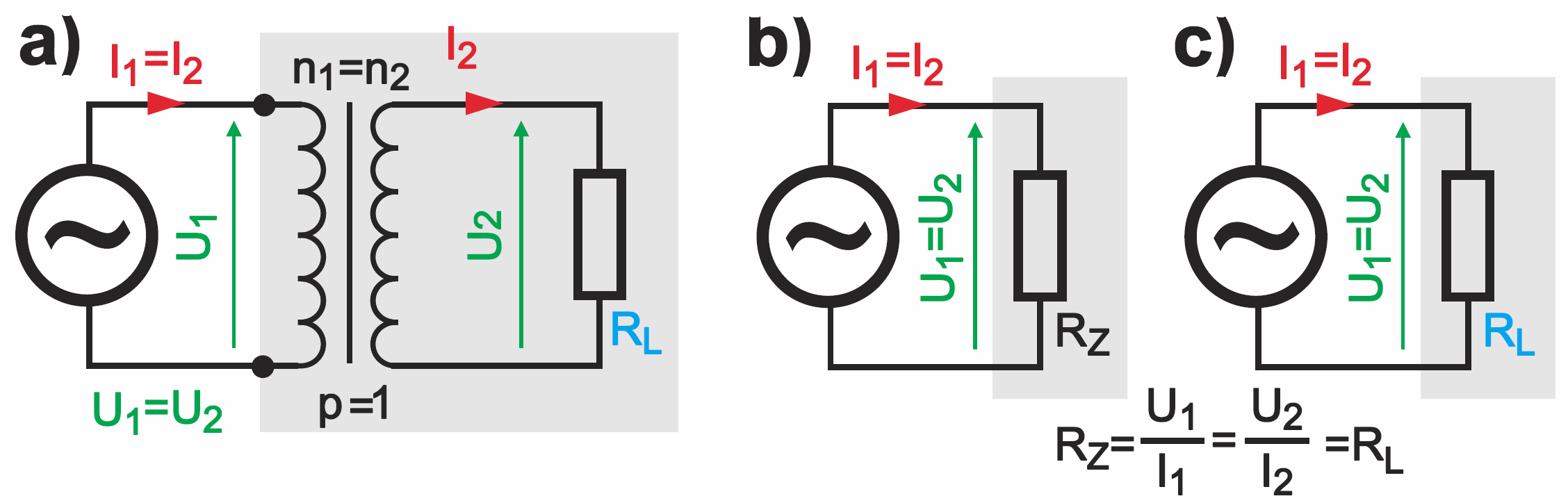
Zacznijmy od oczywistego przypadku: transformator idealny o przekładni p=1 jest „przezroczysty”; sytuacja jest taka, jakby go nie było – rysunek 7. Czyli w sumie źródło zasilania widzi taki transformator z obciążeniem R_L, po prostu jako rezystancję R_L. Jednak jeżeli transformator ma przekładnię różną od jedności, wtedy źródło widzi taki zestaw jako rezystancję o wartości większej lub mniejszej niż R_L.

Oto wyliczenie matematyczne: rezystancja zastępcza R_Z, widziana przez źródło sygnału, zawsze wynosi: R_Z = U₁/I₁

Natomiast analogiczna zależność dla rezystancji R_L:

R_L= U₂/I₂ Interesuje nas stosunek:

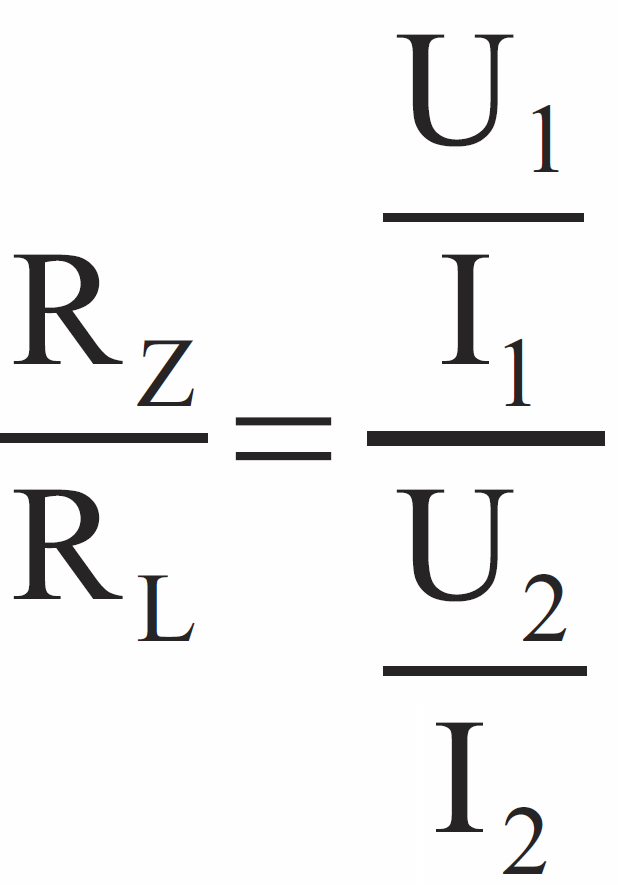
a to oznacza że:

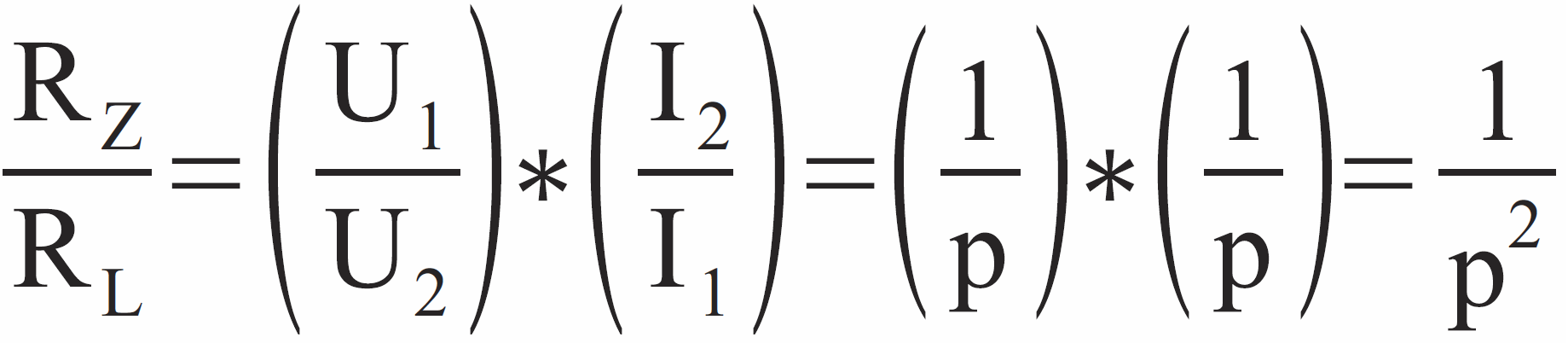
Jak z tego wynika, rezystancja zostaje przetransformowana ze współczynnikiem 1/p². Mówimy potocznie, że w transformatorze rezystancja transformuje się z kwadratem przekładni.

Możemy to zapisać w innej postaci, bo
jeśli R_Z/R_L = 1/p², to:

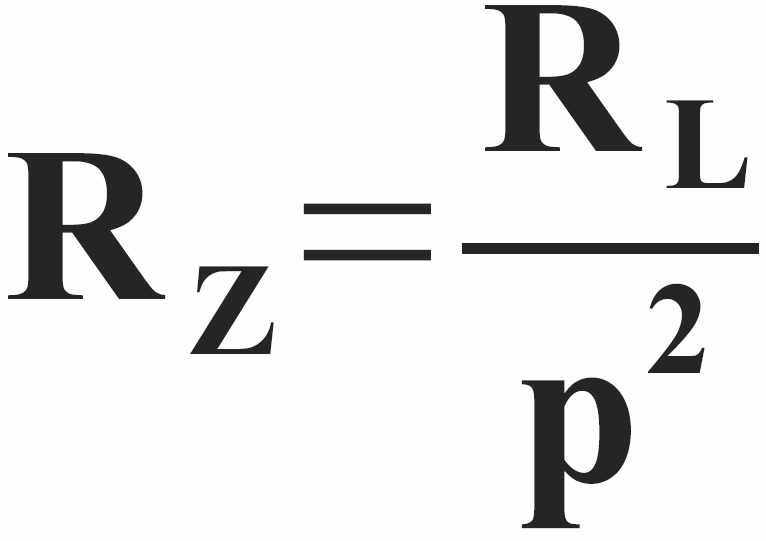
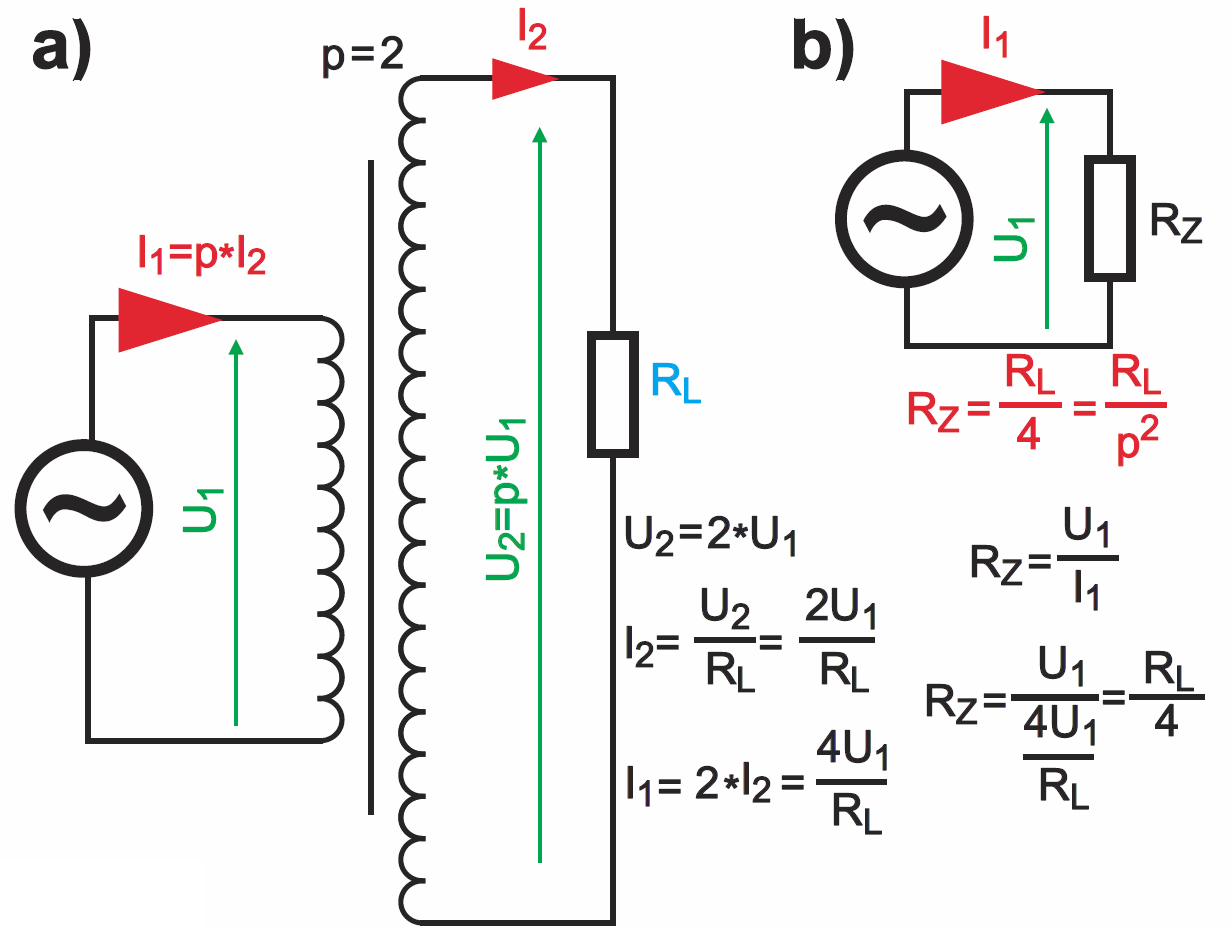
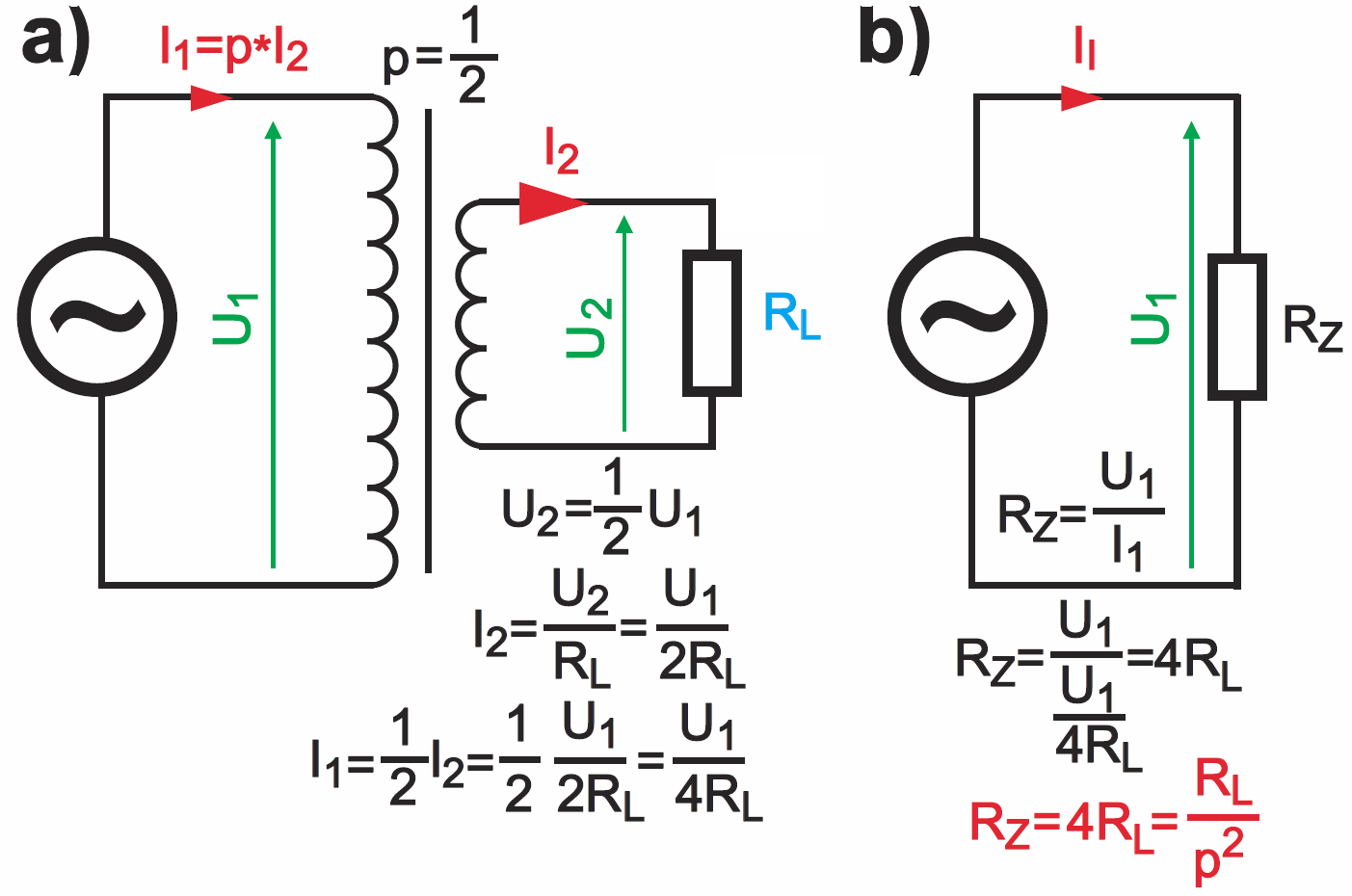
Warto to poczuć i ująć intuicyjnie. Dwa przypadki zilustrowane są na rysunku 8 oraz rysunku 9. Zwróć uwagę na wartości prądów. Gdy transformator ma przekładnię p>1, czyli gdy jest to transformator podwyższający napięcie, to rezystancja zastępcza R_Z jest p² razy mniejsza od rezystancji obciążenia R_L. Natomiast w obwodzie z transformatorem obniżającym napięcie p<1 rezystancja zastępcza R_Z jest 1/p² razy większa od rezystancji obciążenia R_L.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W przypadku transformatorów zasilających, dołączonych do sieci 230 V przedstawionych na fotografii 10 ta „rezystancyjna” zależność nas wcale nie interesuje. Napięcie wejściowe jest niezmienne (230 V) i w ogóle nie mówimy wtedy o przekładni i opornościach, tylko interesuje nas napięcie wyjściowe U₂ i moc maksymalna, której na razie nie omawiamy.

Omawiana „kwadratowa zależność rezystancyjna” jest natomiast przydatna do obliczeń w obwodach akustycznych, gdzie też pracują transformatory. Obliczanie transformatorów wyjściowych do lampowych wzmacniaczy audio to wyższa szkoła jazdy, więc rozważmy łatwiejsze przypadki i to w sposób uproszczony. Dobrym przykładem może być podwyższający transformatorek mikrofonowy – fotografia 11.

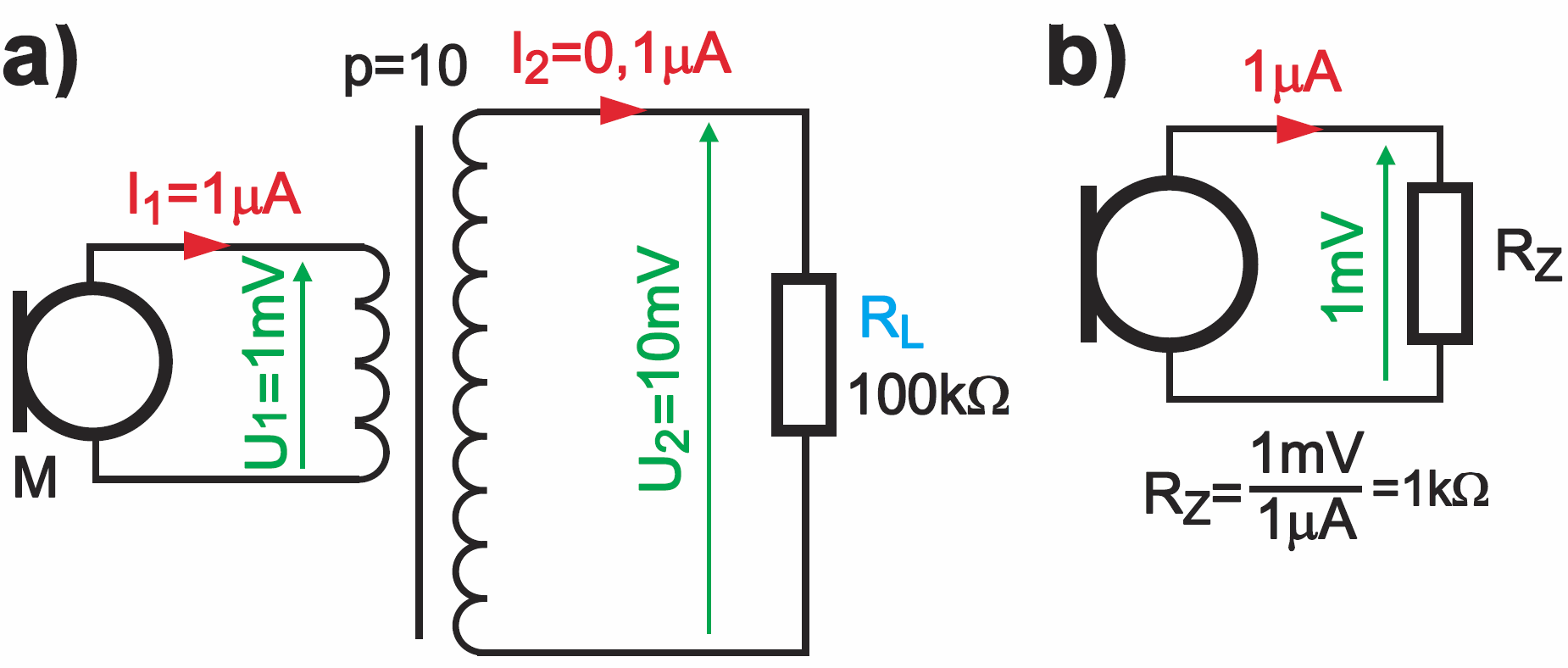
Użycie takiego transformatorka podwyższa napięcie sygnału z mikrofonu (a przy okazji pozwala w prosty sposób zrealizować niskoszumny wzmacniacz, ale to oddzielny, szeroki temat). W idealnym przypadku mikrofon „widzi” ten transformator podwyższający o przekładni p=10, obciążony rezystancją 100 kΩ, jako oporność R_Z=1 kΩ – rysunek 12.

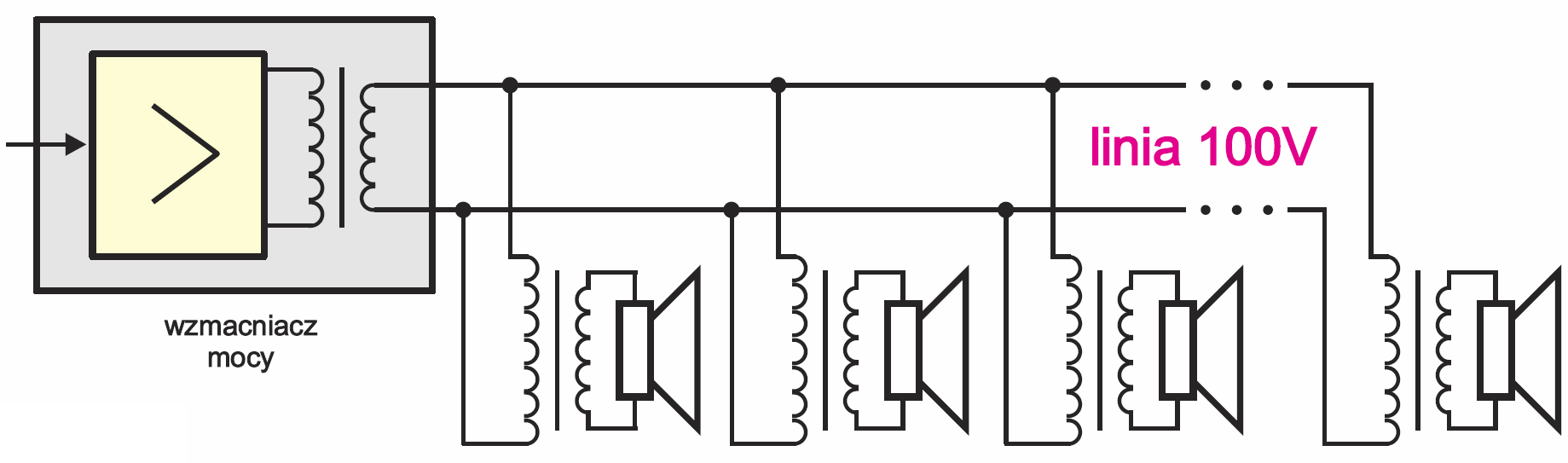
Innym przykładem jest system nagłośnienia z linią radiowęzłową, tzw. 100-woltową. W warunkach nominalnych na tej linii występuje sygnał audio o napięciu aż 100 V. Do takiej linii jest dołączonych wiele małych głośników, które nagłaśniają duży obszar albo szereg pomieszczeń. Z uwagi na wysokie napięcie w linii albo musiałyby to być głośniki o dużej oporności, albo trzeba zastosować transformatory – rysunek 13.

Dzięki transformatorom wzmacniacz i linia „widzą” poszczególne głośniki „przez kwadrat przekładni transformatora”, a to oznacza, że pomimo jednakowej oporności głośników (8 Ω), do każdego może zostać dostarczona inna moc, zależnie od przekładni, jak ilustruje to rysunek 14.

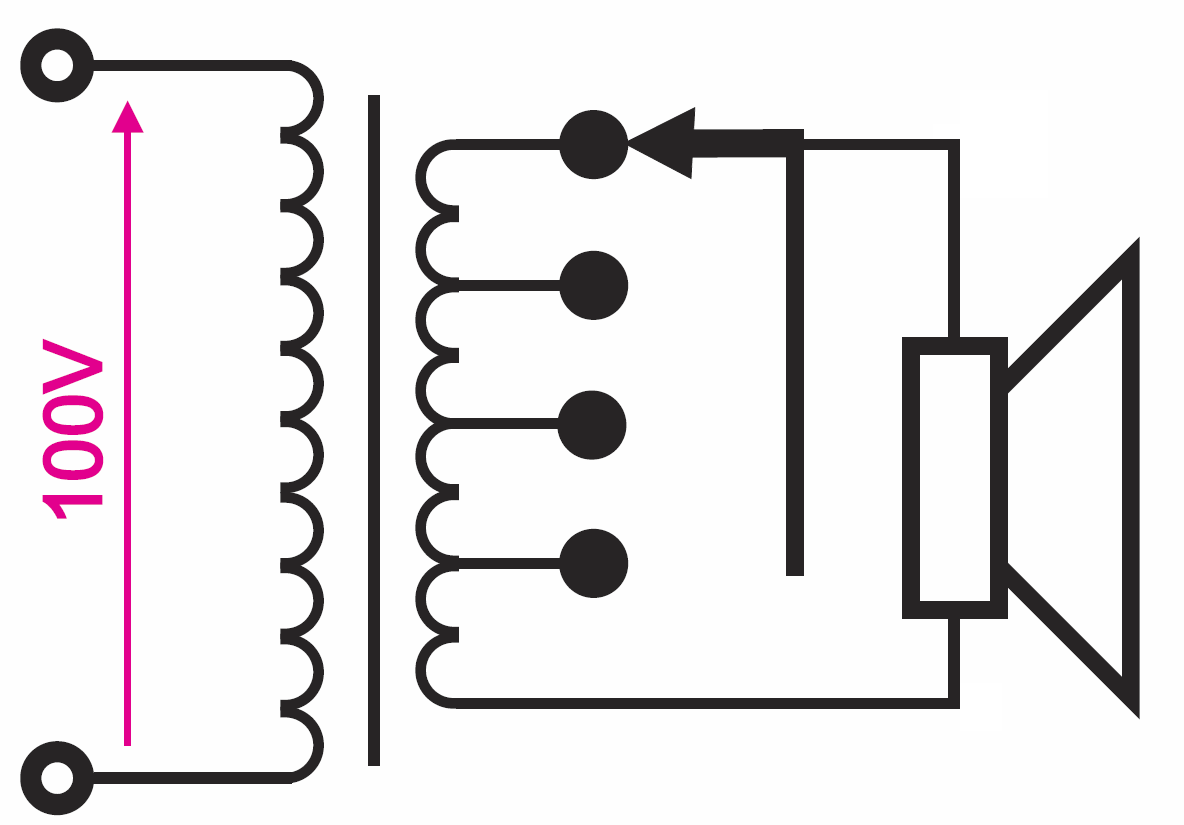
W praktyce realizuje się takie transformatory głośnikowe z odczepami, pozwalającymi skokowo regulować moc dostarczaną do głośnika – rysunek 15.

Zamiast jednak podawać przekładnię, producenci od razu podają przy odczepach moc w standardowych warunkach przy linii 100 V i głośniku 8 Ω, jak pokazuje przykład z fotografii 16 (gdzie także przewidziano współpracę z linią 50-woltową).

I oto w najprostszy sposób omówiliśmy elementarne właściwości idealnego transformatora. Jeszcze raz podkreślam, że wcale nie były do tego potrzebne wiadomości o cewkach, przesunięciach fazowych czy reaktancjach. W idealnym transformatorze istotny jest tylko jeden parametr – przekładnia p. Żadne inne, jak częstotliwość, indukcyjność, moc, nie mają znaczenia.

Zupełnie początkującym wystarczy takie bardzo uproszczone podejście do transformatorów. Jednak rzeczywiste transformatory mają ograniczoną moc, niedoskonałą sprawność i mogą pracować tylko w ograniczonym zakresie częstotliwości. Żeby zrozumieć takie ograniczenia, trzeba dokładniej zapoznać się z transformatorem. Zajmiemy się tym w następnym odcinku.

Piotr Górecki