Elektronika (nie tylko) dla informatyków (27) Transformator idealny – napięcie samoindukcji

W poprzednim odcinku omówiliśmy ogólnie transformator idealny, dzięki któremu mogliśmy zrozumieć uproszczoną zasadę jego działania. W tym wykładzie przypomnimy sobie zjawisko napięcia samoindukcji, które okaże się niezbędne do zrozumienia dalszych rozważań w cyklu dotyczącym transformatorów.

Transformator o skończonej indukcyjności

Do tej pory zakładaliśmy, że uzwojenia transformatora, a przynajmniej uzwojenie pierwotne, ma nieskończenie wielką indukcyjność, co uprościło rozważania, ale nie pozwoliło uchwycić rzeczywistej zasady pracy transformatora. Okazuje się, że transformator o ograniczonej indukcyjności uzwojeń też może być transformatorem idealnym, byle tylko uzwojenia te miały zerową rezystancję. Dopiero rozpatrzenie takiego transformatora bez strat, ale o ograniczonej indukcyjności uzwojeń, pozwoli w pełni zrozumieć zasadę działania transformatora. Początkujący mają problemy ze zrozumieniem tych zagadnień, jeżeli nie poukładają sobie w głowie najbardziej podstawowych wiadomości. Częsty błąd polega na tym, że szukają oni związku napięcia wejściowego z wyjściowym bez należytego zrozumienia roli prądu i strumienia magnetycznego.

My dla uproszczenia rozważmy najpierw stan jałowy transformatora o skończonej indukcyjności. Żeby ułatwić analizę, niech to będzie transformator sieciowy, czyli taki dołączony do sieci energetycznej 230 V. Wtedy do źródła napięcia sinusoidalnego o niezmiennym napięciu 230 V podłączone jest uzwojenie pierwotne, a uzwojenie wtórne nie jest nigdzie podłączone i tak naprawdę transformator zachowuje się jak zwyczajna cewka z dodatkowym, nieczynnym uzwojeniem wtórnym. Warto najpierw dokładniej rozważyć zjawiska zachodzące w tak pracującej zwykłej cewce, a dopiero potem przejść do transformatora.

Napięcie, prąd, strumień, napięcie…

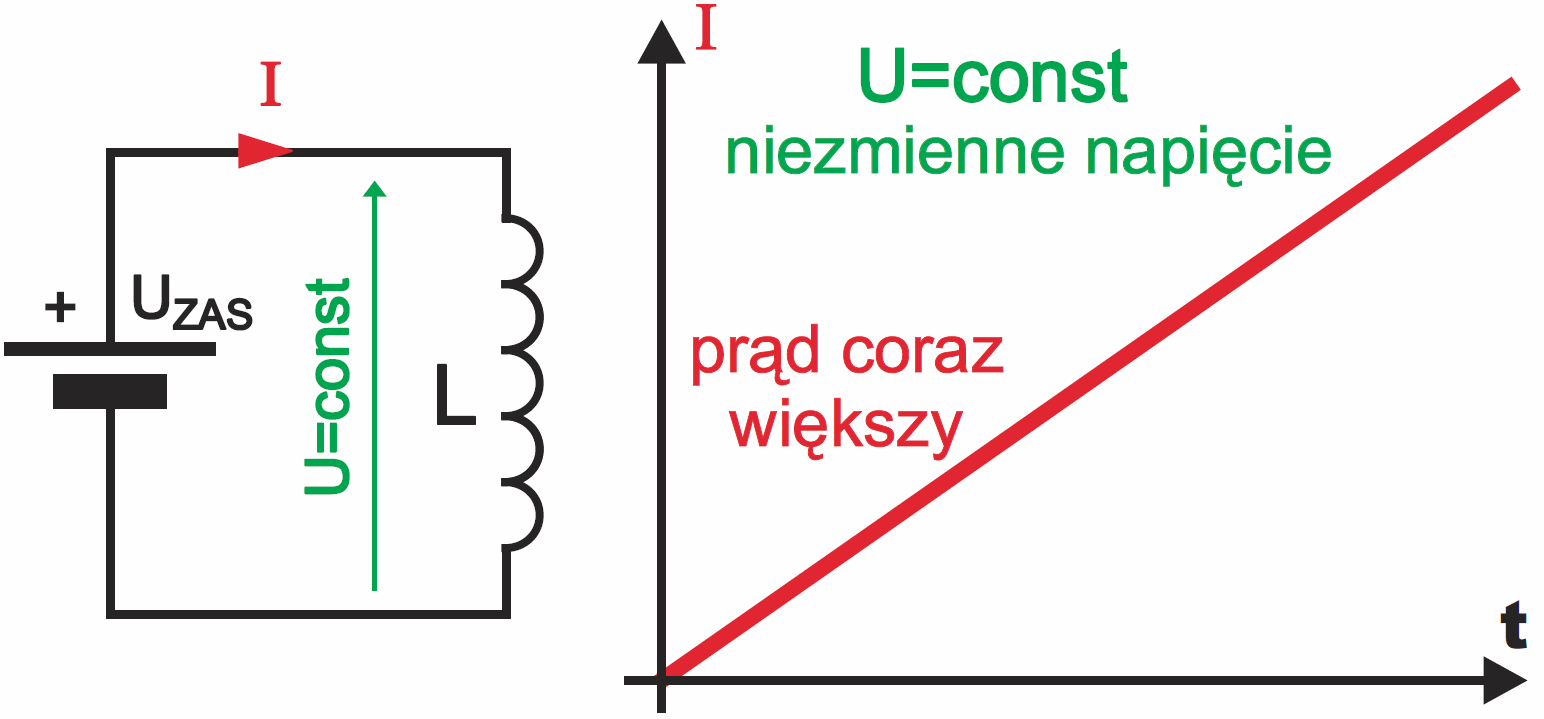
Przy omawianiu cewek już wspomnieliśmy o zjawisku „samopilnowania”. Musimy do tego wrócić. W obwodzie z rysunku 1 mamy źródło napięcia stałego U_ZAS, a cewka jest idealna, więc nie ma rezystancji ograniczającej prąd. Dlaczego więc po zamknięciu obwodu przez cewkę nie zaczyna natychmiast płynąć ogromny prąd? Co jest czynnikiem hamującym?

Tym czynnikiem hamującym nie jest rezystancja, która w przypadku cewki idealnej jest równa zeru. Już wcześniej stwierdziliśmy, że zmiany prądu płynącego w cewce powodują powstanie napięcia samoindukcji, którego wartość (SEM) jest wprost proporcjonalna do szybkości zmian prądu, co możemy zapisać SEM = dI/dt (w uproszczeniu SEM = ΔI/Δt). Wiemy, że czynnikiem hamującym i wyznaczającym szybkość narastania prądu jest więc napięcie samoindukcji SEM, które odejmuje się od napięcia zasilającego (kompensuje napięcie zasilające). Prąd rośnie z dokładnie taką szybkością, żeby wytworzone napięcie (SEM) było równe napięciu zasilania U_zas, czyli żeby różnica między tymi napięciami była… równa zeru. Jeśliby prąd rósł wolniej, to wytworzona wartość SEM byłaby mniejsza od U_ZAS i różnica tych napięć natychmiast spowodowałaby wzrost szybkości narastania prądu, by doprowadzić do równości SEM=U_ZAS. Analogicznie zbyt duża wartość prądu spowodowałaby wytworzenie zbyt dużego napięcia SEM, co zahamowałoby szybkość narastania prądu.

W cewce podłączonej do napięcia stałego mamy więc do czynienia ze swego rodzaju autoregulacją, „samopilnowaniem” – szybkość narastania prądu i wytwarzane napięcie SEM „pilnują się wzajemnie”. Ale to pilnowanie wiąże tylko szybkość narastania prądu z napięciem, a nie ogranicza wartości prądu – w obwodzie prądu stałego prąd narasta liniowo, teoretycznie aż do nieskończoności, jak pokazuje rysunek 1.

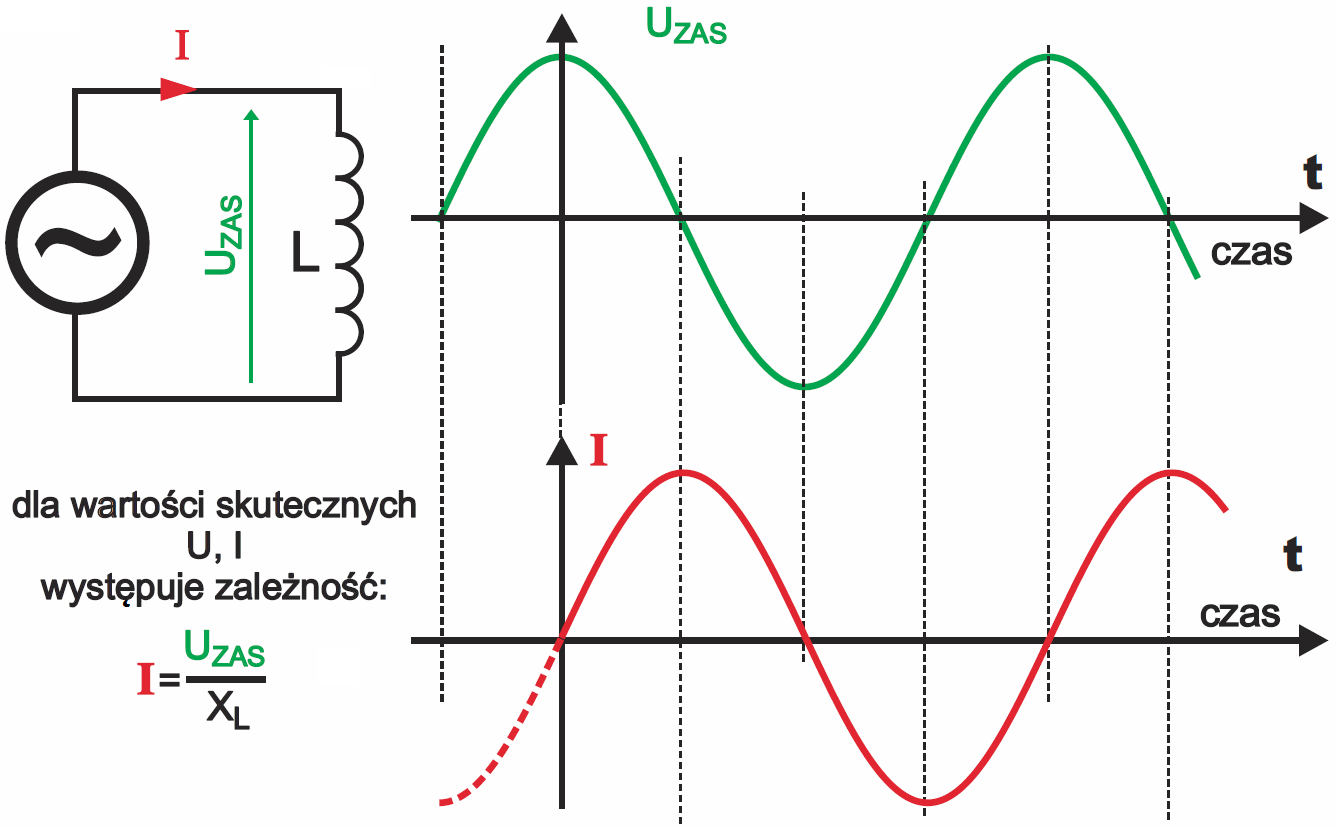
Z wcześniejszych rozważań wiemy, że w przypadku dołączenia cewki do źródła napięcia zmiennego, szybkość i kierunek zmian prądu są wyznaczone przez chwilową wartość i biegunowość napięcia na cewce. Co dla nas teraz najważniejsze, istnieje jeden przypadek szczególny: otóż w przypadku dołączenia cewki do źródła napięcia sinusoidalnego, prąd też jest sinusoidalny, jak ilustruje to rysunek 2. Już wcześniej podkreślałem, że podstawowa zasada jest ta sama dla prądu stałego i zmiennego: podanie napięcia na cewkę powoduje zmiany płynącego przez nią prądu, a to skutkuje powstaniem napięcia samoindukcji.

Teraz dla zrozumienia zasady działania transformatora, trzeba dokładniej przyjrzeć się napięciu samoindukcji i rozważyć następującą sekwencję przyczynowo-skutkową:

napięcie zasilania → prąd w cewce → strumień magnetyczny → napięcie samoindukcji.

Otóż dołączenie do cewki napięcia powoduje przepływ przez nią prądu. Ten prąd, przepływając przez cewkę, spowoduje wytworzenie pola magnetycznego, a konkretnie strumienia magnetycznego, ściślej strumienia indukcji magnetycznej. Zapamiętaj: przepływ prądu przez cewkę powoduje powstanie strumienia magnetycznego.

Nie musisz rozumieć ze wszystkimi szczegółami, czym jest pole magnetyczne, strumień indukcji magnetycznej, oznaczany Φ, czy natężenie pola magnetycznego, oznaczane H i indukcja magnetyczna, oznaczana literą B. Ścisłe definicje tych pojęć i wielkości są naprawdę skomplikowane, o czym możesz się przekonać choćby w Wikipedii. Na razie radykalnie uprośćmy zagadnienie: zapewne pamiętasz ze szkolnych lekcji lub podręczników fizyki doświadczenie z magnesem i opiłkami żelaza – opiłki żelaza tworzą wokół magnesu swego rodzaju linie, pętle – fotografia 3 (z Wikipedii).

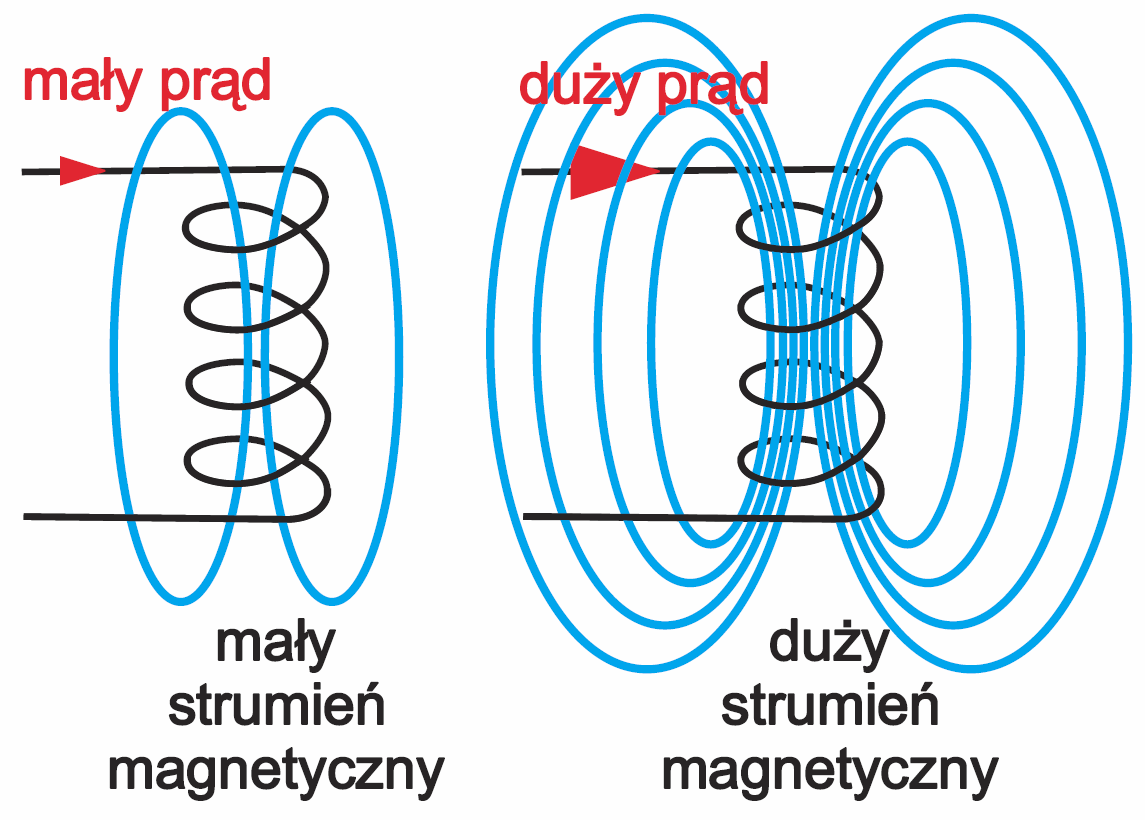
Możemy sobie wyobrażać, że czym silniejszy magnes, tym więcej jest tych linii. Przy przepływie prądu przez cewkę tworzy się elektromagnes i też występują takie linie pola magnetycznego. Śmiało możemy uważać, że strumień magnetyczny to liczba linii sił pola magnetycznego. W pierwszym przybliżeniu możemy też przyjąć, że strumień jest wprost proporcjonalny do prądu płynącego przez cewkę. Czym większy prąd, tym większy strumień – rysunek 4.

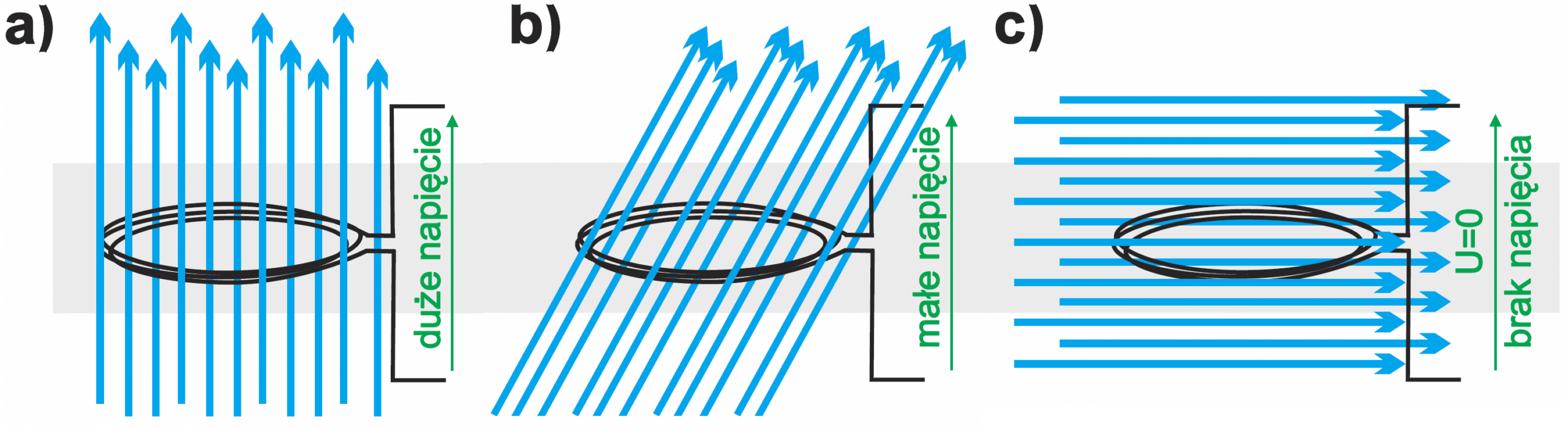
Żebyśmy nie zgubili obrazu całości, podkreślam, że w zasadzie w cewce i transformatorze „pierwotną przyczyną” jest napięcie U_zas. Napięcie to powoduje przepływ przez cewkę prądu. Przepływ prądu przez cewkę powoduje powstanie strumienia magnetycznego. I tu w grę wchodzi kolejne ważne zjawisko: zjawisko indukcji elektromagnetycznej, odkryte w roku 1831 przez M. Faradaya. Otóż zmiany strumienia magnetycznego powodują indukowanie się napięcia w przewodniku umieszczonym w tym zmiennym polu magnetycznym. Napięcie to bywa też nazywane siłą elektromotoryczną i oznaczane SEM. Podkreślam, że napięcie jest wytwarzane nie pod wpływem obecności strumienia magnetycznego, tylko pod wpływem zmian strumienia magnetycznego (lub ruchu przewodnika w tym polu, ale to inny przypadek). Jeśli nie ma zmian strumienia magnetycznego, to nie indukuje się napięcie. W zasadzie zmiany strumienia indukują napięcie w każdym przewodniku, ale nas interesuje indukowanie napięcia w zwoju, a właściwie w wielu zwojach. Nie wchodząc w szczegóły, możemy powiedzieć, że zwój w pełni wykorzystuje strumień magnetyczny, jeżeli linie pola magnetycznego są prostopadłe po płaszczyzny zwoju. Gdy linie pola tworzą z płaszczyzną zwoju kąt inny niż prosty, „stopień wykorzystania” jest mniejszy. W skrajnym przypadku, gdy linie pola są równoległe do płaszczyzny zwoju, zmiany tego pola nie indukują żadnego napięcia. Ilustruje to rysunek 5. Ma to duże znaczenie praktyczne, ale nie będziemy wchodzić w szczegóły. W cewce i w transformatorze linie pola są prostopadłe do powierzchni zwojów, według rysunku 5a.

I oto mamy tu pełniejsze wyjaśnienie omawianej wcześniej samoindukcji w cewce: to zmieniający się strumień magnetyczny powoduje powstanie napięcia w każdym zwoju cewki. Powstające napięcie SEM jest wprost proporcjonalne właśnie do szybkości zmian strumienia magnetycznego, ale strumień zależy od prądu, dlatego SEM jest wyznaczona przez szybkość zmian prądu (SEM ≈ dI/dt). Zgodnie z regułą przekory Lenza, tak indukowane napięcie (siła elektromotoryczna SEM) będzie się odejmować od napięcia zasilającego U_ZAS i podczas normalnej pracy cewki/transformatora wypadkowa tych obydwu napięć będzie równa zeru, czy też bardzo bliska zeru, żeby zapewnić przepływ przez cewkę prądu o potrzebnej wartości.

To jest proste, ale może znów nasunie Ci się pytanie: a skąd cewka wie, jak duże ma być to indukowane napięcie SEM i „prąd o potrzebnej wartości”? Otóż cewka nie musi niczego wiedzieć: gdyby sinusoidalny prąd i powstający sinusoidalny strumień były za małe, to powstające sinusoidalne napięcie samoindukcji SEM byłoby zbyt małe i nie skompensowałoby napięcia zasilania. Wtedy różnica napięć spowodowałaby wzrost prądu, a tym samym szybkości zmian prądu i strumienia do takiej wartości, by dokładnie skompensować napięcie zasilające.

Omawiane zasady dotyczą napięć wejściowych o dowolnym kształcie. Co ważne, podanie na cewkę napięcia sinusoidalnego spowoduje przepływ przez nią sinusoidalnego prądu, przesuniętego o jedną czwartą okresu (rysunek 2). Podobnie sinusoidalny kształt ma też przebieg zmian strumienia magnetycznego. W tym szczególnym przypadku sinusoidalnego napięcia zasilającego możemy mówić o oporności: przy częstotliwości f cewka o indukcyjności L przedstawia sobą oporność, reaktancję indukcyjną X_L, o wartości: X_L = 2πfL Oznacza to, że napięcie U_ZAS powoduje przepływ przez cewkę prądu o wartości wyznaczonej przez reaktancję indukcyjną X_L: I = U_ZAS/X_L

Przy przebiegach o innych kształtach, niż sinusoidalny takich obliczeń nie można wykonywać, bo nie mają one sensu.

A teraz jeszcze inny aspekt zagadnienia: w idealnej cewce nie występują straty. Oznacza to, że płynący prąd sinusoidalny w jednej części okresu przenosi energię ze źródła zasilania do cewki (ładuje cewkę), a po chwili, w drugiej części okresu, prąd ten przenosi tę energię w przeciwnym kierunku – z cewki z powrotem do źródła zasilania. I tak jest w każdym cyklu przebiegu zmiennego. W przypadku idealnym mamy więc jedynie do czynienia z cyklicznym przekazywaniem energii między źródłem a cewką raz w jedną, raz w drugą stronę, bez żadnych strat. Przy przebiegu o częstotliwości 50 Hz, taka cykliczna wymiana energii następuje 50 razy na sekundę.

I oto mamy wszelkie informacje, potrzebne do analizy stanu jałowego transformatora, bo transformator w stanie jałowym to po prostu cewka z dodatkowym, niepodłączonym uzwojeniem.

Zajmiemy się tym w następnym odcinku.

Piotr Górecki