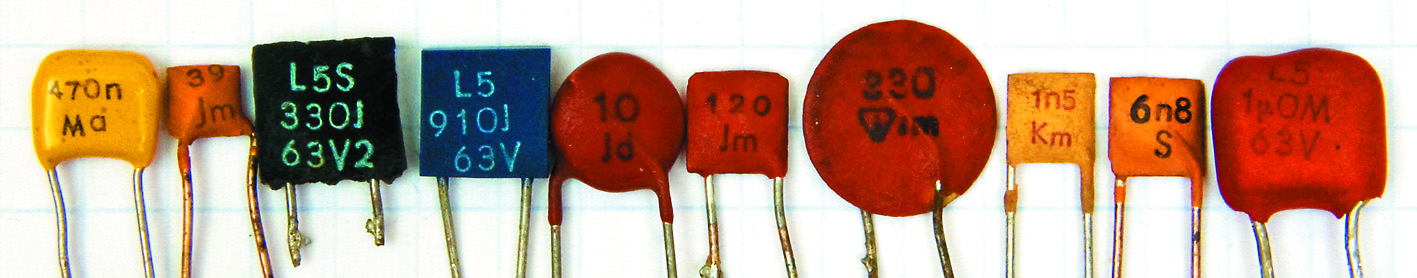
Elektronika (nie tylko) dla informatyków (38) Kondensatory ceramiczne – zależność pojemności od innych czynników

W poprzednim odcinku analizowaliśmy bardziej szczegółowo współczynnik cieplny różnych dielektryków stosowanych w kondensatorach ceramicznych. W tym odcinku omówimy inne czynniki od których zależy w mniejszym lub w większym stopniu pojemność kondensatora.

W poprzednim odcinku zasygnalizowałem, że w oznaczeniu EIA kondensatorów ferroelektrycznych trzeci znak w oznaczeniu to nie jest tolerancja, która jest rozumiana jako odchyłka od wartości nominalnej „w spoczynku”.

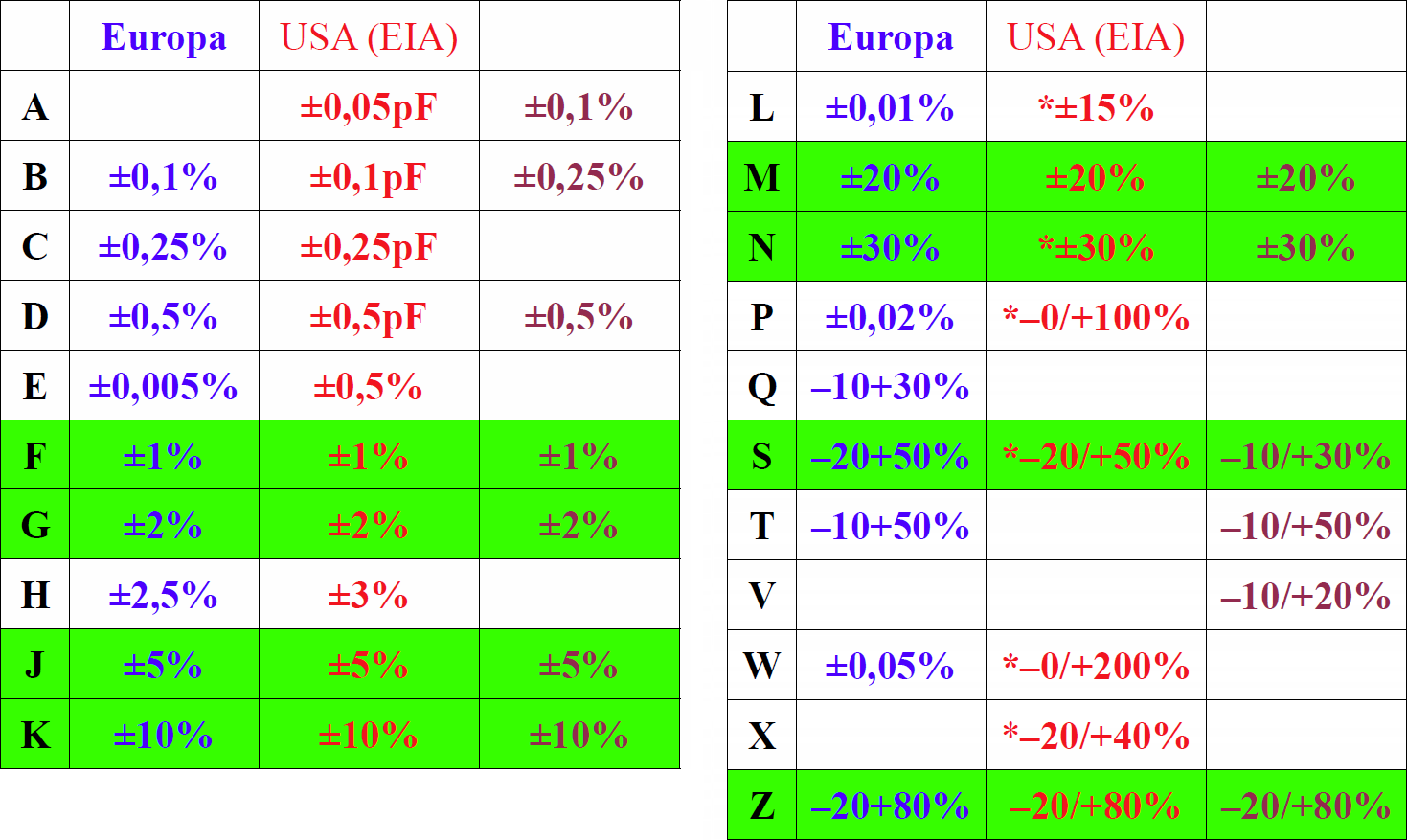
Otóż „tolerancja spoczynkowa” zwykle oznaczana jest za pomocą oddzielnej, dodatkowej litery. Jest tu jednak pewien kłopot, bo oznaczenia nie są jednakowe. Na rysunku 1 w formię tabeli kolorem niebieskim podane jest znaczenie liter według norm europejskich. Ale niektórzy producenci stosują też inne kody, gdzie poszczególne litery mają inne znaczenie. Kolorem czerwonym podane są oznaczenia według amerykańskiego stowarzyszenia EIA, spośród których te wyróżnione gwiazdką nie są przyjęte przez ogół tamtejszych producentów. W trzeciej kolumnie podane są oznaczenia stosowane przez pewną znaną firmę. Zielonym tłem wyróżnione są wartości wspólne.

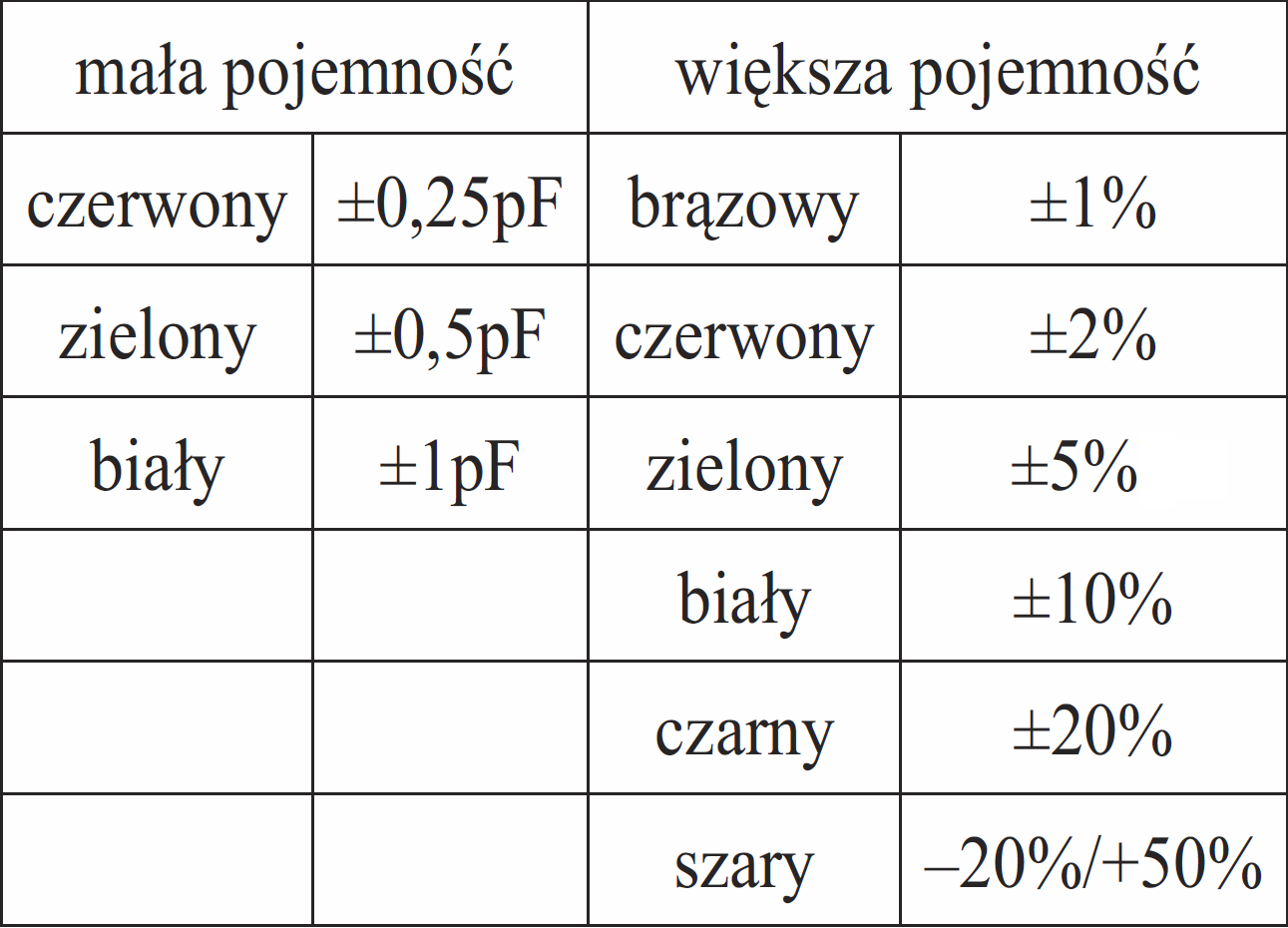
Według niektórych firm, litery B, C, D dla pojemności do 10 pF oznaczają tolerancję w pikofaradach, a dla kondensatorów >10 pF taką samą liczbową wartość w procentach. Inne źródła podają, że tolerancja bywa też oznaczana za pomocą kolorowej kropki lub paska według poniższego zestawienia, tabeli przedstawionej na rysunku 2.

W praktyce często mamy do czynienia z kondensatorami o tolerancji, oznaczonej literami J, K, M, S (5%, 10% i 20%, – 20%/+50%) – fotografia 3, rzadko z literami F, G (1%, 2%).

W przypadku kondensatorów klasy 1 sprawa tolerancji jest jasna. Przykładowo kondensator C0G (NP0) 1000 pF może mieć tolerancję, np. 5% (±5%), oznaczoną literą J, czyli „wartość spoczynkowa” może będzie wynosić od 950…1050 pF. Pod wpływem temperatury pojemność zmieni się tylko o ułamek procenta, o mniej niż 10 pF. Tu nie ma wątpliwości.

W przypadku kondensatorów ferroelektrycznych zagadnienie jest bardziej złożone. Jeślibyśmy zmierzyli ich pojemność w „warunkach standardowych”, czyli w temperaturze pokojowej i bez polaryzującego napięcia stałego, to rozrzut wartości elementów okaże się niezbyt duży, na przykład ±10% (K), ±20% (M) czy –20…+50% (S). Jednak pod wpływem temperatury i przyłożonego napięcia (stałego) pojemność kondensatora ferroelektrycznego może zmienić się o dużo więcej, niż wynosi jego tolerancja.

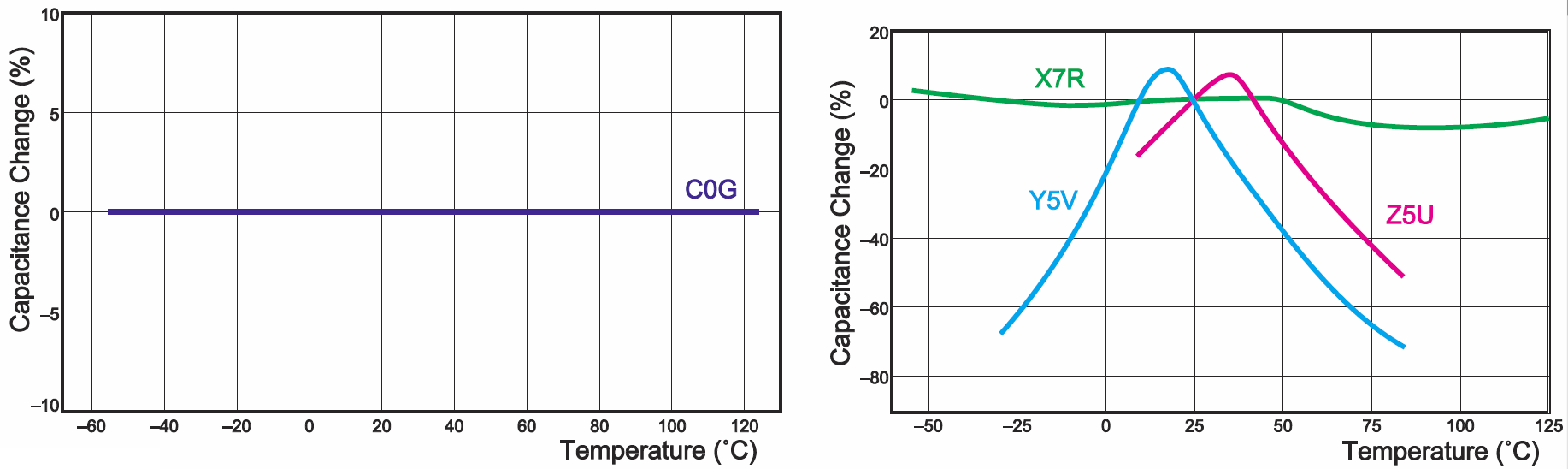
Co ważne, w przypadku niestabilnych kondensatorów ferroelektrycznych nie można mówić o współczynniku cieplnym, ponieważ zmiany pojemności są ogromne i nieliniowe. Rysunek 4 pokazuje porównanie zależności temperaturowych popularnych kondensatorów C0G, X7R, Y5V, Z5U.

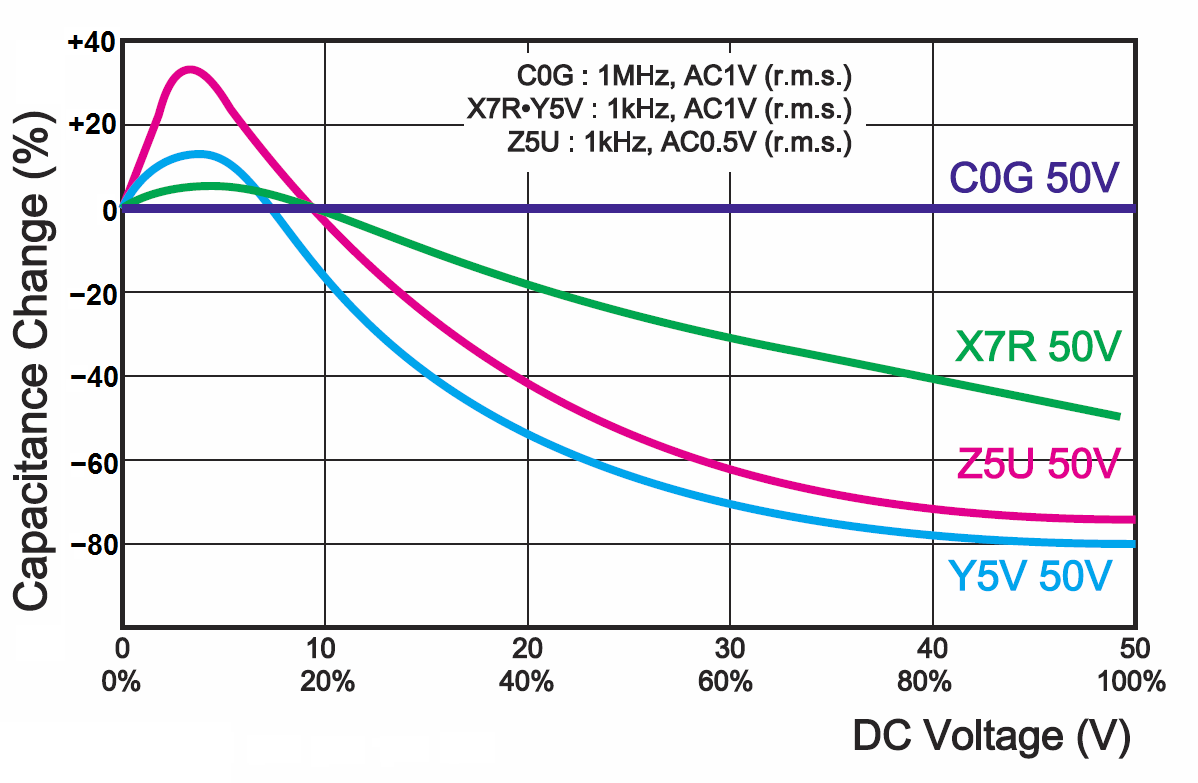
Jak widać, te ostatnie zachowują dużą (nominalną) pojemność tylko w zakresie temperatur pokojowych, a i przy wzroście, i przy zmniejszaniu temperatury, pojemność zdecydowanie maleje. Z kolei rysunek 5 pokazuje zależność pojemności od napięcia stałego, występującego na okładkach. „Prawdziwy” kondensator C0G w ogóle nie reaguje na polaryzujące napięcie stałe. Natomiast ceramika ferroelektryczna traci przenikalność i pojemność drastycznie maleje. Na rysunku 5 pokazane są bezwzględne wartości napięcia w woltach dla kondensatorów o napięciu nominalnym 50 V, ale dodatkowo zamieszczona jest też skala procentowa. Aby zmiany pojemności nie były tak duże, można zastosować kondensatory o wyższym napięciu nominalnym.

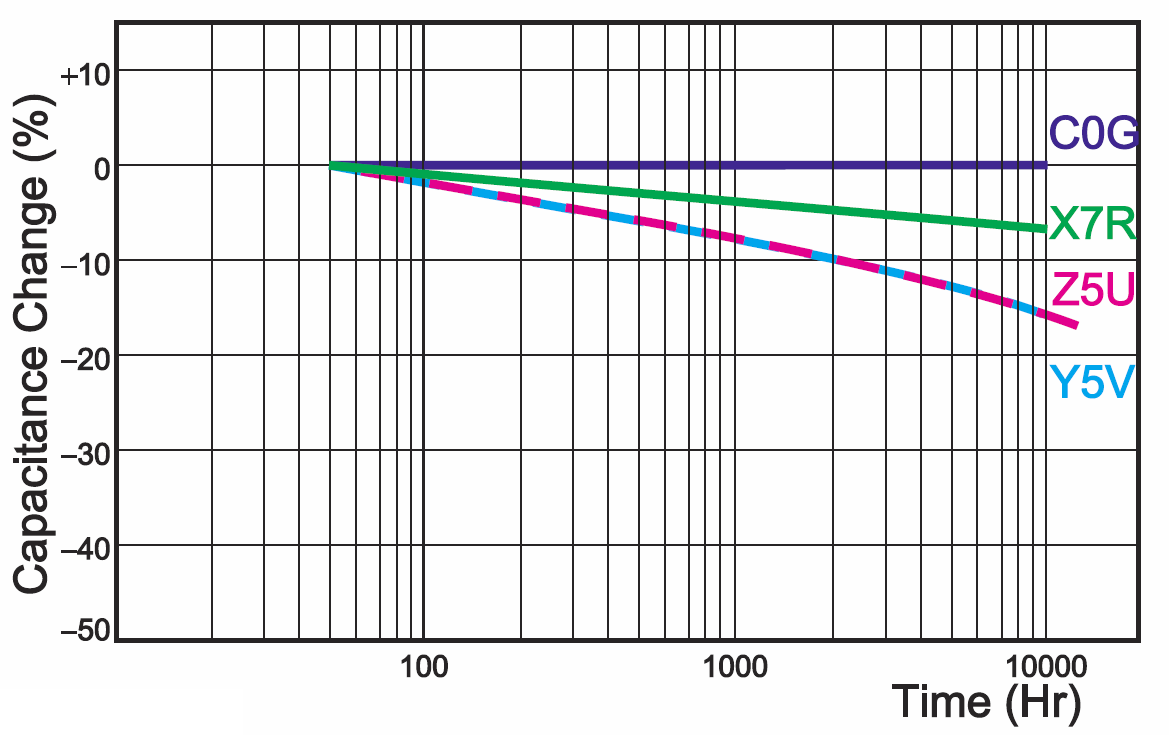
To nie koniec problemów: rysunek 6 pokazuje problem starzenia. Znów kondensatory C0G okazują się znakomite. Natomiast w ferroelektrycznych występuje logarytmiczna zależność utraty pojemności, dlatego nie podaje się utraty pojemności na rok, tylko utratę pojemności w procentach na dekadę, czyli przy dziesięciokrotnym zwiększeniu czasu. Rysunek wskazuje, iż ferroelektryki o najwyższej przenikalności mogą utracić do 15% swej pojemności po 10000 godzinach czyli po roku i dwóch miesiącach. Trzy ostatnie rysunki pochodzą z katalogów renomowanej firmy MuRata. Kondensatory ferroelektryczne innych producentów mogą mieć znacząco gorsze parametry. Na przykład spotyka się informacje, że kondensatory X7R i X5R wykazują utratę pojemności 1,5…4% na dekadę, natomiast typu Z5U czy Y5V nawet 5…10%/dekadę.

Wszystkie te informacje świadczą, że kondensatory ferroelektryczne typu 2 i 3 nie nadają się do żadnych zastosowań, wymagających stabilności. W takich zastosowaniach mogą pracować tylko kondensatory ceramiczne typu 1, w praktyce C0G (NP0). Jednak to głównie kondensatory ferroelektryczne są produkowane w miliardach egzemplarzy na rok. Są one powszechnie używane w obwodach zasilania jako kondensatory odsprzęgające, filtrujące zasilanie, a często także jako kondensatory sprzęgające, których zadaniem jest przepuścić sygnały zmienne, a oddzielić składową stałą. Współczesny laptop czy odbiornik telewizyjny zawiera mniej więcej 700…1000 sztuk kondensatorów ceramicznych, oczywiście w wersji SMD.

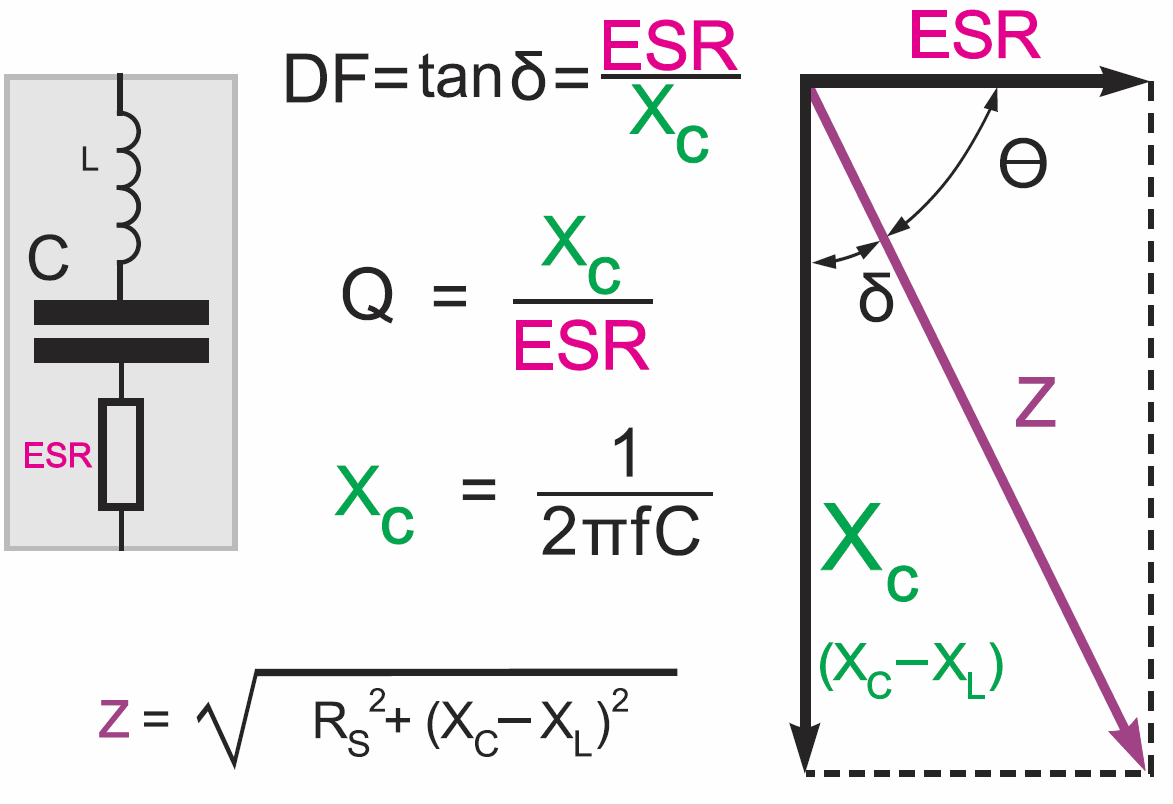
Oprócz wspomnianych wad, związanych z niestabilnością parametrów, w kondensorach ferroelektrycznych znaczący jest też problem strat. Problem strat w dielektryku występuje we wszystkich rzeczywistych kondensatorach. Jednak można uznać, że w kondensatach typu 1 straty te są bardzo małe, dobroć – bardzo duża, co w większości zastosowań pozwala zapomnieć o problemie. Natomiast w kondensatorach ferroelektrycznych straty są kilkadziesiąt razy większe. Przy zmianach naelektryzowania ferroelektryka znacząca część energii elektrycznej zamienia się na ciepło. Przy przebiegach zmiennych kondensator zachowuje się tak, jakby zawierał w środku dodatkową rezystancję. Dodatkowego wbudowanego opornika tam nie ma, ale występują straty ciepła w dielektryku, co zwykle przedstawiane jest jako zastępcza rezystancja szeregowa ESR. Oprócz niepożądanej rezystancji strat, w kondensatorze występuje też pasożytnicza indukcyjność, związana z budową kondensatora, zwłaszcza z długością jego wyprowadzeń. W rezultacie schemat zastępczy kondensatora zazwyczaj przedstawiany jest tak, jak na rysunku 7. Wypadkowa reaktancja jest różnicą między reaktancją pojemnościową X_C i reaktancją indukcyjną X_L, a w związku z przesunięciem fazy, impedancję Z, czyli oporność całkowitą, przedstawia się jako wielkość wektorową.

W praktyce straty można charakteryzować na kilka sposobów. Można np. podać wartość rezystancji zastępczej ESR. Można podać wartość dobroci Q, która jest stosunkiem reaktancji X do rezystancji ESR (Q = X / ESR). W przybliżeniu bierze się tu wartość reaktancji pojemnościowej X_C, jednak ściślej biorąc, należałoby wziąć wartość różnicy reaktancji (X = X_C – X_L).

Można wreszcie podać wartość współczynnika strat (DF – Dissipation Factor), który jest jednocześnie tangensem kąta δ. Współczynnik strat DF (tangens δ) to po prostu odwrotność dobroci:
DF = tan δ = 1/Q

Wartość współczynnika strat DF najczęściej podaje się w procentach.

W przypadku kondensatorów typu 1 straty są małe i w katalogach zwykle podaje się wartość dobroci, która jest rzędu 1000, co znaczy, że współczynnik strat jest mały, rzędu 0,1%. W kondensatorach typów 2 i 3, np. X7R i Z5U, współczynnik strat DF jest rzędu, odpowiednio 2,5% i 4%, co znaczy, że ich dobroć Q jest rzędu odpowiednio 40 i 25.

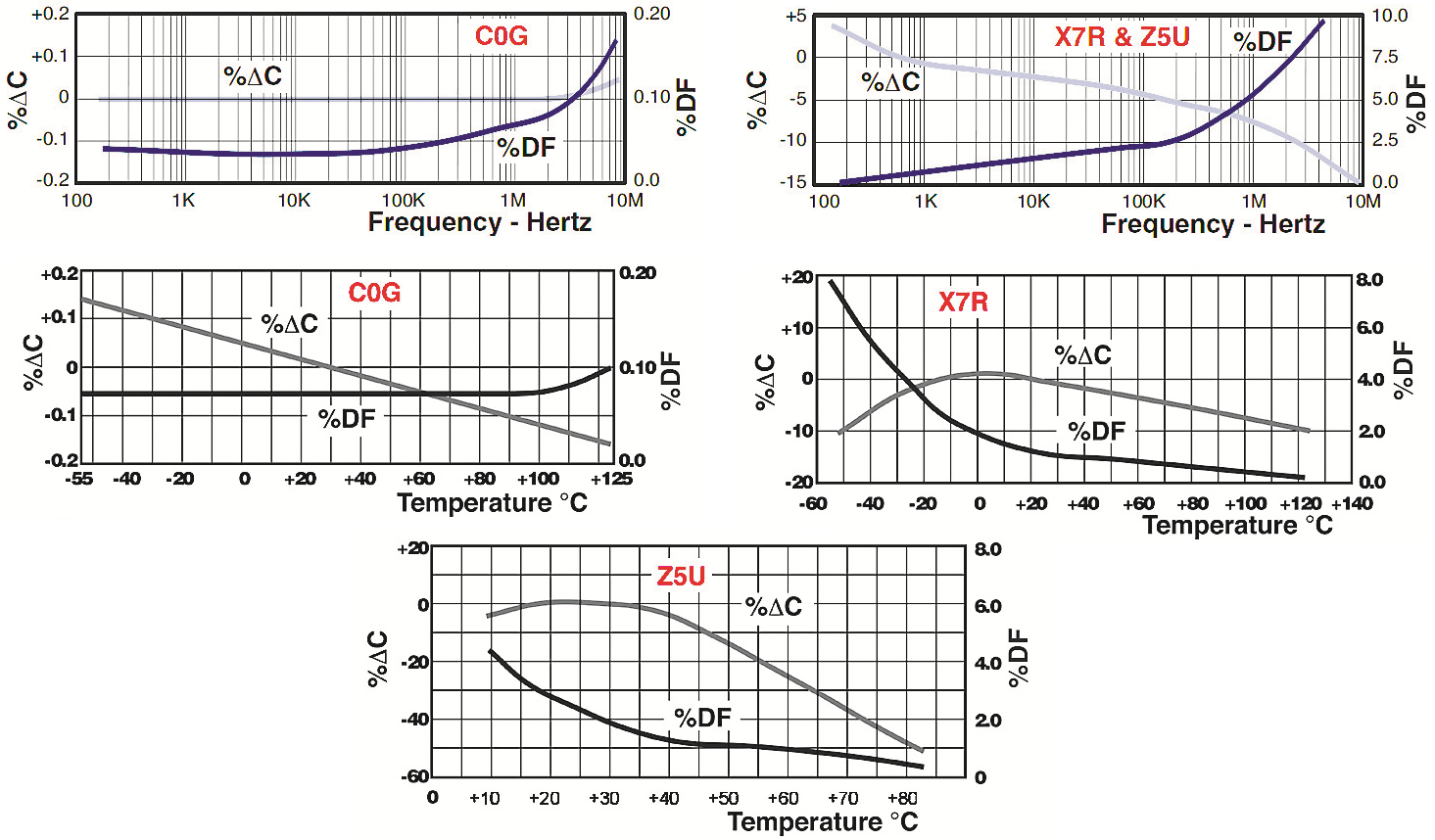
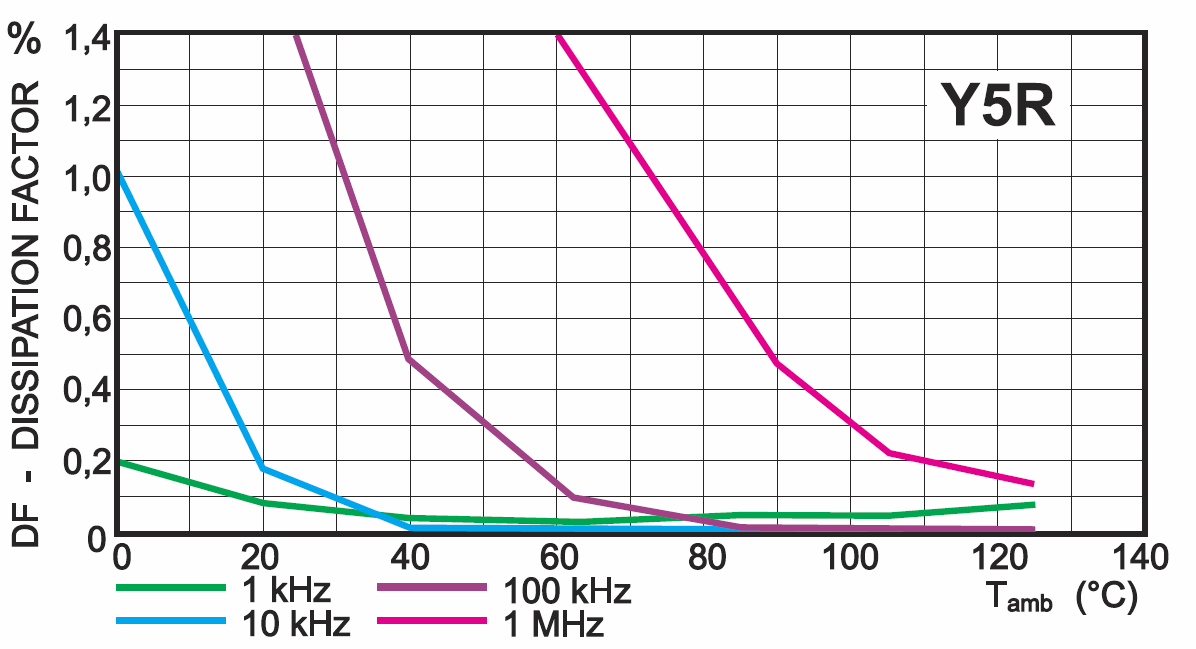
Podana w katalogu wartość współczynnika strat DF nie jest do końca miarodajna. Jest ona zmierzona w określonych warunkach przy jednej częstotliwości (dla C do 1 nF przy f = 1 MHz, dla C>1 nF przy f = 1 kHz). Tymczasem straty zależą od różnych czynników. Rysunek 8 pokazuje zależności współczynnika DF od temperatury i od częstotliwości dla podstawowych rodzajów ceramiki (dodatkowo też zmiany pojemności).

Z kolei rysunek 9 pokazuje zależność strat od temperatury przy różnych częstotliwościach.

Generalnie straty są wadą. Jednak paradoksalnie, znaczna stratność, czyli niezbyt duża dobroć „ferroelektryków” często okazuje się zaletą w obwodach odsprzęgania zasilania, kondensatory takie wchodzą w skład różnych pasożytniczych obwodów RLC. Znacząca rezystancja strat obniża dobroć takich pasożytniczych obwodów, co pozwala łatwiej uporać się z problemami.

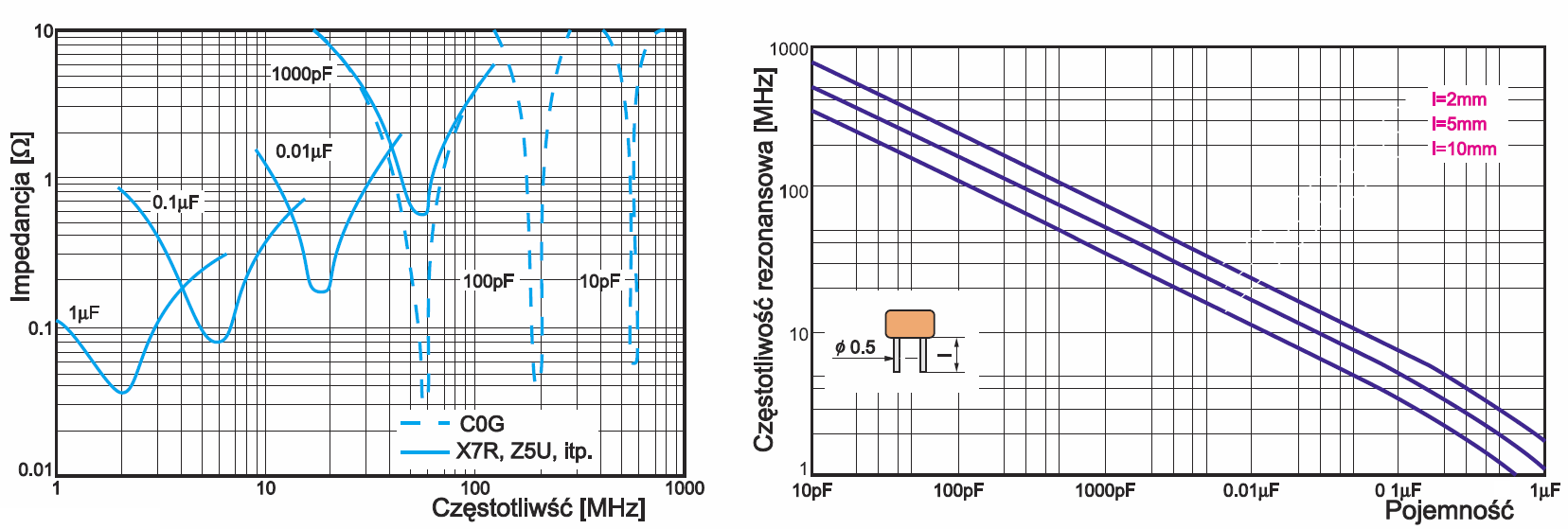
Obecność pasożytniczych indukcyjności powoduje, że każdy kondensator jest w rzeczywistości szeregowym obwodem rezonansowym (rysunek 7). Częstotliwość rezonansu szeregowego, przy której impedancja elementu jest najmniejsza, zależy nie tylko od pojemności kondensatora, ale też od długości wyprowadzeń oraz oczywiście od rezystancji ESR. Rysunek 10 pokazuje te zależności dla kondensatorów firmy MuRata.

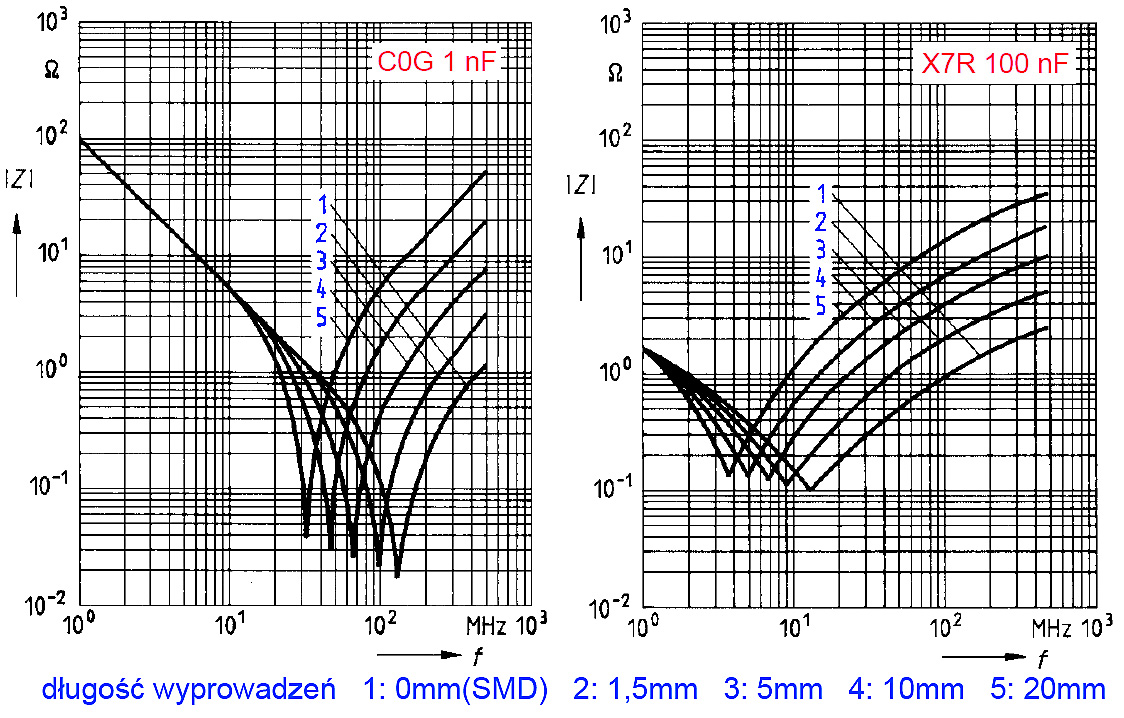
Na lewym wykresie pokazany jest przebieg impedancji w funkcji częstotliwości dla kondensatorów ceramicznych o różnej pojemności. Wykres z prawej strony pokazuje wpływ długości wyprowadzeń na częstotliwość rezonansową. Analogiczne informacje zawiera rysunek 11 (z materiałów Siemens-Matsushita), ilustrujący częstotliwość rezonansową zależnie od długości wyprowadzeń dla konkretnych dwóch kondensatów.

Jak z tego widać, warto minimalizować długość wyprowadzeń, ponieważ właściwości układu w zakresie wysokich częstotliwości będą w znacznym stopniu zależne od długości wyprowadzeń i sposobu montażu, w tym długości ścieżek. Ma to również wpływ na skłonności do samowzbudzenia, wynikające z niedoskonałości obwodów zasilania. Sprawa jest skomplikowana, jednak ogólnie biorąc, najkorzystniejsze właściwości mają kondensatory SMD (fotografia 12), które z natury nie zawierają drutowych wyprowadzeń.

A w następnym odcinku zajmiemy się starymi oznaczeniami kondensatorów.

Piotr Górecki