Poznajemy tranzystory – część 11

W poprzednim odcinku zapoznałeś się z rzeczywistymi modelami tranzystora. W tym odcinku jeszcze raz przypomnę pojęcie czarnej skrzynki, zajmiemy się bowiem parametrami macierzowymi h, budzącymi grozę wielu początkujących. Ten odcinek pozwoli zrozumieć sens parametrów h i ich praktyczną przydatność. Wspólnie wysnujemy też ważne wnioski dotyczące obliczeń teoretycznych.

Ostatnio tłumaczyłem ci, że tranzystor, choć ma tylko trzy nóżki, jest tworem bardzo kapryśnym i wcale nie jest łatwo precyzyjnie opisać jego właściwości. Na twoje i moje szczęście, w praktyce zazwyczaj nie ma potrzeby wnikać we wszystkie szczegóły. Chyba się ze mną zgodzisz, że gdybyśmy musieli od początku analizować wspomniany w poprzednim odcinku model Ebersa−Molla lub jakiś inny, jeszcze bardziej skomplikowany, to na pewno odeszłaby nam ochota na zajmowanie się elektroniką.

Dlatego jeśli to konieczne, zamiast jakichś koszmarnych obliczeń z wykorzystaniem wyższej matematyki (które zresztą przeprowadza każdy program komputerowej symulacji), przyjmujemy modele prostsze, czasem nawet bardzo uproszczone. Takie uproszczone modele pozwalają przeprowadzić obliczenia ze stosunkowo niewielkim błędem. Chyba nie muszę cię przekonywać, że można narysować wiele różnych modeli, które w lepszym lub gorszym stopniu będą przedstawiać działanie tranzystora. Jednym z takich modeli jest model czwórnikowy. Zajmiemy się nim, i to nie tylko ze względu na program szkolny, ale przede wszystkim po to, żebyś się nie bał parametrów podawanych w katalogach i rozumiał ich sens.

Zaczynamy.

Czarna skrzynka

W mądrych książkach często używa się pojęcia czarnej skrzynki. „Czarna skrzynka” to jakiś układ spełniający określone funkcje. W środku „czarnej skrzynki” może być zamknięty na przykład chrabąszcz, układ elektroniczny albo grupa sprytnych krasnoludków. A może coś jeszcze innego… Czarna skrzynka na pewno ma wejście i wyjście. Podajemy coś na wejście, a coś pojawia się na wyjściu. Oczywiście w naszym „elektronicznym” przypadku to coś, to sygnały elektryczne podawane na wejście oraz uzyskiwane na wyjściu. Mamy więc napięcie wejściowe – oznaczamy je Uwe, napięcie wyjściowe – Uwy, oraz ewentualnie prądy: wejściowy Iwe i wyjściowy Iwy. Ilustrację znajdziesz na rysunku 1.

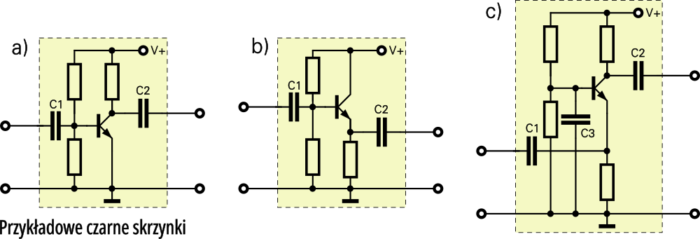
Niech we wnętrzu czarnej skrzynki cichutko siedzi tranzystor, ale nie „goły”, tylko z obwodami polaryzującymi – czyli właściwie wzmacniacz tranzystorowy. Może to wyglądać jak na rysunku 2a, 2b lub 2c.

W poprzednim odcinku tłumaczyłem sprawę różnych modeli tranzystora. Teraz podejdziemy do sprawy jeszcze inaczej. Nie będziemy wnikać w szczegóły budowy i właściwości tranzystora, tylko potraktujemy go jako czarną skrzynkę, która pełni funkcję wzmacniacza i (uważaj!) będą nas interesować jedynie napięcia i prądy wejściowe oraz wyjściowe oraz zależności nimi rządzące.

Oto prościutki przykład. Mamy czarną skrzynkę, dla której opis działania jest beznadziejnie prosty:

Uwy = 10 x Uwe

Przecież to nic innego, jak wzmacniacz (napięciowy) o wzmocnieniu równym 10. Proste jak… obręcz!

Właśnie! Wiesz już, że jeśli w czarnej skrzynce cicho siedzi wzmacniacz tranzystorowy, to musimy liczyć się z nieliniowością charakterystyki i jeśli zniekształcenia sygnału mają być małe, to przetwarzane sygnały też muszą być małe – chodzi o to, by pracować na niewielkim odcinku charakterystyki, który w przybliżeniu można uznać za prostoliniowy (porównaj rysunki 6 i 7 w poprzedniej części). Tylko w przypadku małych sygnałów możemy uważać, że (w danym punkcie pracy) tranzystorowy wzmacniacz pracuje liniowo.

Ściślej biorąc, powinniśmy zapisać:
uwy = 10 x uwe

gdzie małe literki u wskazują, iż chodzi o sygnały zmienne (domyślnie – o małej amplitudzie).

Dociekliwi czytelnicy zauważą ponadto, że tak podany wzór nie charakteryzuje wszystkich kluczowych parametrów czarnej skrzynki, a w rzeczywistości – wzmacniacza tranzystorowego. Nie wiadomo na przykład, co tam „siedzi na wejściu”, czyli jaka tam występuje oporność, a tym samym jakie prądy płyną na wejściu i na wyjściu. Wiemy, że układ wzmacnia napięcie, ale co z prądami?

Trzeba więc dodać dalsze istotne informacje. Po pierwsze podać, jakiej konfiguracji układowej (rysunek 2a, 2b czy 2c) oraz jakiego punktu pracy dotyczą parametry − zwykle wystarczy podać wartość (stałego) prądu pracy kolektora, ewentualnie napięcie stałe kolektor − emiter. Napięcia i prądy zmienne będą występować niejako na tle tego prądu i napięcia stałego. Po drugie trzeba jakoś wyrazić występujące oporności.

Czy nasz układ ma oporność wejściową (dla przebiegów zmiennych) nieskończenie wielką? Wtedy prąd wejściowy byłby równy zeru. Ale przecież oporność wejściowa nie musi być, i wcale nie jest, aż tak duża. Już teraz zapamiętaj, że generalnie oporność wejściowa tranzystora bipolarnego jest raczej mała. I to jest poważna wada, z którą można i trzeba walczyć. Jak? To już inna historia.

A wyjście? Na rysunkach 1 i 2 zaciski wyjściowe nie są podłączone. W rzeczywistości do wyjścia dołączona jest zawsze jakaś oporność obciążenia (np. opór wejściowy następnego stopnia).

Patrząc na rysunek 3 zapomnij na jakiś czas o układach z rysunku 2, o obwodach polaryzacji i o prądach stałych (problem zasilania też pomijamy – możesz sobie wyobrazić, że bateria zasilająca znajduje się wewnątrz czarnej skrzynki).

Teraz interesuje nas tylko, jak nasza czarna skrzynka zachowuje się przy podaniu na wejście małych napięć zmiennych. Jaki najprostszy model pokazywałby zachowanie naszego wzmacniacza tranzystorowego?

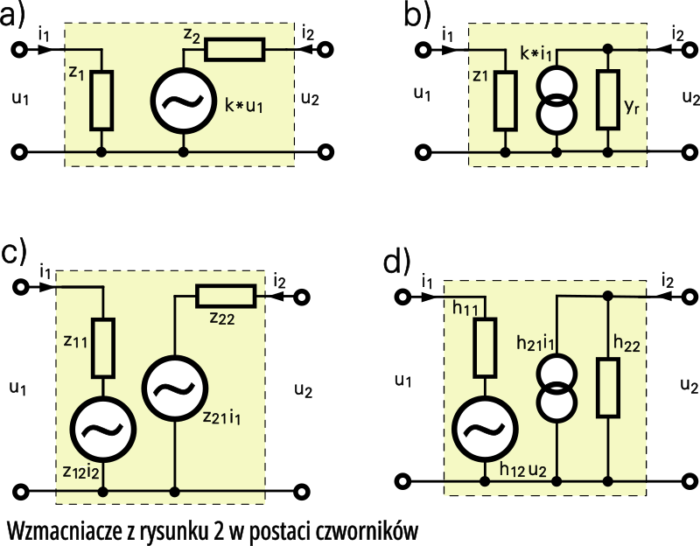
Czy na przykład czarna skrzynka, a właściwie układ tranzystorowy, ma nieograniczoną wydajność prądową? Raczej nie. Jeśli wyjście ma ograniczoną wydajność prądową, to zapewne można to potraktować jako istnienie wewnętrznej rezystancji wyjściowej. Możemy więc przedstawić naszą skrzynkę w postaci czwórnika jak na rysunku 3a lub pamiętając, że obwód kolektorowy zachowuje się jak źródło prądowe raczej jak na rysunku 3b (oporność dołączona równolegle do źródła prądowego). Zauważ, że na rysunku 3a oznaczyłem występujące oporności nie literką R czy r (rezystancja), tylko małą literką z, co pokazuje, że chodzi o oporność zespoloną – impedancję (dla przebiegów zmiennych). Nie jest to jakaś przeszkoda w rozważaniach – pomału zbliżamy się w ten sposób do zapisu, jaki znasz z książek.

A może, jeśli taki sposób opisu czarnej skrzynki miałby być w miarę precyzyjny, trzeba jeszcze uwzględnić dodatkowe czynniki, na przykład coś takiego jak wpływ napięcia wyjściowego na właściwości wejścia (wewnętrzne sprzężenie zwrotne)?

W tranzystorze rzeczywiście występuje takie wewnętrzne sprzężenie zwrotne. Na rysunku 3c reprezentowane jest przez dodatkowe źródło napięcia umieszczone w obwodzie wejściowym. I oto mamy model czwórnikowy tranzystora w pełnej krasie.

Zachowanie takiego czwórnika można i trzeba jakoś opisać równaniami. I na pewno nie wystarczy jedynie podać wartość wzmocnienia. Wzory powinny uwzględniać pokazane oporności i sprzężenie zwrotne.

Jeśli przyjmiemy, że właściwości naszego tranzystora przedstawia model czwórnikowy z rysunku 3c, to moglibyśmy napisać równania go opisujące. Mają one postać:

u₁ = z₁₁i₁ + z₁₂i₂
u₂ = z₂₁i₁ + z₂₂i₂

To są tak zwane równania impedancyjne. Nie musisz dobrze rozumieć ich sensu, zwróć tylko uwagę, że wszystko tu zgadza się z intuicją. Mianowicie z₁₁ to niewątpliwie oporność (ściślej impedancja) wejściowa, z₂₂ to oczywiście oporność (impedancja) wyjściowa. Parametr z₂₁ niewątpliwie reprezentuje wzmocnienie, natomiast z₁₂ reprezentuje wspomniane wewnętrzne sprzężenie zwrotne. Przemyśl to dobrze! Wprowadzone właśnie parametry z świetnie zgadzają się z intuicją!

Nieco gorzej jest ze spotykanymi częściej tak zwanymi parametrami hybrydowymi tranzystora oznaczonymi: h₂₁, h_21e, h_21E, h_11b, h_12e, h₂₂. Nie bój się ich! Nadmienię tylko, że literka h pochodzi od słowa hybryd (mieszany). Za chwilę się okaże, że owe: h₁₁, h₁₂, h₂₁ i h₂₂ niosą dokładnie taką samą treść jak oswojone właśnie parametry z. Parametry h powiążemy z siecią (modelem) pokazaną na rysunku 3d. A oto stosowne równania:

u₁ = h₁₁i₁ + h₁₂u₂
i₂ = h₂₁i₁ + h₂₂u₂

Może wyda ci się to dziwne, nieprzyjazne i zbyt skomplikowane. Jeśli uważasz, że to są skomplikowane zależności, to się grubo mylisz. Potrzebne wzory akurat nie są specjalnie skomplikowane i wcale nie trzeba znać rachunku macierzowego, by z nich skorzystać.

Porównaj te dwa równania z poprzednimi. Czy już widzisz, że h₁₁ to właściwie z₁₁ czyli impedancja wejściowa? Świetnie! Parametr h₂₁, podobnie jak z₂₁, reprezentuje wzmocnienie – tym razem prądowe. Podobnie jak z₂₂, również h₂₂ ma ścisły związek z opornością wyjściową, czy też wydajnością prądową. Zauważ, że prąd wyjściowy i₂ to prąd wejściowy i₁ pomnożony przez współczynnik wzmocnienia prądowego h₂₁, ale zmieniony o wartość h₂₂u₂ (podpowiem, że prąd ten jest pomniejszony, bo h₂₂ może mieć i ma wartość ujemną).

Analogicznie jak z₁₂, także h₁₂ reprezentuje wpływ napięcia wyjściowego na wejście. Nic więc dziwnego, że parametry te mają następujące nazwy:

h₁₁ – rezystancja (ściślej impedancja) wejściowa przy zwarciu wyjścia,
h₁₂ – współczynnik sprzężenia zwrotnego przy rozwartym wejściu,
h₂₁ – współczynnik wzmocnienia prądowego przy zwartym wyjściu,
h₂₂ – konduktancja (odwrotność rezystancji, a ściślej admitancja) wyjściowa przy rozwartym wejściu.
W zagranicznych katalogach spotyka się odmienne oznaczenia parametrów h.
h₁₁ – hie input impedance (i input – wejście),
h₁₂ – hre reverse voltage ratio (r – reverse – wsteczny),
h₂₁ – hfe small signal current gain (f – forward – w przód),
h₂₂ – hoe output admitance (o – output – wyjście).

Czy jednak nie jest to dla ciebie strasznie obce i niezrozumiałe sformułowanie „przy zwartym wyjściu, rozwartym wejściu”? Jak na przykład można zmierzyć parametry tranzystora „przy zwarciu wyjścia”? Przecież zwarcie wyjścia uniemożliwi pracę tranzystora!

Bez sensu?
Hop, hop, nie tak prędko!

Pamiętaj, że rozważamy parametry dla prądu zmiennego. A więc jeśli nasz tranzystor będzie pracował w układzie z rysunku 2a, to wspomniane zwarcie zacisków wyjściowych dla przebiegów zmiennych zapewni kondensator C2 o odpowiednio dużej pojemności. Oporność (reaktancja) kondensatora o wielkiej pojemności będzie na tyle mała, że możemy ją potraktować jako zwarcie. Kondensator ten jednocześnie odetnie składową stałą, umożliwiając przepływ prądów stałych, właściwą polaryzację i pracę tranzystora. Przykładowe układy pomiarowe parametrów h znajdziesz na rysunku 4 oraz na rysunku 5 w poprzedniej części. Proste?

Okazało się więc, że nie jest to takie straszne do zrozumienia.

Ale jeśli jeszcze mózg ci trochę pracuje zapytasz: a do czego mi są potrzebne te całe parametry h?

Służę odpowiedzią. Teoretycznie ma to wyglądać tak: przypuśćmy, że musisz zaprojektować wzmacniacz tranzystorowy. Trzeba, żeby ten wzmacniacz miał określone wzmocnienie A, oporność wejściową Rwe i oporność wyjściową Rwy. W katalogu tranzystorów znajdujesz wartości parametrów h, wybierasz układ pracy tranzystora (wg rysunku 2: ze wspólnym emiterem, wspólnym kolektorem, albo wspólną bazą), podstawiasz do nieskomplikowanych wzorów, przeliczasz, dobierasz napięcie zasilania. Na koniec wyliczasz wszystkie rezystancje ustalające stałoprądowy punkt pracy i oto obliczyłeś wszystkie elementy potrzebnego ci wzmacniacza. Zaprojektowałeś wzmacniacz.

Tak to wygląda w teorii i takimi zadaniami katują w szkole i na studiach. Natomiast w praktyce, owszem, przeprowadzamy pewne obliczenia, ale niewiele ma to związku z omawianymi właśnie parametrami h i modelem tranzystora z rysunku 3d.

Parametry h

Teraz już nie boisz się parametrów h. Z parametrem h₁₁ nie masz problemu – jest to po prostu oporność (ściślej – impedancja) wejściowa. Nic nowego – omawialiśmy to już w poprzednim odcinku (porównaj rysunek 8).

Sprawa wpływu wyjścia na wejście reprezentowana jest przez parametr h₁₂. Parametr ten należy uwzględnić w dokładniejszych obliczeniach, ale ponieważ sprzężenie to jest niewielkie, przy obliczeniach większości układów amatorskich można go po prostu pominąć (czyli wrócić do uproszczonego modelu z rysunku 3a i 3b).

Analogicznie, przy obliczaniu większości prostych układów tranzystorowych można pominąć parametr h₂₂. Nie można go pominąć tylko w tych nielicznych układach pracy, gdy w kolektorze umieszczone jest obciążenie o wyjątkowo dużej oporności. O tym za chwilę.

Nie powinien sprawić ci kłopotu parametr h₂₁ – „współczynnik wzmocnienia prądowego przy zwartym wyjściu”. Współczynnik wzmocnienia prądowego natychmiast skojarzy ci się z parametrem β, który określiliśmy jako stosunek prądu kolektora do prądu bazy. I rzeczywiście jesteś niedaleko prawdy.

Ale to nie koniec

Zwróć uwagę, że najczęściej na końcu oznaczenia h₂₁ umieszczona jest jeszcze literka. Może to być mała literka e, c lub b. Jak się może domyślasz, parametry te dotyczą tranzystorowych wzmacniaczy małych napięć zmiennych, pracujących w konkretnej konfiguracji: wspólnego emitera, kolektora albo bazy. Czyli podstawowych układów z rysunków: 2a (wspólny emiter – OE), 2b (wspólny kolektor – OC) i 2c (wspólna baza – OB).

Ale to nadal nie koniec − w katalogach i książkach spotkasz też obok oznaczenia h_21e także oznaczenie h_21E. Duża litera E wskazuje nie tylko, że parametr dotyczy układu ze wspólnym emiterem, ale przede wszystkim informuje, że jest to wzmocnienie dla prądu stałego (w literaturze często zamiast h_21E spotkasz h_FE określane też jako DC current gain, czyli wzmocnienie dla prądu stałego).

Czy h_21e = h_21c = h_21b i czy na przykład h_11e = h_11c = h_11b?

Czy β i h_21e to to samo? A może β to raczej h_21E? A może zarówno β, h_21e i h_21E to jedno i to samo? Czy też β = h_21c? Jak myślisz?

Ściśle rzecz biorąc, nie jest to to samo. W katalogach znajdziesz tylko parametry h dla układu wspólnego emitera − OE. Wartości niektórych parametrów h dla układów OC i OB bardzo się różnią, niemniej można je, łatwo obliczyć, korzystając ze wzorów, które znajdziesz w podręcznikach. Nie będę ci podawał tych wzorów. I ja i ty jesteśmy leniwi (prawda?), nie lubimy się nadmiernie męczyć i chcemy uprościć, co tylko się da.

I upraszczamy. Uważaj! Dla układów wspólnego kolektora i emitera rzeczywiście parametr h_21c oraz h_21e można w pierwszym przybliżeniu utożsamiać z β. Ale dla układu wspólnej bazy, h_21b ma wartość zbliżoną do jedności, wynosząc mniej więcej 0,95…0,999 (być może spotkałeś się kiedyś z parametrem zwanym [α−alfa]. Szczegółów nie będę ci tłumaczył. Jeśli do tej pory nadążałeś za mną, doskonale poradzisz sobie ze zrozumieniem właściwości wzmacniaczy w konfiguracji: OE, OC i OB, których obszerne (i nudne jak na mój gust) opisy znajdziesz w podręcznikach.

Zapamiętaj tylko, że choć parametry h₁₂, h₂₂ (a wbrew pozorom także h₁₁) odgrywają mniejszą rolę i w amatorskiej praktyce często się je pomija, o tyle katalogowego parametru h₂₁ lekceważyć nie można, bo głównie on decyduje o właściwościach wzmacniaczy tranzystorowych. Za chwilę zajmiemy się tym bliżej, a teraz parę uwag dla bardziej zaawansowanych.

Znaczenie h22 (dla zaawansowanych)

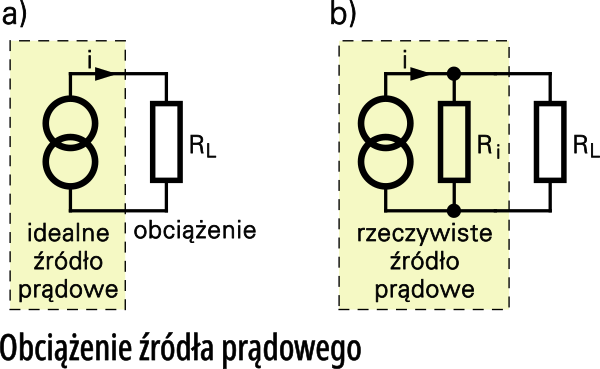
W niektórych zastosowaniach nie wolno pomijać znaczenia parametru h₂₂. Problem ilustruje rysunek 5.

W jednym z wcześniejszych odcinków tłumaczyłem ci, co to jest źródło prądowe. Dowiedziałeś się, że o wielkości sygnału napięciowego na takim źródle (na kolektorze tranzystora) decyduje głównie wartość oporności obciążenia – czym większa oporność obciążenia, tym większy sygnał wyjściowy. Zakładając, że obwód kolektorowy to idealne źródło prądowe (rys. 5a), można prosto obliczyć zmiany napięcia wyjściowego, jeśli zmiany prądu kolektora będą wynosić, powiedzmy ΔI =1 mA to:

ΔU = ΔI × R_L

Czym większa oporność obciążenia R_L, tym większy sygnał wyjściowy. Czy to jednak znaczy, że zwiększając oporność obciążenia (np. przez zwiększanie wartości rezystora w obwodzie kolektorowym lub zastosowanie obciążenia w postaci zewnętrznego źródła prądowego) można dowolnie zwiększać napięcie wyjściowe, a tym samym dowolnie zwiększać wzmocnienie wzmacniacza tranzystorowego? Niestety nie i to z kilku powodów.

Przede wszystkim obwód kolektora nie jest idealnym źródłem prądowym – sygnalizuje to rysunek 3b i 3d, gdzie niejako wewnątrz tranzystora, równolegle ze źródłem prądowym, włączona jest jakaś oporność. Oporność ta jest stosunkowo duża (bo jej odwrotność – przewodność (przewodność zespolona czyli admitancja h₂₂ ma małą wartość). Ale jak by nie było, oporność ta jest jakimś wstępnym obciążeniem dla źródła prądowego. Dołączenie zewnętrznego obciążenia może tylko zmniejszyć całkowitą rezystancję obciążenia – porównaj rysunek 5b. Na pewno wypadkowa rezystancja obciążenia nie będzie nigdy większa niż wewnętrzna rezystancja R_I.

Jeśli tak, to nawet stosując bardzo dużą oporność w kolektorze tranzystora, nie zwiększysz całkowitej oporności powyżej:

R_max = 1/h₂₂

Tym samym nie możesz uzyskać dowolnie dużego napięcia na wyjściu.

Generalny wnioski są następujące:

− nie można traktować obwodu kolektorowego tranzystora jako idealnego źródła prądowego,

− o wartości maksymalnego wzmocnienia napięciowego wzmacniacza tranzystorowego zdecyduje nie wartość wzmocnienia prądowego h₂₁, tylko h₂₂.

Nadążasz? Na rysunku 5b zaznaczyłem oporność (rezystancję) R_I dołączoną równolegle do źródła prądowego. Natomiast na rysunku 3b i 3d zaznaczone są nie tyle oporności, tylko przewodności (zespolone czyli admitancje – stąd literka y na rys 3b). Na tym poziomie rozważań nie ma to znaczenia, możesz traktować je wszystkie jako rezystancje. Zresztą te informacje nie są niezbędne początkującym (którzy być może nadal nie bardzo rozumieją o co chodzi). Ale powinni o tym pamiętać wszyscy bardziej zaawansowani, którzy będą stosować tranzystory w roli źródeł prądowych, albo chcieliby umieścić w obwodzie kolektora nie rezystory, tylko źródła prądowe.

Mam pytanie: czy w twoich wzmacniaczach tranzystorowych oporność wyjściowa całego wzmacniacza rzeczywiście wyznaczona jest przez h₂₂? Jeśli myślisz, że tak, to się grubo mylisz. Pamiętaj, że analizujemy działanie tranzystorów w teoretycznych układach pracy. Właśnie tak możemy śmiało nazwać „książkowe”, podstawowe układy pracy: OE, OC, OB z rysunku 2, a układy pomiarowe wyglądają podobnie jak na rysunku 4 oraz rysunku 5 w poprzedniej części. Ty w praktyce będziesz stosował wzmacniacze, gdzie w obwodzie kolektora umieszczony jest rezystor. Jaka będzie wtedy rezystancja wyjściowa (dla przebiegów zmiennych)?

Wrócimy do tej kwestii w jednym z następnych odcinków, a już teraz zapamiętaj, że oporność wyjściowa praktycznie jest równa rezystancji rezystora umieszczonego w obwodzie kolektora (bowiem oporność związana z parametrem h₂₂ ma bardzo dużą wartość i niewiele się zmienia). A teraz wracamy do parametru h₂₁.

h₂₁

To jak jest z używanym do tej pory, nieprecyzyjnym parametrem oznaczanym β? Czy do praktycznych obliczeń potrzebne są dokładne wartości h_21e i h_21E z katalogu?

Zajmijmy się tym bliżej. Poniższa tabela zawiera katalogowe dane tranzystorów BC107…109.

hFE − DC Current Gain IC =2 mA VCE =5 V
typ tranzystora	minimalne wartości	typowe wartości	maksymalne wartości
BC107	110	230	450
BC107 Gr. A	110	180	220
BC107 Gr. B	200	290	450
BC108	110	350	800
BC108 Gr. A	110	180	220
BC108 Gr. B	200	290	450
BC108 Gr. C	420	520	800
BC109	200	350	800
BC109 Gr. B	200	290	450
BC109 Gr. C	420	520	800
hfe Small Signal Current Gain IC =2 mA f = 1 kHz VCE =5 V
typ tranzystora		typowe wartości
BC107		250
BC107 Gr. A		190
BC107 Gr. B		300
BC108		370
BC108 Gr. A		190
BC108 Gr. B		300
BC108 Gr. C		500
BC109		370
BC109 Gr. B		300
BC109 Gr. C		550

Z porównania danych z tabeli wynikają dwa główne wnioski. Po pierwsze, dla tranzystorów tego samego typu, nawet z tej samej grupy trzeba liczyć się ze znacznym rozrzutem wartości wzmocnienia prądowego pomiędzy poszczególnymi egzemplarzami. Po drugie, wzmocnienie dla prądu stałego (DC Current Gain czyli h_21E) nie jest dokładnie równe wzmocnieniu dla małych przebiegów zmiennych (h_21e).

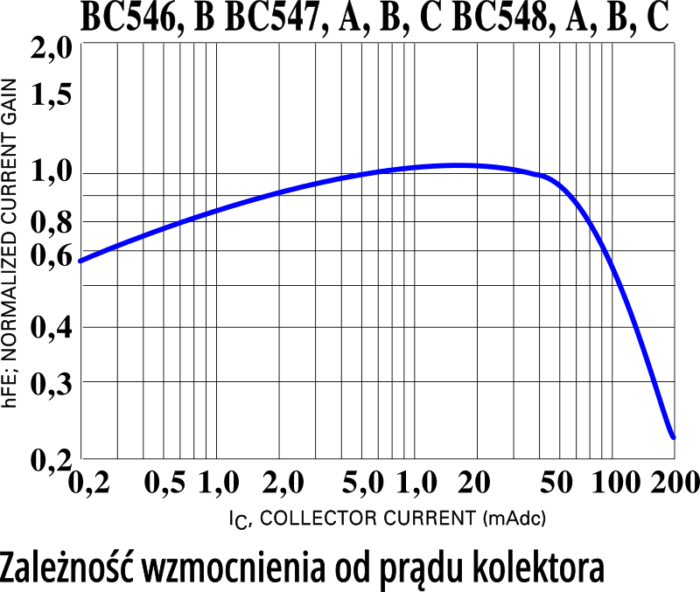
Idźmy jeszcze krok dalej. Rysunek 6 pokazuje zależność wzmocnienia stałoprądowego (czyli h_21E) od prądu kolektora dla tranzystorów BC546…BC548.

Ze względu na rozrzut między egzemplarzami, oś pionowa wyskalowana jest w procentach, a nie w wartościach wzmocnienia. Wyraźnie widać, że wzmocnienie maleje przy bardzo małych oraz stosunkowo dużych prądach kolektora. Pokrewne dane dotyczące tranzystorów BC546…548 zawarte są w poniższej tabeli.

Wzmocnienie stałoprądowe tranzystorów BC546…548 (UCE=5 V)
typ tranzystora	prąd kolektora	minimalne wartości	typowe wartości	maksymalne wartości
547A/548A	10 mA		90
546B/547B/548B	10 mA		150
548C	10 mA		270
546	2 mA	100		450
547/548	2 mA	110		800
547A/548A	2 mA	110	180	220
546B/547B/548B	2 mA	200	290	450
547B/548C	2 mA	420	520	800
547A/548A	100 mA		120
546B/547B/548B	100 mA		180
548C	100 mA		300

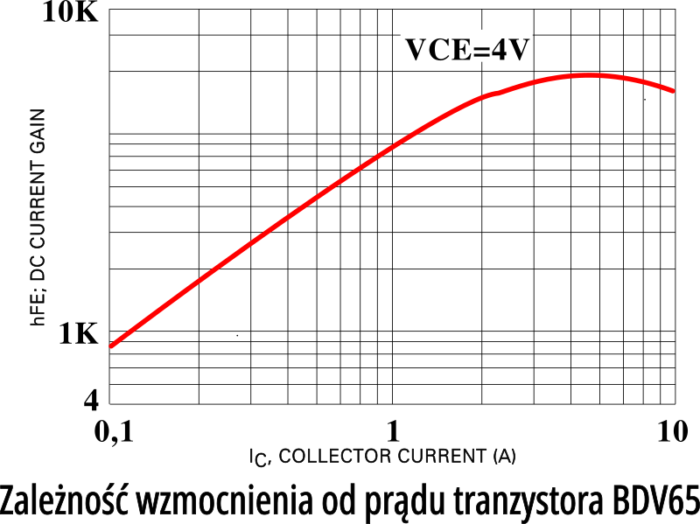
Jeszcze inaczej jest w przypadku tranzystora mocy (w układzie Darlingtona) typu BDV65 – pokazuje to rysunek 7 (Jeśli nie wiesz jeszcze, co to jest ten „Darlington“, nie przejmuj się. Czytaj dalej i wyciągaj wnioski. A do „Darlingtona“ jeszcze wrócimy).

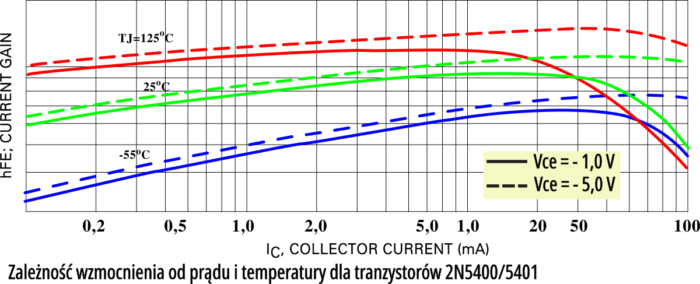
Mało tego! Rysunek 8 pokazuje podobną zależność wzmocnienia w funkcji prądu kolektora, ale dla trzech różnych temperatur i dla dwóch napięć kolektora. Wykres dotyczy dość popularnego tranzystora 2N5400/5401.

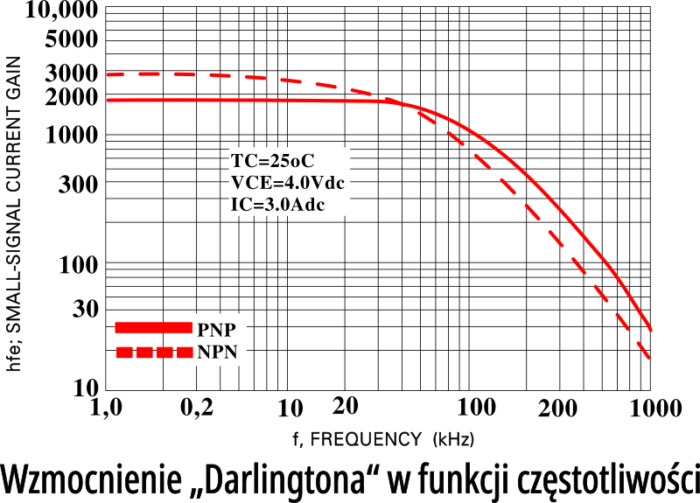
A i to nie koniec! Rysunek 9 przedstawia zależność wzmocnienia od częstotliwości tranzystorów mocy (Darlingtona) typu 2N6040…6045. Jak widać, wzmocnienie szybko spada ze wzrostem częstotliwości. Na szczęście tak małe pasmo mają tylko (i to nie wszystkie) tranzystory Darlingtona. Pojedyncze tranzystory małej i dużej mocy mają pasmo znacznie szersze.

Przeanalizuj przedstawione informacje. I co? Czy katalog pozwoli określić wzmocnienie danego tranzystora? Wszystko wskazuje, że nie! Może trzeba je po prostu zmierzyć?

Nie myśl jednak, że rozwiążesz problem mając multimetr cyfrowy z funkcją pomiaru wzmocnienia tranzystorów. Co zmierzysz? Zmierzysz wzmocnienie stałoprądowe przy nieznanym prądzie kolektora. A w twoim układzie tranzystor będzie pracował przy innym prądzie kolektora… I wzmocnienie stałoprądowe (nie mówiąc o zmiennoprądowym) będzie inne. A temperatura, częstotliwość?

Popadasz pomału w rozpacz? Czyżby miało się okazać, że cała wiedza o parametrach hybrydowych zda się psu na budę, bo „często pomijamy h₁₁, h₁₂, h₂₂”, a z kolei wartość h₂₁ jest niewiadoma ze względu na koszmarnie duży rozrzut parametrów pomiędzy egzemplarzami oraz ze względu na zależność od prądu kolektora, temperatury i częstotliwości pracy?

Aż tak źle nie jest!

Na pewno możesz zmierzyć parametry konkretnego egzemplarza w warunkach, w jakich będzie pracował. Ale w praktyce coś takiego robimy bardzo rzadko.

No to jaką wartość wzmocnienia prądowego masz wziąć do ewentualnych obliczeń?

Uważaj! Doszliśmy do bardzo ważnych wniosków praktycznych:

Po pierwsze do poważnych obliczeń projektowych trzeba wziąć spodziewane parametry najgorszego egzemplarza. A do obliczeń mniej poważnych? Niestety, tak samo! Nawet gdy zmierzysz wzmocnienie konkretnego egzemplarza dla przewidywanych warunków pracy. Bo co wtedy, gdy tranzystor się zepsuje i ktoś go wymieni na jakikolwiek egzemplarz tego samego typu?

W katalogu szukaj więc tylko wskazówek: jakie może być wzmocnienie minimalne związane z rozrzutem, prądem kolektora czy częstotliwością.

Po drugie, tranzystory trzeba wykorzystywać w taki sposób, żeby nieuniknione rozrzuty ich parametrów nie wpływały na działanie układu. Jak? Stosując układy pracy nieco inne, niż te podstawowe, „książkowe”, pokazane na rysunku 2. Sprawę tę omówimy w jednym z następnych odcinków. A już teraz ci powiem, że zawsze warto stosować tranzystory o jak największej wartości wzmocnienia prądowego. I to wszystko!

Podsumowanie

Jeśli tak, to po co ta cała zabawa z czarnymi skrzynkami, modelami, itd.? Komu potrzebne były teoretyczne rozważania?

Nie denerwuj się! Tłumaczę ci tu łopatologicznie bardzo ważną, i w sumie dość prostą sprawę: chcesz przecież zostać konstruktorem i projektować układy, a przynajmniej zrozumieć działanie tranzystora. Okazało się, że ten nasz tranzystor to paskudny twór, i wcale nie tak łatwo opisać precyzyjnie jego parametry, by potem przeprowadzić dokładne obliczenia projektowe. Żeby dokładnie opisać jego działanie należałoby posługiwać się dość złożonym modelem, co najmniej takim jak na rysunku 3 z poprzedniego odcinka lub jeszcze bardziej skomplikowanym.

Uważasz, że dwa odcinki poświęcone modelom tranzystora to dużo? Jeśli tak, to zajrzyj do podręczników ze szkoły średniej, albo lepiej akademickich, a przekonasz się, ile tam poświęcono miejsca temu tematowi, a także jak katuje się uczniów i studentów, każąc im przeprowadzać obliczenia opierające się na arbitralnie przyjętych (żeby nie powiedzieć − wyssanych z palca) wartościach parametrów h.

Nie miej pretensji do mnie, bo to nie z mojej winy okazało się, że przeciętny konstruktor−amator (i nie tyko amator) nie przeprowadza obliczeń z wykorzystaniem parametrów h. Przedstawiony materiał ma ci jedynie rozszerzyć horyzonty i pomóc wyciągnąć pewne wnioski.

Teraz nie będziesz się bał katalogowych parametrów h. Z grubsza wiesz, jaki sens ma każdy z nich. Okazało się to wszystko łatwe do zrozumienia. Jeśli więc będziesz chciał przeprowadzać teoretyczne obliczenia, skorzystasz z katalogowych parametrów h, związanych z rysunkiem 3b i odpowiednich wzorów (których ci tu nie podałem, a które straszą w licznych podręcznikach). Ale mnie w to nie mieszaj! Ja w następnych odcinkach zajmę się praktycznymi sposobami obliczeń prostych wzmacniaczy tranzystorowych, a do tego będzie potrzebna tylko szacunkowa wartość wzmocnienia prądowego.

Piotr Górecki