Wokół Arduino. Napisy i inne zakrętasy, część 1

Zajmiemy się napisami – łańcuchami tekstowymi. Z jednej strony wiemy, że w komputerze wszystkie dane to zera i jedynki. A przy komunikacji komputer–człowiek (mikroprocesor–człowiek) na ekranie trzeba wyświetlić napisy i liczby w sposób zrozumiały dla człowieka.

Na pewno nie w postaci ciągów zer i jedynek. Z kolei w drugim kierunku trzeba wprowadzić do komputera/procesora teksty i liczby – zapewne właśnie w postaci zer i jedynek, bo jakże mogłoby być inaczej. To bardzo obszerne zagadnienie można podzielić na dwie, a raczej trzy odrębne części.

Jedna sprawa to teksty, mówiąc w uproszczeniu: napisy składające się z liter (ale też innych znaków). Druga sprawa to liczby. I tu mamy dwie dodatkowe odrębne kwestie. Jedna to sprawa liczb „mniejszych, większych, ułamkowych” oraz sposób ich reprezentacji w komputerze za pomocą zer i jedynek. W grę wchodzą tu typy zmiennych (m.in. byte, char, int, long, float, double) i tym bardzo ważnym zagadnieniem zajmiemy się w oddzielnych artykułach. A teraz przyjmujemy tylko, że w komputerze/procesorze mamy rozmaite liczby, a wszystkie w sumie są mniejszymi i większymi zbiorami zer i jedynek. W tym artykule zajmiemy się drugim aspektem związanym z liczbami. Otóż teraz nie interesują nas szczegóły, jak liczby są reprezentowane/kodowane w procesorze i jego pamięci, tylko interesuje nas dwustronna komunikacja, przesyłanie, przekazywanie na drodze procesor–człowiek (człowiek–procesor) zarówno wartości liczbowych, jak też napisów – tekstów.

Procesor najczęściej przekazuje nam teksty i dane liczbowe, prezentując je na jakimś wyświetlaczu/ekranie. Z kolei my wprowadzamy do komputera napisy i liczby najczęściej za pomocą jakiejś klawiatury. Po pierwsze robimy to, pisząc program, po drugie czasem także przekazujemy jakieś liczby do procesora podczas pracy programu. Interesuje nas też, jak reprezentowane i przesyłane są napisy i liczby między komputerami/procesorami. Aby to zgłębić, musimy wrócić do podstaw. Zacznijmy od tekstów – napisów, a potem zajmiemy się problemem liczb i cyfr.

Liczby dwójkowe i tekst…

W komputerze wszelkie dane to zera i jedynki. Elementarną porcją danych jest bajt, czyli paczka ośmiu bitów. W jednym bajcie można zapisać 256 różnych kombinacji zer i jedynek: od 00000000 do 11111111. Niewiele myśląc, zwykle mówimy, że są to ośmiobitowe liczby dwójkowe  o wartości 0…255 (dziesiętnie).

Owszem, dla wygody można potraktować kombinację ośmiu zer i jedynek w bajcie jako liczbę całkowitą w zakresie 0…255. Można, ale dana kombinacja zer i jedynek oraz odpowiadająca jej liczba (0…255) mogą też znaczyć coś innego. Na przykład mogą oznaczać (kodować) litery. Trzeba tylko wymyślić – stworzyć i potem praktycznie wykorzystać kod: kombinacji zer i jedynek oraz związanej z tym liczbie ma odpowiadać litera, która będzie wyświetlana na ekranie. Taki kod jednoznacznie powiąże liczby w komputerze ze znakami graficznymi, wyświetlanymi na ekranie. I odwrotnie: gdy na klawiaturze naciśniemy klawisz jakiejś litery, do komputera zostanie wysłana liczba dwójkowa (zestaw zer i jedynek) odpowiadająca tej literze.

Ta podstawowa idea jest prosta, a stosowny kod można wymyślić/stworzyć na mnóstwo sposobów. Na przykład liczbie 1 (kombinacji zer i jedynek 00000001) mogłaby odpowiadać pierwsza litera alfabetu, a konkretnie mała literka a, liczbie 2 (dwójkowo 00000010) – mała literka b i tak dalej. Należałoby jednak pomyśleć o przydzieleniu liczb-kodów zarówno dla liter małych (a, b, c,…), jak i dużych (A, B, C). Nie można zapomnieć o dodatkowych znakach, jak choćby przecinek, kropka, znak zapytania czy wykrzyknik. Nie można też zapomnieć o wyświetlaniu na ekranie liczb, ale o tym za chwilę.

No właśnie, chcieliśmy małej literce a przydzielić kod 1, ale może kod równy jeden należałoby przydzielić cyfrze „1”, co zapewne byłoby logicznym ułatwieniem przy korzystaniu z cyfr. Wtedy cyfrze „0” należałoby przydzielić kod równy zero.

A może kod powinien wyglądać jeszcze inaczej? Możliwości jest mnóstwo, a różne kody miałyby odmienne zalety i wady.

W każdym razie jeden bajt daje 256 kombinacji. A liter (dużych i małych) w alfabecie jest co najwyżej kilkadziesiąt. Wygląda więc na to, że do zakodowania małych i dużych liter alfabetu, dziesięciu cyfr oraz znaków interpunkcyjnych powinien wystarczyć kod zawierający znacznie mniej niż 100 znaków – symboli. Ponieważ w komputerze mamy liczby dwójkowe, możemy przypuszczać, że „kod podstawowy” mógłby być 7-bitowy, czyli zawierać do 128 symboli. Słusznie! Istnieje taki 7-bitowy „kod podstawowy”, który nazywa się ASCII.

Może się też wydawać, że kod 8-bitowy, zawierający czy raczej definiujący 256 symboli graficznych, będzie „wystarczająco duży” i pozwoli zakodować wszystkie potrzebne dodatkowe symbole, jak choćby symbol stopnia Celsjusza (°), popularny krzyżyk – hash (#), „internetową małpkę – „et” (@) i inne. Niestety, w rzeczywistości jest inaczej, o czym za chwilę.

W każdym razie tworząc kod, należałoby uwzględnić też problem sortowania liter według alfabetu: zapewne kolejne litery alfabetu powinny mieć kolejne kody – numery. Trzeba też rozwiązać problem sortowania dużych i małych liter: z jednej strony muszą one mieć oddzielne kody, ale często wielkość liter nie ma znaczenia przy sortowaniu. Problem z kodowaniem i sortowaniem dotyczy też znaków specyficznych dla danego języka. Na przykład u nas za drugą literę alfabetu należałoby uznać nie literę b (B), tylko ą (Ą). W innych językach są inne znaki charakterystyczne. Już widać, że będzie problem z napisami…

Ale na razie dokończmy sprawę „kodu ekranowego”, który zera i jedynki w komputerze jednoznacznie powiąże z symbolami graficznymi (literami, cyframi, itp.).

ASCII

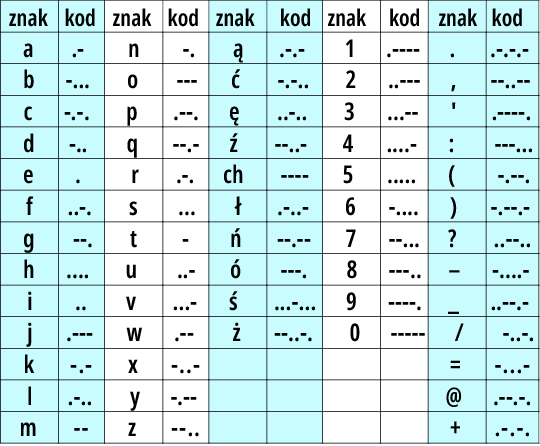
Przez dziesięciolecia takim kodem był… kod (alfabet) Morse’a – rysunek 1. Mamy tu litery (wprawdzie tylko „jedne” – małe), a do tego cyfry i najpotrzebniejsze znaki interpunkcyjne. Kropki i kreski alfabetu Morse’a mogą kojarzyć się z zerami i jedynkami, ale kod ten nie był wykorzystywany w komputerach.

W latach 60. przyjęto w USA standardowy kod, który miały i musiały wykorzystywać wszystkie ówczesne komputery. Nazywany jest „standardowym amerykańskim kodem do wymiany informacji” (American Standard Code for Information Interchange), w skrócie ASCII (czytaj: aski). W komputerach wykorzystano kod, który już wcześniej stworzono na potrzeby telekomunikacji, gdzie był stosowany w elektromechanicznych dalekopisach. Fotografia 2 z Wikipedii pokazuje dalekopis (telex) Siemens T100, który jak widać, jest odmianą elektrycznej maszyny do pisania.

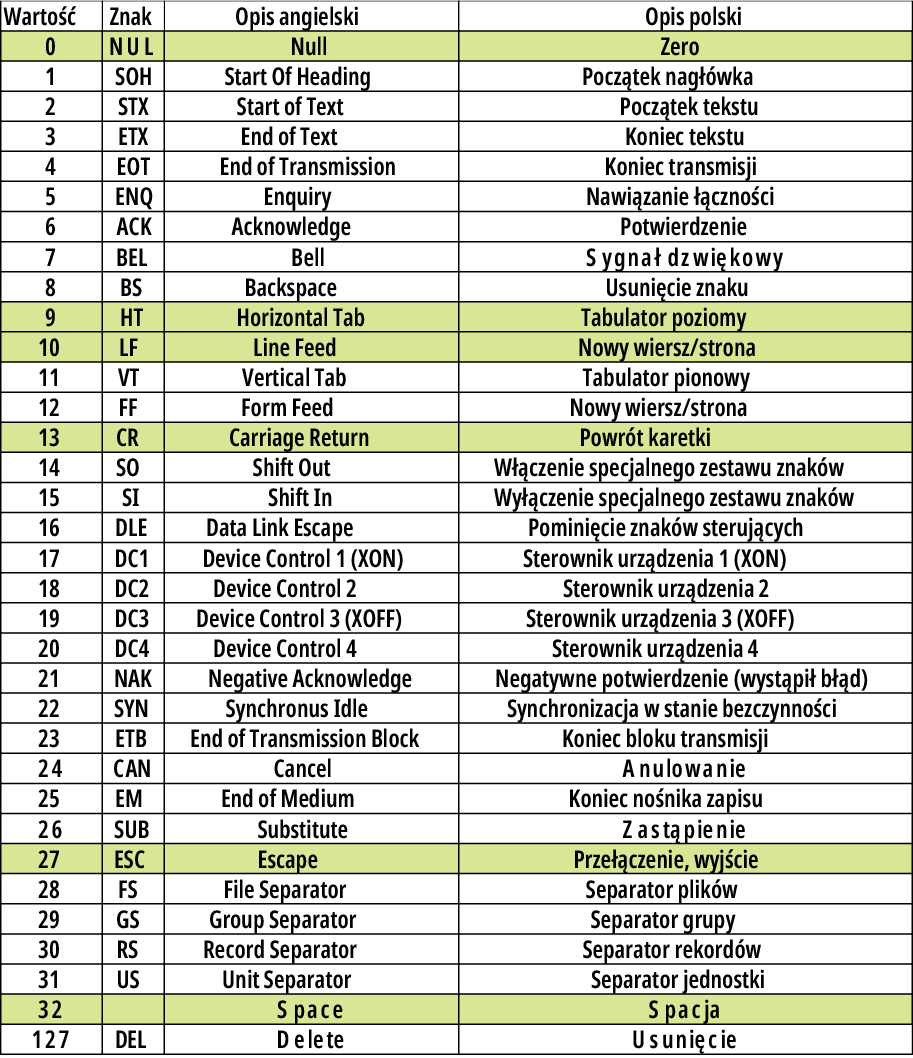
Rysunek 3 pokazuje wszystkie drukowalne znaki – symbole dostępne w kodzie ASCII. Oprócz nich w kodzie ASCII są też liczne kody „niedrukowalne”, w tym sterujące, pokazane na rysunku 4.

W tym 7-bitowym kodzie pierwsze 32 wartości (o numerach 0…31) i ostatni 127, to kody sterujące. Były bardzo ważne w elektromechanicznych dalekopisach, a w komputerach wykorzystywane są tylko niektóre z nich, przede wszystkim:

kod nr 13 CR (Carriage Return)

kod nr 10 LF (Line Feed)

kod nr 27 ESC (Escape) oraz

kod nr 9 TAB (Horizontal Tab), czyli znak tabulacji (tabulator) pomocny przy tworzeniu tabel i kolumn. Kod o numerze 32 jest w zasadzie drukowalny, ale niewidoczny – to spacja, czyli przerwa między literami. Kod 0 to kod „pusty”: nie reprezentuje ani kodu sterującego, ani symbolu, ani cyfry zero. Wbrew pozorom, jest bardzo potrzebny, ponieważ wykorzystywany jest do wskazywania końca łańcucha tekstowego – napisu (null terminated string). Znaczenie kodu „zerowego” omówimy oddzielnie.

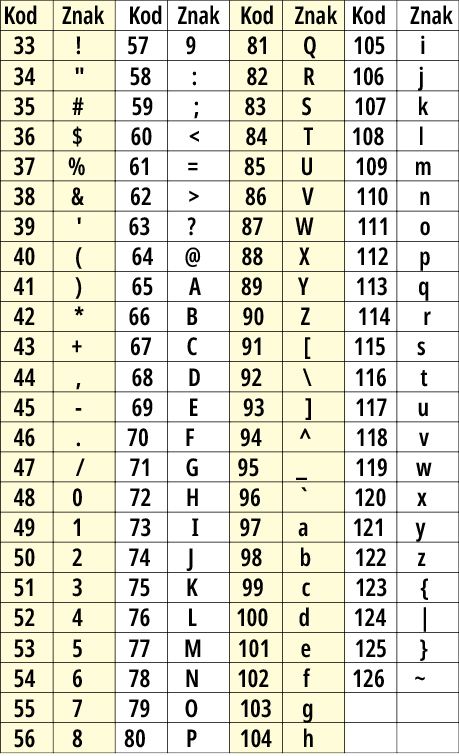
Jak pokazuje rysunek 5, kody drukowalne o niższych numerach, zaczynających się od 33, reprezentują znaki interpunkcyjne i specjalne. Cyfry 0…9 mają kody ASCII od 48 do 57, co w pierwszej chwili wydaje się bardzo dziwne. Duże litery A…Z mają kody od 65 do 90, a małe litery od 97 do 122. W „przerwach” (58…64, 91…96, 123…126) mamy jeszcze inne znaki graficzne.

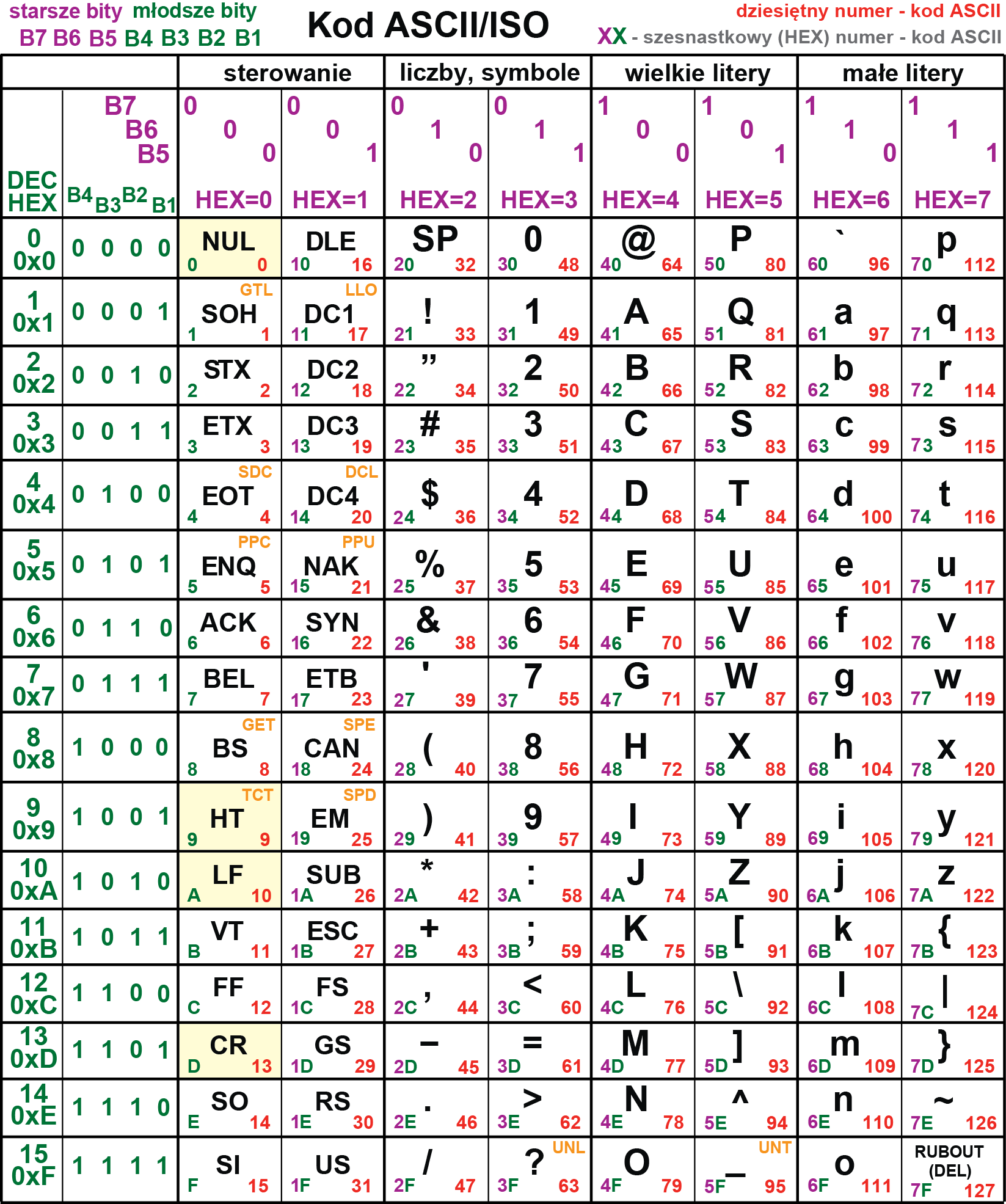
Spotykany w wielu źródłach sposób prezentacji jak na rysunkach 4 i 5 jest jak najbardziej prawidłowy, ale nie pokazuje pewnych ważnych i pożytecznych cech kodu ASCII. Widać je dopiero na dużym rysunku 6, gdzie masz wszystkie kody ASCII – warto go wyciąć lub skserować i mieć zawsze pod ręką.

Należy zwrócić uwagę na postać dwójkową poszczególnych siedmiobitowych liczb-kodów. Zaznaczone kolorem fioletowym trzy najstarsze bity określają grupy znaków – kodów. I tak wszystkie liczby o najstarszych bitach 000 oraz 001 to kody sterujące. Gdy najstarsze bity to 010 oraz 011 – mamy kody liczb i symboli. Dopiero teraz widać, że oznaczające cyfry 0…9 kody 48 do 57 to w postaci dwójkowej 0110000 do 0111001, więc po odcięciu trzech starszych bitów (zaznaczonych kolorem fioletowym) otrzymujemy liczby 0…9 w postaci dwójkowej: 0000 do 1001.

Podobnie zwróć uwagę na kody liter: najstarszy bit kodu litery zawsze jest jedynką, a kod danej litery dużej i małej zawsze różni się tylko wartością drugiego z kolei bitu, natomiast pięć młodszych bitów dla danej litery dużej i małej ma tę samą wartość. Ma to ogromne znaczenie przy sortowaniu i wyszukiwaniu, co dokonywane jest po prostu według liczby-kodu. W języku C (C++ i Arduino), gdzie „także litera jest liczbą”, na przykład litera a o kodzie-numerze 97 jest mniejsza (!) od litery b (kod 98), bo mniejszy jest jej numer – kod ASCII.

Zapamiętaj, że „kod podstawowy” ASCII opracowany został w Ameryce na potrzeby elektromechanicznych dalekopisów, czyli specyficznych elektrycznych maszyn do pisania, a dopiero potem zaadaptowany do komputerów. Obejmuje wszystkie litery angielskiego alfabetu, szereg symboli i znaki interpunkcyjne, do czego wystarcza nie więcej niż 128 znaków-symboli.  Zwróć jednak uwagę, że 7-bitowy kod ASCII wśród 95 drukowalnych symboli nie zawiera ani „polskich liter”, ani symboli z innych alfabetów, choćby rosyjskiego, ani też dość często potrzebnych liter greckich. Aby rozwiązać problem braku znaków narodowych, przez pewien czas wykorzystywano fakt, że w komputerach mamy dane 8-bitowe, więc jeden bajt oprócz kodów ASCII pozwala określić 128 dodatkowych znaków – symboli, na przykład „polskie litery”. To prosta idea tak zwanych stron kodowych: stworzono wiele różnych stron kodowych, przy czym kody 0…127 to zawsze kody ASCII jednakowe w każdym komputerze na całym świecie, a dodatkowe kody 128…255 reprezentowały takie czy inne „znaki lokalne” potrzebne w danym kraju.

W związku z tym trzeba stworzyć kod, czyli wzajemne przyporządkowanie liczb z zakresu 128…255 i różnych zbiorów „znaków lokalnych”. Można to zrobić na wiele sposobów (o czym można się przekonać na stronie

https://pl.wikipedia.org/wiki/Kodowanie_polskich_znak%C3%B3w

w skrócie https://bit.ly/2PMotry,

gdzie podane są różne sposoby kodowania polskich znaków diakrytycznych. Większość tych kodów miała bardzo ograniczone zastosowanie. Z czasem w polskich komputerach najpopularniejsze stały się sposoby (kody, strony kodowe) oznaczane jako Windows1250 oraz ISO-8859-2.

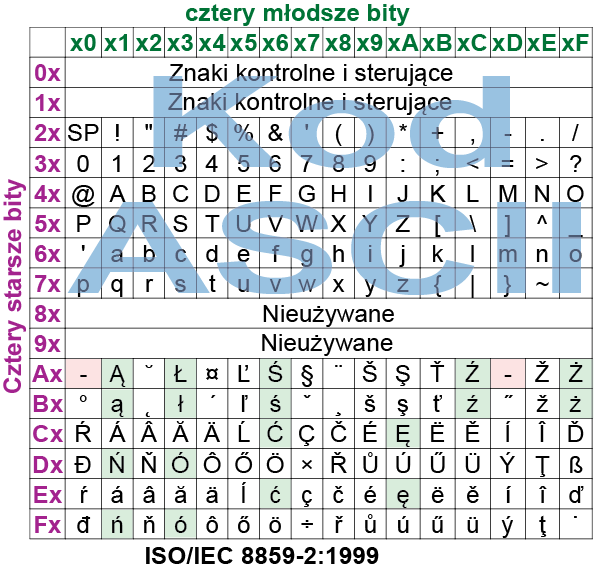
Nie będziemy ich omawiać szczegółowo, bo tracą znaczenie i dość szybko odchodzą one do historii. Rysunek 7 pokazuje tabelę ze stroną kodową ISO-8859-2, tylko narysowaną nieco inaczej niż wcześniejsza tabela z rysunku 6 (ale kolory grup bitów są zachowane). Jeszcze raz podkreślam, że kody 0…127 to  zawsze ASCII, a „znaki lokalne” mają numery-kody 128…255.

Strony kodowe z dodatkowymi znakami dla poszczególnych języków wykorzystywano zarówno w komputerach na całym świecie, jak też potem na stronach internetowych. W przypadku komputerów było to sensowne i skuteczne rozwiązanie. W przypadku Internetu i przekazywania tekstów też, ale pod warunkiem że dostępna była informacja, którą stronę kodową dla znaków 128…255 wykorzystano w danym tekście – przekazie. Często nie rozwiązywało to jednak problemu do końca i często zamiast sensownych znaków widać było na ekranie „krzaczki”. Do dziś można spotkać echa tego problemu, na przykład w napisach do filmów.

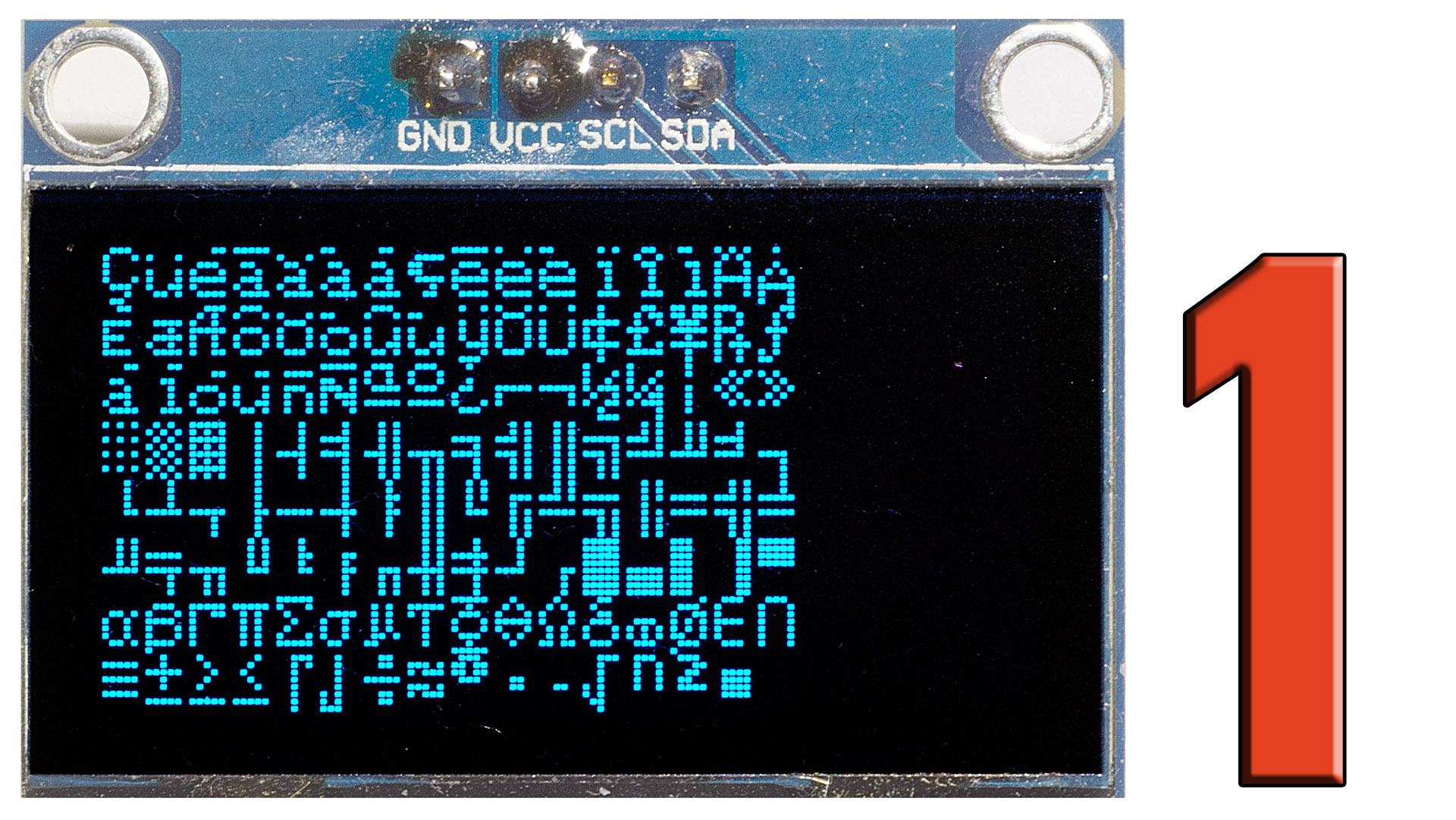
Skutecznym rozwiązaniem problemu „krzaczków” okazał się tak zwany Unikod (Unicode), stosowany coraz powszechniej. Systemowi Unicode poświęcimy oddzielny artykuł, ale jeżeli już jesteśmy przy rozszerzeniu kodu ASCII i stronach kodowych, koniecznie powinniśmy wspomnieć o popularnych wyświetlaczach znakowych, opartych na scalonych sterownikach zgodnych z HD44780 japońskiej firmy Hitachi.

Zajmiemy się tym w następnym artykule.

Piotr Górecki