Wokół Arduino. Napisy i inne zakrętasy, część 2

W pierwszej części omówiliśmy zasady kodowania tekstów – napisów i dość dokładnie zapoznaliśmy się z kodem ASCII (ISO). Zanim omówimy uniwersalny system Unicode i zaskakująco sprytne kodowanie UTF-8, musimy wspomnieć o wyświetlaczach znakowych LCD.

HD44780

Pokazany na fotografii 8 bodaj najpopularniejszy znakowy wyświetlacz LCD znakomicie ułatwia wyjaśnienie szeregu omawianych właśnie zagadnień. Wprawdzie do Arduino najczęściej podłącza się go za pomocą czterech linii danych, a ostatnio coraz powszechniej wykorzystuje się „przejściówkę” i łącze I2C, jednak generalnie wyświetlacz taki przyjmuje dane ośmiobitowe. Nie wchodząc w problem kursora, automatycznego przesuwania zawartości ekranu i innych efektów, powiemy, że wysłanie do tego rodzaju wyświetlacza liczby 8-bitowej, czyli w sumie kodu w zakresie 0…255, powoduje wyświetlenie znaku (w rzeczywistości zależnie od stanu wejścia RS bajt danych jest traktowany albo jako znak do wyświetlenia, albo jako instrukcja sterująca).

Wyświetlenie znaku polega na zaświeceniu/zgaszeniu odpowiednich punktów na matrycy 5×7. O tym, jaka będzie reakcja wyświetlacza na przysłany do niego ośmiobitowy kod, decyduje zawartość pamięci znaków ROM. Nie tylko dociekliwych zapraszam do analizy karty katalogowej układu scalonego HD44780, którą bez problemu można znaleźć w Internecie.

Oczywiście kody o numerach do 127 spowodują wyświetlenie znaków zdefiniowanych w kodzie ASCII.  My podajemy (drukowalny) kod ASCII, a sterownik wyświetlacza na podstawie posiadanej pamięci stałej ROM zaświeci i zgasi odpowiednie punkty matrycy.

W przypadku takiego wyświetlacza większość niedrukowalnych kodów ASCII nie jest wykorzystywana i producent sterownika HD44780 przewidział, że dla pierwszych ośmiu (0…7) kodów-adresów użytkownik może zdefiniować własne znaki (powtórzone pod adresami 8…15). W tym celu sterownik wyposażono w dodatkową pamięć (GC RAM), gdzie te samodzielnie zdefiniowane znaki można zapisać.

A co pokaże wyświetlacz znakowy zgodny z HD44780 dla kodów o numerach 128…255?

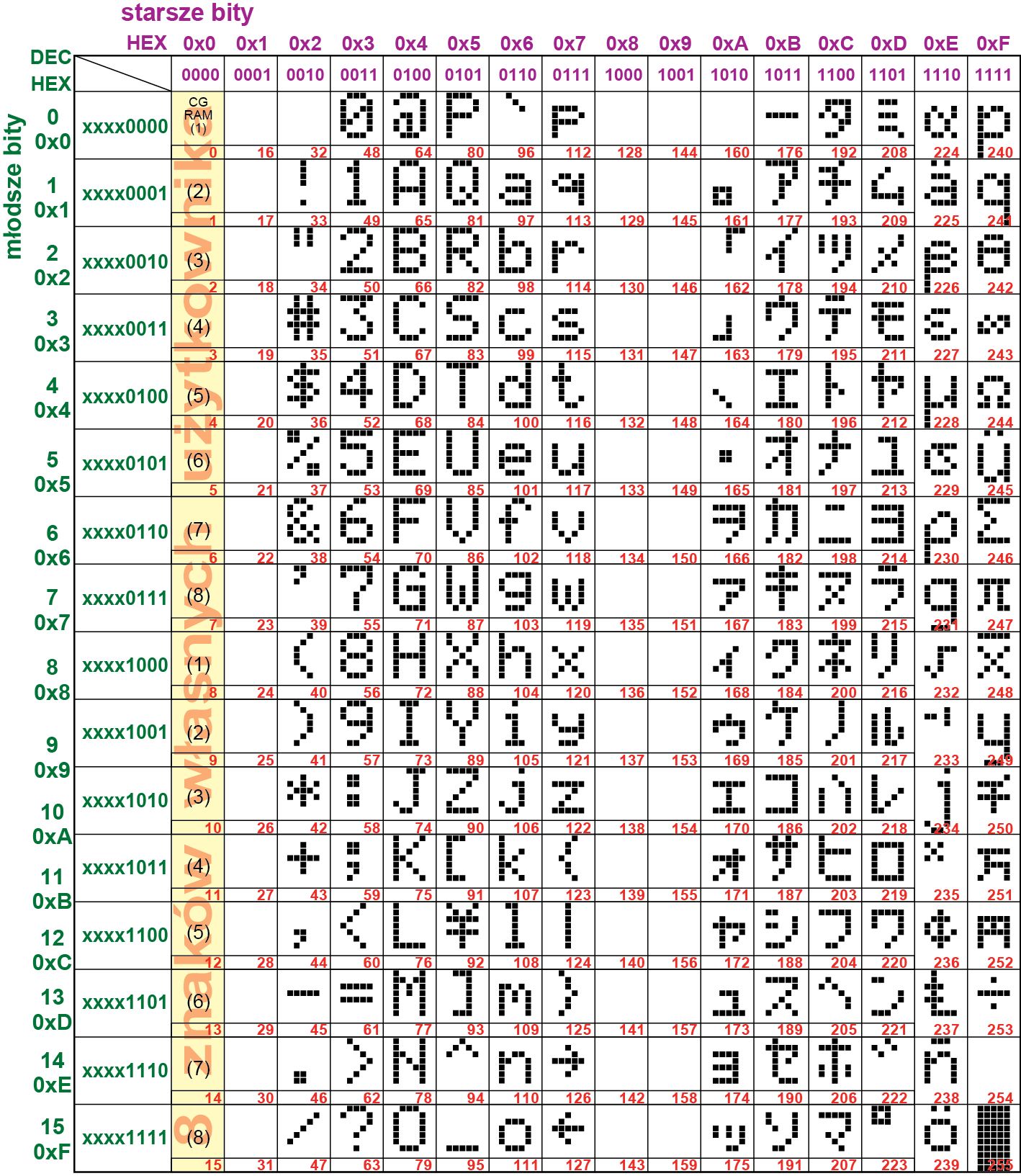
Przy dużych zamówieniach użytkownik może zamówić u producenta wersję sterownika z własną „stroną kodową” i wtedy dla wyższych kodów wyświetlacz pokaże zamówiony zestaw znaków. Jednak praktyka jest inna. Sterownik HD44780 był opracowany w Japonii i wiele wyświetlaczy po podaniu „wyższych numerów” wyświetli znaczki japońskiego alfabetu katakana oraz niektóre łacińskie i greckie litery i symbole jak pokazuje rysunek 9. Duża część wyświetlaczy trafiających na rynek polski ma taki właśnie zestaw znaków.

Często spotykana jest też „niejapońska” wersja sterownika HD44780 z inną zawartością pamięci ROM (ROM code A02), gdzie „wyższe numery” powodują wyświetlenie różnych znaków, powiedzmy „łacińskich”. Zestaw tych znaków pokazany jest na rysunku 10. Wprowadzono tu też dodatkowe znaki przy niedrukowalnych „niskich numerach” 16…31, ale niestety, nie ma tam „polskich liter” (poza ó i Ó).

Część wyświetlaczy trafiających na rynek polski ma zestaw znaków „japoński”, a inne mają zestaw „łaciński” i nie widać tego z zewnątrz. Dlatego rysunki 9 i 10 są bardzo pożyteczne, bo pozwalają po pierwsze określić, jaki wyświetlacz udało nam się kupić, a po drugie sprawdzić, czy w dostępnym w nim zestawie znaków jest potrzebny nam symbol i jaki ma numer-kod. I tak przykładowo dość często wykorzystywany symbol stopnia (°) w wersji „japońskiej” ma kod 223 (0xDF), a w wersji „łacińskiej” kod 176 (0xB0) i możemy go łatwo wyświetlić, podając stosowny numer.

Ponieważ artykuły „Wokół Arduino” mają wspierać i rozszerzać elementarny Kurs Arduino, trzeba wspomnieć, że pisząc szkic Arduino, mamy bardzo ułatwione zadanie. Z reguły w programie-szkicu wykorzystujemy bibliotekę LCD (LiquidCrystal.h) i dostępną tam, a także w innych pokrewnych bibliotekach metodę-funkcję .print(). Po prostu wpisujemy tekst, liczby i symbole, a nie numery-kody. Potem procedury biblioteczne dbają o prawidłowe ich wyświetlenie. Jednak ze znakami o kodach powyżej 127 (oraz 16…31) jest pewien kłopot, bo nasz komputer, na którym piszemy program-szkic (i edytor Arduino) wykorzystuje inny zestaw znaków dla „wyższych kodów” niż wyświetlacze LCD. Zwykle problem można obejść, właśnie sprawdzając na rysunkach 9 i 10 numer kodu danego znaku LCD, a potem wykorzystując w programie nie metodę .print(), tylko pokrewną metodę .write(), o czym za chwilę.

Zagadnienie jest szerokie, bo dotyczy nie tylko wyświetlacza LCD, ale też łącza szeregowego i biblioteki Serial, a także innych urządzeń i bibliotek. Nie będziemy zagłębiać się w szczegóły, bo nie omówiliśmy jeszcze wspomnianego unikodu. Ale wcześniej powinniśmy poruszyć kwestię liczb i cyfr.

Liczby i cyfry

Na początku artykułu przypomnieliśmy, że elementarną porcją danych jest bajt, czyli paczka ośmiu bitów i niewiele myśląc, mówimy, że bajt zawiera ośmiobitową liczbę dwójkową. Liczby te możemy zapisać – przedstawić w różny sposób.

Mianowicie można je zapisać w systemie dwójkowym (binary – BIN) właśnie w postaci 00000000…11111111, co bezpośrednio i ściśle odzwierciedla sytuację w procesorze. W komputerze 1 to tak naprawdę obecność napięcia, a 0 to brak napięcia. Ale dla ludzi taka zero-jedynkowa reprezentacja jest bardzo niewygodna. Jeśli kombinację zer i jedynek potraktujemy jako liczbę dwójkową, to można ją zapisać w systemie dziesiętnym (decimal – DEC), do którego jesteśmy najbardziej przyzwyczajeni.

Przykładowo w procesorze mamy ciąg: 11011110. Ale my powiemy, że 11011110 to liczba 222. Owszem, można tak powiedzieć i często tak mówimy.

Ale 222 to w zasadzie zestaw trzech „znaczków” – symboli, a w tym przypadku jeden znak-symbol (2), powtórzony trzykrotnie, co rozumiemy jako liczbę dwieście dwadzieścia dwa. Przyzwyczailiśmy się bowiem do systemu i zapisu dziesiętnego, który jest jednym z wielu systemów zapisu liczb.

Uznajemy, iż 222 to liczba dziesiętna trzycyfrowa. Składa się z trzykrotnie powtórzonej jednej cyfry 2. Cyfra nie jest liczbą. Cyfra to jedynie umowny znak graficzny, służący do zapisywania liczb w określonym systemie liczbowym. Natomiast liczba to pojęcie abstrakcyjne związane z porównywaniem wielkości, którego sensu uczymy się najpierw w życiu codziennym, potem w szkole.

Do zrozumiałego dla nas zobrazowania liczb (bytów abstrakcyjnych) potrzebujemy jakiegoś systemu zapisu liczb oraz znaków graficznych – w naszym przypadku cyfr, niezbyt słusznie zwanych cyframi arabskimi. Liczby można zapisywać w różny sposób. W zamierzchłych czasach, na przykład w językach hebrajskim, greckim i w łacinie u Rzymian, funkcję cyfr pełniły litery.

System dziesiętny z dziesięcioma cyframi 0…9 jest wygodny dla „zwykłych ludzi”. W komputerach (procesorach) wykorzystany jest system dwójkowy z dwiema tylko cyframi: 0, 1, gdzie cyfry te mogą też znaczyć 0: brak, fałsz, 1: jest, obecność, prawda.

Dla informatyków wygodniejszy okazuje się pokrewny system szesnastkowy (hexadecimal – HEX). Do wyświetlania liczb w postaci szesnastkowej (HEX) potrzebnych jest 16 cyfr: cyfry 0…9 mamy w systemie dziesiętnym, a umówiono się, że dla większych cyfr nie zostaną wymyślone jakieś nowe dodatkowe symbole, tylko zostaną wykorzystane znajome znaki alfabetu: A (jako cyfra szesnastkowa dziesięć), B (cyfra jedenaście),…F (cyfra piętnaście). W systemie szesnastkowym mamy więc cyfry: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, a ośmiobitową liczbę dwójkową możemy zapisać za pomocą dwóch tylko cyfr szesnastkowych w zakresie 00 do FF. Ponadto jedną cyfrę szesnastkową można łatwo „zamienić” na zbiór czterech bitów (zer i jedynek). Na przykład 11 to jedenaście w systemie dziesiętnym (DEC) oraz siedemnaście w systemie szesnastkowym (HEX) i oczywiście liczba trzy w systemie dwójkowym. W informatyce dla odróżnienia liczb szesnastkowych od dziesiętnych poprzedzamy je znakami 0x. Zapis 11 oznacza jedenaście, a zapis 0x11 to liczba szesnastkowa równa siedemnaście. B11 to liczba dwójkowa trzy.

W tym dość długim wprowadzeniu chciałem Ci pokazać, że te sam abstrakcyjny byt – liczbę, można przedstawić, zobrazować w różny sposób. W komputerze liczba zawsze reprezentowana jest jako ciąg zer i jedynek. A jeśli komputer ma nam pokazać tę liczbę, a raczej jej wartość, zazwyczaj musi dokonać jakichś operacji, by przedstawić ją nam w systemie dziesiętnym za pomocą cyfr 0…9 (i ewentualnie w ułamkach także przecinka, a częściej kropki). W każdym razie mamy dwie oddzielne kwestie: liczbę w komputerze, czyli zbiór zer i jedynek oraz taką czy inną reprezentację tej liczby za pomocą cyfr (znaków, symboli) przy wprowadzaniu liczb do programu i procesora oraz przy wyprowadzaniu ich z procesora na ekran.

Jeszcze raz przypomnijmy, że przy pisaniu programu-szkicu kluczową rolę odgrywa kompilator, który zamieni nasz szkic na program w kodzie maszynowym procesora, gdzie finalnie wszystko, także wszelkie liczby, będą mieć postać zer i jedynek. Kompilator to program na komputer PC o bardzo dużych możliwościach. Między innymi możemy w pisanym przez nas szkicu według upodobania podawać wartości liczbowe w różnej postaci: dziesiętnej (DEC), dwójkowej (BIN), szesnastkowej (HEX), a także ósemkowej (OCT). Kompilator je właściwie zrozumie, a finalnie i tak wykorzysta postać dwójkową. Najczęściej w programie piszemy liczby w postaci dziesiętnej. Ale jeżeli liczba zaczyna się od cyfry zero (podobnej do litery O), to zastanie potraktowana przez kompilator jako liczba ósemkowa. Jeżeli poprzedzimy liczbę literą B – kompilator potraktuje ją jako liczbę dwójkową (oczywiście musi zawierać jedynie cyfry 0 i 1). Jeżeli liczbę poprzedzimy zerem i literką x, kompilator potraktuje ją jako liczbę szesnastkową (może zawierać cyfry 0…9, A…F). Takie możliwości zawdzięczamy inteligencji kompilatora.

Ale Arduino oferuje też pokrewne możliwości w drugą stronę. Mianowicie w trakcie pracy programu na wyświetlaczu LCD czy na ekranie (konsoli) monitora szeregowego procesor może nam zaprezentować   liczby w postaci dziesiętnej, dwójkowej czy szesnastkowej. To już jest zasługa nie tyle kompilatora, tylko metod-funkcji zawartych w bibliotekach, a konkretnie metody .print(). Kompilator tylko wybierze i umieści w programie procesora nie wszystkie, a tylko niektóre procedury dostępne w metodzie .print(), potrzebne w danym przypadku. Ale cała inteligencja „wyprowadzania liczb na zewnątrz” zawarta jest w procedurach bibliotecznych.

Metody .print() i .write()

I właśnie wyświetlacz znakowy LCD znakomicie pomaga zrozumieć problem i rozróżnić różne aspekty omawianego zagadnienia. Przypuśćmy, że w procesorze mamy ciąg zer i jedynek 11011110. Co to jest? Czy liczba dwójkowa 222, czy kod znaku?

Jeżeli jest to liczba całkowita dwieście dwadzieścia dwa, to chcąc ją zobrazować na ekranie, nie możemy jej wysłać bezpośrednio do wyświetlacza LCD. Zgodnie z rysunkami 9, 10 wersja „japońska” wyświetliłaby nam wtedy dziwny znaczek składający się z czterech kropek, a wersja „łacińska” pokazałaby coś podobnego do połączenia liter b i p. Aby na ekranie wyświetlić liczbę 222, program w procesorze musi dokonać szeregu przeliczeń i do wyświetlacza LCD wysłać trzy razy kod cyfry dwa, czyli 50 (0x32), a konkretnie wysłać ciąg 00110010  00110010  00110010. Wtedy na wyświetlaczy zobaczymy 222. I właśnie to zadanie realizuje metoda .print(), dostępna m.in. w bibliotece LiquidCrystal.h. My pisząc szkic Arduino, nie zajmujemy się szczegółami, jak to jest realizowane.

Ktoś musiał się nieźle napracować, żeby omawiane klasy-biblioteki (poczynając od klasy zwanej Stream) i metoda .print() miały takie możliwości.

Czy to do wyświetlacza LCD, czy do portu szeregowego Serial, metoda .print() wysyła kody ASCII, by stworzyć na ekranie czytelny dla człowieka tekst, w tym liczby w różnej postaci (DEC, BIN, HEX, OCT). Wykorzystując Arduino, nie musimy rozumieć szczegółów, wystarczy znać możliwości funkcji-metody .print().

Przekazujemy do niej wartość według wzoru: .print(przekazywanaWartosc). Ale ta przekazywana wartość może mieć różną postać. W przypadku tekstów po prostu ujmujemy tekst do wyświetlenia w podwójne cudzysłowy, na przykład: Serial.print(„Dowolny Napis”);. Pojedyncze znaki wyświetlamy, ujmując je w pojedynczy cudzysłów, na przykład lcd.print(‚X’);. Jeśli liczbę całkowitą albo zawartość zmiennej chcemy wyświetlić na ekranie w postaci dziesiętnej, w programie napiszemy po prostu: lcd.print(78); albo lcd.print(zmiennaLiczbowa);. Ale jeżeli liczba ma być przedstawiona w innej postaci, określamy to, dodając do argumentu przekazywanego funkcji przecinek oraz BIN, HEX albo OCT, na przykład Serial.print(zmienna, HEX); albo lcd.print(zmienna, BIN);. To jest dość proste do zrozumienia i zapamiętania.

Ale trochę zamieszania może powstać, jeśli już w programie szkicu mamy liczby całkowite. Pisząc program, możemy je przedstawiać w dowolnej postaci, a potem procesor może nam je pokazać na ekranie w różnej postaci. Przykładowo możemy podawać wartości liczbowe dziesiętnie i zażyczyć sobie wyświetlenia ich w innej postaci:

Serial.print(78, BIN); na ekranie wyświetli: 1001110,

Serial.print(78, OCT); na ekranie wyświetli: 116,

Serial.print(78, DEC); na ekranie wyświetli: 78,

Serial.print(78, HEX); na ekranie wyświetli: 4E.

Możesz we własnym zakresie sprawdzić, co zostanie wyświetlone, jeśli analogicznie wartość liczbową podasz w postaci szesnastkowej czy dwójkowej, na przykład Serial.print(0x4E, BIN); czy Serial.print(B1001110, DEC);.

W przypadku liczb zmiennoprzecinkowych (zmiennych typu float i double) są one domyślnie wyświetlane z dokładnością dwóch miejsc po przecinku (kropce). Ale możemy określić dokładność, podając liczbę cyfr wyświetlanych po przecinku, na przykład Serial.print(zmienna_typu_float, 5);  albo Serial.print(1.23456789, 5);.

W każdym razie metoda .print() inteligentnie interpretuje, czym jest argument, który do niej przekazujemy i wyświetla go w postaci przyjaznej dla człowieka, wykorzystując i podstawoway 7-bitowy kod ASCII i jego takie czy inne rozszerzenie.

Natomiast dostępna w bibliotekach pokrewna metoda .write() jest dramatycznie prostsza. Po prostu wysyła jeden bajt, nie dokonując żadnej konwersji. Metoda .write() powoduje tylko wysłanie liczby ośmiobitowej „z procesora na zewnątrz”, a efekt zależy od tego, dokąd ta liczba trafi.

Jeśli w programie napiszemy przykładowo Serial.write(120); albo lcd.write(120);, to procesor wyśle łączem szeregowym albo do wyświetlacza LCD liczbę 120, oczywiście w postaci dwójkowej, czyli 1111000.

I co? Na ekranie konsoli monitora szeregowego i na ekranie wyświetlacza LCD zobaczymy małą literkę x, bo 120 to kod ASCII małej litery x. Ale gdy wyślemy liczbę z rozszerzonego zakresu ASCII, przykładowo Serial.write(222); albo lcd.write(222);, procesor wyśle liczbę 222 w postaci dwójkowej, czyli 11011110 i efekt na ekranie będzie zależny od tego, jak urządzenie odbiorcze potraktuje kod równy 222. Konsola na komputerze zareaguje inaczej, wyświetlacz LCD w wersji „japońskiej” inaczej, a „łacińskiej” – jeszcze inaczej.

To są bardzo ważne elementarne podstawy, ale do pełni szczęścia brakuje nam jeszcze znajomości unikodu. Trzeba też dobrze zrozumieć omawiane tu kwestie przy wprowadzaniu danych pracującego procesora. Do tych zagadnień będziemy wracać.

Piotr Górecki