Wokół Arduino. Napisy i inne zakrętasy, część 4

W poprzednim artykule (UR042) zapoznaliśmy się z unikodem i z podstawowymi zasadami kodu UTF-8. Dla uzyskania pełnego obrazu trzeba jeszcze wiedzieć, jak numer znaku w systemie unikod jest reprezentowany w UTF-8.

Zacznijmy od tego, ze na wspomnianej przed miesiącem pożytecznej stronie

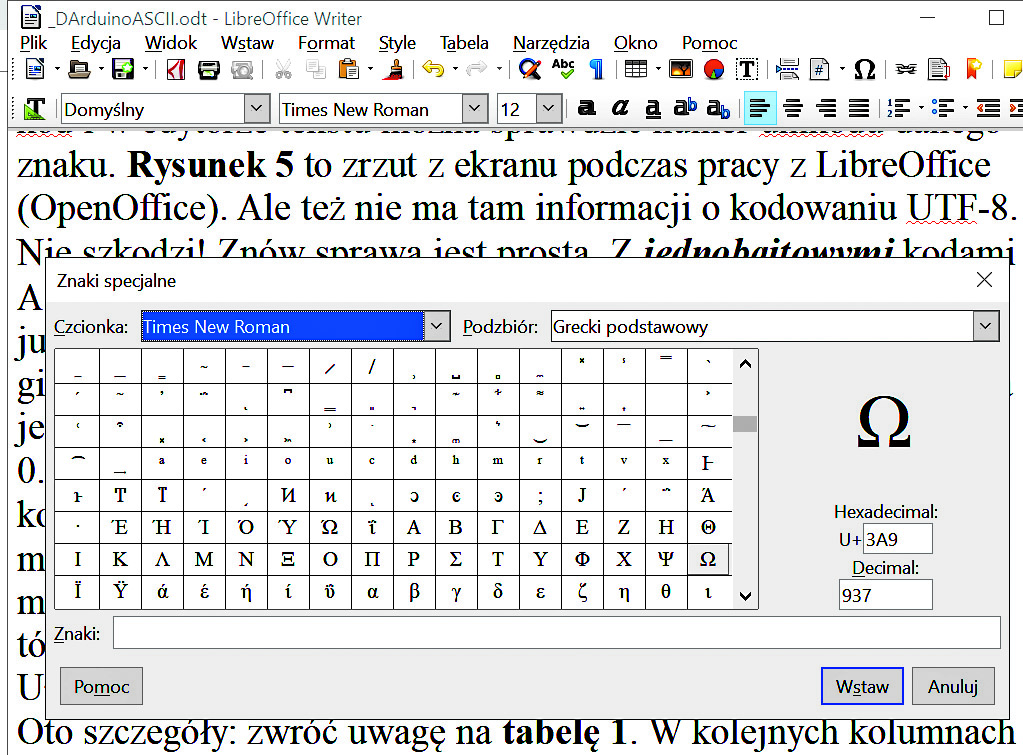
https://unicode-table.com/pl znajdziemy tylko numery unikodu, ale nie ma tam informacji o kodach UTF-8. Także we współczesnych komputerach wykorzystywany jest unikod i w edytorze tekstu można łatwo sprawdzić numer unikodu danego znaku. Rysunek 5 to zrzut z ekranu podczas pracy z LibreOffice (OpenOffice). Ale też nie ma tam informacji o kodowaniu UTF-8.

Nie szkodzi! Znów sprawa jest dość prosta. Z jednobajtowymi kodami ASCII w ogóle problemu nie ma. W kodach dwubajtowych, jak już wiemy, trzy pierwsze bity w pierwszym bajcie i dwa w drugim są zawsze te same. Z szesnastu bitów pozostaje jedenaście, a jedenaście bitów pozwala zapisać liczby dwójkowe w zakresie 0…2047, czyli w zapisie dwójkowym 0…11111111111, szesnastkowo 0…7FF. Nietrudno się więc domyślić, że w dwóch bajtach można zakodować znaki unikodu o numerach do U+7FF, natomiast dla wyższych numerów potrzeba trzech albo czterech bajtów. Wszystkie polskie litery mają numery unikodu niższe niż U+7FF, więc są kodowane w dwóch bajtach.

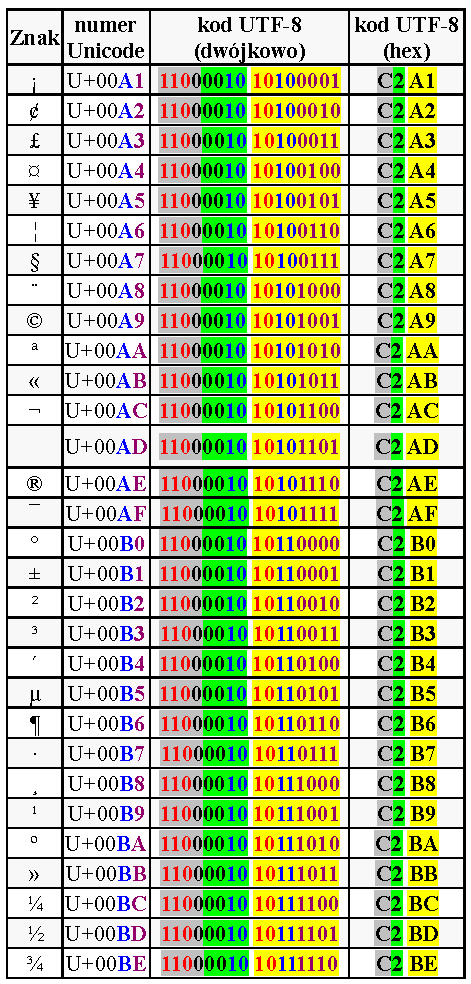
Oto szczegóły: zwróć uwagę na tabelę 1. W kolejnych kolumnach mamy wygląd znaku, jego unikod (szesnastkowo), a dalej dwie postacie kodu UTF-8 (dwójkową i szesnastkową). Kolory ułatwiają rozszyfrowanie struktury i zasad kodowania. Zielone i żółte podkładki pokazują związek między postacią dwójkową i szesnastkową. Bity zaznaczone kolorem czerwonym spełniają podstawowe zasady dwubajtowego kodowania UTF-8. Niebieskie oraz fioletowe cyfry szesnastkowe w numerze Unicode odpowiadają czterem „niebieskim” i czterem „fioletowym” bitom w dwójkowej postaci kodu UTF-8. Jeśli dwójkowy numer unikodu jest krótszy niż 11 bitów, najstarsze bity są wypełniane zerami („czarne zera” w tabeli 1).

Rozpatrzmy szczegółowo przykład

Grecka mała literka mi ma w unikodzie numer U+00B5. Szesnastkowa liczba B5 to dwójkowo liczba ośmiobitowa 10110101. W UTF-8 do zakodowania ośmiobitowego numeru potrzebne są dwa bajty, z których, jak wiemy, pierwszy musi mieć na początku dwie jedynki i zero, a drugi jedną jedynkę i zero. Ośmiobitowa liczba – numer unikodu 10110101 – ma być umieszczona w pozostałych jedenastu bitach obu bajtów, więc dodatkowo na jej początku trzeba dopisać trzy zera: 00010110101. Wtedy można już zestawić ciąg 16 bitów:

11000010  10110101. Mamy tu dwa bajty, z których pierwszy 11000010 w postaci szesnastkowej to C2, a drugi 10110101 to B5. Dwubajtowy kod UTF-8 małej greckiej literki mi (µ) to szesnastkowo: C2  B5.

Niektóre wykorzystywane znaki mają numery wyższe. Przykładowo znak – symbol waluty euro (€) ma unikod U+20AC, czyli dwójkowo 00100000 10101100 (20AC), co wymaga trzech bajtów kodu UTF-8:

11100010  10000010  10101100

a więc trzybajtowy kod UTF-8 symbolu euro ma postać: F2  82  AC. Na rysunku 6 znajdziesz inne popularne przykłady z Wikipedii.

Dla ludzi takie przeliczanie jest nieco kłopotliwe, natomiast dla komputerów – absolutnie nie, bo reguły są bardzo proste. Tabela 1 to drobny fragment strony www.utf8-chartable.de, gdzie wyświetlanie danych można skonfigurować według własnych potrzeb. W razie potrzeby możesz skorzystać właśnie z tej strony.

Jak widzisz, zasady kodowania UTF-8 wbrew pozorom okazują się zaskakująco proste, logiczne. Oprócz pełnej zgodności z ASCII zaletą jest to, że każdy „wyższy”, kilkubajtowy kod (spoza zestawu znaków ASCII) nie zawiera kodu z ASCII (z zerem na początku). To znakomicie zapobiega błędom. Zachowana jest też prawidłowa kolejność sortowania. Teksty zapisane wcześniej z użyciem stron kodowych po przekonwertowaniu na UTF-8 zwykle zwiększają objętość w niewielkim stopniu. Nie ma problemu z kodem równym 0, który nadal może być używany jako znacznik końca łańcucha znaków. Podane reguły mają liczne zalety, między innymi pozwalają na identyfikację, czy jest to kod UTF-8 i likwidują problemy z kolejnością (tzw. sposoby big endian, little endian). UTF-8 ma oczywiście pewne wady, ale też dodatkowe zalety, których nie sposób tu przedstawić. Jeśli chcesz, poszukaj szczegółów w Internecie.

Omawiamy tu dość obszernie podstawy kodowania UTF-8 między innymi dlatego, że realizując projekty Arduino „komunikujące się ze światem”, z pewnością napotkamy problem napisów i kodowania. UTF-8 to dziś podstawowy sposób kodowania tekstu w komputerach i na stronach internetowych. Także konsola tekstowa w pakiecie Arduino IDE wykorzystuje kodowanie UTF-8. Jak już wiemy, inaczej jest ze znakowym wyświetlaczem LCD, który ma dość inteligentny sterownik (HD44780), ale nie „rozumie” kilkubajtowych kodów UTF-8, tylko wszystkie bajty z jedynką na początku traktuje jako znaki o kodach 128…255 ze swojej własnej strony kodowej, która w wyświetlaczach różnych producentów może zawierać inne znaki. Kłopoty i wątpliwości związane są też z wprowadzaniem napisów do Arduino i mikroprocesora. W ramach kursu Arduino stopniowo będziemy poznawać szczegóły, a na razie utrwal sobie informacje o unikodzie i UTF-8. Na zakończenie jeszcze jeden szczegół.

„Surowy tekst”

Na razie mówiliśmy o różnych kodach, które jednoznacznie wiążą liczby ośmiobitowe (0…255) z literami i innymi symbolami graficznymi. Ale mogą one wyglądać różnie. W przypadku małego wyświetlacza znakowego LCD ze sterownikiem HD44780 sprawa jest prosta, bo wygląd znaków/symboli jest określony przez producenta: liczba-kod danej litery powoduje „zaświecenie” określonych punktów-pikseli tworzących daną literę, cyfrę czy inny znak-symbol.

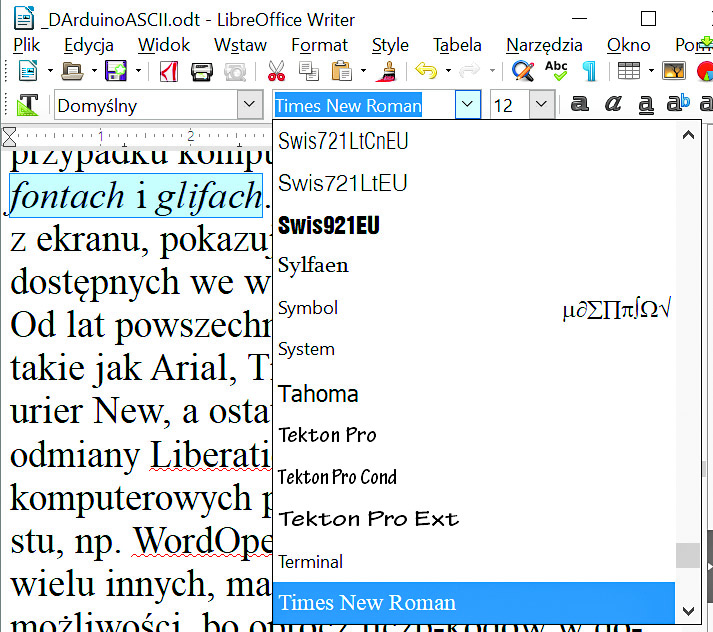
Ale już na ekranie komputera sprawa jest bardziej skomplikowana: ta sama liczba-kod, określająca  przykładowo literkę a, może być wyświetlona w odmienny sposób. Dawniej mówiliśmy o różnych czcionkach, ale czcionka kojarzy się z drukiem i w przypadku komputerów mówimy raczej o fontach i glifach. Na rysunku 7 masz zrzut z ekranu, pokazujący drobną część fontów, dostępnych we współczesnym komputerze. Od lat powszechnie wykorzystujemy fonty takie jak Arial, Times New Roman, Courier New, a ostatnio także Calibri i różne odmiany Liberation. W bardziej złożonych komputerowych programach do edycji tekstu, np. WordOpenOffice, LibreOffice i wielu innych, mamy bogate dodatkowe możliwości, bo oprócz liczb-kodów w dokumencie umieszczane są tam też informacje, jak ma wyglądać dany tekst. Napis o danej treści na ekranie może zostać przedstawiony inaczej, zależnie od wykorzystanego fontu oraz jego odmiany i wielkości. Oprócz omawianego wcześniej kodu wiążącego liczbę ze znakiem-symbolem, w takich przypadkach w grę wchodzą jeszcze inne, dodatkowe informacje, związane z szeroko pojętym formatowaniem. To bardzo obszerna dziedzina, której nie będziemy teraz zgłębiać.

Natomiast w prostych programach komputerowych, np. w Notatniku, Notepad++ oraz w konsoli Arduino, mamy do dyspozycji „jedną gołą czcionkę” – tu liczba-kod jest w prosty i jednoznaczny sposób powiązana z symbolem graficznym (choć w ustawieniach konsoli można wybrać font i jego wielkość na ekranie). Przy programowaniu procesorów zapominamy więc o czcionkach, fontach i glifach, i mówimy tylko o kodzie, który liczby zawarte w komputerze powiąże ze znakami graficznymi (literami, cyframi, itp.), tworząc „zwyczajny, prosty tekst”, dość często nazywany plain text.

W przypadku programowania mikroprocesorów generalnie nie mamy do czynienia z fontami, a tylko właśnie ze „zwykłym tekstem” (plain text), który jest kodowany w stosunkowo prosty sposób. Problemu fontów/czcionek zwykle nie ma w drugą stronę, gdy za pomocą klawiatury do komputera wprowadzamy litery, cyfry i inne znaki graficzne. Wtedy trzeba tylko pamiętać, że zasadniczo do komputera za pomocą klawiatury wprowadzamy kody znaków, a gdy to mają być wartości liczbowe, to nie liczby, tylko oddzielne cyferki (ewentualnie zawierające przecinek lub kropkę). Czy rozumiesz, że to, co wprowadzamy za pomocą klawiatury do komputera czy mikroprocesora, wcale nie jest liczbą, tylko ciągiem znaków? To jest bardzo ważny szczegół, do którego będziemy wracać.

Piotr Górecki