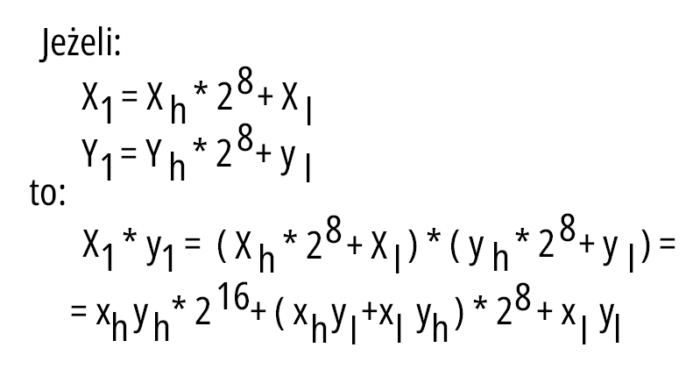Zrozumieć mikroprocesory – operacje mnożenia
Operacje sumowania (odejmowania) realizuje jednostka ALU. Można uznać je za proste działania. Bardziej złożonymi są już operacje mnożenia lub dzielenia. Te są już wykonywane jako ciąg dodawań lub odejmowań. Pierwsze mikroprocesory robiły je programowo, jak one sobie radziły?Kontynuując rozważania dotyczące arytmetyki układów mikroprocesorowych pora rozpocząć działania bardziej złożone. Operacje addytywne (dodawanie, odejmowanie) są wykonywane jakby „w jednym takcie” zegarowym. Inaczej sprawa przedstawia się w działaniach multiplikatywnych (mnożenie, dzielenie). Tu już by uzyskać oczekiwany efekt końcowy koniecznością staje się wykonanie szeregu kroków składających się z działań addytywnych. Obecnie zaawansowane mikroprocesory dysponują rozkazami nakazującymi realizację tych złożonych działań. Prostsze procesory, w szczególności wiele 8-bitowych mikrokontrolerów, musiały realizować te działania programowo.
Mnożenie liczb bez znaku
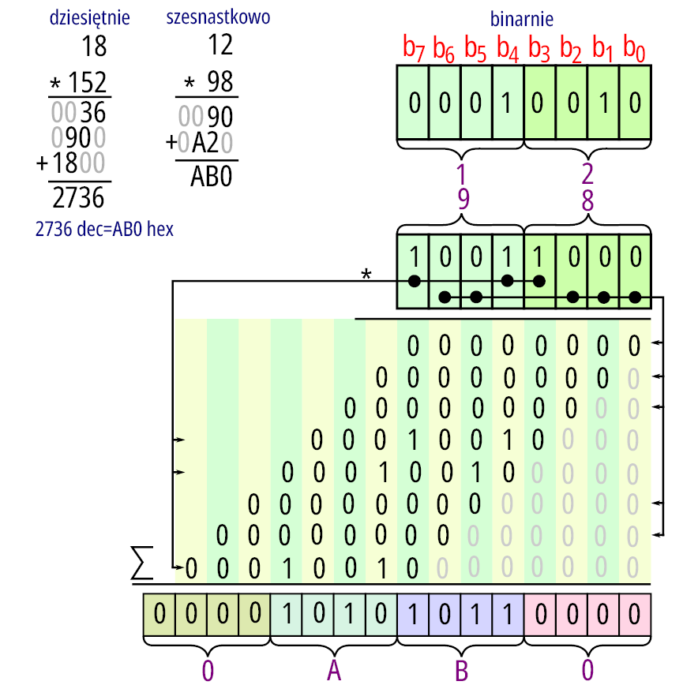
To podstawowa operacja jaką w swojej ofercie muszą mieć mikroprocesory. Sposób jej rozwiązania opiera się na idei mnożenia pisemnego, której każdy z nas musiał się nauczyć w szkole podstawowej. Polega ona na sumowaniu odpowiednio przesuwanych w lewo o jedną pozycję bitową liczb, które są wartością mnożnej lub zerem w zależności od poszczególnych cyfr binarnych mnożnika. Ideę tą dla liczb 8-bitowych w kodzie NB pokazuje rysunek 1.
Wynik mnożenia dwóch liczb 8-bitowych jest liczbą 16-bitową. Wynika to z ośmiokrotnego (z tylu bitów, z ilu składa się czynnik operacji) sumowania liczb przesuwanych arytmetycznie w lewo (co odpowiada mnożeniu przez 2). Wiadomo, że procesory są w stanie przetwarzać liczby większe niż 8-bitowe w operacjach mnożenia. Jak zrobić to dla liczb 16-bitowych? Tu można zaproponować dwie koncepcje realizacji, jedna to identycznie jak dla liczb bajtowych, wykonać działania w zakresie liczb 16-bitowych. Wymaga to już 32-bitowych rejestrów na wyniki pośrednie i wynik końcowy oraz 16 operacji dodawania liczb 32-bitowych. Pamiętając z poprzedniej części, że dodawanie 32-bitowe wymaga zwykłego dodawania oraz trzech dodawań z uwzględnieniem przeniesienia C, robi się już całkiem sporo operacji. Można zaproponować inne rozwiązanie. Liczbę 16-bitową można zapisać jak pokazuje rysunek 2, gdzie:
-
- yh, xh – to starszy bajt liczby 16-bitowej,
- yl, xl – to młodszy bajt liczby 16-bitowej.
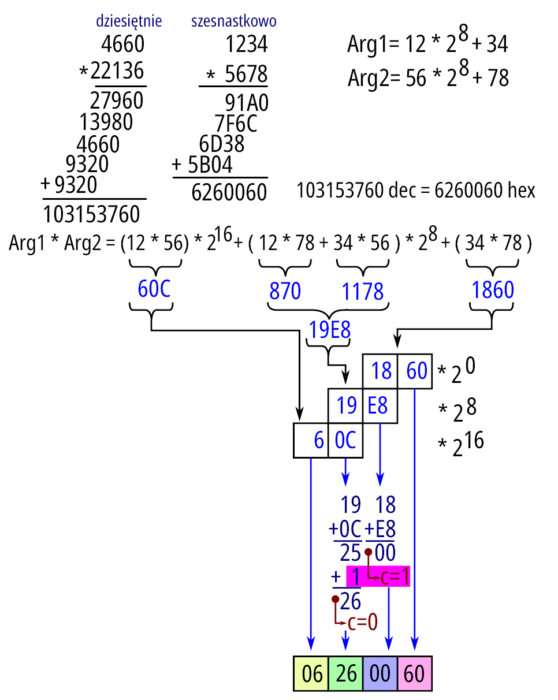
Przykładową realizację mnożenia opartą na tej koncepcji pokazuje rysunek 3. W tym przypadku mamy mnożenie liczby 16-bitowej, bazującej na dostępności jedynie operacji 8-bitowej. Mnożąc 8-bitowo odpowiednie fragmenty liczb i realizując sumowanie odpowiednich części poszczególnych wyników działania, uzyskuje się finalny wynik. Należy tu pamiętać, że przy sumowaniu może wystąpić przeniesienie C, które również należy uwzględnić.
Mnożenie liczb ze znakiem
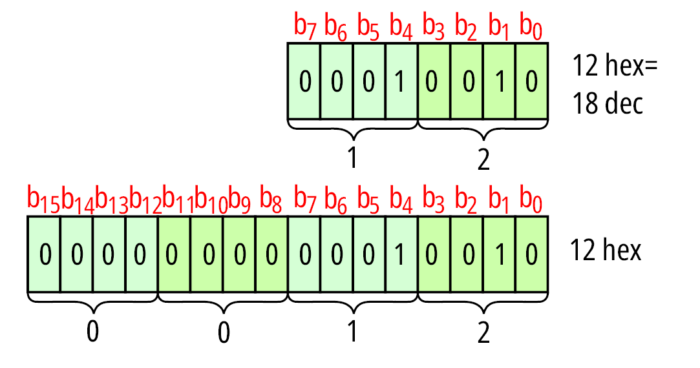
Dosyć podobnie realizowane jest mnożenie liczb w kodzie U2 (liczb ze znakiem). Jak już wspomniałem, wynik mnożenia liczb 8-bitowych mieści się na 16-bitach. To implikuje konieczność rozszerzenia liczb 8-bitowych do postaci liczb 16-bitowych. W przypadku kodu NB jest to wypełnienie starszej części liczby samymi zerami. Taka operacja również musi być wykonana przy mnożeniu liczb w kodzie U2. Tu powstają dwa przypadki: jeżeli liczba jest dodatnia, to jej rozszerzenie do postaci 16-bitowej sprowadza się do wyzerowania starszej części liczby (identycznie jak dla liczb w kodzie NB – przykładową operację pokazuje rysunek 4).
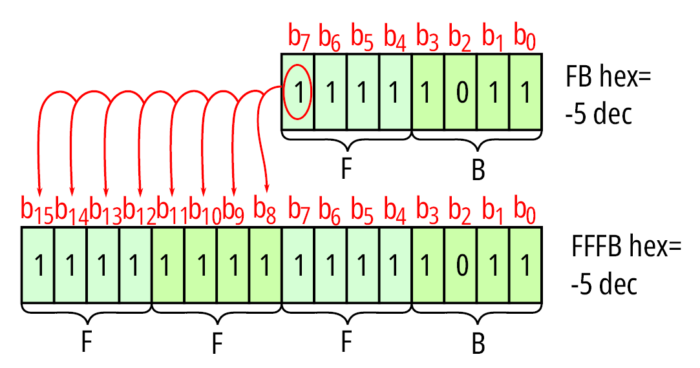
Dla liczb ujemnych należy starszy bajt liczby wypełnić jedynkami – przykład ilustruje rysunek 5. Generalnie powieleniu podlega bit znaku liczby. W obu wariantach wartość liczby nie ulega zmianie.
(…) ciach!
To jest tylko fragment artykułu, którego pełna wersja ukazała się w numerze sierpniowym czasopisma Zrozumieć Elektronikę (ZE 8/2023). Pełna wersja czasopisma umieszczona jest pod tym linkiem. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 8/2023 znajduje się tutaj.
Andrzej Pawluczuk
apawluczuk@vp.pl
Uwaga! Wskazówki, jak nabyć archiwalne numery znajdują się na stronie: https://piotr-gorecki.pl/n11
.