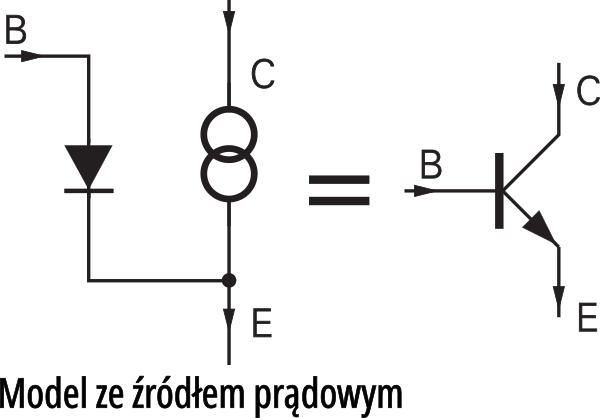Poznajemy tranzystory – część 10

W poprzednich odcinkach zapoznałem cię szeroko z bardzo ważnymi w praktyce parametrami tranzystora, związanymi z jego mocą strat i temperaturami. Już niedługo zajmiemy się kolejnymi zagadnieniami związanymi z tranzystorem. Zapoznasz się z podstawowymi, można powiedzieć − klasycznymi, układami pracy tranzystora w obwodach prądu zmiennego.

W jednym z poprzednich odcinków przedstawiłem ci podstawowe zasady pracy tranzystora w roli przełącznika. Tak się (dziwnie) składa, że wraz z postępem techniki i technologii, w ogóle coraz rzadziej stosujemy pojedyncze tranzystory, a jeśli już stosujemy, to zwykle właśnie w roli elementów przełączających, a nie w roli wzmacniaczy sygnałów zmiennych. Natomiast do wzmacniania sygnałów zmiennych najczęściej stosujemy wzmacniacze operacyjne lub specjalizowane scalone przedwzmacniacze i wzmacniacze mocy audio. Niemniej jednak w podręcznikach szkolnych nadal poświęca się dużo miejsca i uwagi właśnie podstawowym układom pracy tranzystora i co tu ukrywać − większość uczniów ma tego serdecznie dosyć. Niechęć ta jest nawet uzasadniona, bo w praktyce nikt dziś nie projektuje układu wzmacniacza ze wspólną bazą, a co najwyżej jakiś prościutki wzmacniaczyk w układzie wspólnego emitera lub jeszcze prostszy bufor w układzie wspólnego kolektora. I właśnie w takich sytuacjach i ty być może będziesz musiał skorzystać z pewnych informacji podawanych w katalogu. Choć więc generalnie nie będziesz wykorzystywał książkowej wiedzy na temat podstawowych wzmacniaczy przebiegów zmiennych, jednak nie wypada, byś nie znał i nie rozumiał głównych układów pracy tranzystora. Dlatego przynajmniej jeden odcinek będzie poświęcony jedno tranzystorowym wzmacniaczom ze wspólnym kolektorem, wspólnym emiterem i wspólną bazą.

Ale wcześniej muszę cię wprowadzić do pewnego bardzo ważnego zagadnienia. Dlatego w tym odcinku będziemy trochę teoretyzować. Zapoznam cię w niezbędnym zakresie z modelem fizycznym tranzystora, a w następnym artykule zapoznam cię jeszcze z czwórnikami. Dopiero to otworzy ci drogę do zrozumienia parametrów i sposobów opisu spotykanych w katalogach i podręcznikach − a wierz mi, to bywa potrzebne nawet w praktyce hobbysty. Zaciśnij więc zęby i zapoznaj się z tym materiałem, bo musisz to przynajmniej z grubsza rozumieć, o ile tylko naprawdę chcesz być prawdziwym elektronikiem. I obiecuję ci, że przedstawię tu niezbędne minimum − informacje naprawdę konieczne do zrozumienia i uporządkowania wielu zagadnień poruszanych w podręcznikach i katalogach.

W następnej części znów króciutko przypomnimy sobie pojęcie „czarnej skrzynki“. Ale najpierw powrócimy do bardzo uproszczonego modelu tranzystora.

Modele tranzystora

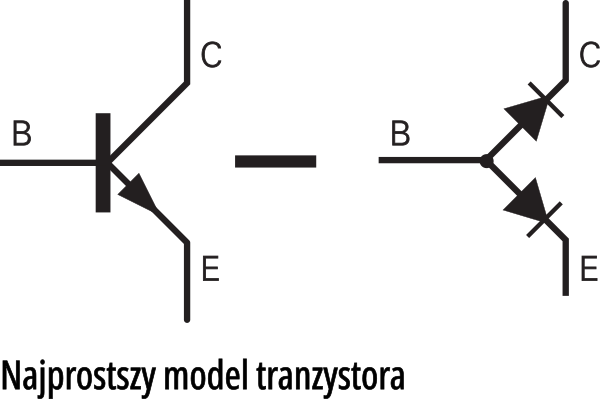
Dowiedziałeś się już (może nawet zmierzyłeś omomierzem), że tranzystor bipolarny to jakby połączenie dwóch diod, jak widać na rysunku 1.

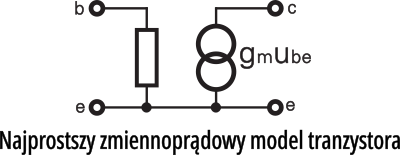
Ale tranzystor to coś więcej niż dwie diody. Swego czasu do znudzenia tłumaczyłem ci pojęcie źródła prądowego i w końcu doszliśmy do wniosku, że działanie tranzystora z grubsza odpowiada działaniu wyimaginowanego układu, pokazanego na rysunku 2. To właśnie jest bardzo prosty, ale jakże przydatny model tranzystora.

Proste? Ale czy to już wszystko?

Właśnie! Nie tak prędko! Bo czy na przykład nasz tranzystor wzmacnia jednakowo napięcia stałe, przebiegi zmienne małej częstotliwości i przebiegi w.cz? Na razie nie wiemy, ale chyba nie… Przecież analizując działanie tranzystora dotychczas rozpatrywaliśmy tylko działanie dla prądów stałych.

Jakiś czas temu tłumaczyłem ci, że gdybyśmy chcieli bardzo dokładnie opisać zachowanie i wszystkie parametry rzeczywistych układów (w tym szczególnie tranzystorów), to musielibyśmy uwzględnić całą masę różnych czynników, z których prawdę mówiąc, niektóre rzeczywiście mają znaczny wpływ, ale inne dają o sobie znać w bardzo małym stopniu. Nie masz chyba wątpliwości, że w praktyce pomijamy te mało znaczące czynniki, upraszczamy zagadnienie i szukamy sposobów na jak najprostsze przedstawienie działania układu. Przyjmujemy uproszczone modele. Takimi modelami są: „czysta“ rezystancja, „czysta“ pojemność, „czysta“ indukcyjność, idealne źródło prądowe czy napięciowe i z ich pomocą utworzyliśmy badzo uproszczony model tranzystora z rysunku 2.

Ten model pokazuje nam z grubsza, jak zachowuje się tranzystor. W tym modelu kluczowymi parametrami są: wzmocnienie prądowe (stosunek prądu kolektora do prądu bazy), które oznaczyliśmy β oraz napięcie przewodzenia złącza baza−emiter. To rozumiesz dobrze.

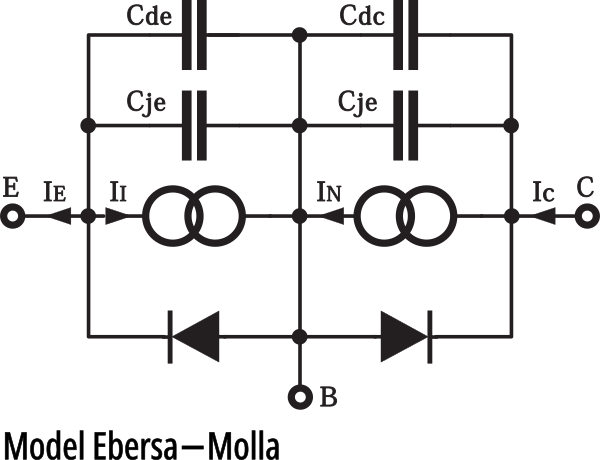
Ale niestety, tranzystor to bardzo kapryśne zwierzę. Nie zdziwisz się więc, że to monstrum, które znajdziesz na rysunku 3 to bardziej precyzyjny model tranzystora.

Jest to tak zwany model Ebersa−Molla (od nazwisk uczonych, którzy go zaproponowali). Na tym modelu znajdziesz dwie znajome „diody“ z rysunku 1 oraz źródło prądowe z rysunku 2. Po chwili zastanowienia uznasz, że rzeczywiście wszystko pasuje, bo spolaryzowaną zaporowo „diodę kolektorową“ na rysunku 2 pominięto. Może trochę zaniepokoi cię drugie źródło prądowe między bazą a emiterem, ale zapewne te dwa źródła można zastąpić jednym pokazanym na rysunku 2. Także zaznaczone pojemności nie wzbudzą wątpliwości − na pewno w dość skomplikowanym tworze, jakim jest tranzystor, występują jakieś pojemności.

Czy mając taki model i opisujące go równania, wiemy już wszyściutko o tranzystorze?

Niestety nie! W głębokiej tajemnicy mogę ci zdradzić, że nawet ten dość złożony model z rysunku 3 (wraz z opisującymi go równaniami matematycznymi) też nie przedstawia calusieńkiej prawdy o tranzystorze. Na przykład w programach komputerowych stosowany jest ulepszony model, zwany modelem Gummela−Poona, ale i on nie jest doskonały.

Co prawda znamy fundamentalne prawa fizyki, na których opiera się działanie tranzystora i znamy też równania matematyczne dokładnie opisujące działanie tranzystora, ale są to (uważaj!) nieliniowe równania drugiego rzędu z pochodnymi cząstkowymi, które nie mają ogólnego rozwiązania, a po ich linearyzacji rozwiązania mają bardzo złożoną postać szeregów nieskończonych.

Niewesoła historia!

Właśnie dlatego koniecznością jest stosowanie modeli uproszczonych. Na ile uproszczonych? To oczywiście zależy już od dokładności wyników obliczeń, jakie chcemy uzyskać oraz od warunków pracy tranzystora. Jeśli chcemy sprawdzić, czy tranzystor nie jest uszkodzony, to wykorzystujemy model z rysunku 1 i omomierzem sprawdzamy, czy między danymi dwoma końcówkami płynie prąd, czy nie. Model z rysunku 2 okazał się pożyteczny przy obliczaniu prostych układów przełączających. Model z rysunku 3 i podobne są wykorzystywane w programach symulacji komputerowej.

Wszystko jasne. A teraz mam dla ciebie kolejną ważną sprawę. Ważną, a zupełnie nie rozumianą przez większość początkujących, którzy od początku są przerażeni stopniem trudności zagadnienia.

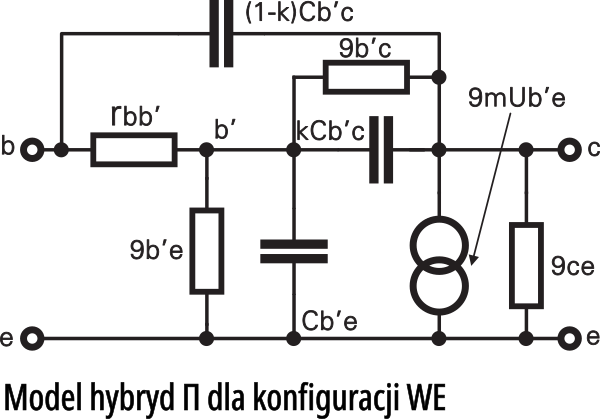
Spójrz na rysunek 4 przedstawiający… Co? No właśnie, według mądrych książek jest to „model hybryd Π tranzystora dla konfiguracji WE“.

I tu właśnie wielu początkujących popada w rozpacz: przecież taki model w niczym nie przypomina łatwego do intuicyjnego pojęcia modelu tranzystora z rysunków 1…3. Czarna rozpacz! Pół biedy, że model jest tak skomplikowany − najgorsze jest to, że nie ma tu żadnych diod, tylko rezystancje, konduktancje (odwrotności rezystancji), pojemności i źródło prądowe. Dlaczego tak jest? Gdzie się podziały diody? Właśnie ten brak diod wprowadza zamieszanie w umysłach początkujących. Głębokie (i słuszne) przekonanie, że w obwodzie baza−emiter występuje przecież dioda, a ściślej złącze półprzewodnikowe, nasuwa wniosek, że oto przekroczono granicę zdrowego rozsądku i wkroczono w dziedzinę elektronicznej czarnej magii.

A więc wobec modelu z rysunku 4 mamy dwa zarzuty: brak diod (złącz) i brak obwodów zasilania.

Temat wcale nie jest taki trudny, jak mogłoby się wydawać na pierwszy rzut oka. Kluczem do jego zrozumienia jest jedno sformułowanie: o ile modele z rysunków 1…3 są ogólnymi (powiedzmy uniwersalnymi) modelami tranzystora, o tyle rysunek 4 pokazuje model dotyczący jedynie prądów zmiennych (ściślej sinusoidalnych o małych amplitudach i niezbyt wielkich częstotliwościach).

W samej rzeczy nie jest to − powiedzmy obrazowo − model „gołego“ tranzystora. W tym wypadku model przedstawia zachowanie tranzystora odpowiednio zasilanego i spolaryzowanego. Właśnie dlatego, że jest to model słuszny tylko dla sygnałów zmiennych. Obwody zasilania i polaryzacji muszą wystąpić w każdym realnym wzmacniaczu, ale tu chodzi o model przedstawiający zachowanie tranzystora dla przebiegów zmiennych, więc obwody te po prostu pominięto. Ot i cała tajemnica!

Dla zakresu wielkich częstotliwości rzędu dziesiątek i setek megaherców wykorzystuje się jeszcze inny model tranzystora, słuszny oczywiście dla przebiegów o wysokiej częstotliwości, i tak− że nie uwzględniający jakichkolwiek obwodów prądu stałego.

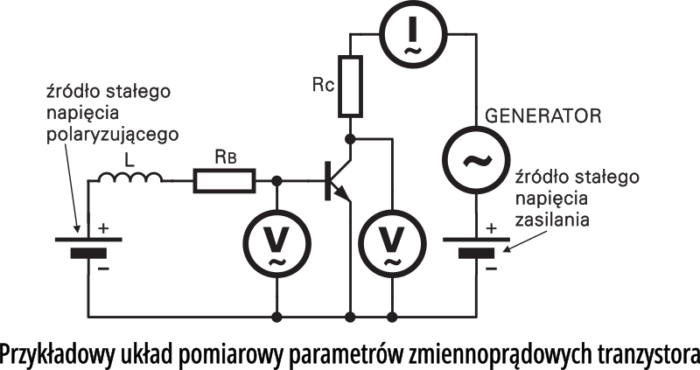
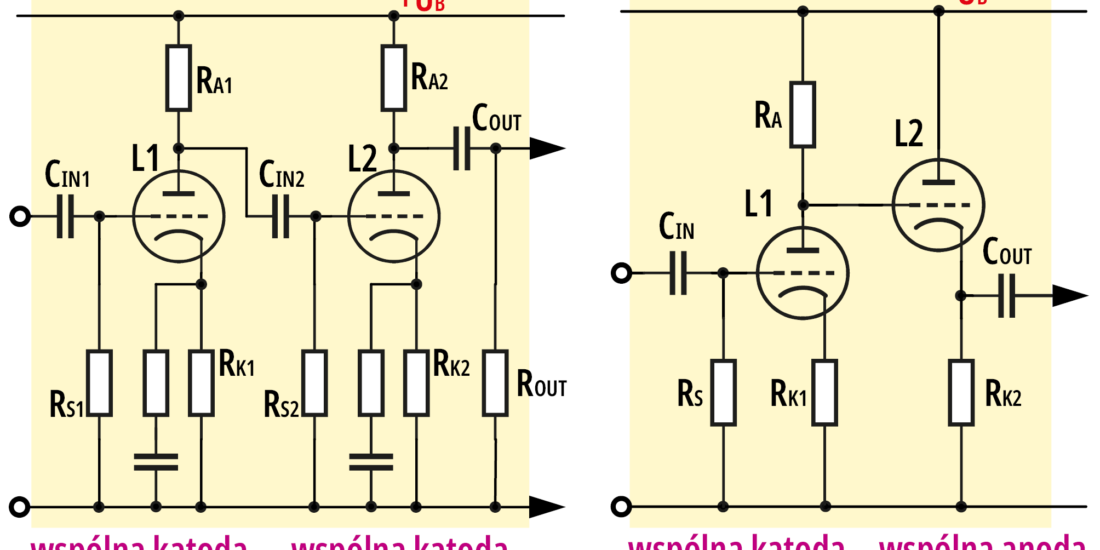
No właśnie, to trzeba wiedzieć: modele takie, jak na rysunku 4 (i modele czwórnikowe, o których opowiem ci w następnym odcinku) pokazują właściwości tranzystora spolaryzowanego, dla pewnego określonego punktu pracy i sterowanego małym sygnałem. Patrząc więc na model z rysunku 4 zawsze powinieneś mieć świadomość, że w rzeczywistości dotyczy on tranzystora pracującego w układzie mniej więcej takim, jak na rysunku 5 (lub podobnym).

Wyjaśniliśmy oto brak obwodów zasilania − trochę trudniej pójdzie z wyjaśnieniem braku diod (złącz). Słusznie podejrzewasz, że w modelu z rysunku 4 diodę zastąpiono rezystancją (ściślej konduktancją, co niczego nie zmienia). Czy wolno tak robić?

Musimy wrócić do charakterystyki diody. Jaką rezystancję ma dioda?

No jaką? Spróbuj samodzielnie odpowiedzieć na to pytanie!

Masz rację! W zasadzie mówienie o jednej konkretnej rezystancji diody nie ma sensu. Rezystancję słusznie możemy określić jako stosunek napięcia do prądu: R = U / I

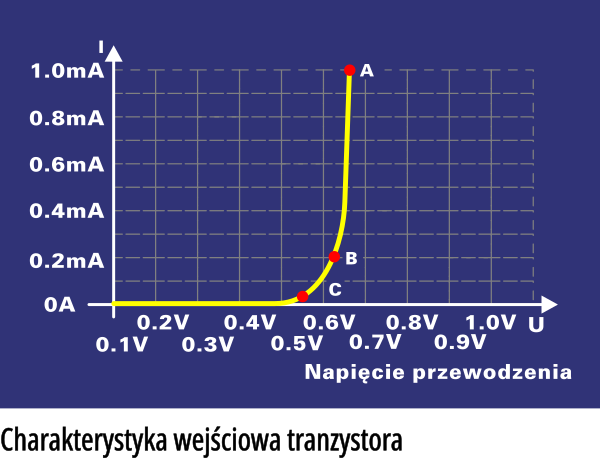
Na podstawie rysunku 6 możesz przybliżeniu obliczyć rezystancję diody dla kilku punktów pracy (napięć i prądów), oznaczonych A, B, C.

Dla A RA = 0,66 V/1 mA = 660 Ω
Dla B RB = 0,613 V/0,2 mA = 3,065 kΩ
Dla C RC = 0,55 V/0,01 mA = 55 kΩ

Czyli rezystancja diody ogromnie zmienia się (zmniejsza) wraz ze wzrostem prądu. Nie można powiedzieć, że dana dioda ma jakąś jedną, konkretną rezystancję.

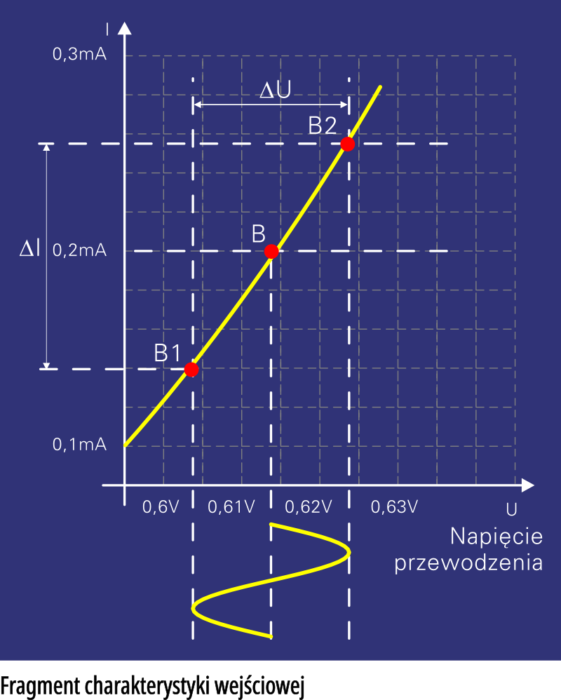
Ale teraz spójrzmy na zagadnienie z trochę innej strony. W tym odcinku wykazałem ci, że jeśli tranzystor ma wzmacniać sygnały zmienne, to musi on być odpowiednio spolaryzowany. Inaczej mówiąc, między bazą a emiterem musi występować jakieś napięcie stałe (około 0,6 V), które wywoła jakiś niewielki stały prąd bazy. Dopiero na takie polaryzujące napięcie stałe zostaje nałożone niewielkie napięcie zmienne, co oznacza niewielką modulację prądu bazy. Rysunek 7 pokazuje w powiększeniu kawałek charakterystyki z rysunku 6. Przypuśćmy, że obwód polaryzacji dostarcza prądu 0,2 mA i napięcie baza−emiter U_BE wynosi 0,613 V.

Teraz bardzo uważaj − jeśli na stałe napięcie polaryzujące zostanie nałożony niewielki przebieg zmienny (na rysunku 7 jest to przebieg o amplitudzie 10 mV), to chwilowy punkt pracy diody (złącza) będzie oscylował pomiędzy punktami B2 i B1. Zauważ, że przy tak małych zmianach napięcia między bazą a emiterem dla uproszczenia możemy śmiało przyjąć, że ten wykorzystywany kawałek charakterystyki jest linią prostą. A jeśli linią prostą, to znaczy że układ się zachowuje tak, jakby tam była rezystancja (bo właśnie rezystancja daje na wykresie linię prostą). Co z tego wynika?

Przy ustaleniu spoczynkowego punktu pracy tranzystora w punkcie oznaczonym B i przy niewielkim sygnale, w uproszczonym modelu rzeczywiście możemy pominąć diodę i potraktować ją jako rezystancję i zamiast modelu z diodą z rysunku 2, możemy więc narysować prostszy model z rezystancją, cały czas pamiętając, że dotyczy to jednego, jedynego punktu pracy i małych sygnałów zmiennych (w naszym przypadku dotyczy prądu bazy równego 0,2 mA i odpowiadającego mu β−razy większemu prądu kolektora). Taki model znajdziesz na rysunku 8.

Czy to zrozumiałeś?

Jeśli tak to świetnie, jeśli nie, czytaj dalej, a potem powróć do ostatniego fragmentu jeszcze raz.

Najpierw ważne pytanie: czy wartością tej zastępczej rezystancji jest obliczona wcześniej „rezystancja“ diody dla punktu B (około 3 kΩ)?

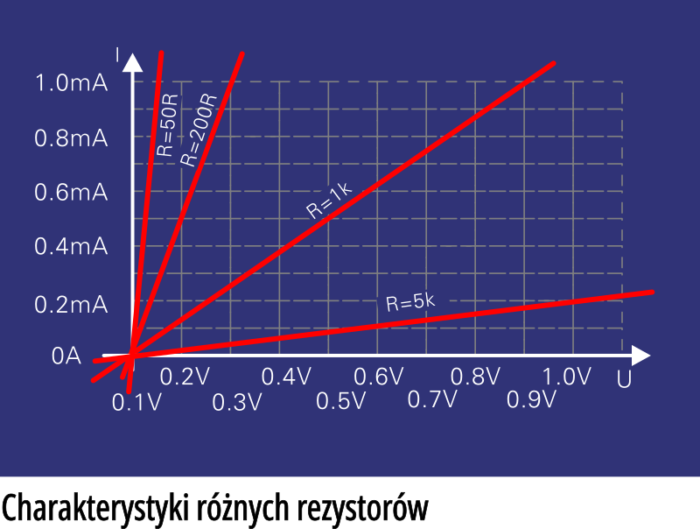
I ten temat musisz bardzo dobrze rozumieć, dlatego na rysunku 9 narysowałem ci analogiczne wykresy dla kilku rezystorów. Sprawa jest jasna: wartość rezystancji jest nieodłącznie związana z (uważaj!) nachyleniem prostej na wykresie. Czy nachylenie prostoliniowego kawałka charakterystyki z rysunku 7 wskazuje na rezystancję obliczoną wcześniej dla punktu B?

Niestety nie!

Zauważ, że wszystkie linie na rysunku 9 przechodzą przez początek układu współrzędnych. Natomiast gdybyś przedłużył prostoliniowy odcinek charakterystyki z rysunku 7, to uzyskana linia na pewno nie przejdzie przez początek układu (punkt 0 V, 0 A). Jak to rozumieć?

Wychodzi na to, że mamy do czynienia z dwoma rezystancjami: jedną obliczoną poprzednio (stosunek napięcia i prądu), drugą wynikającą z nachylenia odcinka charakterystyki.

Pierwszą z nich nazywamy rezystancją statyczną. Tu nie ma wątpliwości. Jest to stosunek napięcia stałego do prądu stałego.

Druga to rezystancja dynamiczna. Dynamiczna, bo dotyczy sygnału zmiennego. Jeśli w szkole uczyłeś się o pochodnych, to masz tu praktyczny przykład ich zastosowania. Jeśli się nie uczyłeś lub już zapomniałeś, pokażę ci to w sposób uproszczony. Nieprzypadkowo na rysunku 7 zaznaczyłem punkty: B1 i B2. Zauważ, że przy zmianie napięcia o ΔU (20 mV), prąd zmienia się o ΔI (około 0,115 mA). Mamy tu przyrosty (zmiany) napięcia i prądu, ale nic nie stoi na przeszkodzie, by zastosować do nich wzór na rezystancję.

Napiszemy: ΔU / ΔI =

no właśnie, równa się czemu? Równa się rezystancji dynamicznej, inaczej różnicowej, a nawet różniczkowej. Żeby ją odróżnić od poprzednio obliczanej rezystancji statycznej, oznaczamy ją małą literą r, nie dużą R. Zapamiętaj tę umowę − często dla uniknięcia niejasności i pomyłek, wielkości dotyczące przebiegów zmiennych oznaczamy małymi literami, a dotyczące stałych napięć, prądów, rezystancji, itp. − dużymi literami.

Możesz bez większego trudu obliczyć, że wartość rezystancji dynamicznej r w punkcie B z rysunków 6 i 7 wynosi około:

r = 20 mV / 0,115 mA = 174 Ω, co znacznie różni się od poprzednio obliczonej dla tego punktu rezystancji statycznej R, wynoszącej około 3 kΩ. Tu na marginesie wyjaśnienie: dla elementów liniowych (np. rezystora), rezystancja dynamiczna i statyczna są równe. Rozróżniamy je tylko w przypadku elementów nieliniowych. A potem mówimy, że rezystancja widziana dla prądu stałego wynosi X omów, a rezystancja widziana dla prądu zmiennego wynosi Y omów. Przyzwyczaj się do takich sformułowań, bo jeszcze się z nimi spotkasz.

Teraz już chyba rozumiesz, dlaczego w modelu dotyczącym małych przebiegów zmiennych można zamiast diody narysować rezystor − spolaryzowana jakimś prądem dioda (złącze) dla małych napięć zmiennych stanowi jakąś konkretną rezystancję. Jeśli przebieg zmienny będzie znacznie większy, nie powinniśmy stosować uproszczeń, zakładając że charakterystyka jest liniowa. Wtedy musimy uwzględnić krzywiznę charakterystyki wejściowej i do ewentualnych wzorów podstawiać wyrażenie matematyczne opisujące naszą krzywą charakterystykę. Oczywiście koszmarnie skomplikowałoby to obliczenia, więc nawet się do tego nie dotkniemy. W praktyce praca ze zbyt dużym sygnałem wejściowym oznacza po prostu pojawienie się na wyjściu zniekształconego sygnału (tu widzisz, dlaczego takie zniekształcenia nazywa się nieliniowymi − bo wynikają z nieliniowości charakterystyki wzmacniacza). Uff, to już prawie koniec!

Być może jednak umknęła twojej uwadze jeszcze jedna pozorna trudność, wprowadzająca w błąd początkujących: jeśli mówimy o prądach zmiennych, to dlaczego na schemacie zastępczym nadal rysujemy źródło prądowe? Przecież kiedyś tłumaczyłem ci, że jest to źródło prądu stałego i prawdopodobnie głęboko utrwaliłeś sobie podane przeze mnie jego wyobrażenie.

Mam nadzieję, że nie sprawi ci kłopotu wyobrażenie „zmiennego“ źródła prądowego. Niewiele tu nowego − w takim źródle prąd okresowo zmienia wartość i kierunek. Przemyśl wiec teraz tę sprawę i przyzwyczaj się do myśli, że zmiennoprądowe źródła prądowe są tak samo naturalne i potrzebne w naszych teoretycznych rozważaniach, jak źródła stałoprądowe. Oczywiście w modelu z rysunku 4 oraz 8 występuje zmiennoprądowe źródło prądowe.

Na sam koniec jeszcze jedno zagadnienie. Nie pomijaj tego materiału, na pewno powinieneś o tym wiedzieć.

Parę słów o tym, jak z lekkostrawnego modelu pokazanego na rysunku 8 robi się model z rysunku 4.

Model z rysunku 2 oraz 8 sugeruje, że działanie tranzystora jest beznadziejnie proste i że prąd kolektora zależy jedynie od prądu bazy (napięcia baza− emiter). Już ci mówiłem, że tranzystor to kapryśne zwierzę. Nie będę cię tu katował rozważaniami na temat wstrzykiwania nośników, modulacji szerokości bazy czy zmian pojemności dyfuzyjnej i złączowej pod wpływem zmian napięcia kolektora.

W każdym razie w bardziej precyzyjnym modelu źródło prądowe nie jest idealne, a ponadto występują nikomu niepotrzebne i wręcz szkodliwe pojemności oraz szkodliwa rezystancja obszaru bazy, a na dodatek to co dzieje się na wyjściu (zmiany napięcia kolektora) w zauważalnym stopniu wpływa na obwody wejściowe (czyli występuje swego rodzaju wewnętrzne sprzężenie zwrotne z wyjścia na wejście).

I właśnie poszczególne elementy na rysunku 4 reprezentują te niepożądane zjawiska. Widzisz, jak ktoś to wszystko sprytnie wykombinował?

Przy okazji analizy rysunku 4 − w obliczeniach teoretycznych bardzo często dla wygody zamiast rezystancją R lub r posługujemy się konduktancją G lub g, czyli przewodnością, która jak wiesz jest odwrotnością rezystancji. Może ci się to wyda dziwne i myślisz, że to utrudnienie. Jednak przy różnorodnych dość skomplikowanych obliczeniach jest to nawet pewne ułatwienie. I nie myśl, że ta konduktancja (i później admitancja) to coś potwornie trudnego do intuicyjnego pojęcia − po pewnym czasie także ty byś się przyzwyczaił i jednakowo dobrze rozumiał czy wyczuwał sens rezystancji i konduktancji. Dlatego nie przejmuj się tym że na rysunkach znajdziesz zarówno rezystancje (dynamiczne) r, jak i konduktancje (i transkonduktancje) g. Powiem więcej − na tym poziomie rozważań, na którym jesteśmy, nic się nie stanie, jeśli nawet pomylisz konduktancję z rezystancją. A sprawa wspomnianej transkonduktancji (oznaczonej gm) wyjdzie nam w całym swym blasku, gdy będziemy analizować działanie tranzystorów polowych.

Mógłbym ci jeszcze zasygnalizować lub nawet wyjaśnić kilka dalszych zagadnień związanych z omówionymi modelami tranzystora, ale przecież ustaliliśmy, że nie jest to systematyczny kurs teoretyczny, tylko mam ci nakreślić ogólny obraz, byś rozumiał z grubsza, o co chodzi w katalogu. Dlatego ten odcinek kończymy, a w następnym odcinku powrócimy do czarnej skrzynki i porozmawiamy o czwórnikach, modelu zaciskowym i wreszcie wyciągniemy praktyczne wnioski ze zdobytej wiedzy.

Piotr Górecki