Pierwsze kroki w cyfrówce – część 16

W poprzednim odcinku zapoznałeś się z ogólnie z licznikami  i dzielnikami. W tym odcinku przedstawione są sposoby skracania cyklu zliczania. Sposoby takie są stosowane w większości liczników dziesiętnych.

Liczniki dziesiętne

A teraz kolejna istotna sprawa. Najpierw wydawało ci się, że liczniki nierozerwalnie związane są z kodem dwójkowym, potem namieszałem ci jakimś tam „dżonsonem”, który nie dość, że jest jakby rejestrem, to jeszcze daje na wyjściu swego wewnętrznego dekodera nie kod dwójkowy, tylko tak zwany kod 1 z 10 (jeden z dziesięciu). Prawdopodobnie nurtuje cię jednak pytanie, jak to jest z licznikami liczącymi do dziesięciu. Czy do realizacji licznika dziesiętnego trzeba używać „dżonsona”? Przecież stany na jego wyjściach nie mają praktycznie nic wspólnego z liczbami 0…9 zapisanymi w kodzie dwójkowym.

Kiedyś, gdy byłem jeszcze bardzo młody, gdy pojawiały się pierwsze cyfrowe zegarki i elektroniczne kalkulatory (takie ze świecącymi na czerwono wyświetlaczami LED), wiedziałem już, że wszystkie układy cyfrowe, także w zegarkach i kalkulatorach, wykorzystują kod dwójkowy. Zastanawiałem się długo, jak „oni to zrobili”, że dwójkowy licznik zlicza do dziesięciu, a dwa takie liczniki mogą zliczać do dwunastu, dwudziestu czterech, czy sześćdziesięciu. Było to dla mnie nieprzeniknioną tajemnicą. Może i ty, młody Czytelniku masz podobny problem. Jeśli tak, dokładnie zapoznaj się z poniższymi informacjami.

Prostym sposobem uzyskania licznika zliczającego do 10 jest po prostu skrócenie cyklu zliczania licznika czterobitowego. Czterobitowe liczniki zliczają do 16. Do szesnastu? Tu niektórzy zaprotestują! Ściśle biorąc, czterobitowe liczniki dwójkowe (binarne) mają 16 różnych stanów wyjściowych, a najwyższą zawartością jest liczba 15, czyli 1111_B. Tak jest! Nigdy nie zapominaj, że w elektronice i informatyce zliczanie zaczyna się od zera, a nie od jedności.

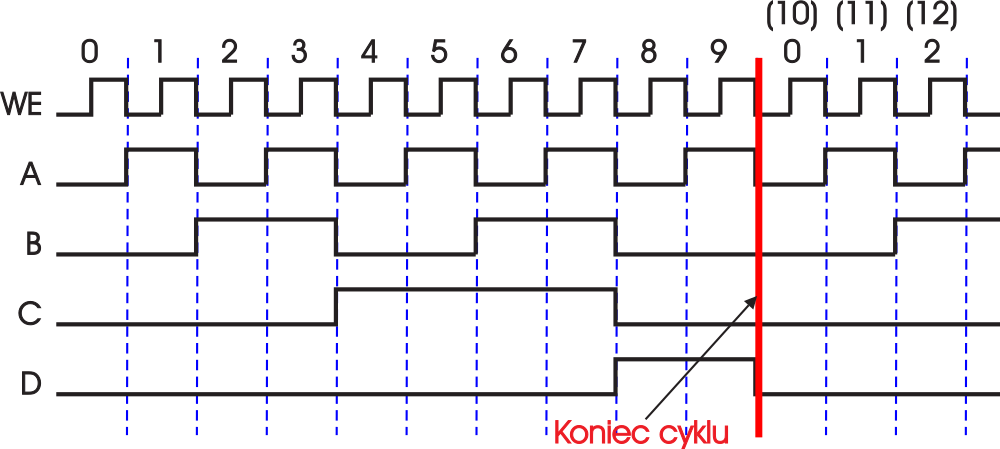
Stąd oczywiście jeśli licznik ma mieć dziesięć stanów wyjściowych, to trzeba skrócić cykl pracy, by licznik liczył od 0 do 9, a potem znów zaczynał od zera. Na rysunku 1 możesz zobaczyć oczekiwane stany licznika. Tylko jak skrócić cykl, by po liczbie 9 (1001_B) pojawiła się liczba zero (0000_B)?

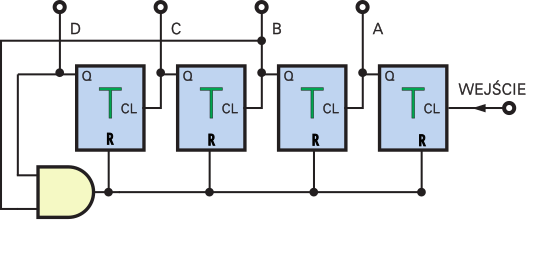
Zasada jest prosta: w momencie, gdy licznik przechodzi do następnego stanu, czyli liczby 10 (1010_B), wszystkie przerzutniki zostają wyzerowane i cykl pracy rozpoczyna się od nowa. Jedno z najprostszych rozwiązań pokazane jest na rysunku 2. Bramka AND pełni rolę dekodera, wykrywa pojawienie się w liczniku liczby 1010_B, i zeruje przerzutniki. Proste?

Może zastanawiasz się, dlaczego występuje tu tylko dwuwejściowa bramka AND? Przecież zerowanie nastąpi nie tylko po pojawieniu się liczby 1010_B, ale także 1011_B, 1110_B, 1111_B. Wpadłeś kolego! Przecież jeśli licznik zlicza w przód, to nie ma siły – najpierw pojawi się liczba 1010_B i licznik zostanie wyzerowany. Żadna z liczb: 1011_B, 1110_B, 1111_B wcale nie pojawi się w liczniku w czasie normalnej pracy (choć może przypadkowo „wskoczyć” po włączeniu napięcia zasilającego – zastanów się samodzielnie, jak to wpłynie na cykl pracy licznika).

No i co?

Czy już zrozumiałeś, w jak prosty sposób można z klasycznego licznika dwójkowego wykonać licznik o dowolnie krótszej długości cyklu? Czy już wiesz, jak zrobić dzielnik dzielący częstotliwość przez dowolną liczbę? Wystarczy do tego licznik dwójkowy o długości cyklu większej, niż ci potrzeba. Ten licznik musi mieć wejście zerujące. Zasada jest oczywista: jeśli licznik ma zliczać do jakiejś liczby N (a ściślej mieć N różnych stanów wyjściowych, łącznie z zerem), to należy przedstawić liczbę N w postaci dwójkowej, a następnie zbudować prosty dekoder, który wyzeruje licznik w momencie pojawienia się na wyjściach liczby N. Inaczej mówiąc, na wyjściach pojawiać się będą kolejne liczby od zera do N−1, a pojawienie się liczby N momentalnie wyzeruje licznik. Można powiedzieć, że w zasadzie liczba N nie pojawi się w liczniku (w rzeczywistości pojawi się tylko na kilkadziesiąt nanosekund). Zastanów się czy dobrze rozumiesz ostatnie zdanie.

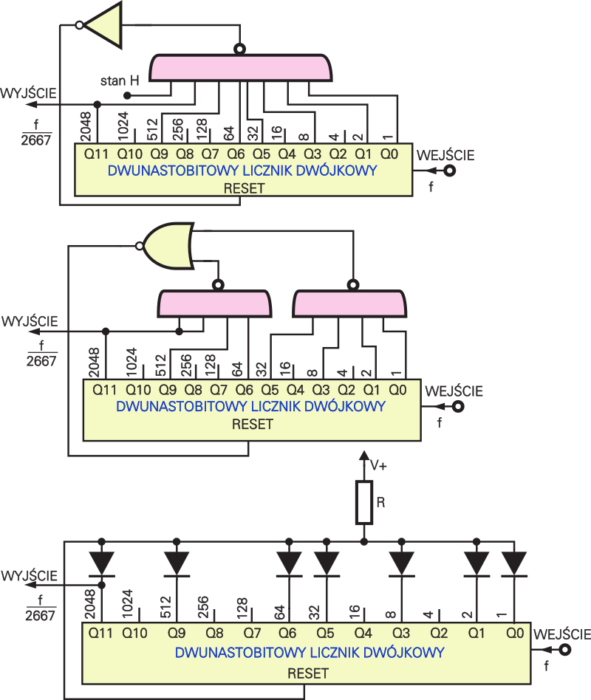
Na rysunku 3 zobaczysz proste sposoby dowolnego skracania długości cyklu liczników asynchronicznych z rodzaju: 4020, 4024, 4040, 4060 i w ogóle wszystkich liczników mających wejście zerujące. Pokazany dwunastobitowy licznik normalnie zlicza do 4096 (0…4095), ale w pokazanym układzie cykl został skrócony do 101001101011_B czyli 2667. W liczniku występują liczby 0…2666, pojawienie się liczby 2667 zeruje licznik. Zgadza się?

Czy dokładnie rozumiesz dlaczego przy ustawieniu dekodera na 2667, licznik zlicza od 0 do 2666? Musisz to dobrze pojąć. No i znów kłania się „oscyloskop w oku”. Czy już widzisz kolejne niebezpieczeństwo?

Jeszcze nie?

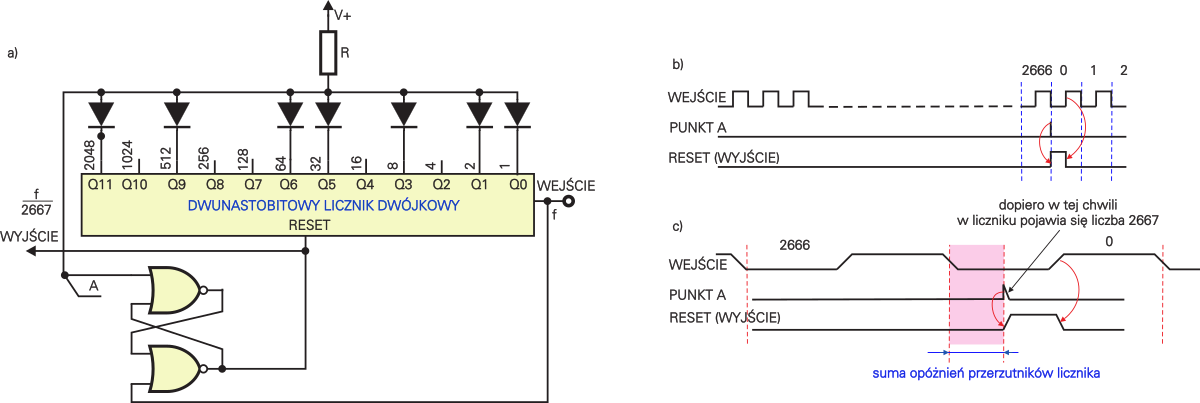
Mądre książki ostrzegają, iż przy takich najprostszych sposobach istnieje pewne ryzyko, że nie wszystkie przerzutniki zostaną należycie wyzerowane. Przecież pojawienie się określonego stanu wy− jściowego (liczby 2667) spowoduje momentalne wyzerowanie licznika i w efekcie stan ten zaniknie z wejścia zerującego dosłownie po kilkunastu czy kilkudziesięciu nanosekundach. Taki króciutki, nanosekundowy impuls może okazać się zbyt krótki do wyzerowania wszystkich stopni licznika. W praktyce sposoby z rysunku 3 zdają egzamin, jeśli cały licznik zawarty jest w tym samym układzie scalonym. Tylko w przypadku, gdy do budowy licznika użyte byłoby kilka połączonych układów scalonych, rozrzuty ich parametrów mogłyby spowodować błędy. Wtedy wspomniane ryzyko można w prosty sposób wyeliminować, stosując przerzutnik RS według rysunku 4a.

Zauważ, że tym razem nie ma ryzyka. Pojawienie się stanu wysokiego w punkcie A ustawia dodatkowy przerzutnik RS (z bramek NOR) i zeruje licznik. Pomimo, że impuls w punkcie A zanika po kilkudziesięciu nanosekundach, przerzutnik nadal jest ustawiony, aż do pojawienia się stanu wysokiego w przebiegu wejściowym. Obejrzysz to na rysunku 4b. Zwróć uwagę, że mamy tu do czynienia z typowym licznikiem asynchronicznym z aktywnym zboczem opadającym. Na rysunku 4b nie zaznaczyłem opóźnienia. Zobaczysz je pod lupą na rysunku 4c. Pamiętaj o tych opóźnieniach, bo ograniczają one maksymalną częstotliwość pracy licznika – stany na wszystkich wyjściach muszą się ustalić przed przyjściem na wejście zegarowe następnego aktywnego zbocza ( układy z rys. 3) lub dodatniej połówki przebiegu (w układzie z rysunku 4). Właśnie tu masz przykład, że ze względu na sumowanie się opóźnień, licznik asynchroniczny będzie miał znacznie mniejszą maksymalną częstotliwość pracy, niż licznik synchroniczny o podobnej pojemności.

A co z błędnymi kodami na wyjściu licznika asynchronicznego? Czy nie spowodują błędnego działania i przedwczesnego skracania cyklu? Coś takiego mogłoby wynikać z rysunku 7a, który znajduje się w poprzedniej części.

Spróbuj udowodnić, że licznik będzie pracował poprawnie pomimo występowania błędnych kodów wyjściowych. To jest dość trudne, więc podpowiem ci: zastanów się, jakie błędne kody będą się pojawiać przy zliczaniu w przód.

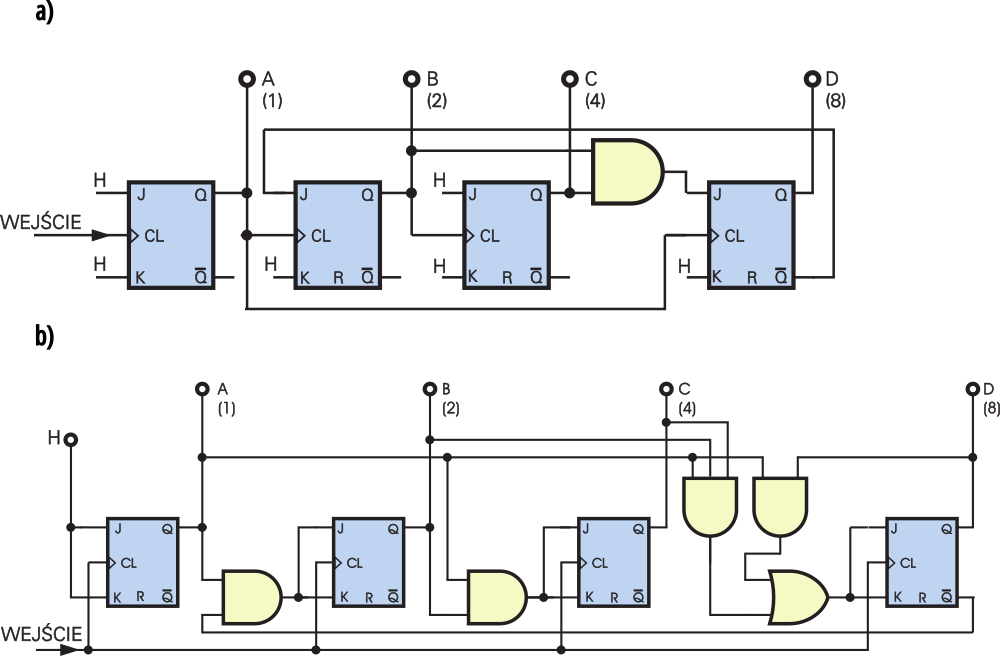
W scalonych licznikach zliczających do dziesięciu stosuje się jeszcze inne sposoby skracania cyklu. Nie musisz ich wcale znać, ale jeśli cię to interesuje, dwa przykłady takich liczników znajdziesz na rysunku 5. Masz tu dekadowy licznik asynchroniczny (rysunek 5a) oraz synchroniczny (rysunek 5b). Zachęcam cię, byś samodzielnie przeanalizował ich działanie i narysował przebiegi. Czy rzeczywiście są to liczniki liczące w kodzie dwójkowym od 0 do 9, mające przebiegi według rysunku 1?

Zgadza się? Nie zdziwisz się zapewne, jeśli dowiesz się, że mniej więcej tak zrealizowane są niektóre liczniki scalone, np. 7490, 74160, 74190 czy 74192.

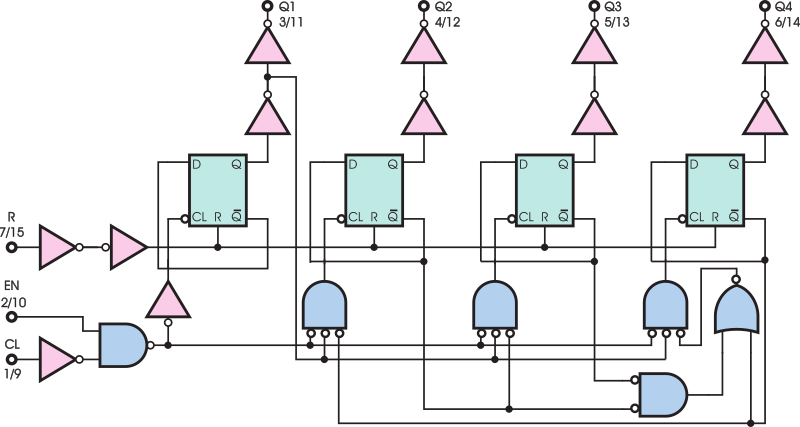
Rysunek 6 przedstawia schemat wewnętrzny bodaj najczęściej używanego licznika dekadowego z rodziny CMOS – kostki 4518. Jak widać, jest to licznik synchroniczny. Możesz spróbować przeanalizować jego działanie, ale nie to jest najważniejsze – chcę ci pokazać kolejną sprawę praktyczną.

Być może już zauważyłeś przeglądając katalog, że sporo liczników CMOS ma jakby podwójne wejście. W zasadzie jedno z tych wejść jest „prawdziwym” wejściem zegarowym, oznaczonym CL lub T, a drugie jest wejściem zezwalającym, oznaczonym zwykle EN od enable – zezwalać lub STROBE. Podanie na wejście EN stanu wysokiego umożliwia zliczanie impulsów podawanych na wejście CL, podanie stanu niskiego na EN uniemożliwia zliczanie, ale nie zeruje licznika. W takim układzie licznik zwiększa swą zawartość przy wystąpieniu na wejściu CL rosnącego zbocza.

Przemyślni twórcy liczników zadbali o to, by licznik mógł zwiększać swą zawartość także przy zboczu opadającym, co jak się za chwilę okaże, jest niezbędne przy łączeniu kilku takich liczników. Tak zaprojektowali obwody wejściowe, by po dołączeniu wejścia CL do masy i podaniu przebiegu na wejście EN, licznik zmieniał stan przy zboczu opadającym. Taką budowę wejścia ma nie tylko kostka 4518 czy bliźniacza 4520, zliczająca do 16. Taki sam obwód wejściowy ma nasz ulubieniec – układ 4017.

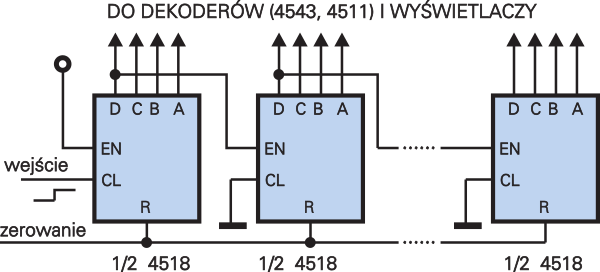
Dla zwiększenia uniwersalności wejście CL zazwyczaj jest wyposażone w układ Schmitta, czyli może pracować także z sygnałami o bardzo łagodnych zboczach. Jeśli chodzi o wejście EN, to katalogi zawierają mętne informacje: z niektórych źródeł wynikałoby, że także na wejściu EN umieszczono układ Schmitta, ale inne źródła o tym nie wspominają. Lepiej przyjąć, że tylko wejście CL wyposażone jest w układ Schmitta. Dlatego pierwszy licznik może i w miarę możliwości powinien zliczać impulsy przez wejście CL, natomiast następne siłą rzeczy muszą wykorzystywać końcówkę EN jako wejście, jak to pokazano na rysunku 7.

Rysunek 7 pokazuje synchroniczne liczniki 4518 połączone są w najprostszy sposób – kaskadowo. W ten sposób choć każdy licznik jest synchroniczny, poszczególne liczniki pracują w sposób asynchroniczny, to znaczy zmiany stanów na ich wyjściach nie następują w jednej chwili, tylko kolejno, w odstępie kilkudziesięciu nanosekund. W ogromnej większości zastosowań nie jest to wadą i układ z rysunku 7 jest najczęściej używanym licznikiem dziesiętnym (z kostkami 4518). Identycznie wygląda schemat licznika z licznikami dwójkowymi 4520, ale tych kostek używa się rzadko, wykorzystując zamiast nich dwójkowe liczniki asynchroniczne, takie jak 4060, 4040 czy 4020.

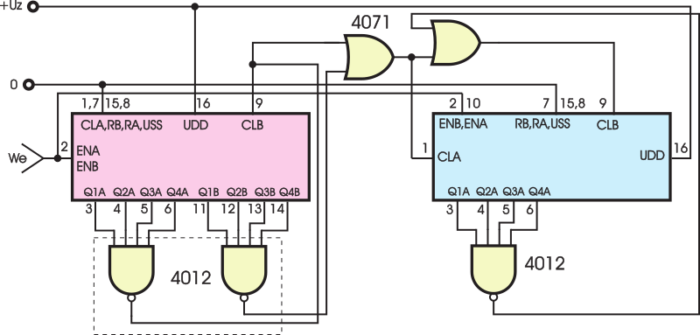
Synchroniczne liczniki 4520 (i 4518) można też łączyć, by cały zespół pracował synchroniczne. Jeśli byłoby to absolutnie konieczne, można wykorzystać układ z rysunku 8.

W tym i poprzednim odcinku oprócz informacji o działaniu liczników, próbowałem cię oswoić z różnymi sposobami oznaczania wejść, wyjść i rysowania schematów. Zwróć uwagę, że rysunek 8 też jest przykładem odmiennego (szczerze mówiąc, trochę niejasnego) narysowania schematu licznika. Porównaj też wcześniejsze rysunki, byś w przyszłości nie zgubił się w rozmaitości oznaczeń i sposobów rysowania.

Tyle podstawowych informacji o licznikach.

A w kolejnym odcinku bliżej zapoznasz się z następnymi popularnymi licznikami dwójkowymi i licznikami BCD.

Piotr Górecki