PKE – Praktyczny Kurs Elektroniki (15) Iluminofonia selektywna
Na fotografii wstępnej pokazany jest model selektywnej, pasmowej iluminofonii, reagujący na dźwięki z zakresu około 70…280 Hz. Powodują one zaświecanie dwóch białych diod LED. Układ zawiera skuteczny filtr pasmowy, który nie tylko przepuszcza, ale też około 10-krotnie wzmacnia sygnały w paśmie przepustowym, a silnie tłumi sygnały o innych częstotliwościach.
W rezultacie układ zupełnie nie reaguje na sygnały o „obcych” częstotliwościach. Wyróżnia się tym spośród typowych układów iluminofonicznych, w których z reguły stosowane są proste i mało skuteczne filtry, reagujące także na silne przebiegi „obce”. W prezentowanym układzie częstotliwość filtru można bardzo łatwo zmieniać przez wymianę czterech jednakowych kondensorów. Czułość iluminofonii można łatwo korygować za pomocą jednego rezystora. Model z fotografii wstępnej ma dużą czułość. Przy głośnej muzyce można zmniejszyć wzmocnienie, usuwając zupełnie R7, a gdyby nadal było za duże, można też zmniejszyć wartość R1.
Opis układu dla „zaawansowanych”
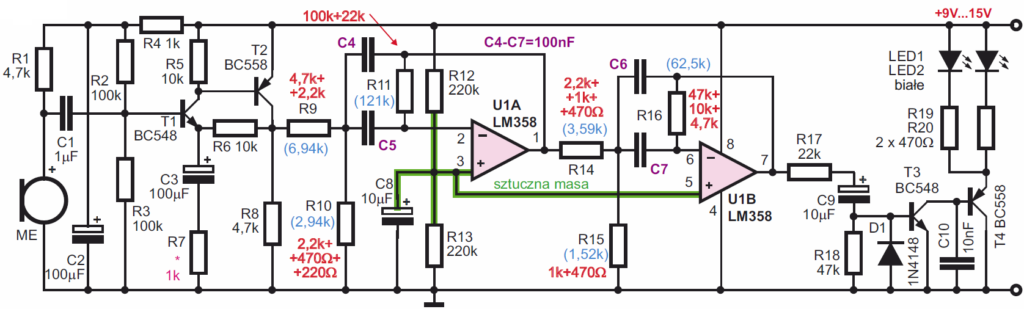
Schemat ideowy jednokanałowej iluminofonii pasmowej pokazany jest na rysunku A. Mikrofon elektretowy ME pracuje w typowym układzie pracy z rezystorem obciążenia R1 i filtrem R4C2. Sygnał z mikrofonu przechodzi przez C1 i jest wzmacniany w przedwzmacniaczu z tranzystorami T1, T2. Wzmocnienie tego stopnia wyznaczone jest przez stosunek rezystorów R6/R7 i można je zmieniać w szerokim zakresie, modyfikując wartość R7 (220 Ω…10 kΩ).
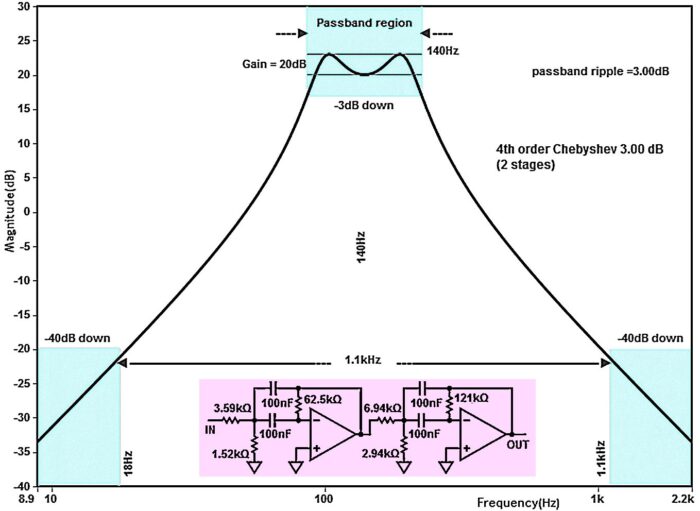
Wzmocniony sygnał podawany jest na dwustopniowy filtr ze wzmacniaczami operacyjnymi U1A i U1B. Jest to filtr pasmowy o częstotliwości środkowej 140 Hz i 3-decybelowym paśmie przenoszenia też wynoszącym 140 Hz. Rysunek B pokazuje charakterystykę amplitudową filtru i jego schemat.
Na rysunku B podane są idealne wartości elementów, wyliczone przez program projektowy. Te wartości są zaznaczone na rysunku A kolorem niebieskim. Odchyłki od tych wartości skutkują nie tylko przesunięciem częstotliwości, ale też zdeformowaniem charakterystyki. W takich filtrach z reguły stosuje się rezystory o tolerancji 1% i kondensatory o możliwie wąskiej tolerancji, najlepiej dobierane. My stosujemy kondensatory C4–C7 nieselekcjonowane, „wprost z pudełka”, a potrzebne wartości rezystancji składamy z dwóch lub trzech rezystorów. Na rysunku A wartości te podane są kolorem czerwonym.
Omawiany dwustopniowy filtr wydziela z odbieranych dźwięków tylko składniki o częstotliwościach ze „swojego” pasma. Sygnały te są podawane przez rezystor R17 i kondensator C9 na rezystor R18 i na aktywny prostownik z tranzystorem T3. Dioda D1 zapewnia symetryczną pracę prostownika. Rezystor R18 jest potrzebny choćby tylko po to, żeby po włączeniu zasilania szybko naładować C9 – by zbyt długo nie świeciły wtedy diody LED.
Jeżeli sygnały zmienne z wyjścia wzmacniacza będą mieć na bazie T3 amplitudę powyżej 0,6 V, wtedy tranzystor ten będzie otwierany w dodatnich szczytach sygnału. Przepływ prądu kolektora T3 otworzy wtórnik na tranzystorze T4 i zaświeci białe diody LED1, LED2. C10 jest filtrem tego aktywnego prostownika. Bez kondensatora C10 diody świeciłyby tylko w dodatnich szczytach sygnału, a jego obecność przedłuża świecenie diod LED. Wartość C10 można zmieniać według upodobania (0 nF…1 uF).
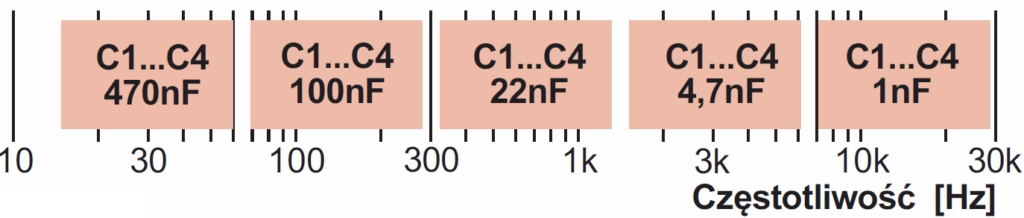
Filtr pasmowy ze wzmacniaczami operacyjnymi U1A, U1B jest tak zaprojektowany, żeby można było łatwo zmienić jego częstotliwość. Wystarczy zmienić jednakowe kondensatory C4…C7. Z kondensatorami o pojemności 100 nF częstotliwość środkowa wynosi około 140 Hz. Zmieniając pojemności na 470 nF, otrzymamy filtr najniższych częstotliwości, reagujący na sygnały z pasma 15 Hz…60 Hz. Wymieniając C4…C7 na 22 nF, otrzymamy filtr o częstotliwości środkowej 640 Hz i paśmie około 320 Hz…1,28 kHz. Z kondensatorami 4,7 nF pasmo wyniesie około 1,5 kHz…6 kHz, a z kondensatorami 1 nF otrzymamy filtr najwyższych częstotliwości o paśmie około 7 kHz…28 kHz. Poszczególne pasma nie zachodzą na siebie – zachowana jest separacja kanałów, co pokazuje rysunek C.
My zastosowaliśmy kondensatory 100 nF. Trzeba też pamiętać, że wzmacniacze operacyjne z kostki LM358 są powolne i nadają się jedynie do filtrów niskich częstotliwości (30 Hz i 140 Hz, najwyżej 640 Hz). Realizując filtry o wyższych częstotliwościach, trzeba zastosować szybsze wzmacniacze operacyjne, a przedwzmacniacz, zamiast na tranzystorach, też można byłoby zrealizować na takim szybkim wzmacniaczu operacyjnym.
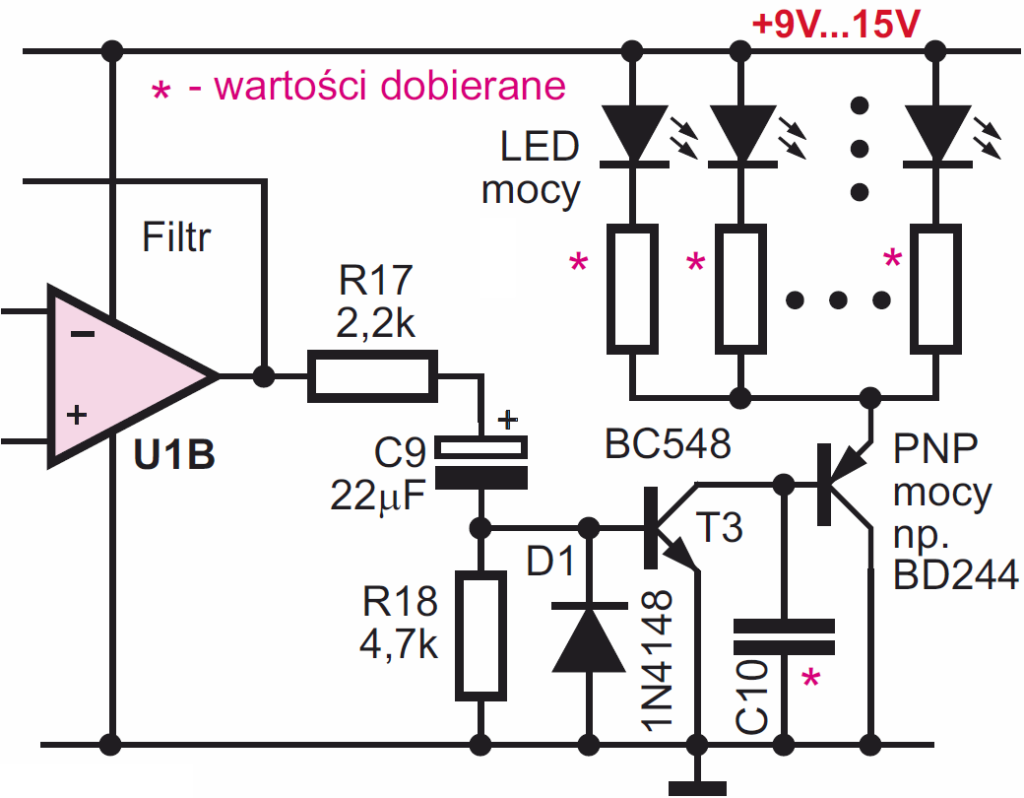
Układ można zmodyfikować, zmieniając wartości elementów prostownika i stosując tranzystor T4 o większej mocy. Wtedy aż prosi się zastosować diody LED o dużej mocy. Taką modyfikację można przeprowadzić według rysunku D, dobierając według upodobania C10 i stosując szeregowe rezystory ograniczające prąd, stosownie do użytych diod LED.
Trzeba też zadbać o skuteczne chłodzenie diod LED mocy – popularne diody w obudowie Star przedstawione na fotografii E, niezależnie od ich mocy maksymalnej, bez dodatkowego radiatora mogą rozproszyć do 1 W ciepła, czyli mogą pracować z prądem do 350 mA.
Można wykonać oddzielne, autonomiczne moduły iluminofonii na różne pasma częstotliwości i z diodami o różnych kolorach. Można też zrealizować wspólny przedwzmacniacz z jednym mikrofonem oraz pięć oddzielnych filtrów i układów wykonawczych z różnokolorowymi lampami. Czułość poszczególnych kanałów iluminofonii zapewne trzeba będzie dobrać indywidualnie (za pomocą R7), zależnie od warunków pracy i rodzaju muzyki.
Poznajemy elementy i układy elektroniczne
W wykładzie 10 mówiliśmy o „wspomaganiu”, gdy omawialiśmy filtry drugiego rzędu. Realizowaliśmy tam filtry w konfiguracji Sallena-Keya z wtórnikiem tranzystorowym.
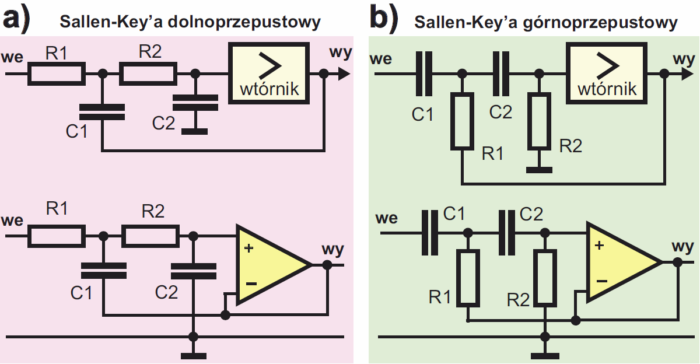
Filtry VCVS. Poznane wcześniej filtry o konfiguracji Sallena-Keya można z powodzeniem zrealizować na wzmacniaczu operacyjnym według rysunku 1.
Są one odmianą filtrów zwanych VCVS (Voltage Controlled Voltage Source), czyli ze źródłem napięciowym sterowanym napięciem. Tym źródłem sterowanym może być nie tylko wtórnik, ale też wzmacniacz nieodwracający – wtedy filtr będzie dodatkowo wzmacniał przepuszczane sygnały. Ogólny schemat filtru VCVS pokazany jest na rysunku 2a, a rysunki 2b, 2c i 2d przedstawiają filtry o różnych charakterystykach.
Filtry MFB. Filtr o danej charakterystyce można zrealizować na wiele sposobów. Prostą i popularną konfigurację mają filtry zwane MFB (Multiple FeedBack), czyli filtry wielopętlowe, filtry z wielokrotnym sprzężeniem zwrotnym. Ogólny schemat filtru MFB pokazany jest na rysunku 3a. Rysunki 3b, 3c, 3d pokazują filtry o różnych charakterystykach.
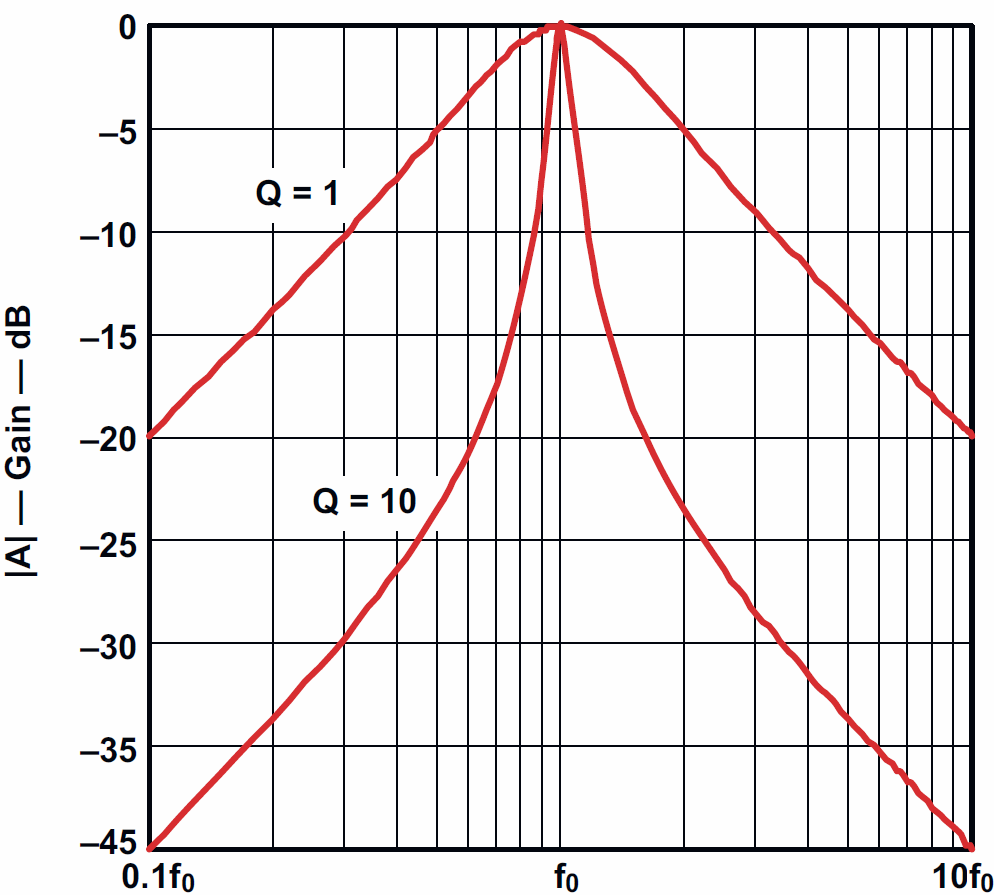
Zwróć uwagę, że filtry z rysunku 2d i 3d są filtrami środkowoprzepustowymi, które preferują tylko jedną częstotliwość – ich charakterystyka jest pojedynczą „górą”. Zależnie od wartości elementów, szczyt tej „góry” może być mniej lub bardziej stromy i wąski. Bardziej wąski i stromy jest w filtrach o dużej dobroci (oznaczanej literą Q) – rysunek 4.
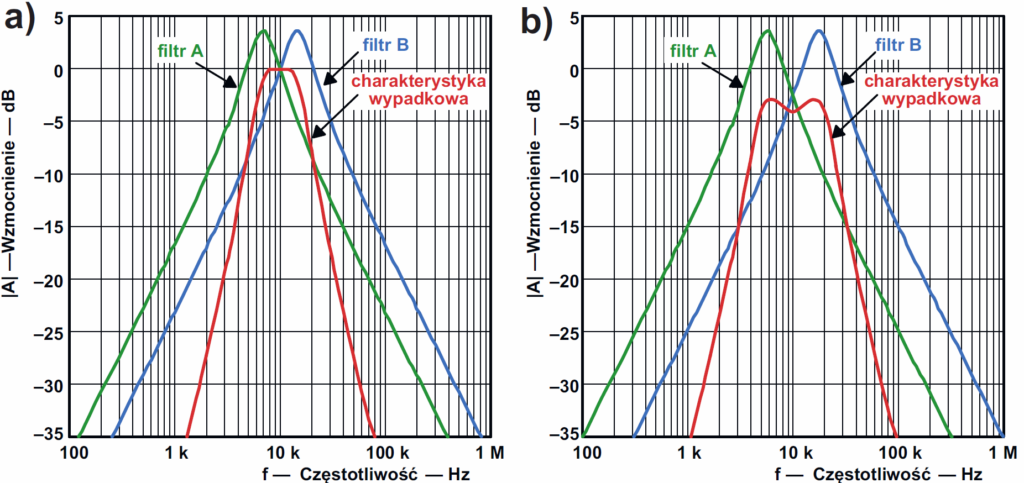
Początkujący na podstawie innych życiowych analogii często uważają, że czym większa dobroć Q, czyli czym węższa charakterystyka częstotliwościowa, tym lepiej. W rzeczywistości sytuacja wcale nie jest tak prosta. Duża dobroć oznacza jednocześnie dużą skłonność do „dzwonienia” po zaniku sygnału wejściowego, co w niektórych aplikacjach jest niedopuszczalne. Ponadto często bardzo wąskie pasmo nie jest wcale zaletą, bo potrzebne jest szersze pasmo przepustowe, ale jednocześnie wymagane są ostre, strome zbocza charakterystyki poza pasmem przenoszenia. Potrzebnej charakterystyki nie można uzyskać w pojedynczym filtrze, zmieniając jego dobroć. Trzeba zastosować dwa lub więcej filtrów o niedużej dobroci, by wspólnie wyznaczyły charakterystykę. W praktyce poszczególnych filtrów nie łączy się równolegle, tylko kaskadowo – jeden za drugim, czyli niejako w szereg, przy czym częstotliwości środkowe są odpowiednio rozsunięte. Łączenie kaskadowe polepsza stromości zboczy. Dla poszerzenia pasma rozsuwa się odpowiednio częstotliwości poszczególnych filtrów według rysunku 5a, ewentualnie jeszcze bardziej, jeżeli nie przeszkadza niewielkie „siodło” według rysunku 5b.
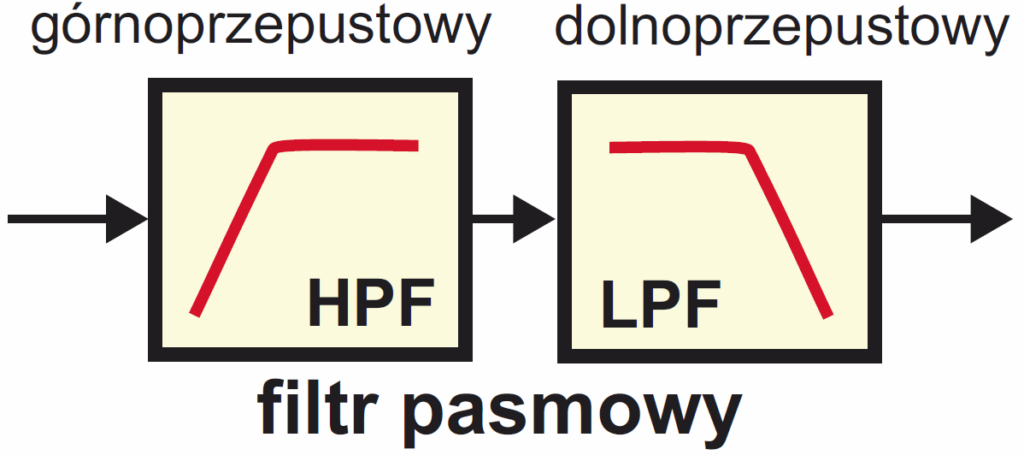
Przy odpowiedniej dobroci i rozsunięciu częstotliwości filtrów składowych można uzyskać szerokie, zupełnie płaskie pasmo, niejako „płaskowyż” o dużej szerokości. Jednak w takich przypadkach „szerokiego płaskowyżu” być może prościej będzie zastosować kaskadowe połączenie filtru dolno i górnoprzepustowego według rysunku 6.
Nie ma jednego jedynego, prostego wzoru na obliczenie wartości elementów filtrów o zadanych parametrach. Zarówno dla filtrów VCVS (Sallena-Keya), jak też MFB i innych, zależnie od wartości elementów, filtry o tej samej częstotliwości granicznej będą mieć odmienne właściwości, jeśli chodzi o przesunięcie fazy, tzw. opóźnienie grupowe oraz dobroć związaną ze wspomnianą wcześniej skłonnością do „dzwonienia”. W zależności od stosunku wartości elementów możemy otrzymać filtry o tej samej częstotliwości granicznej, ale o charakterystykach Bessela, Butterwortha, Czebyszewa oraz jeszcze innych (patrz wykład 10 rysunek 11).
Zrozumienie występujących tu zależności jest sprawą trudną. Zasadniczo projektowanie filtrów o określonych charakterystykach też nie jest zadaniem łatwym. Jednak w podręcznikach, a obecnie także w Internecie, można znaleźć różne recepty na projektowanie filtrów o pożądanych charakterystykach. Dostępne są też programy, które po wpisaniu potrzebnych parametrów podają gotowy schemat wraz z wartościami elementów. Przyjazny program tego rodzaju dostępny jest na stronie słynnej firmy Analog Devices: http://www.analog.com/designtools/en/filterwizard/#/type
Najpierw trzeba wybrać typ filtru (Low-Pass – dolnoprzepustowy, High-Pass – górnoprzepustowy lub Band-Pass – pasmowy), potem w zakładce Specifications określić kluczowe parametry, w tym częstotliwości charakterystyczne, wymaganą stromość zboczy i skłonność do „dzwonienia”. W zakładce Component selection można podać dalsze parametry, w tym wartości kluczowych elementów. Program momentalnie poda schemat z gotowymi wartościami elementów i licznymi charakterystykami.
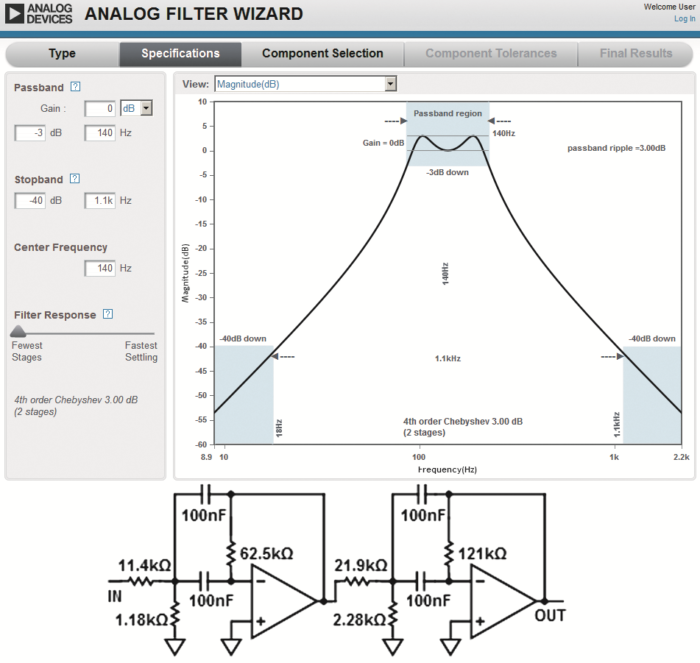
W naszej tytułowej iluminofonii wykorzystaliśmy dwustopniowy filtr z „siodłem”, projektowany właśnie w tym programie. Rysunek 7 pokazuje zrzut z ekranu przy zadawaniu parametrów filtru.
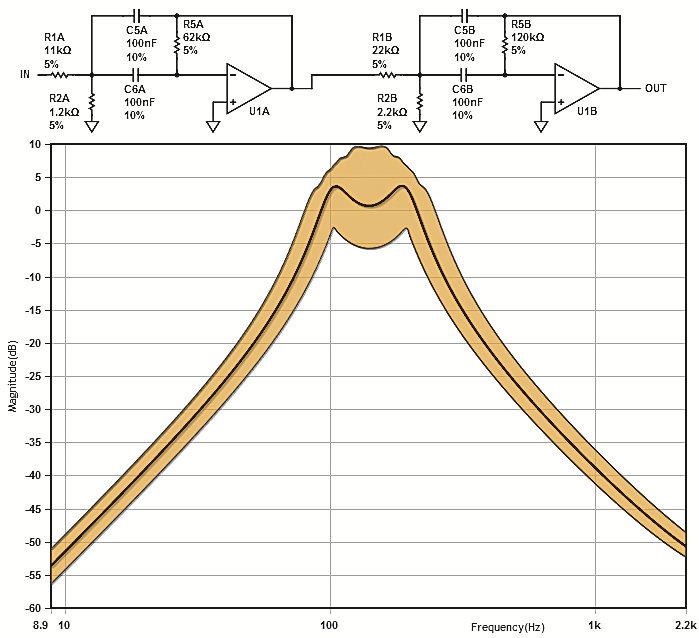
Chcieliśmy uzyskać filtr dwustopniowy o wzmocnieniu 1×(0dB), częstotliwości środkowej 140 Hz i paśmie też około 140 Hz. Dopuściliśmy „siodło” – maksymalną dla tego programu nierównomierność charakterystyki 3 dB. W dolnej części rysunku podane są idealne wartości elementów przy wykorzystaniu pojemności 100 nF. W dalszych krokach projektowania określiliśmy tolerancję kondensatorów 10 % i rezystorów 5 %, co dało układ i możliwe rozrzuty charakterystyki jak na rysunku 8. Ja w układzie tytułowym wykorzystałem nieco inną wersję takiego filtru, która dzięki innym stosunkom rezystorów przy okazji wzmacnia sygnał 10-krotnie, czyli o 20 dB.
Nasza powolna kostka LM358 słabo nadaje się do filtrów na wyższe częstotliwości, gdzie należy stosować szybkie wzmacniacze operacyjne, zwłaszcza w filtrach, które mają mieć dużą dobroć i jednocześnie wzmacniać sygnały użyteczne. Dlatego też nasz filtr pasmowy w układzie tytułowym pracuje w zakresie niższych częstotliwości (65 Hz…300 Hz). Przy wyższych częstotliwościach powolny LM358 nie spełniłby oczekiwań. Dlatego też w opisywanej procedurze podany jest odpowiednio szybki typ wzmacniacza operacyjnego z oferty Analog Devices.
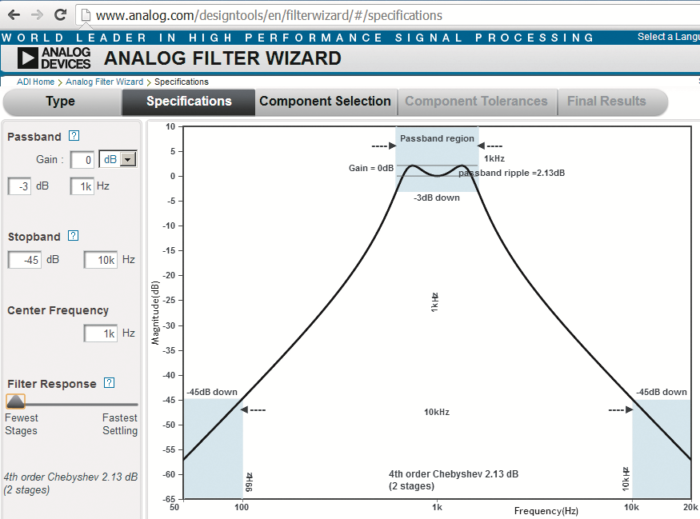
Rysunek 9 pokazuje realizację takiej procedury, gdy potrzebny jest filtr pasmowy o częstotliwości granicznej 1 kHz, paśmie przepustowym o szerokości 1 kHz (618 Hz…1,618 kHz), zapewniający tłumienie 45 dB dla częstotliwości 10 kHz (i 100 Hz).
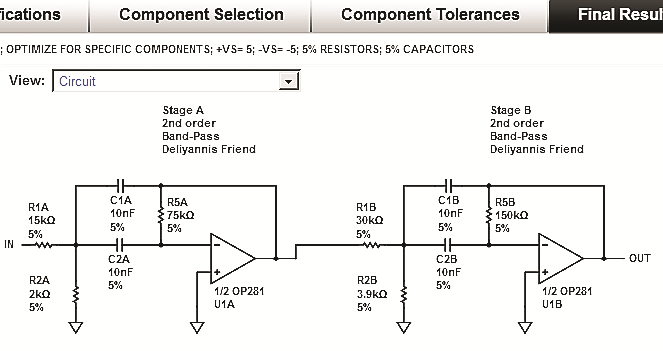
Jeśli dopuścimy nierównomierność charakterystyki w paśmie przepustowym 2 dB, to zadanie to zrealizuje filtr dwustopniowy według rysunku 10. Gdyby pasmo miałoby być mniej pofalowane, potrzebny będzie filtr trzystopniowy.
Za pomocą tego typu programów można samodzielnie projektować filtry o pożądanych charakterystykach. Uzyskanie odpowiedniej charakterystyki częstotliwościowej jest łatwe, ale w niektórych zastosowaniach duże znaczenie mają też charakterystyki fazowe oraz kwestia tzw. opóźnienia grupowego. Wtedy wymagane jest więcej wiedzy.
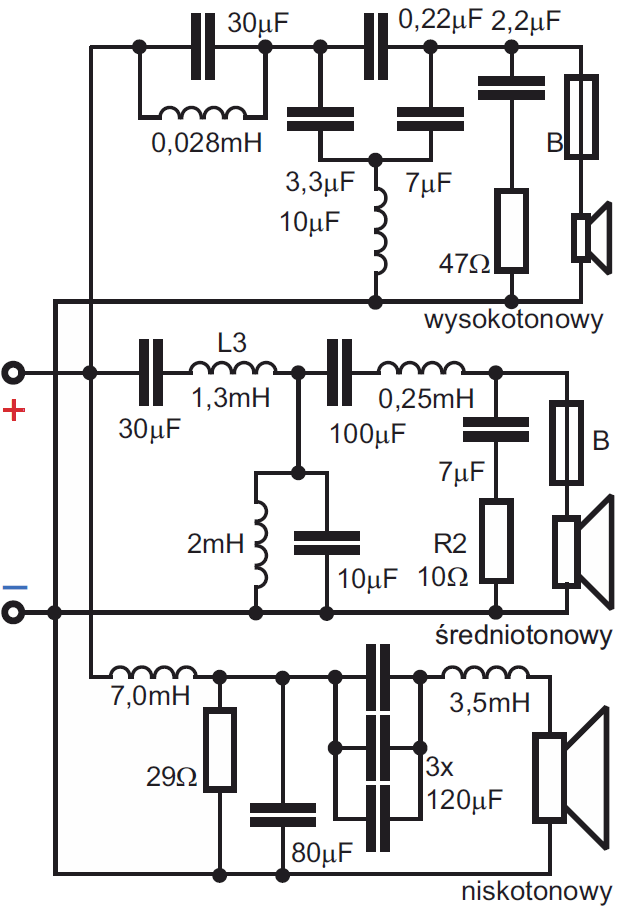
Znacznie więcej wiedzy wymaga też na przykład projektowanie zwrotnic do kolumn głośnikowych. Klasyczna zwrotnica to zestaw filtrów LC współpracujących z głośnikami: nisko-, średnio- i wysokotonowym. W najprostszym przypadku w kolumnach zawierających dwa głośniki, funkcję prymitywnej zwrotnicy pełni kondensator o pojemności kilku mikrofaradów. W lepszej klasy kolumnach zwrotnica jest rozbudowana, zawiera trzy filtry dla trzech głośników, a czasem też tzw. obwody Zobela (Zobel network) korygujące reaktancję. Takie klasyczne zwrotnice budowane są z użyciem foliowych kondensatorów (C) i dużych cewek (L), a czasem też rezystorów – rysunek 11.
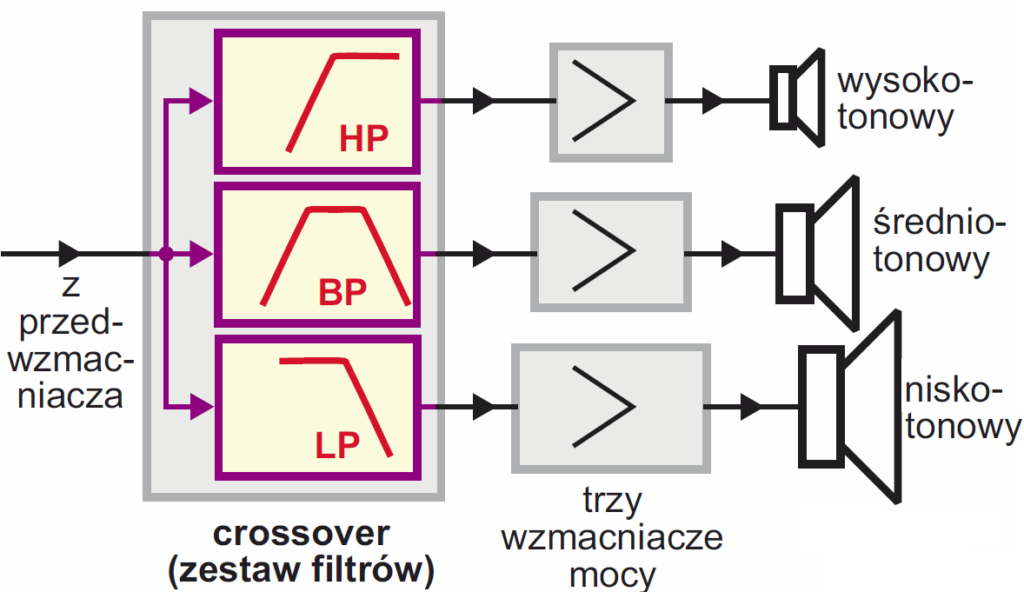
Dziś coraz częściej zamiast klasycznych zwrotnic LC wbudowanych w kolumnę stosuje się tak zwane aktywne crossovery, czyli różnej konstrukcji filtry aktywne, zbudowane w oparciu na wzmacniaczach operacyjnych, a głośniki zasilane są przez oddzielne wzmacniacze – rysunek 12.
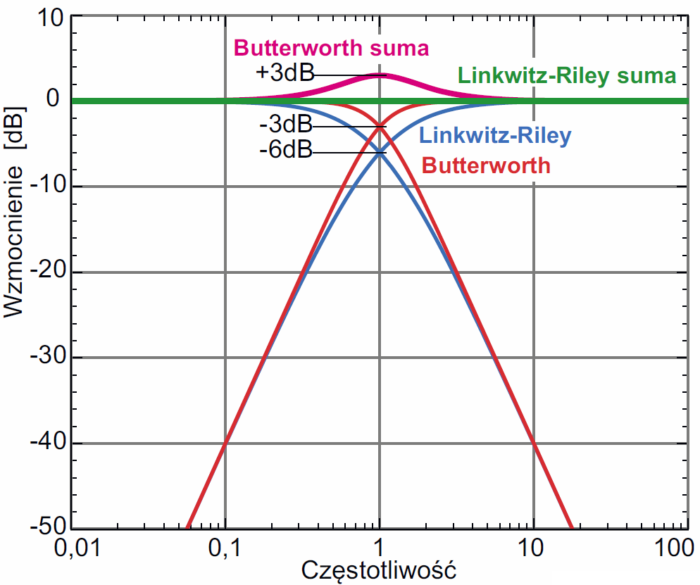
I właśnie budowa dobrych filtrów aktywnych – crossoverów, wymaga dużej wiedzy i doświadczenia. Zwykle wykorzystywane są tam tzw. filtry Rileya-Linkwitza, których wersje o większych stromościach są odmianą filtrów Butterwortha, mającą na celu m.in. usunięcie niewielkiego podbicia sumarycznej charakterystyki w pobliżu częstotliwości podziału, co ilustruje rysunek 13.
Gotowe przykłady crossoverów o mniej i bardziej stromych zboczach charakterystyki można znaleźć w Internecie – wystarczy w grafice poszukać: crossover schematic. W najlepszych instalacjach celem jest nie tylko uzyskanie płaskiego pasma wypadkowego na granicy pasm poszczególnych filtrów. W grę wchodzą też zależności fazowe i opóźnienia, wynikające choćby z umieszczenia głośników w znacznej odległości (kilkadziesiąt cm) od siebie. Są to bardzo obszerne, trudne zagadnienia, związane z subtelnymi właściwościami kolumn, propagacji dźwięku i specyfiki ludzkiego słuchu. I właśnie między innymi w crossoverach wykorzystywane są tak zwane filtry wszechprzepustowe, których charakterystyka amplitudowa jest zupełnie płaska, wywołując zdziwienie i niedowierzanie początkujących elektroników.
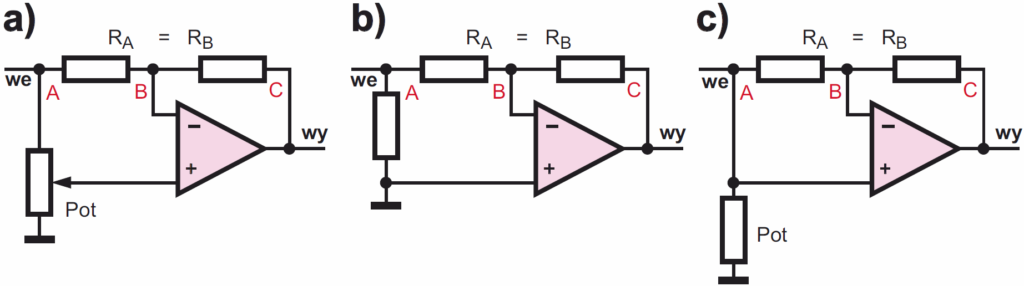
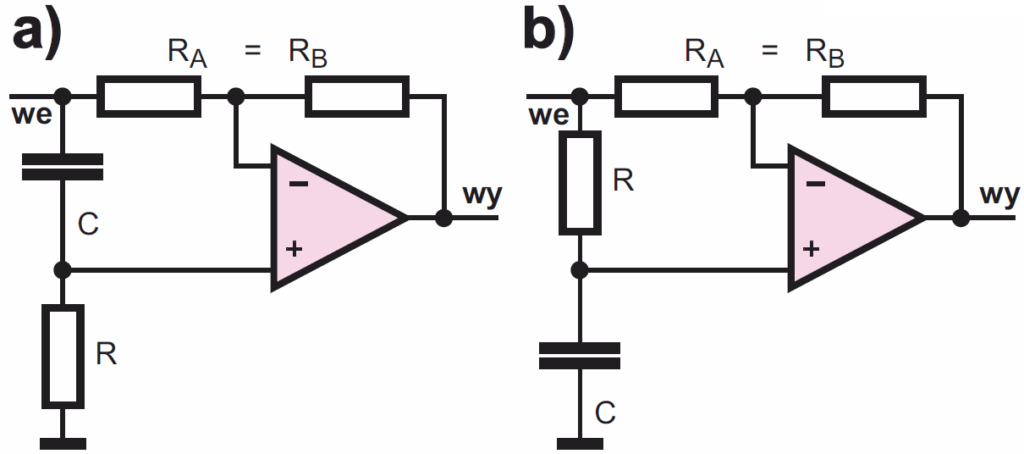
Aby to wyjaśnić, przeanalizujmy najpierw prosty układ z rysunku 14a z dwoma jednakowymi rezystorami RA, RB. Potencjometr P pozwala płynnie zmieniać wzmocnienie w zakresie –1…0…+1. W dolnym skrajnym położeniu (rysunek 14b) mamy zwyczajny wzmacniacz odwracający o wzmocnieniu –1. Podkreślmy, że „odwrócenie sygnału” to inaczej mówiąc przesunięcie fazy o pół okresu, czyli o 180 stopni. W górnym skrajnym położeniu suwaka potencjometru mamy nieco dziwny układ jak na rysunku 14c, gdzie sygnał wejściowy podawany jest bezpośrednio na wejście nieodwracające. Zasada działania wzmacniacza operacyjnego mówi, że podczas normalnej pracy wzmacniacz dąży do wyrównania napięć na obu wejściach. Aby napięcie na wejściu odwracającym było takie samo, jak na nieodwracającym, spadek napięcia na RA musi być równy zeru. A to oznacza, że przez RA i RB nie może płynąć prąd i napięcia w punktach A, B, C muszą być równe. Aby tak było, na wyjściu wzmacniacza musi wystąpić taki sam przebieg, jak na wejściu, czyli układ będzie wtórnikiem o wzmocnieniu +1.
Co ciekawe, jeżeli zastąpimy potencjometr obwodem RC, według rysunku 15a, otrzymamy tak zwany przesuwnik fazy, inaczej mówiąc filtr wszechprzepustowy (all-pass filters), którego wzmocnienie w całym paśmie jest stałe, równe jedności, czyli 0 dB, natomiast przesunięcie fazy jest zależne od częstotliwości. Przy bardzo małych częstotliwościach kondensator C1 ma ogromną reaktancję i praktycznie jest rozwarciem, przerwą, więc sytuacja wygląda jak na rysunku 14b – przesunięcie fazy wynosi 180 stopni a wzmocnienie jest równe jedności. Przy bardzo dużych częstotliwościach reaktancja kondensatora jest bliska zeru (zwarcie), więc sytuacja jest jak na rysunku 14c – wzmocnienie jest równe jedności, a przesunięcie fazy bliskie zeru. Dla częstotliwości charakterystycznej f = 1/2πRC wzmocnienie też wynosi jeden, a przesunięcie fazy to dokładnie 90 stopni. Zmieniając wartość stałej czasowej obwodu RC, zmienimy częstotliwość charakterystyczną takiego przesuwnika. Zdecydowanie mniej popularna jest wersja przesuwnika z rysunku 15b, która pełni praktycznie takie same funkcje, tylko przesuwanie fazy jest w niej w pewnym sensie „odwrotne”.
Początkujący zastanawiają się, po co komu takie „bezsensowne filtry”, które nie filtrują…
Otóż właśnie takie dziwne filtry wszechprzepustowe znajdują zastosowanie między innymi przy budowie crossoverów, czyli aktywnych zwrotnic przeznaczonych do kolumn głośnikowych wysokiej jakości. Służą tam do korekcji fazy i opóźnienia.
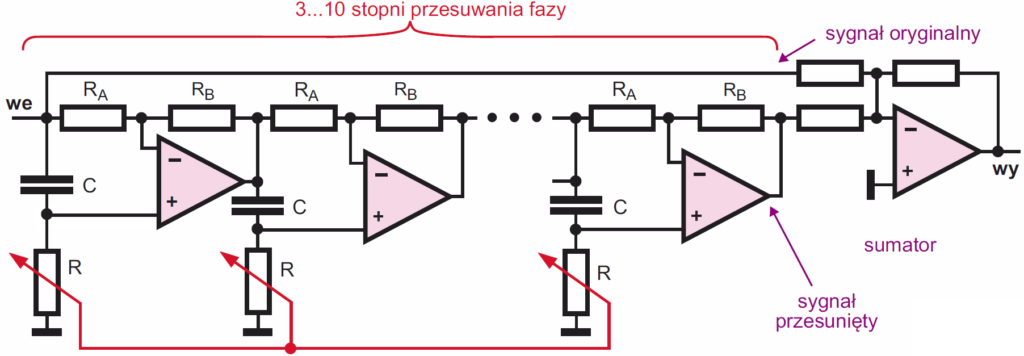
Innym bardzo interesującym przykładem zastosowania przesuwników fazy jest efekt gitarowy znany jako fazer (phaser). Po pierwsze w fazerze występuje wiele ogniw przesuwnika fazy – czym więcej, tym lepszy efekt, po drugie, częstotliwości charakterystyczne ogniw przesuwnika nie są stałe, tylko można je zmieniać i po trzecie na wyjściu fazera występuje sygnał będący sumą przebiegu „przesuniętego” i oryginalnego, przez co sygnały o poszczególnych częstotliwościach dodają się i odejmują, zależnie właśnie od fazy, dając efekt tzw. grzebienia o „liczbie zębów” zależnej od liczby ogniw przesuwnika fazowego. Uproszczona idea fazera gitarowego pokazana jest na rysunku 16, przy czym zamiast zespołu sprzężonych potencjometrów, stosowane są zmienne rezystancje, sterowane zazwyczaj generatorem przebiegu trójkątnego.
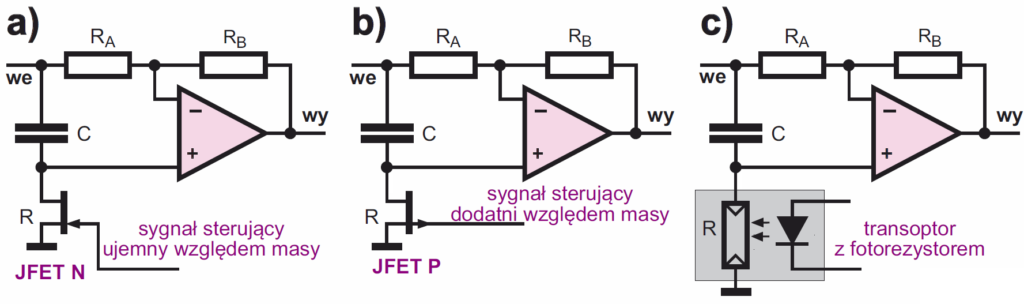
Tymi zmiennymi rezystancjami są tranzystory polowe JFET albo fotorezystory współpracujące z diodą LED lub żaróweczką według rysunku 17. W Internecie można znaleźć mnóstwo schematów fazerów – wystarczy wpisać w wyszukiwarkę: phaser schematic.
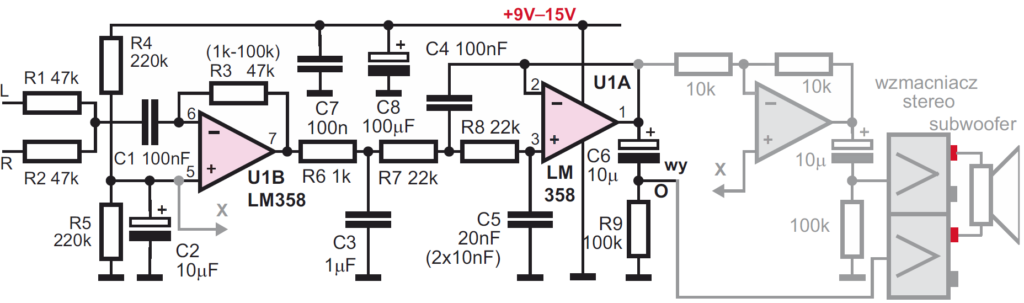
Zrealizujmy natomiast filtr do subwoofera, czyli jak największego głośnika przeznaczonego do odtwarzania tylko najniższych tonów. Rysunek 18 pokazuje schemat, a fotografia 19 – model.
Przy idealnych wartościach elementów częstotliwość graniczna (przy spadku o 3 dB) wynosi 167 Hz. Do wejść L, R doprowadzamy dowolny sygnał stereo. Układ U1B pracuje jako sumator i dodaje sygnały z obu kanałów. Następnie filtr trzeciego rzędu na układzie U1A tłumi i obcina sygnały o częstotliwościach powyżej 167 Hz. Sygnał wyjściowy z punktu O doprowadzony jest do wzmacniacza mocy subwoofera. Szarym kolorem zaznaczona jest dodatkowa część potrzebna wtedy, gdy chciałbyś do sterowania głośnika subwoofera wykorzystać wzmacniacz dwukanałowy, dowolny wzmacniacz stereo, pracujący w połączeniu mostkowym BTL (Bridge Tied Load). Wtedy dwa wzmacniacze sterowane są sygnałami o przeciwnej fazie, napięcie na głośniku jest dwa razy większe, a moc teoretycznie może być 4 razy większa.
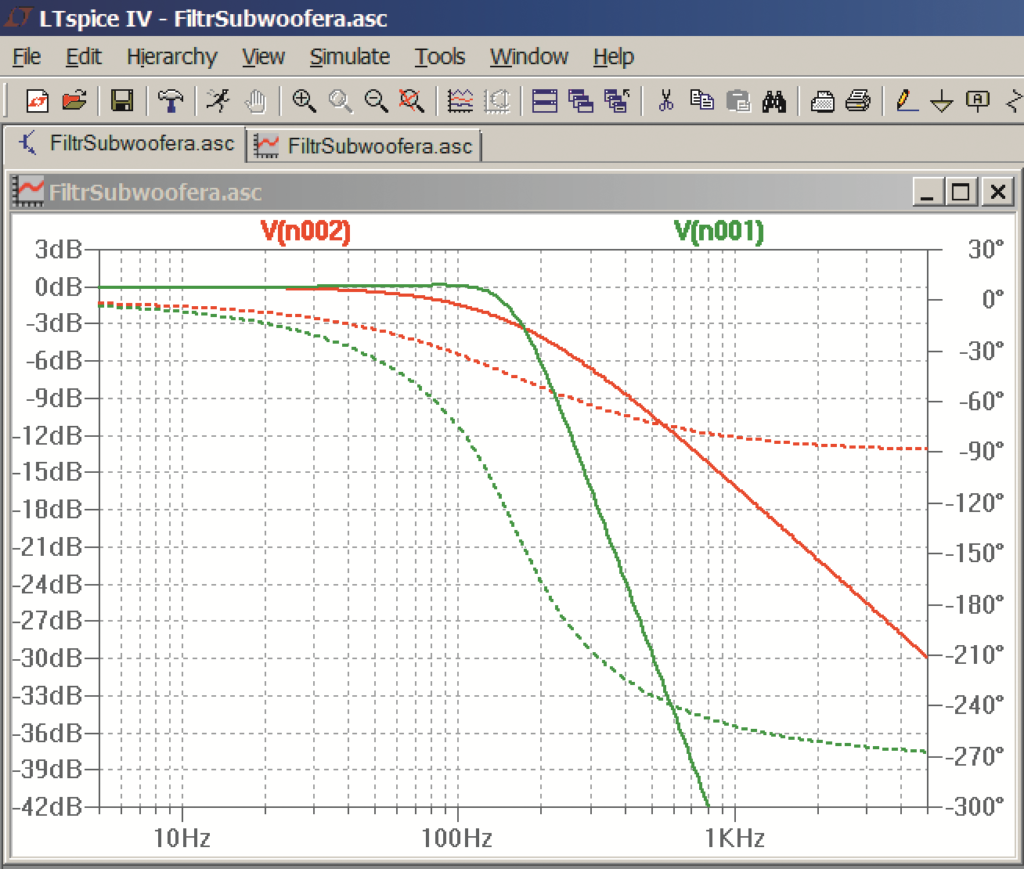
Rysunek 20 pokazuje charakterystykę naszego filtru subwoofera – to krzywe zielone. Dla porównania krzywe czerwone pokazują charakterystykę pojedynczego obwodu RC, czyli filtru pierwszego rzędu. Linie ciągłe to charakterystyka amplitudowa, a linie przerywane – fazowa.
Możesz łatwo zwiększyć częstotliwość graniczna filtru, proporcjonalnie zmniejszając wartości kondensatorów C3, C4, C5. Na przykład przy wartościach C3 = 680 nF, C4=68 nF, C5 = 15 nF częstotliwość graniczna wyniesie około 230 Hz.
Rysunek 20 pochodzi z kolejnego bardzo interesującego i pożytecznego programu LTspiceIV udostępnionego bezpłatnie przez znaną firmę Linear Technology (www.linear.com/designtools/software). Ten program z rodziny SPICE to program do dokładnej symulacji układów elektronicznych. Wystarczy narysować schemat, określić wartości elementów i ich właściwości, a potem dokonać symulacji. Programy tego typu mają ogromne możliwości i oprócz charakterystyk, jak na rysunku 20, można przez symulację określić wiele innych właściwości danego układu.
Moglibyśmy też na wzmacniaczu operacyjnym zrealizować tzw. filtr kroków, który w torze mikrofonowym obcina sygnały o najniższych częstotliwościach, poniżej 100 Hz, których nie ma w głosie człowieka, a które czasem mocno przeszkadzają, jak właśnie odgłos kroków na estradzie czy porywy wiatru. Jednak nasz wzmacniacz LM358 jest powolny i niebyt dobrze nadaje się do takich zastosowań.
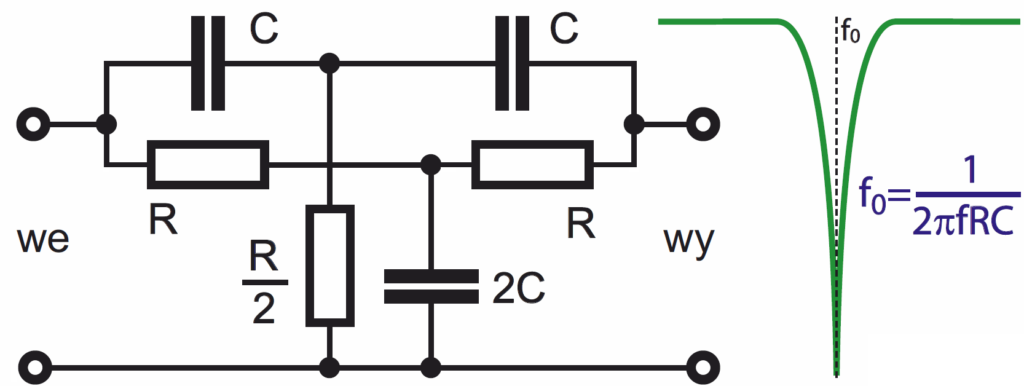
Wspomnijmy jeszcze, że oprócz filtrów dolno-, górno- i pasmowoprzepustowych, dość często wykorzystywane są filtry zaporowe, zwykle nazywane notch filters. Najczęściej ich zadaniem jest usunięcie jednej określonej częstotliwości. Popularny podręcznikowy schemat filtru zwanego podwójne T (TT) z rysunku 21 okazuje się praktycznie bezużyteczny, ponieważ ma małą dobroć, a jego dostrojenie do pożądanej częstotliwości jest bardzo kłopotliwe.
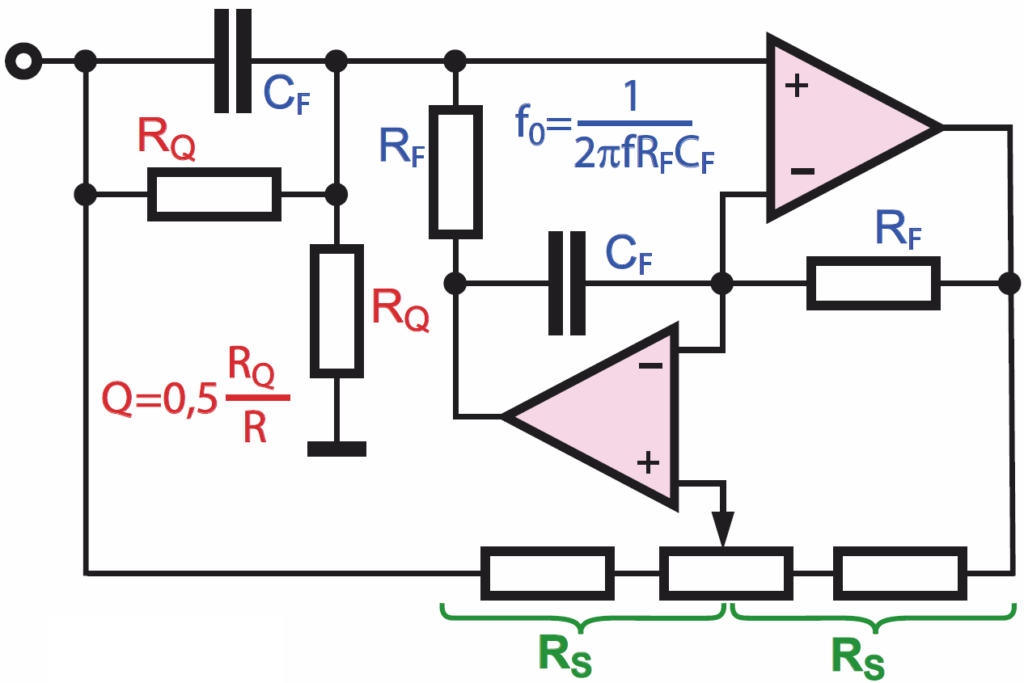
Opracowano mnóstwo filtrów zaporowych o lepszych parametrach, w których strojenie częstotliwości i dobroci jest niezależne. Przykładem może być pokazany na rysunku 22 filtr Fliege’a, którego układ i zasady działania trudno wytłumaczyć intuicyjnie. Pary (w miarę) jednakowych rezystorów RF i kondensatorów CF wyznaczają częstotliwość zaporową. Jednakowe rezystory RQ określają dobroć.
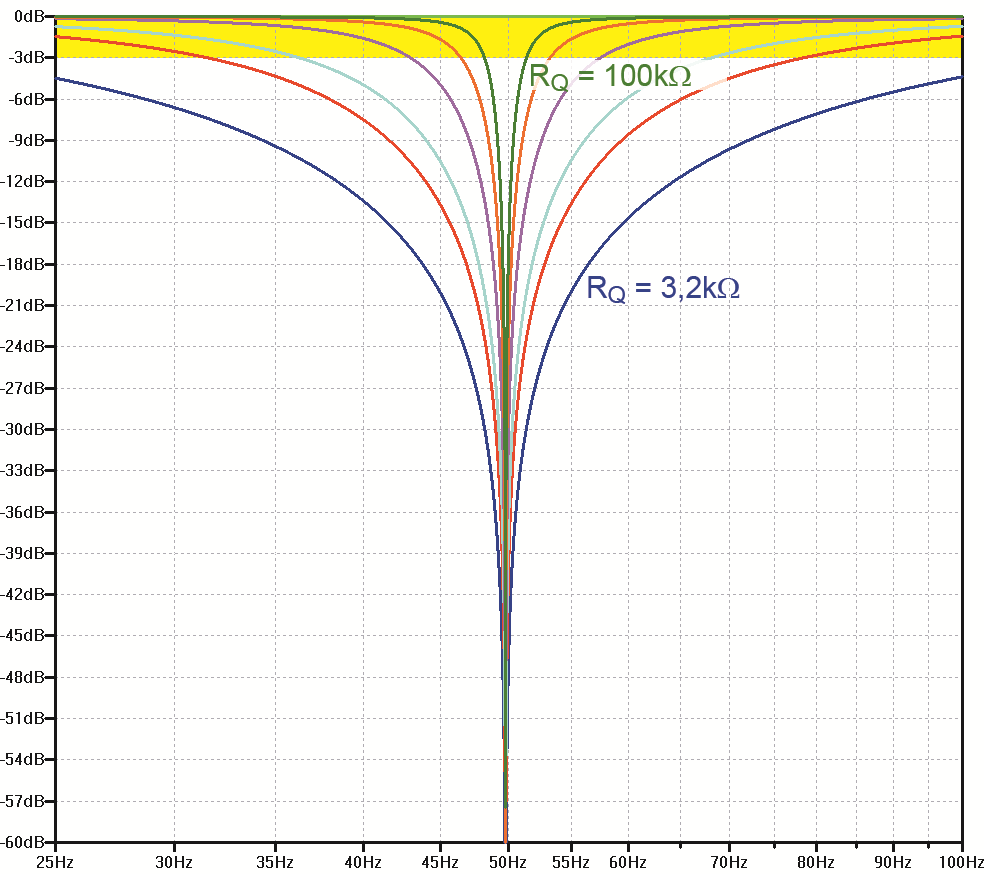
Rysunek 23 pokazuje wpływ rezystancji RQ w przykładowym filtrze o częstotliwości zaporowej 50 Hz (RF =3,2 kΩ, CF =1 uF, RS = 52 kΩ). W praktyce elementy RF, CF, RQ mogą mieć tolerancję 5…10%, trzeba tylko skorygować wartości któregoś z elementów RF, żeby dostroić się do potrzebnej częstotliwości. Także jednakowe rezystancje RS trzeba dobrać jak najdokładniej, stąd obecność potencjometru.
W literaturze i w Internecie można znaleźć liczne sposoby realizacji najróżniejszych filtrów.
W następnym wykładzie poznamy kolejne interesujące zastosowania wzmacniaczy operacyjnych.
Piotr Górecki