PKE – Praktyczny Kurs Elektroniki (22) Elektroniczna świeczka
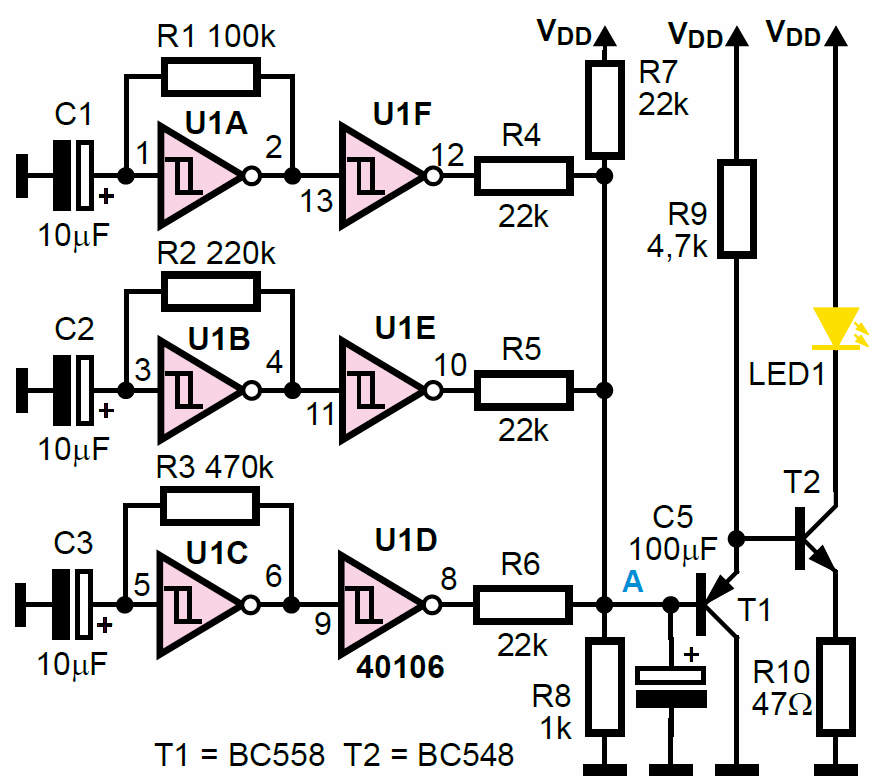
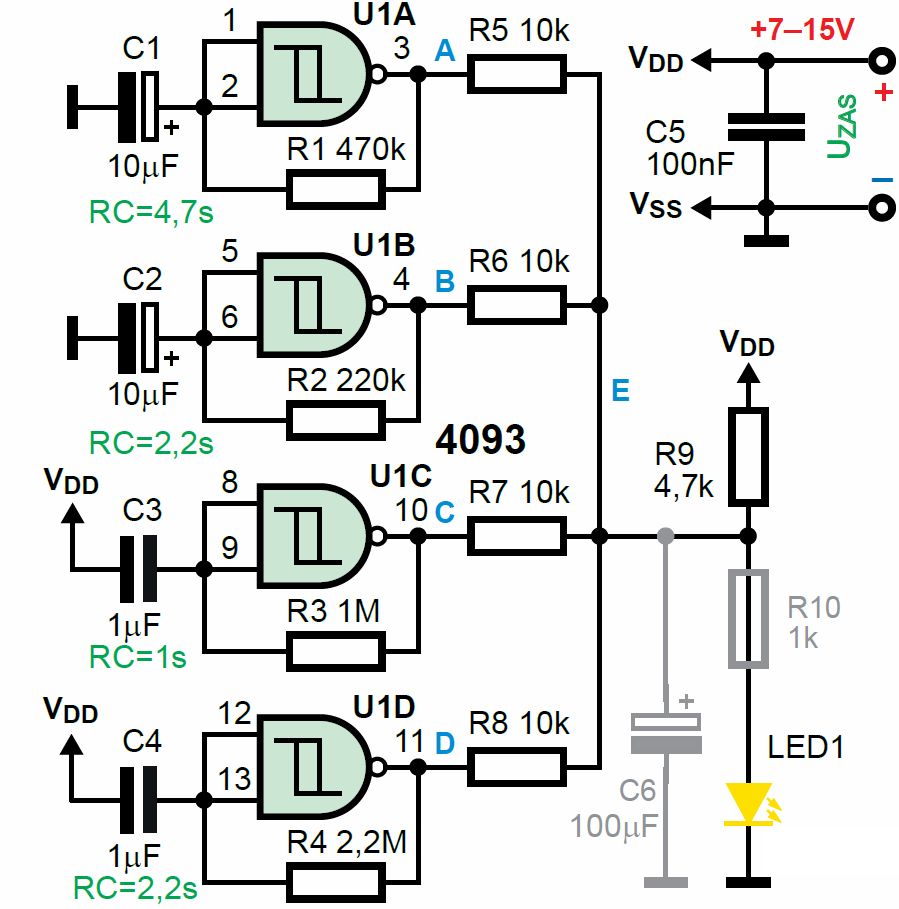
Fotografia tytułowa pokazuje dwa modele elektronicznej świeczki. W obu pracuje żółta dioda LED, która naśladuje płomień klasycznej świeczki: w nieregularnym rytmie przygasa i rozświetla się. Schematy dwóch wersji elektronicznej świeczki pokazane są na rysunku A oraz rysunku B. Pierwsza, prostsza, przeznaczona jest do zasilania napięciem 7…15 V, druga może też prawidłowo pracować przy znacznie niższych napięciach, zależnie od wartości rezystora R10.
Dwa poniższe schematy udowadniają, że za pomocą garstki elementów można zrealizować układ elektroniczny dający efekt podobny do płomienia prawdziwej świecy.
Opis układu dla „zaawansowanych”
W wersji prostszej z rysunku A i z lewej strony fotografii tytułowej, dioda LED1 sterowana jest bezpośrednio sumą sygnałów prostokątnych z punktów A, B, C, D. Te sygnały prostokątne są wytwarzane przez cztery niezależne generatory na czterech bramkach kostki U1. Kondensatory C3, C4 zostały dołączone do plusa zasilania tylko po to, by uprościć montaż modelu. Równie dobrze mogłyby być dołączone do masy.
Wprawdzie nominalne stałe czasowe R2C2 oraz R4C4 są jednakowe – 2,2 sekundy, jednak z uwagi na rozrzut (tolerancję) elementów, najprawdopodobniej także te dwa generatory nie będą ze sobą zsynchronizowane.
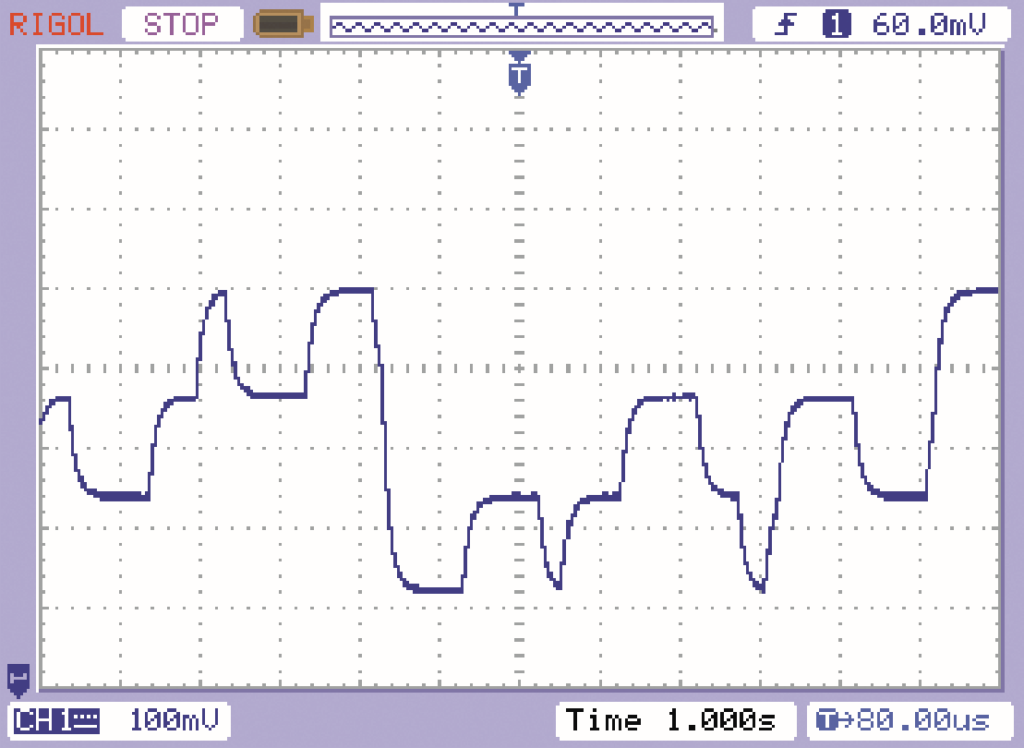
Wszystkie generatory pracują z małymi częstotliwościami, rzędu 1 Hz i mniej. Jednak z uwagi na to, że nie są one zsynchronizowane, w wypadkowym przebiegu zmiany mogą występować i występują dużo częściej, niż co sekundę. Rysunek C pokazuje przebieg w punkcie E (skala czasu wynosi 1 s/działkę), gdy odłączone są rezystor R9 i dioda LED1.
Rezystor R9 powoduje, że dioda rzadziej zmniejsza swą jasność do zera, co bardziej realistycznie symuluje płomień świecy. W wersji podstawowej, bez elementów C6, R10 dioda LED1 zasilana jest przebiegiem „schodkowym”. Można dodać kondensator C6 o pojemności 100 uF i rezystor R10 = 1 kΩ, co „złagodzi schodki”. Na rysunku D pokazane są w powiększeniu (10 mV/dz) przebiegi na diodzie LED bez C6 i R10 oraz z C6 = 100 uF, R10 = 1 kΩ.
W układzie tym możesz śmiało zmieniać wartości elementów C1…C4 i rezystorów R1…R4. Zachęcam do eksperymentów i zmiany. Najlepszą symulację świeczki uzyskuje się wtedy, gdy stałe czasowe RC generatorów wynoszą 1…5 sekund, ale Ty z powodzeniem możesz wypróbować inne wartości.
W układzie z rysunku A możesz też zmieniać wartości rezystorów R5…R8 z zakresie 2,2 kΩ … 22 kΩ, przy czym nie muszą być one równe.
Gdybyś chciał praktycznie wykorzystać taką elektroniczną świeczkę i gdyby miała ona świecić jak najdłużej, należałoby ją zasilać nie z baterii 9V, tylko z trzech ogniw AA (R6), czyli napięciem około 4,5 V albo z trzech akumulatorków NiMH napięciem 3,6 V lub z jednego akumulatora litowego (3,7 V). Przy takich niskich napięciach zasilania wydajność prądowa wyjść układów CMOS jest mała i trudno z nich wysterować bezpośrednio diody LED. Problem w tym, że przy niskim napięciu zasilania trzeba zmniejszać wartość szeregowych rezystorów, tymczasem przy niskim napięciu zasilania rośnie rezystancja wyjściowa bramek.
Pojawia się ryzyko, że nadmiernie obciążona bramka przestanie pracować jako generator. Aby pozbyć się problemu i zmniejszyć straty w rezystorach „sumujących”, zrealizowaliśmy według rysunku B drugą wersję świeczki, która będzie prawidłowo pracować także przy niskich napięciach zasilania. Tutaj podobnie sumujemy sygnały z wyjść generatorów za pomocą rezystorów R4, R5, R6. Rezystor R7 zapobiega całkowitemu wygaszaniu diody LED. Z kolei rezystor R8 o niewielkiej wartości 1 kΩ powoduje, że w punkcie A przebieg zmienny ma niewielką wartość. Rysunek E pokazuje przebieg w punkcie A przy zasilaniu układu napięciem 4,0 V. Napięcie z rezystora R8 doprowadzone jest do bazy T1 czyli do wejścia sterowanego źródła prądowego z tranzystorami T1, T2. Mój model, pokazany z prawej strony fotografii tytułowej, zaczynał pracę (lekkie świecenie diody LED1) już przy napięciu zasilania 2,1 V.
Poznajemy elementy i układy elektroniczne
W poprzednim wykładzie poznaliśmy przerzutniki synchroniczne D, T oraz JK. Przerzutniki te pozwalają realizować kolejne nad wyraz pożyteczne układy.
Rejestry
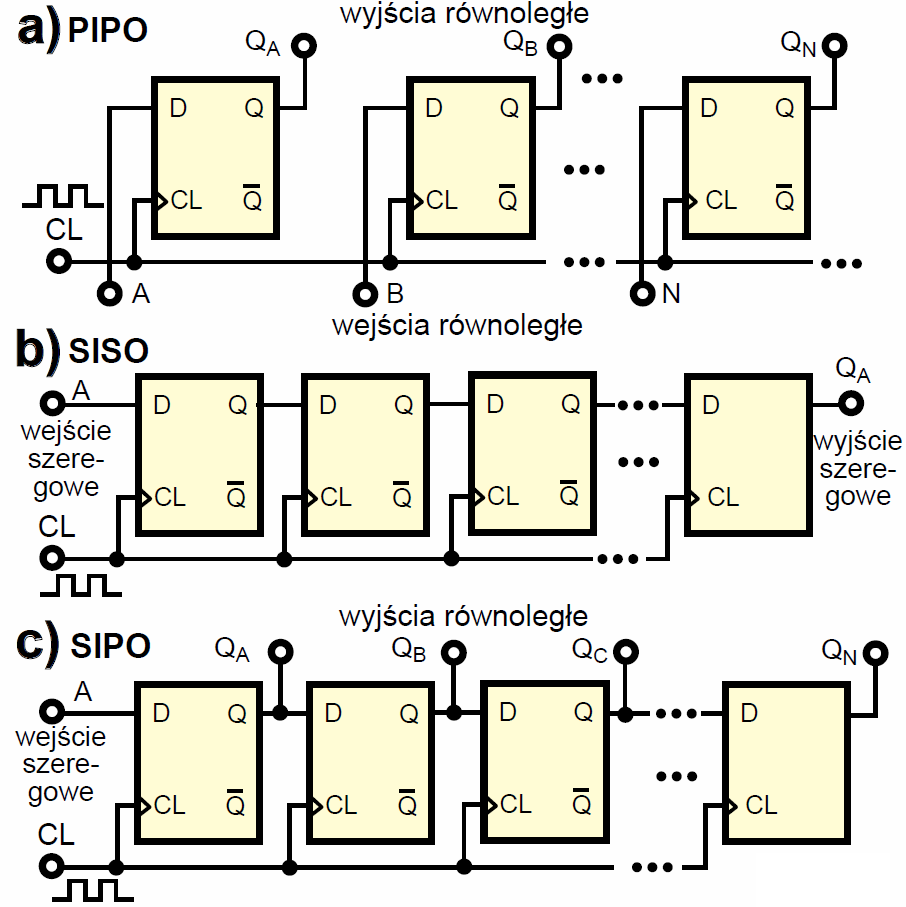
Przerzutnik D jest bodaj najprostszą pamięcią: aktywne zbocze powoduje zapamiętanie w przerzutniku stanu wejścia D. Łącząc kilka przerzutników D, by miały wspólny sygnał zegarowy, można uzyskać tak zwane rejestry. Rysunek 1a pokazuje rejestr „równoległy” (zwany PIPO – Parallel Input Parallel Output), który zapamiętuje na wyjściach stany wejść, występujące tam w chwili wystąpienia aktywnego zbocza impulsu zegarowego. Jest to swego rodzaju bufor pamiętający. W praktyce najpopularniejsze okazują się rejestry z ośmioma przerzutnikami, czyli tak zwane ośmiobitowe.
Rysunek 1b pokazuje rejestr szeregowy (zwany SISO – Serial Input Serial Output) z jednym wejściem i jednym wyjściem. Na pierwszy rzut oka mogłoby wyglądać, że zawartość wejścia A natychmiast „przeleci” przez cały rejestr. Tak byłoby z omawianymi wcześniej przerzutnikami D-latch, które są „przezroczyste”, gdy na wejściu zegarowym jest poziom aktywny (wysoki). Natomiast „prawdziwy” przerzutnik D jest wyzwalany zboczem i stan jego wyjść może zmienić się tylko pod wpływem i tylko w chwili występowania aktywnego zbocza, a ponadto w układach logicznych między wejściem a wyjściem zawsze występują niewielkie opóźnienia (rzędu nanosekund). I właśnie te opóźnienia oraz fakt, że przerzutnik D reaguje tylko na zbocze powodują, że w rejestrze SISO zawartość wejścia nie „przeleci” przez całą długość rejestru. Każde aktywne zbocze sygnału zegarowego niejako przesuwa zawartość rejestru „w prawo” tylko o jeden stopień, przy czym do pierwszego przerzutnika wpisywana jest zawartość wejścia A, a zawartość ostatniego przerzutnika jest tracona.
Przykład takiego rejestru szeregowego podkreśla też konieczność stosowania sygnału zegarowego o ostrych zboczach. W realnych układach występują pewne rozrzuty parametrów poszczególnych przerzutników, między innymi progów przełączania. Gdyby więc wspólny sygnał zegarowy miał łagodne zbocza, reakcje poszczególnych przerzutników mogłyby nastąpić nie w jednej chwili, tylko z pewnym opóźnieniem, co spowodowałoby błędną, nieprzewidywalną pracę rejestru. Dlatego w katalogach podany jest maksymalny czas narastania aktywnego zbocza sygnału zegarowego.
Omawiany rejestr SISO jest rodzajem pamięci szeregowej i cyfrowym układem opóźniającym. Wersja z rysunku 1c to prosty rejestr zwany SIPO z pojedynczym wejściem i wieloma wyjściami. Pozwala on w takt zegara zapamiętywać stan wejścia A, przy czym wcześniejsze stany są przesuwane w prawo i pojawiają się na kolejnych wyjściach.
Idąc krok dalej, moglibyśmy analogicznie narysować schemat rejestru PISO z równoległymi wejściami i pojedynczym wyjściem. Tylko taki rejestr byłby mało użyteczny. Aby był użyteczny, powinien to być rodzaj rejestru szeregowego, do którego wstępnie jednorazowo można byłoby wpisać stan wejść równoległych, a w takt zegara przesunąć zawartość w prawo do wyjścia. Takie wstępne wpisywanie można zrealizować na różne sposoby. Można byłoby wykorzystać rejestr SISO i wstępnie wpisywać zawartość wejść równoległych asynchronicznie, czyli niezależnie od sygnału zegarowego, wykorzystując asynchroniczne wejścia Set i Reset jakie istnieją w wielu przerzutnikach. Prosty przykład masz na rysunku 2a. Krótki impuls na wejściu Load powoduje załadowanie do (wcześniej wyzerowanych) przerzutników stanów z równoległych wejść A, B, C,… Następnie impulsy zegarowe CL powodują przesuwanie zawartości w prawo i na wyjściu Q kolejno pojawiają się stany wejść.
Ładowanie zawartości wejść może się też odbywać synchronicznie. Rysunek 2b pokazuje przykład takiego rozwiązania. Gdy na wejściu Ctrl panuje stan niski, wtedy każde aktywne zbocze sygnału zegarowego synchronicznie wpisuje stany wejść A, B, C,… do przerzutników. Gdy na wejściu Ctrl panuje stan wysoki, każdy impuls zegarowy powoduje przesunięcie zawartości rejestru w prawo, do wyjścia (a do pierwszego przerzutnika wpisywany jest stan wejścia A co nie ma istotnego znaczenia).
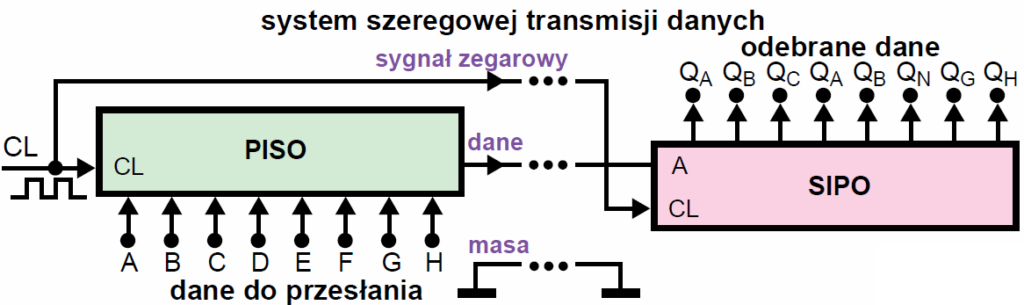
Rejestry PISO i SIPO często współpracują ze sobą przy tak zwanym szeregowym przesyłaniu danych. Mocno uproszczony rysunek 3 pokazuje ideę systemu transmisji szeregowej, gdzie za pomocą trzech przewodów można przesyłać dane w takt impulsów zegarowych. Na rysunku 3 pokazana jest tylko podstawowa idea. Szeregowe przesyłanie danych jest ogromnie popularne (tak pracują popularne łącza szeregowe łącze USB, RS-232 i inne), a w praktyce wykorzystuje się dodatkowo różne sprytne pomysły, a obwody nadawczo-odbiorcze są znacznie bardziej rozbudowane.
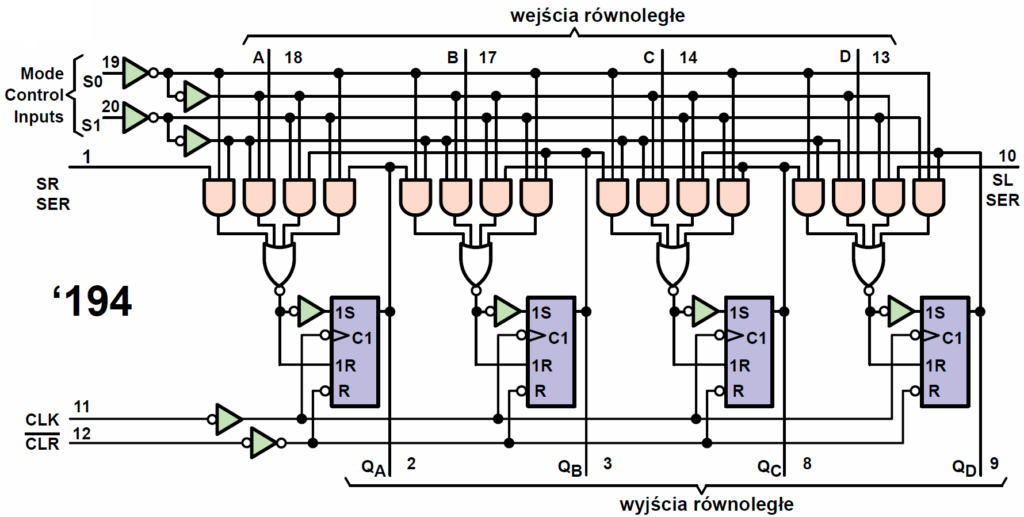
Przerzutniki tworzące rejestry (które nie muszą być typu D-flipflop) można wzbogacić w obwody pomocnicze, pozwalające zerować i ustawiać stan przerzutników. Przez dodanie do każdego przerzutnika kilku bramek i wejścia sterującego kierunkiem, można zrealizować rejestry, przesuwające zawartość w obie strony. Niektóre rejestry mają dodatkowe bufory w postaci przerzutników D-latch, niektóre mają wyjścia trójstanowe (tristate outputs) i dodatkowe wejście sterujące OE (Output Enable). Rysunek 4 pokazuje schemat wewnętrzny 4-bitowego dwukierunkowego rejestru uniwersalnego, odpowiednika kostki 74194 (40194), a rysunek 5 – uniwersalnego 8-bitowego rejestru 74LS299.
Zasadniczo wszystkie rejestry są swego rodzaju pamięciami. Warto wspomnieć, że mając zestaw rejestrów dwukierunkowych można zbudować tak zwany stos, który jest specyficznym rodzajem niewielkiej pamięci, stosowanym w mikroprocesorach.
Trzeba jednak wiedzieć, że pamięci o większej pojemności, powszechnie stosowane w technice komputerowej trudno byłoby nazwać rejestrami. Pamięci komputerowe realizowane są inaczej. To odrębne zagadnienie, do którego jeszcze wrócimy w ostatnim wykładzie. A teraz pora na…
Dzielniki i liczniki.
Na bazie rejestru SIPO można byłoby zrealizować licznik pierścieniowy (ring counter). Wystarczy połączyć wyjście z wejściem według rysunku 6, a potem jeden z przerzutników ustawić w stan jeden i wszystkie pozostałe wyzerować, a następnie podać taktujący sygnał zegarowy, który spowoduje, że w takim pierścieniu będzie krążyć jedynka. Uzyskujemy wtedy licznik z wyjściem zwanym 1 z N. Częstotliwość sygnału na (dowolnym) wyjściu będzie N razy mniejsza od częstotliwości sygnału wejściowego. Takie rozwiązania są wykorzystywane bardzo rzadko.
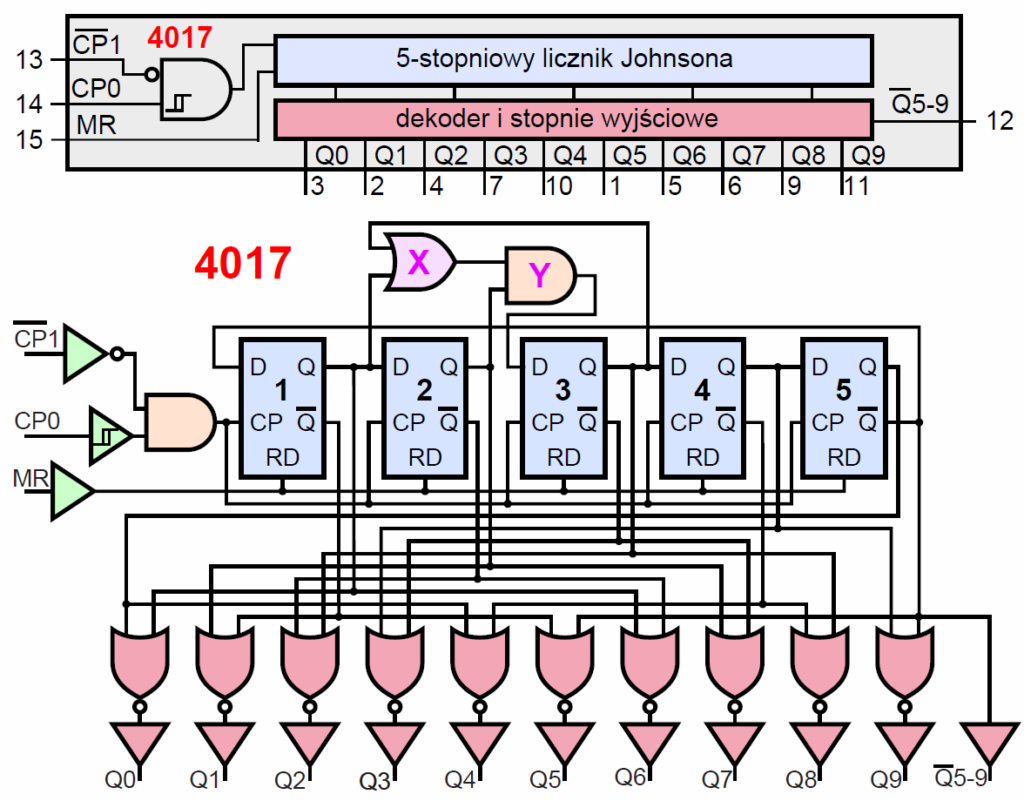
Pożyteczniejsza jest wersja licznika pierścieniowego zwana licznikiem Johnsona (czyt. dżonsona), gdzie na wejście podawany jest zanegowany sygnał z wyjścia. W zestawie masz licznik 4017, który ma taką budowę – rysunek 7. Dodatkowe bramki X, Y przywracają prawidłowa pracę po ewentualnym błędnym ustawieniu przerzutników. Oprócz samego licznika Johnsona, układ ten ma też dekodujące obwody wyjściowe typu 1 z 10, gdzie tylko na jednym z wyjść występuje stan wysoki. Kolejne impulsy zegarowe powodują przesuwanie się stanu wysokiego na kolejne wyjścia. Kostka ma obwód resetu, asynchronicznego zerowania (MR) oraz dwa wejścia, z których jedno jest wejściem bramującym, a drugie zliczającym.
Stan licznika zmieniają dodatnie, rosnące zbocza na wejściu CP0, oznaczanym też CL (przy CP1\ = L) i ujemne, opadające zbocza na „zanegowanym” wejściu CP1\ (przy CP0 = H). Na wejściu CP0 (nóżka 14) kostek praktycznie wszystkich producentów umieszczone są obwody z histerezą (wejście Schmitta), dzięki czemu może ono pracować prawidłowo także z sygnałami o małej stromości zboczy. Bardzo łatwe jest skracanie cyklu zliczania: wystarczy połączyć jedno z wyjść Q2…Q9 z wejściem zerującym MR. Przykład na rysunku 8a pokazuje zliczanie do pięciu, a ściślej od zera do czterech. Gdy stan wysoki pojawi się na wyjściu Q5 i na wejściu MR, nastąpi błyskawiczne zerowanie i zliczanie zacznie się od zera. Licznik 4017 ma też dodatkowe wyjście (nóżka 12) przydatne przy kaskadowym łączeniu kilku liczników w celu zwiększenia pojemności – rysunek 8b.
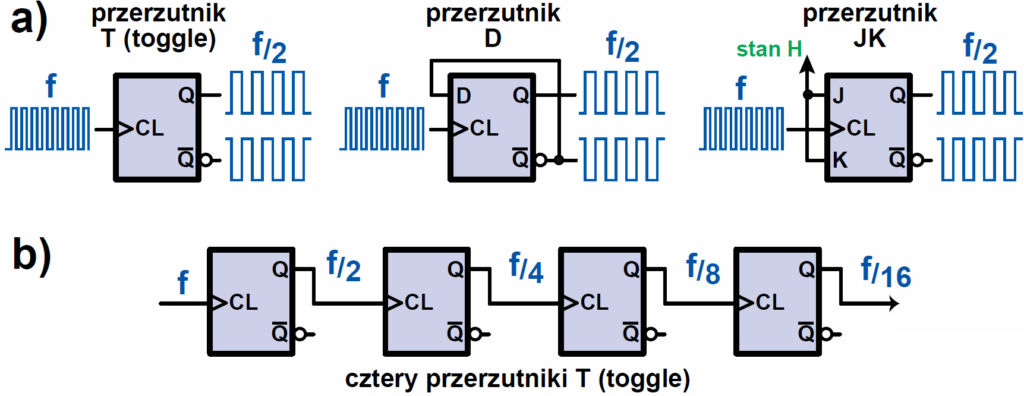
Licznik 4017 wygląda na dość skomplikowany. Najprostszym przykładem licznika jest przerzutnik toggle, czyli dwójka licząca, która dzieli częstotliwość sygnału zegarowego przez dwa – rysunek 9a. Możemy według rysunku 9b połączyć „w szereg” kilka przerzutników T, żeby każdy dzielił przez dwa częstotliwość sygnału z poprzedniego dzielnika.
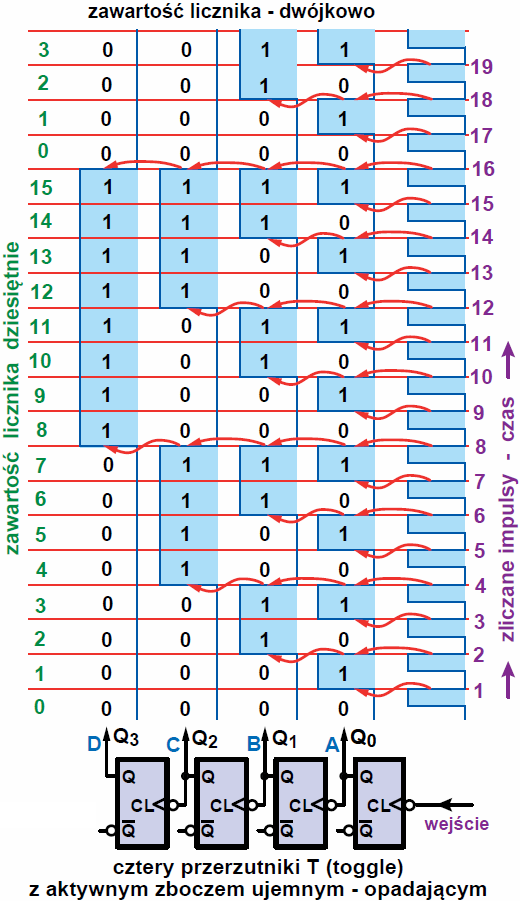
I nie jest to tylko dzielnik… Otóż wiemy już, że przerzutnik może mieć aktywne zbocze dodatnie (rosnące) albo ujemne (opadające). Rysunek 10 pokazuje układ z czterema przerzutnikami T ze zboczem aktywnym ujemnym (co sygnalizuje kółeczko na wejściu CL), gdzie stan wyjść zmienia się podczas ujemnego, opadającego zbocza sygnału zegarowego (co pokazują czerwone strzałki) oraz stany wejścia i wyjść. Celowo narysowałem wejście z prawej strony. Zwróć uwagę na zera i jedynki pojawiające się na wyjściach D, C, B, A. Kto choć trochę miał do czynienia z kodem dwójkowym czyli binarnym zauważy, że w takim liczniku pojawiają się…. kolejne liczby dwójkowe. Układ zlicza impulsy, podawane na wejście, a wynik podaje w kodzie dwójkowym.
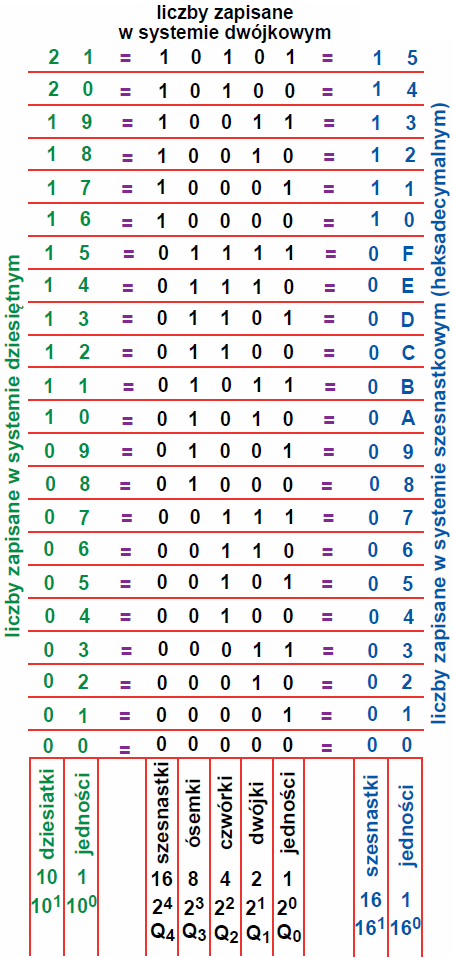
System binarny też jest systemem pozycyjnym o zasadach identycznych jak system dziesiętny. W systemie dziesiętnym mamy dziesięć cyfr (0…9), a o wartości cyfry decyduje jej pozycja. W systemie dziesiętnym mamy jednostki, dziesiątki, setki, tysiące, dziesiątki tysięcy, i tak dalej, czyli kolejne potęgi liczby 10. Analogicznie jest w systemie dwójkowym: zgodnie z nazwą, mamy tylko dwie cyfry: 0 i 1, którym w układach elektronicznych odpowiadają stany L, H, czyli brak oraz obecność napięcia. Tu też wartość danej cyfry zależy od jej pozycji: mamy jednostki, dwójki, czwórki, ósemki, szesnastki, czyli kolejne potęgi liczby 2. Ilustruje to rysunek 11.
licznik zawierający jeden przerzutnik toggle jest licznikiem dwójkowym jednobitowym i ma dwa (21) możliwe stany 0, 1. Licznik dwubitowy zawiera dwa przerzutniki T, ma cztery (22) stany i zlicza w zakresie 0…3 (dwójkowo 00…11), licznik czterobitowy ma szesnaście (24) stanów 0….15 (dwójkowo 0000…1111), a licznik 8-bitowy – 256 stanów (28). W technice cyfrowej bardzo popularne są systemy ośmiobitowe, i to nie tylko liczniki, ale też rejestry i inne układy oraz tak zwane szyny danych (zawierające osiem linii – przewodów/ścieżek. Liczbę ośmiobitową powszechnie nazywa się bajtem. W technice komputerowej często wykorzystuje się też system szesnastkowy (heksadecymalny), gdzie mamy szesnaście cyfr: oprócz 0…9 mamy dodatkowo cyfry, A =10, B=11, C=12, D=13, E=14 i F=15.
Jeżeli chodzi o oznaczenia wejść i wyjść liczników, to oznacza się je różnie: albo literami A, B, C, D…, co nie ma żadnego związku z systemem szesnastkowym, albo z wykorzystaniem indeksów liczbowych, zaczynających się od zazwyczaj zera, a nie od jedności: Q0, Q1, Q2, Q3… Indeksy te są równe potęgom liczby dwa w systemie dwójkowym – porównaj rysunki 10 i 11. Podobnie bywa w rejestrach oraz w innych układach i systemach wielobitowych – często numeracja oznaczeń wejść i wyjść zaczyna się od zera, wskazując na kolejne potęgi liczby dwa, co ma ścisły związek z kodem dwójkowym. Ale nie zdziw się, jeśli napotkasz też numerację zaczynającą się od jedynki, a nie od zera.
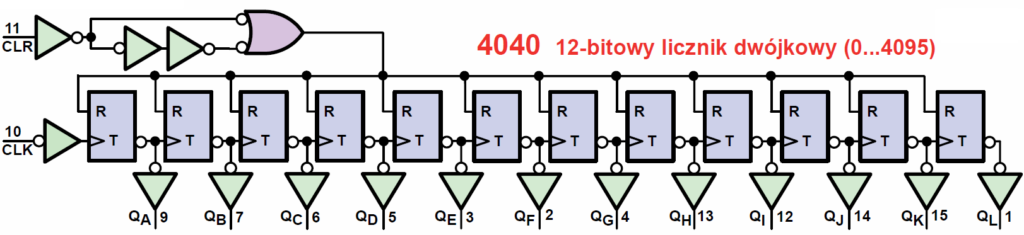
A wracając do liczników: rysunek 12 pokazuje schemat wewnętrzny 12-bitowego licznika CMOS4040. Na wyjściach (QL…QA) pojawiają się liczby dwójkowe w zakresie 0 … 4095 (dwójkowo 0 … 111111111111).
Omawiane liczniki zliczają od zera w górę. Natomiast licznik z rysunku 9b z przerzutnikami T z aktywnym zboczem dodatnim – rosnącym zlicza… w dół, od maksymalnej pojemności licznika do zera. Kierunek zliczania w liczniku z rysunku 10 można łatwo zmienić, podając na wejścia zegarowe sygnał z wyjść zanegowanych (Q\), jak pokazuje rysunek 13a i 13b. Można też zbudować liczniki dwukierunkowe – prosty przykład masz na rysunku 13c.
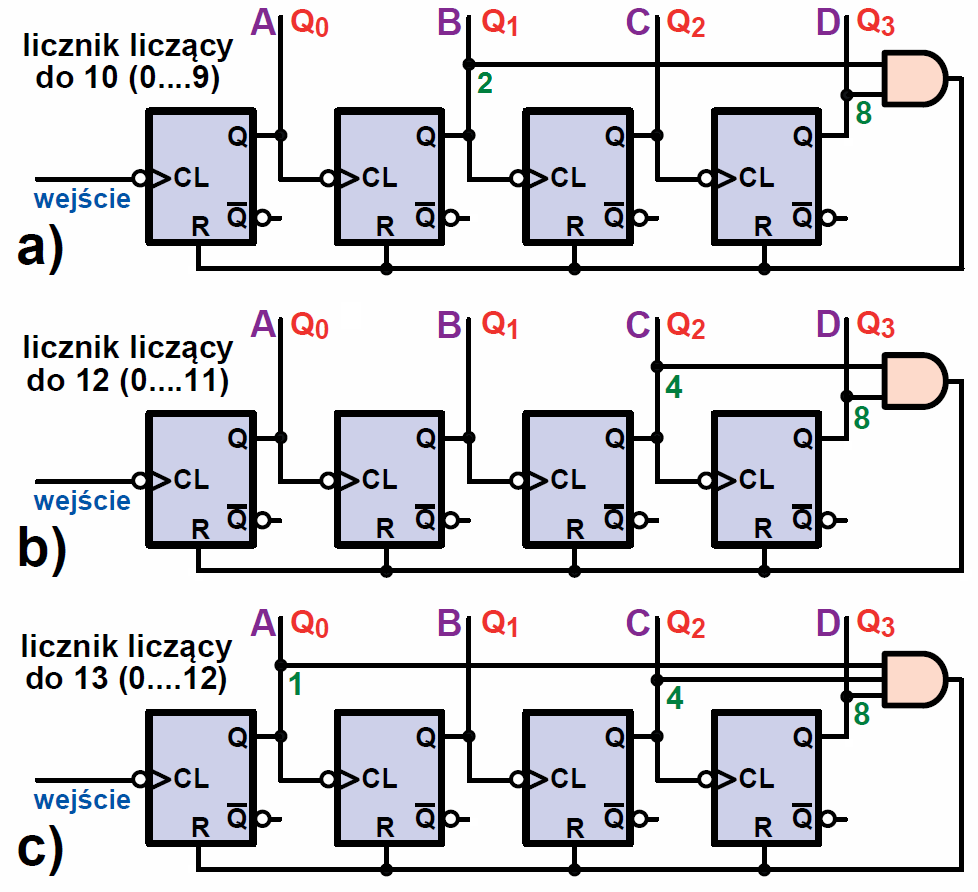
Takie liczniki zliczają w naturalnym kodzie dwójkowym, a ich pojemność jest potęgą liczby dwa. Można w prosty sposób uzyskać liczniki dwójkowe o krótszym cyklu, zerując wszystkie przerzutniki licznika, gdy dojdzie on do określonej liczby. Wystarczy do tego jedna bramka. Rysunek 14 pokazuje przykłady skracania cyklu. Na rysunku 14a mamy licznik binarny zliczający w górę do dziesięciu (0…9), nazywany licznikiem BCD (Binary Coded Decimal). Gdy w liczniku pojawi się liczba 10 (dwójkowo 1010), bramka AND błyskawicznie wyzeruje przerzutniki i liczenie zacznie się od zera. Liczniki takie (a także licznik 4017) możemy łączyć kaskadowo, czyli „szeregowo”, by zliczać jednostki, dziesiątki, setki…
Liczniki można realizować na mnóstwo sposobów, a nie tylko w oparciu o proste przerzutniki T, gdzie sygnałem zegarowym dla następnego przerzutnika jest sygnał z wyjścia przerzutnika poprzedniego. Można zrealizować liczniki z wykorzystaniem (wielowejściowych) przerzutników JK i podawać sygnał zegarowy na wejścia wszystkich przerzutników licznika. Uzyskamy wtedy tzw. liczniki synchroniczne.
Ale po co komplikować proste i eleganckie liczniki asynchroniczne?
Otóż sensowna komplikacja okazuje się korzystna, bowiem daje możliwość optymalizacji pod różnymi względami, głównie minimalizacji opóźnień. To kolejne bardzo obszerne zagadnienie – możesz w pierwszym uproszczeniu przyjąć, że liczniki synchroniczne mogą być znacząco szybsze od asynchronicznych i mają mniej wad.
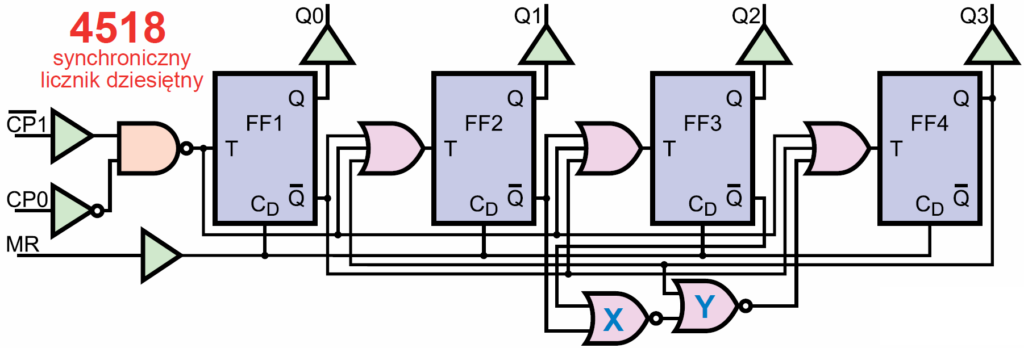
Rysunek 15 pokazuje schemat wewnętrzny licznika synchronicznego z kostki 4518, gdzie bramki X, Y skracają cykl liczenia (0…9).
Można też dodać obwody, dzięki którym licznik będzie mógł zliczać w dół, także na przykład od 9 do zera. Istnieją też różne liczniki dwukierunkowe – mają albo dodatkowe wejście, które określa kierunek zliczania, albo dwa wejścia: „dodające” i „odejmujące”. Niektóre mają możliwość wstępnego wpisywania do licznika (Preset) liczby i zliczania od tej wpisanej liczby (w górę lub w dół). Rysunek 16 pokazuje budowę popularnego licznika 4029, który jest czterobitowym licznikiem dwukierunkowym, do wyboru binarnym lub dziesiętnym (dekadowym), z możliwością synchronicznego wpisywania czterobitowej liczby z wejść J1…J4 i synchronicznego zerowania. Sprytna budowa pozwala łączyć je, by uzyskać liczniki dwójkowe lub dziesiętne (dekadowe) o dowolnie dużej pojemności.
W postaci układów scalonych rodziny CMOS4000 oraz różnych wersji rodziny 74 dostępnych jest mnóstwo różnych liczników dwójkowych i dziesiętnych, a także różnych dzielników. W praktyce dla użytkownika nie ma znaczenia, jaka jest wewnętrzna budowa licznika. Istotne są tylko pełnione funkcje oraz maksymalna częstotliwość pracy.
A teraz kilka interesujących układów do realizacji.
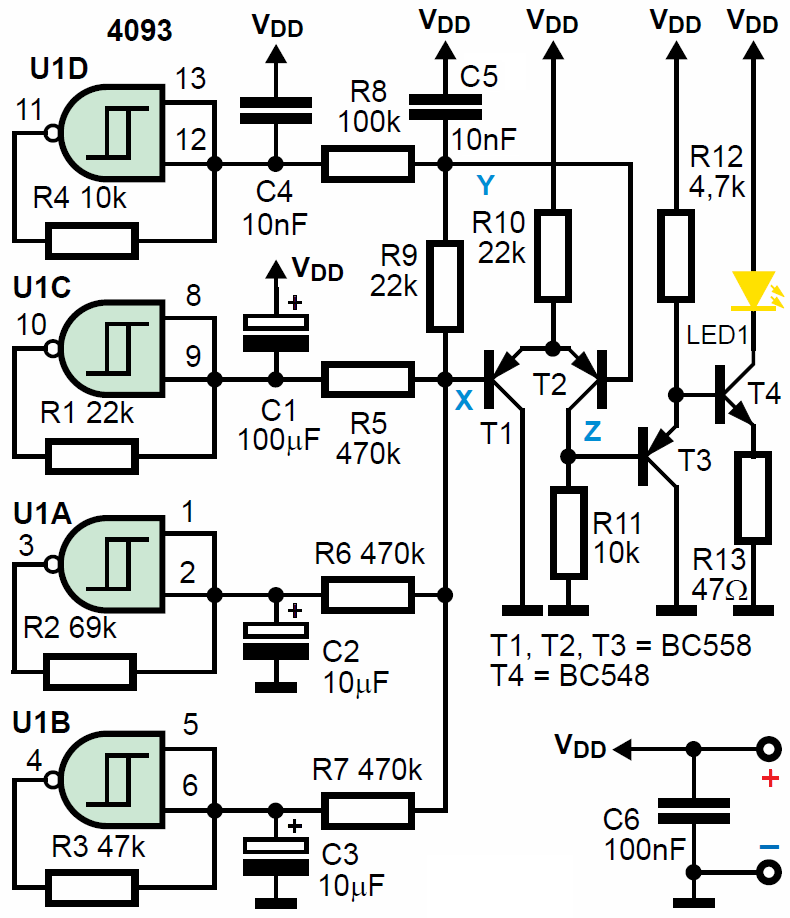
W ramach projektu tytułowego zrealizowaliśmy dwie wersje elektronicznej świeczki, gdzie do sterowania żółtej diody LED wykorzystaliśmy przebiegi prostokątne z generatorów. Podobny układ można zrealizować, wykorzystując przebiegi zbliżone do trójkąta, występujące na kondensatorach generatorów. Można to zrealizować na przykład według rysunku 17 i fotografii 18.
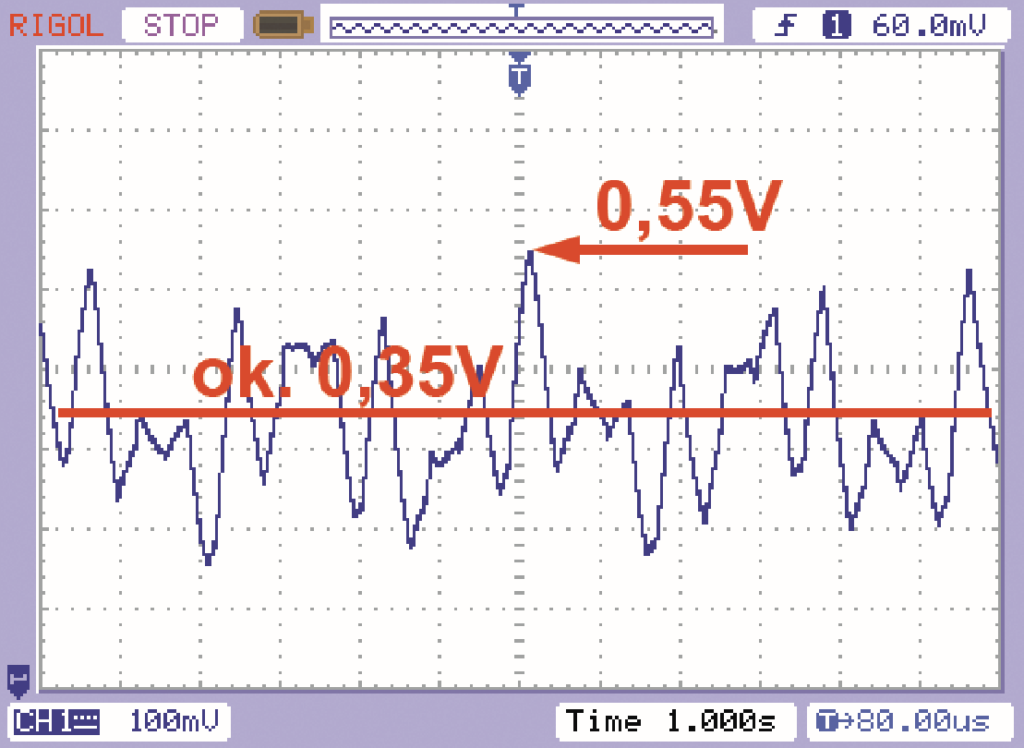
Tym razem do modulacji jasności diody LED1 wykorzystujemy przebiegi „trójkątopodobne” z trzech generatorów U1C, U1A, U1B. Są one sumowane w punkcie X za pomocą trzech rezystorów R5, R6, R7. W punkcie X otrzymujemy nieregularny, pseudoprzypadkowy przebieg, którego wartość średnia jest zbliżona do połowy napięcia zasilania, ale co jest niekorzystne, wielkość składowej zmiennej zależy od szerokości pętli histerezy użytego egzemplarza układu 4093. Z uwagi na rozrzuty parametrów, a także zależność od napięcia zasilającego, trudno byłoby uzyskać powtarzalne parametry. Aby poprawić właściwości, w układzie wykorzystany został prosty wzmacniacz różnicowy na tranzystorach T1, T2. Na jedno wejście podawany jest sygnał zmienny z punktu X, a na drugie podawane jest napięcie stałe z punktu Y. Aby średnie wartości napięć (składowa stała) były jednakowe, napięcie stałe w puncie Y jest uzyskiwane przez odfiltrowanie za pomocą R8, C5 składowej zmiennej z przebiegu z czwartego generatora U1D. Z uwagi na rozrzuty szerokości histerezy, przewidziany jest rezystor R9, który zmniejsza amplitudę sygnału zmiennego z punktu X. W punkcie Z uzyskuje się sygnał zawierający składową stałą i zmienną i sygnał ten steruje znanym już nam sterowanym źródłem prądowym z tranzystorami T3, T4, gdzie rezystor R13 wyznacza czułość przetwarzania napięcia w punkcie Z na prąd diody LED1. Dzięki obecności wtórnika T3, wejście źródła prądowego ma dużą rezystancję Rysunek 19 pokazuje napięcie w punkcie Z. Jak widać, maksymalna wartość napięcia na R11 wynosi około 0,55 V, a średnia około 0,35 V co przy wartości R13 = 47 Ω daje szczytowy prąd diody LED1 około 12 mA, a średni około 7,5 mA. W tym układzie wielkość zmian jasności diody LED można zmieniać za pomocą R9 (4,7 kΩ … 100 kΩ), a średnią jasność za pomocą R13 (10 Ω … 220 Ω).
Pseudoprzypadkowe przebiegi z kilku niezależnych generatorów można też wykorzystać do budowy elektronicznej wersji gwizdka lokomotywy parowej. Schemat może wyglądać jak na rysunku 20. Mój model jest pokazany na fotografii 21. Wartości elementów nie są krytyczne – łączyłem rezystory szeregowo (R6, R10, R11) i równolegle (R1, R5) z uwagi na ograniczenia zawartości zestawu i ze względu na wygodę montażu. Ty możesz zastosować inne wartości. Zasada jest bardzo prosta – mamy sześć niezsynchronizowanych generatorów o częstotliwościach wyznaczonych przez stałe czasowe (od największej do najmniejszej):
R3×C3 = 4,7 ms R1×C1 = 3,9 ms R6×C6 = 3,2 ms R2×C2 = 2,2 ms R5×C5 = 1,5 ms R4×C4 = 1 ms
Wartości elementów nie są krytyczne, częstotliwość maksymalna jest większa od minimalnej około 5-krotnie, a pozostałe są w miarę równo rozłożone pomiędzy nimi. Zmieszanie tych częstotliwości za pomocą rezystorów R7…R12 daje w słuchawkach dźwięk gwizdka lokomotywy parowej. Kto chciałby uzyskać wyższy, bardziej przenikliwy dźwięk, może zastosować o połowę mniejsze wartości R1…R6.
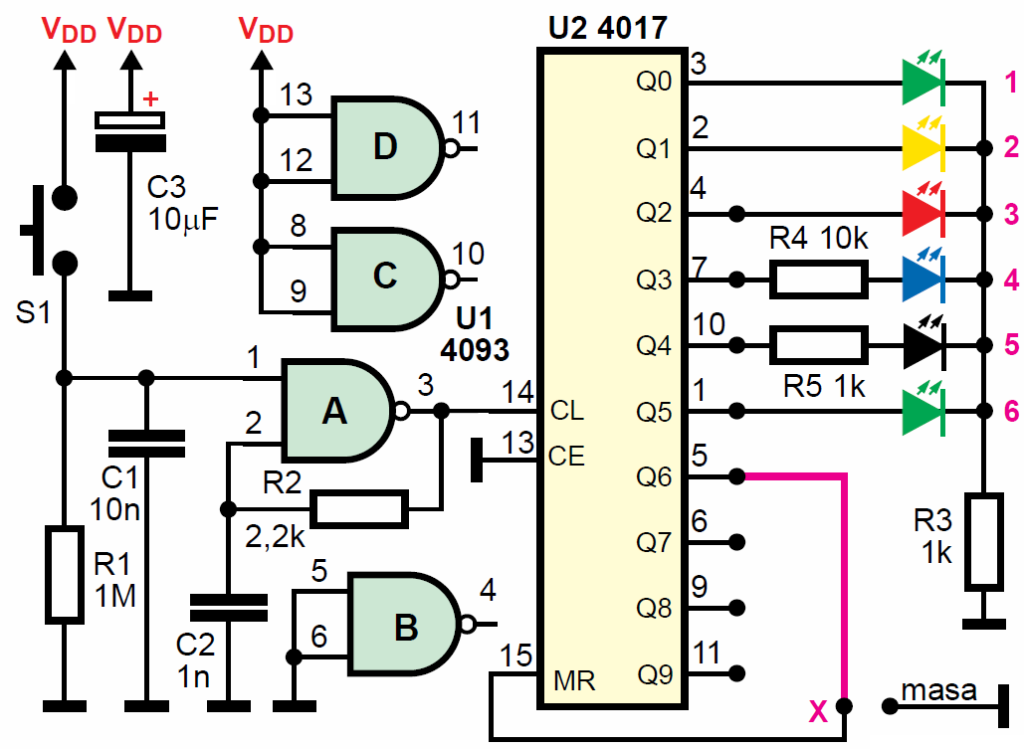
Wykorzystajmy też licznik 4017. Rysunek 22 pokazuję „maszynę losującą”. S1 może być przyciskiem lub czujnikiem dotykowym. Jego zwarcie uruchomi generator U1A o dość dużej częstotliwości (około 300 kHz). Licznik U2 zacznie szybko liczyć impulsy, co da wrażenie świecenia wszystkich diod LED. Zwolnienie przycisku S zatrzyma zliczanie i tylko jedna dioda będzie świecić, pokazując wylosowaną liczbę. Z uwagi na różny czas naciskania S1 każda próba da inną liczbę wygenerowanych impulsów.
Gdy punkt X jest dołączony do masy, układ zlicza do dziesięciu, czyli losujemy jeden z dziesięciu (wtedy diody LED powinny być dołączone do każdego z wyjść Q0…Q9). Dołączenie punktu X do jednego z wyjść Q2…Q9 pozwala skrócić cykl zliczania. Dołączenie do wyjścia Q2 (nóżka 4) daje losowanie „orzeł czy reszka”, natomiast dołączenie punktu X do wyjścia Q6 (nóżka 5) daje wynik losowania jeden z sześciu, czyli otrzymujemy nietypową elektroniczną wersję popularnej sześciennej kostki do gry. Fotografia 23 pokazuje właśnie taką wersję. Rezystory R4, R5 obniżają jasność diod niebieskiej i białej.
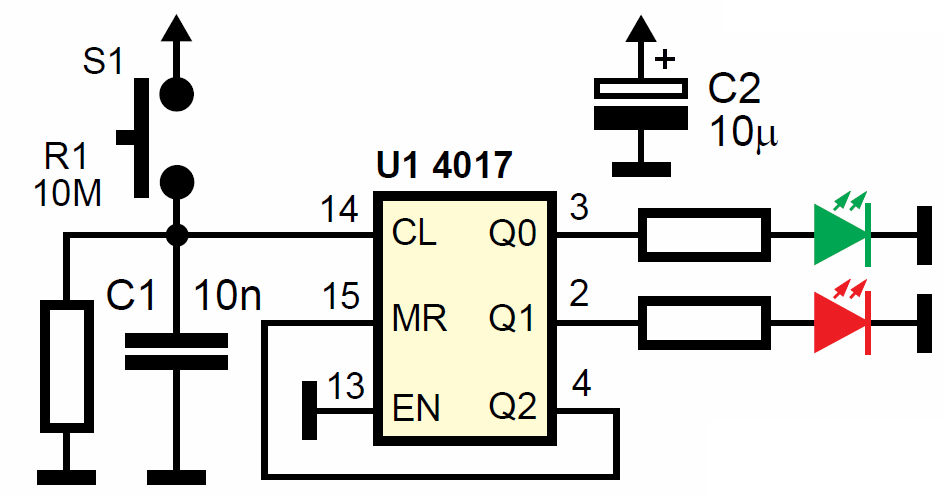
Rysunek 24 pokazuje prosty przełącznik dotykowy załącz/wyłącz. S1 może być przyciskiem albo sensorem dotykowym. Kondensator C1 likwiduje wpływ ewentualnych drgań styku, co prowadziłoby do zliczania wielu impulsów przy jednym naciśnięciu przycisku. Układ 4017 nie boi się łagodnych zboczy z kondensatora C1, ponieważ na wejściu zegarowym (nóżka 14) ma obwody histerezy.
Rysunek 25 i fotografia 26 pokazują znacznie ulepszony, inteligentny wyłącznik schodowy. Każde naciśniecie przycisku (dotknięcie sensora) powoduje zmianę stanu przekaźnika. Co ważne, obwód z kondensatorem C2 po włączeniu zasilania wyzeruje licznik oraz automatycznie wyłączy załączony przekaźnik po upływie czasu wyznaczonego przez R2C2 (około 10 sekund). Czas ten można zmieniać, stosując inne wartości C2 w zakresie 10 uF…1000 uF i R2 w zakresie 100 kΩ do 10 MΩ.
Z kolei rysunek 27 i fotografia 28 pokazują wersję prostego układu czasowego, gdzie jedno- lub wielokrotne naciśnięcie S1 włączy przekaźnik na czas wyznaczony przez R2C2. Zdecydowanie bardziej uniwersalny układ czasowy będzie głównym projektem w następnym wykładzie.
Piotr Górecki