Elektronika (nie tylko) dla informatyków (5) Kondensator – podstawowe właściwości

W poprzednim wykładzie rozprawialiśmy o potencjometrach i rezystorach SMD. W tym odcinku przyglądamy się kondensatorom i skupiamy się na ich podstawowych właściwościach.

Różniczkowanie i całkowanie (także dla początkujących)

Nie będziemy wchodzić w szczegóły, ale muszę Ci zasygnalizować pewną pożyteczną właściwość kondensatora. Otóż już wcześniej wspomniałem, że opisową zależność:

Szybkość zmian napięcia = I/C

należałoby zapisać inaczej. Oto wzory matematyczne, oddające precyzyjnie właściwości (idealnego) kondensatora:

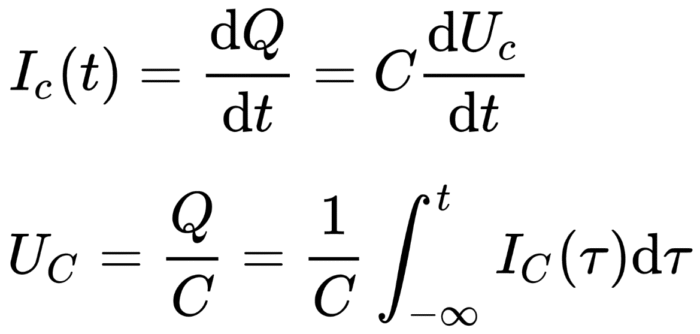
Tłumacząc najprościej, z pierwszego wynika, że jeśli wielkością „wejściową” będą zmiany napięcia, a wielkością „wyjściową” – prąd kondensatora, to chwilowa wartość prądu (wartość prądu w dowolnym momencie) jest wprost proporcjonalna do pochodnej du/dt, czyli właśnie do aktualnej szybkości zmiany napięcia. W ten sposób najzwyczajniejszy kondensator może posłużyć do… obliczania pochodnej, czyli do przeprowadzania matematycznej operacji różniczkowania.

Drugi wzór dotyczy sytuacji, gdy wielkością „wejściową” jest prąd, a „wyjściową” – napięcie. Wtedy ten sam najzwyczajniejszy kondensator pozwala przeprowadzić matematyczną operację całkowania.

I nie jest to jakaś pusta teoria. Oczywiście oprócz kondensatorów potrzebne są jeszcze inne elementy. Może się zdziwisz, ale do przeprowadzania takich operacji matematycznych, jak całkowanie, różniczkowanie, a także dodawanie, odejmowanie, mnożenie, dzielenie, potęgowanie, obliczanie pierwiastka, a nawet logarytmowanie, wystarczą rezystory i kondensatory oraz elementy czynne: diody, tranzystory i tak zwane wzmacniacze operacyjne.

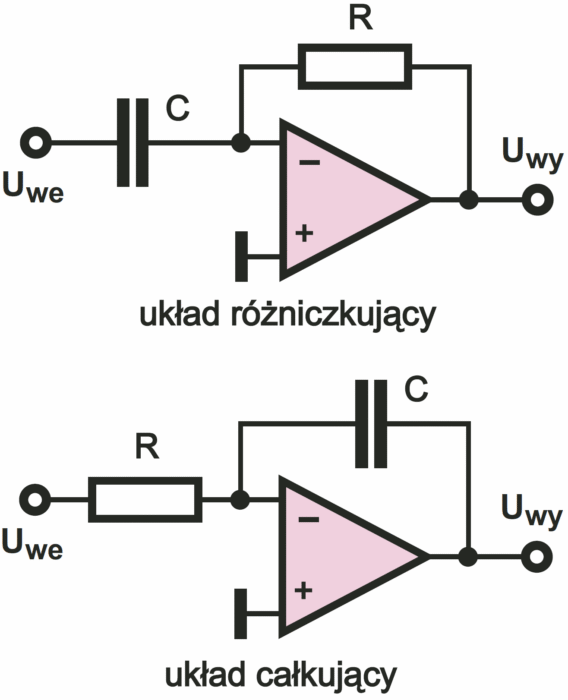
Co ciekawe, operacje całkowania i różniczkowania naprawdę można zrealizować dziecinnie łatwo. Nie musisz rozumieć szczegółów, ale dla ciekawości na rysunku 1 podaję praktyczny układ różniczkujący i całkujący, zawierające dosłownie po trzy elementy, w tym właśnie wzmacniacz operacyjny. Dziś praktycznie nie wykorzystujemy takich możliwości kondensatorów, bo wszelkie operacje matematyczne przeprowadzają w sposób cyfrowy mikroprocesory. Dlatego nie musisz wgłębiać się w szczegóły.

Ale czy wiesz, że przed opracowaniem komputerów cyfrowych (pierwszy, ENIAC 1946), powstały i przez szereg lat były praktycznie wykorzystywane komputery analogowe? Służyły głównie do obliczania torów pocisków i rakiet. Elementami czynnymi w pierwszych komputerach analogowych były oczywiście lampy elektronowe (tranzystor wynaleziono dopiero w 1948). Fotografia 2 (źródło – Wikipedia) pokazuje polski komputer analogowy AKAT-1, pierwszy na świecie tranzystorowy analizator równań różniczkowych, skonstruowany w PAN w 1959 roku przez Jacka Karpińskiego.

Oporność kondensatora

Jeszcze raz przypomnijmy fundamentalne zależności:

Szybkość zmian napięcia = I/C
I = C × Szybkość zmian napięcia

Czy widzisz tu gdzieś jakąś informację o oporności, która jest stosunkiem napięcia i prędu (U/I)?

Nie?
I słusznie!

Choć końcowe wnioski dotyczące oporności kondensatora okażą się dość proste, droga do tych wniosków taka prosta nie jest.

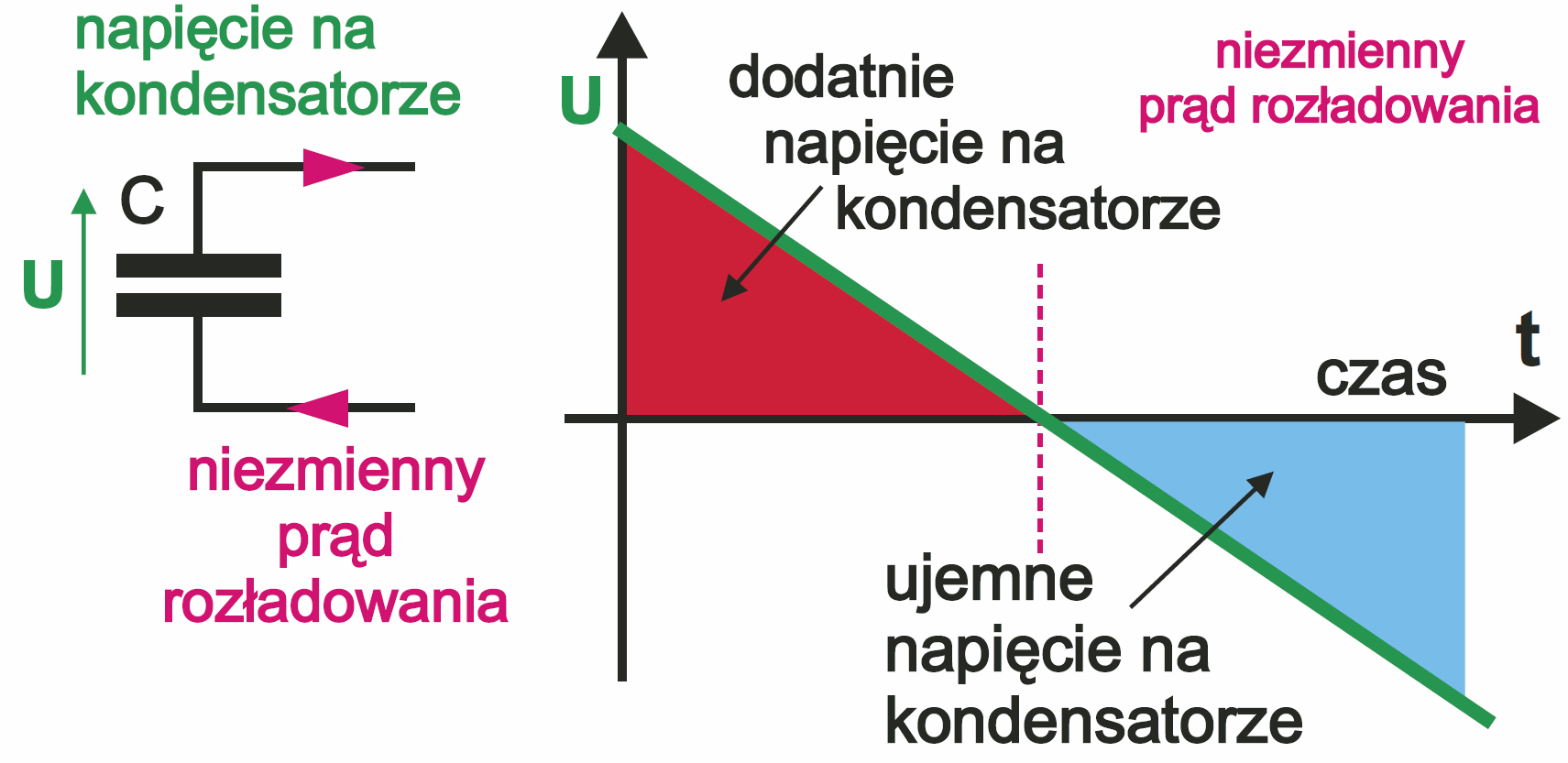
Na początek przypominam, że kierunek przepływu prądu zależy od tego, czy napięcie rośnie, czy maleje, a więc od kierunku zmian napięcia. I to jest oczywiste. A oto dodatkowy dość ważny szczegół. Wprawdzie moglibyśmy się bez tego obejść, ale od razu chcemy skoczyć na głęboką wodę, więc zajmijmy się tym: otóż w przypadku klasycznego kondensatora nie ma żadnego problemu, żeby napięcie na nim zmieniło biegunowość. Nie tylko może zmienić, ale często zmienia biegunowość. Najprościej biorąc, jeśli z dodatnio naładowanego kondensatora będzie wypływał prąd, to dodatnie napięcie będzie maleć, a po dojściu do zera zmieni biegunowość i będzie robić się coraz bardziej ujemne. Ilustruje to rysunek 3.

Tu model hydrauliczny kondensatora w postaci rury z rysunku 2a (pierwsza część tego cyklu) okazuje się niedoskonały, ponieważ trudno tam zobrazować zmianę biegunowości.

A teraz, żeby zrobić kolejny krok, załóżmy, że „przyczyną” są zmiany napięcia, a skutkiem jest prąd. Oczywiście dla danego kondensatora czym większa szybkość zmian napięcia, tym większy prąd. Na rysunku 4 masz przykłady. Wszystko jasne, prawda? Prąd odzwierciedla szybkość zmian napięcia, a kierunek prądu zależy od tego, czy napięcie rośnie, czy maleje.

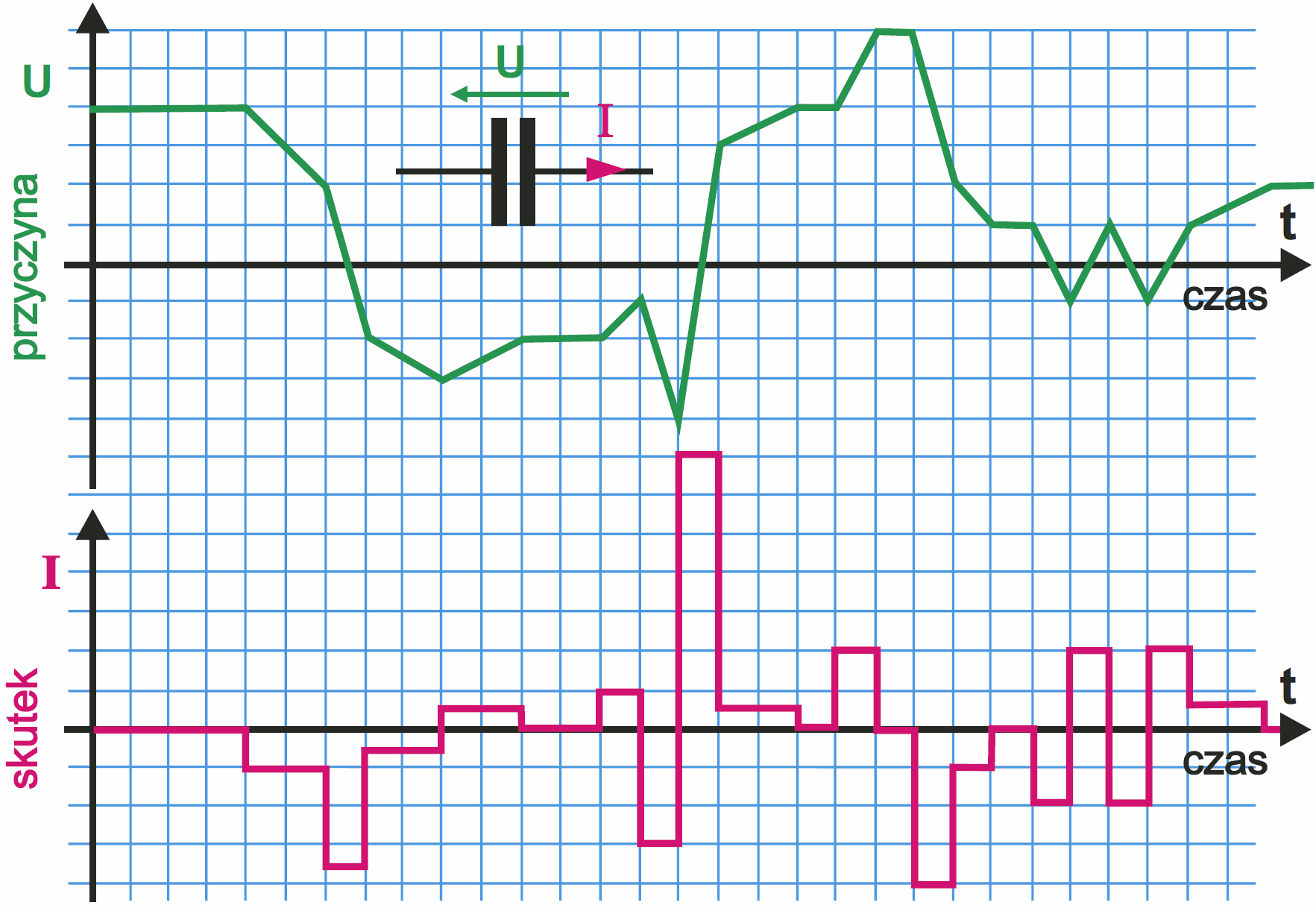
A teraz specjalnie dobrany „łamany” przebieg z rysunku 5. Czy widzisz podobieństwo obu przebiegów? Już tu można zauważyć specyficzną cechę. O ile przy przebiegach z rysunku 4 kształty prądu i napięcia były rażąco różne, o tyle rysunek 5 wskazuje, że powinien istnieć specyficzny przebieg, dla którego kształty napięcia „wejściowego” i prądu „wyjściowego” będą takie same.

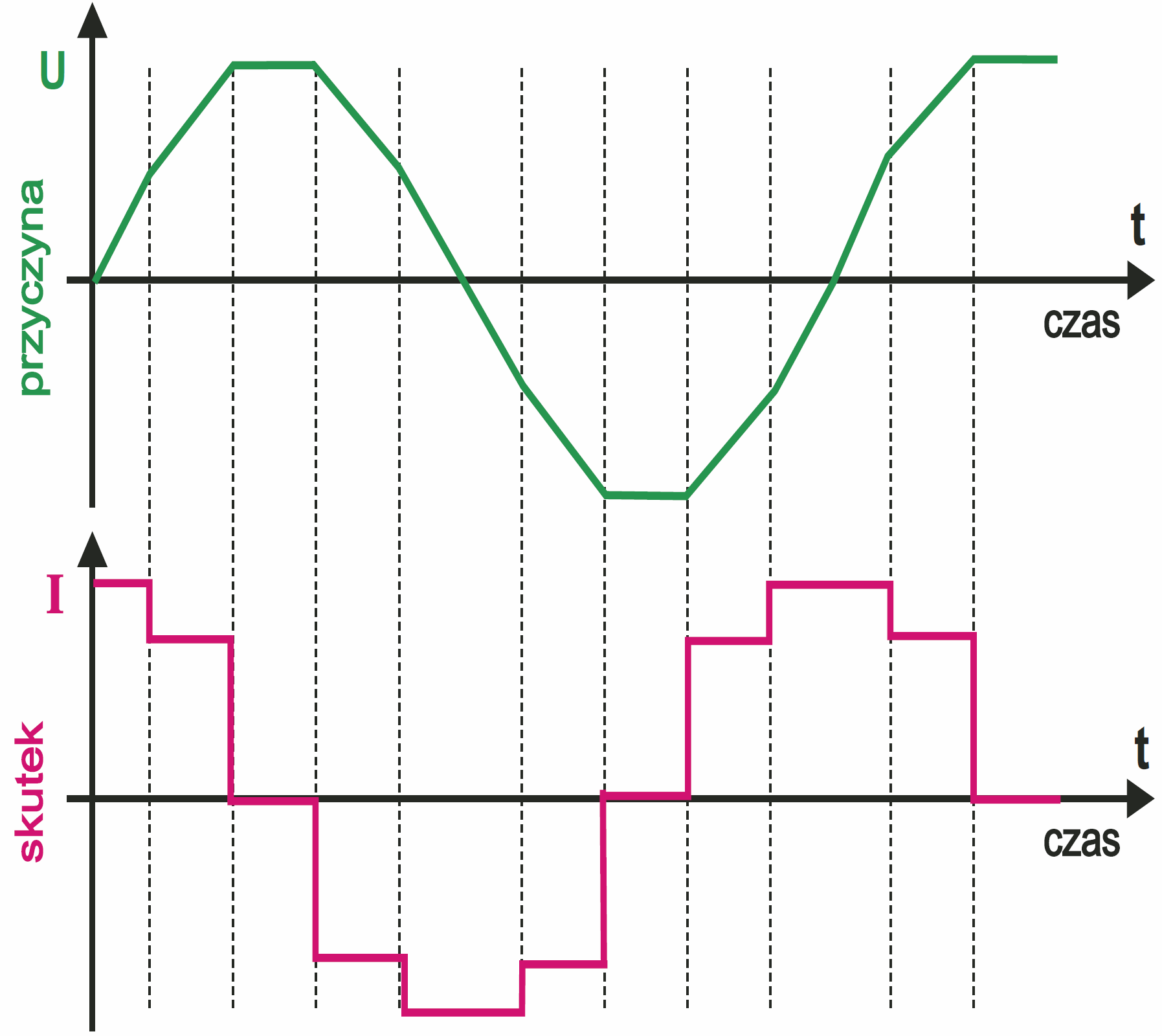
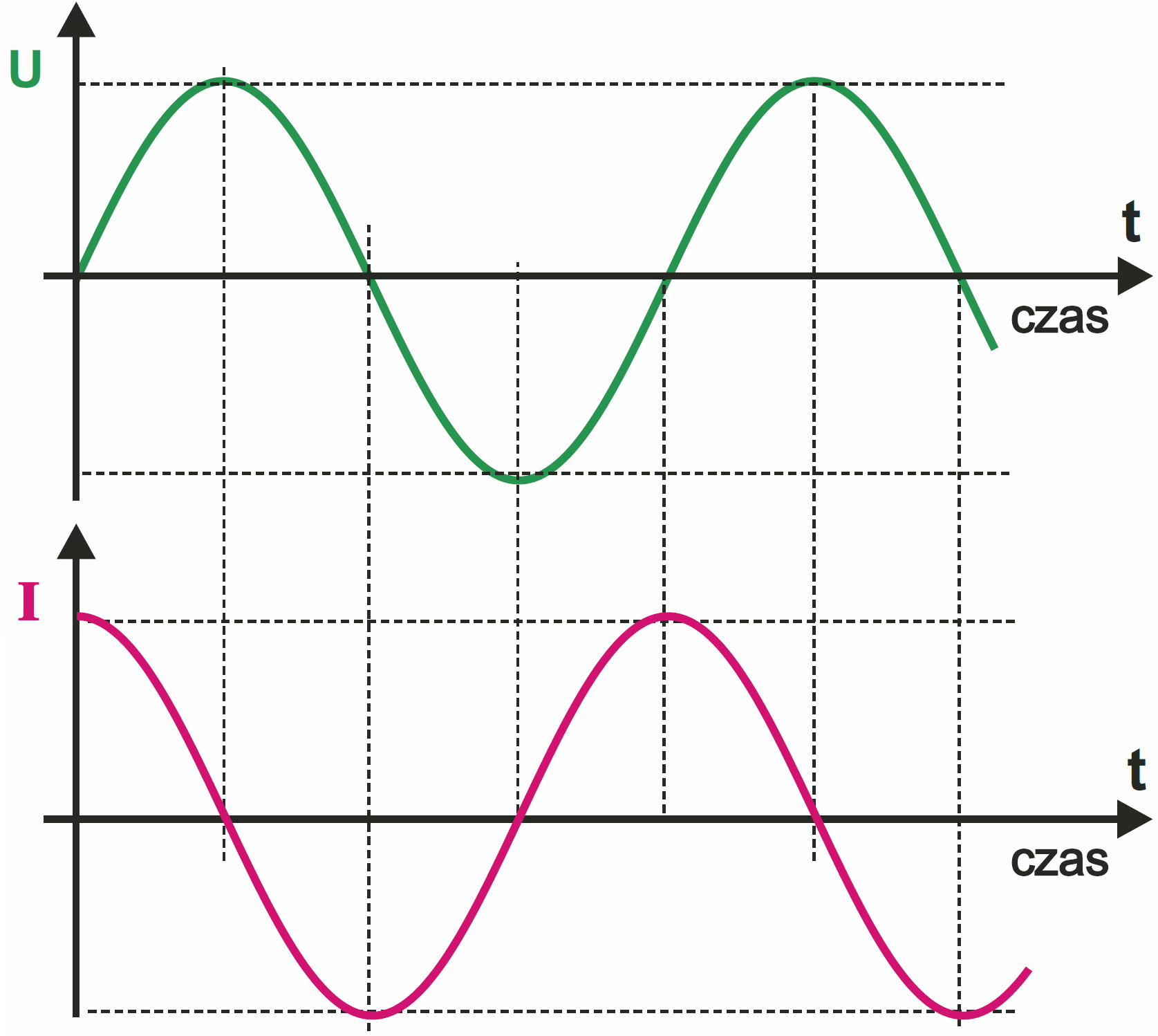
I tak jest w przypadku przebiegu sinusoidalnego – rysunek 6. Zwróć uwagę, że nadal dla dowolnej chwili wartość i kierunek prądu odzwierciedlają chwilową szybkość zmian napięcia.

A przy okazji przypomina się też wcześniejsza informacja o różniczkowaniu i całkowaniu. I tu bardziej zaawansowanym zapewne przypomnę się wzory matematyczne:

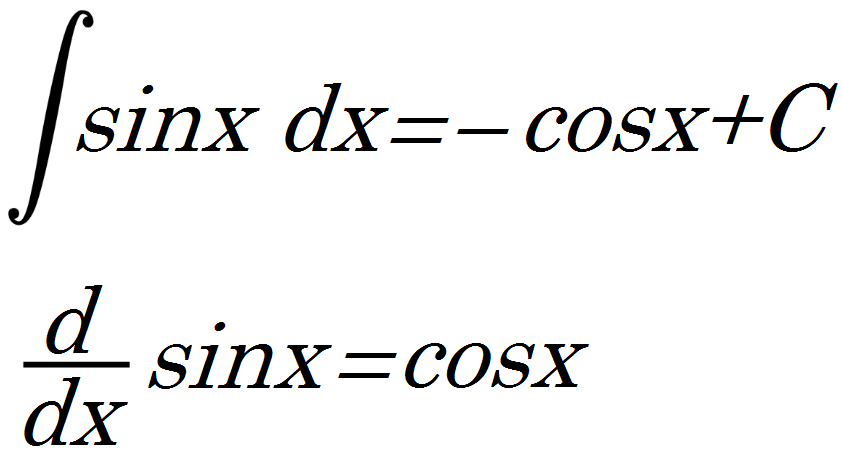
Nie przejmuj się, jeśli tych wzorów nie rozumiesz.

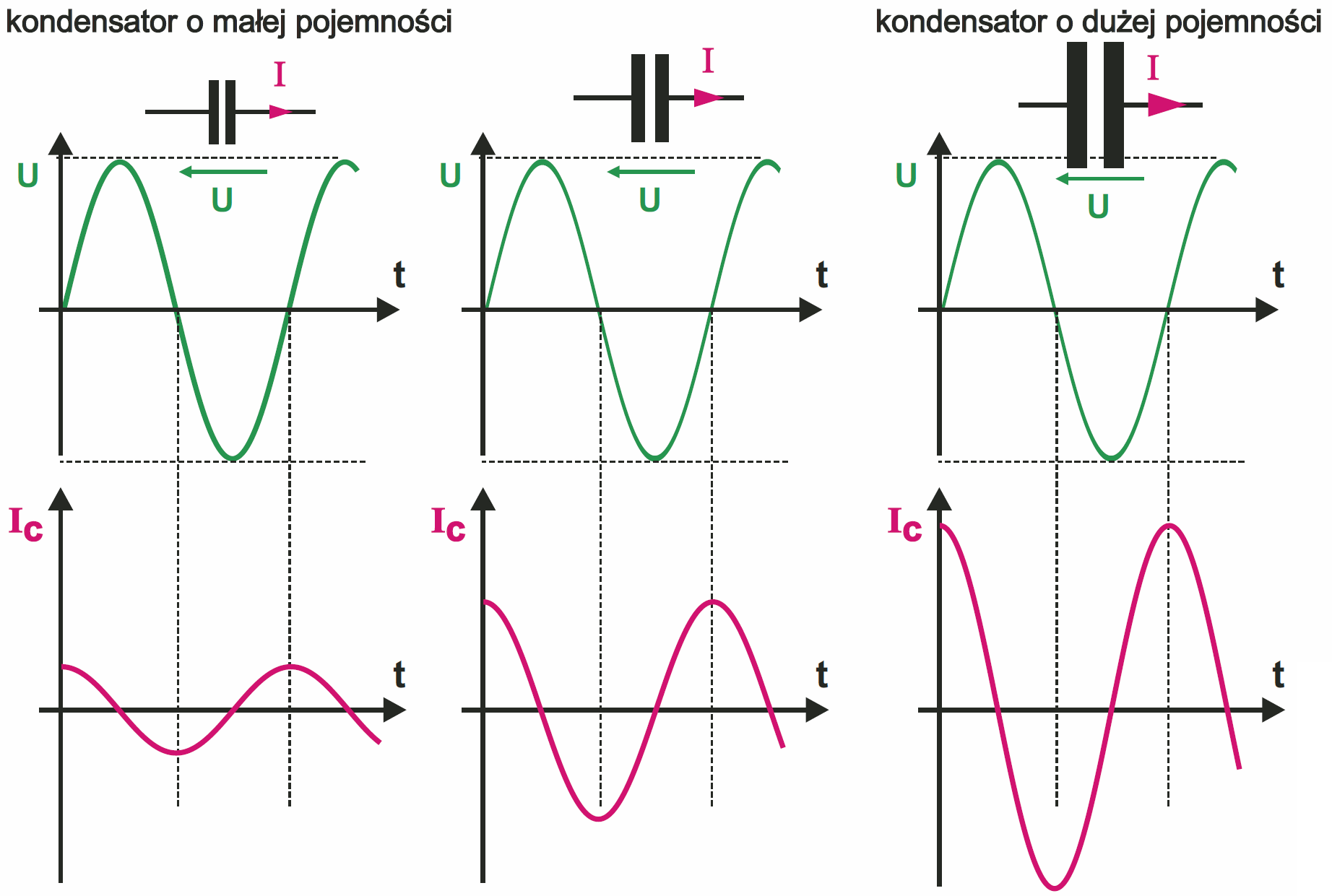
Podkreślam, że tylko w przypadku „magicznego”, jedynego w swoim rodzaju przebiegu – właśnie przebiegu sinusoidalnego, kształty napięcia i prądu są jednakowe – jeszcze raz przeanalizuj rysunki 4…6. Nieprzypadkowo mówi się, że przebieg sinusoidalny jest podstawowym, elementarnym przebiegiem w elektronice. Zapamiętaj to! A jeśli to już wiemy, zróbmy następny krok Rysunek 7 pokazuje zależność prądu od napięcia dla różnych wartości pojemności C.

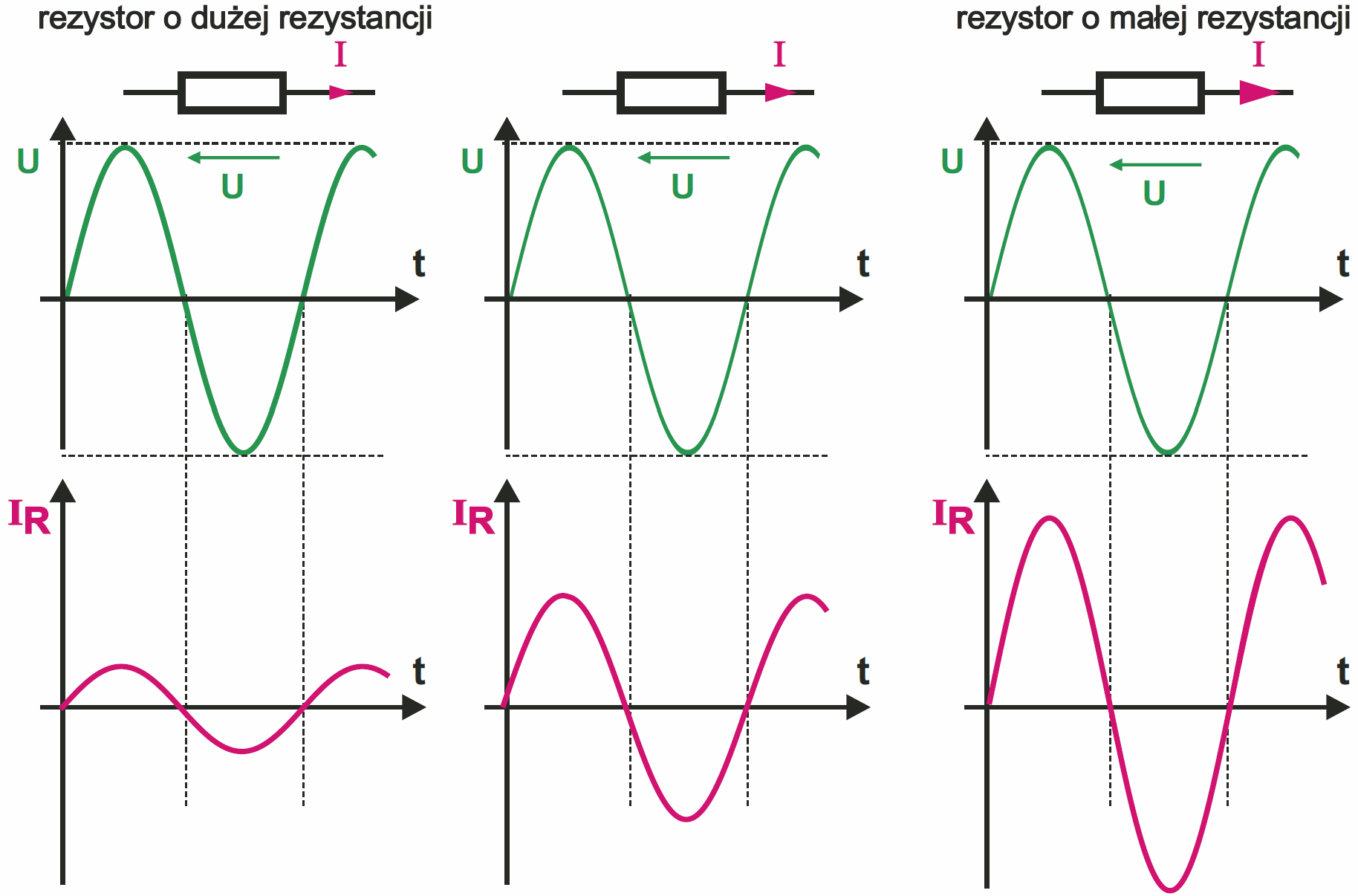
We wszystkich przypadkach „przyczyna” jest jednakowa – kształt „wejściowego” przebiegu napięcia jest taki sam. Zależnie od pojemności C inna jest wielkość „skutku” – prądu, choć kształt prądu zawsze jest sinusoidą. Może trochę niepokoi stałe przesunięcie między prądem a napięciem. Ale widać wyraźnie, że sytuacja jest bardzo podobna, jak w obwodzie z rezystorem – porównaj rysunek 8.

Przebiegi z rysunków 7 i 8 różnią się tylko jednym szczegółem – przesunięciem między prądem a napięciem. Reszta jest identyczna.

I oto jesteśmy na tropie czegoś, co można nazwać opornością kondensatora. Ale pamiętaj, że dotyczy to tylko przebiegu sinusoidalnego! Na razie z rysunku 7 widzimy, że ta oporność jest odwrotnie proporcjonalna do pojemności kondensatora.

Zanim w pełni poznamy tę dziwną oporność, musimy na chwilę zająć się przebiegiem sinusoidalnym i jego parametrami. O tym w następnym wykładzie.

Piotr Górecki