Radiowa Ośla Łączka – wektorowe zawirowania

Pole elektromagnetyczne należy chyba do najbardziej „zwektoryzowanych” działów ogólnie pojętej fizyki. Trudno jest o nim mówić bez rozumienia możliwych działań na wektorach. O tym, że wektory można dodawać uczą w szkołach podstawowych (tak było u mnie), ale to nie wszystko, można więcej.

Ze szkoły podstawowej każdy wyniósł pojęcie liczby. Niby jest to proste pojęcie, jednak próba stworzenia jego definicji już prosta nie jest. Sięgając do popularnej encyklopedii, możemy przeczytać: „Liczba – pojęcie abstrakcyjne, jedno z najczęściej używanych w matematyce.” Umiemy posługiwać się liczbami, ale mamy problem, żeby określić, co to jest liczba. Podobnie jest w geometrii z pojęciem punktu czy prostej i sprawa sprowadza się do rozumienia tego w sposób intuicyjny. Podobnie można zapytać o pojęcie wektora. Traktowanie wektora jako strzałki nie jest dobrym pomysłem, gdyż nic to nie wnosi (jak realizować operacje rachunkowe na takich strzałkach?). A może potraktować wektor jak liczbę, tylko taką liczbę skierowaną? Jak realizować działania na wektorach (w sensie rachunkowym)?

Aby nie było nieporozumień, zwykłą liczbę (nieskierowaną) nazwano skalarem.

Definicja wektora

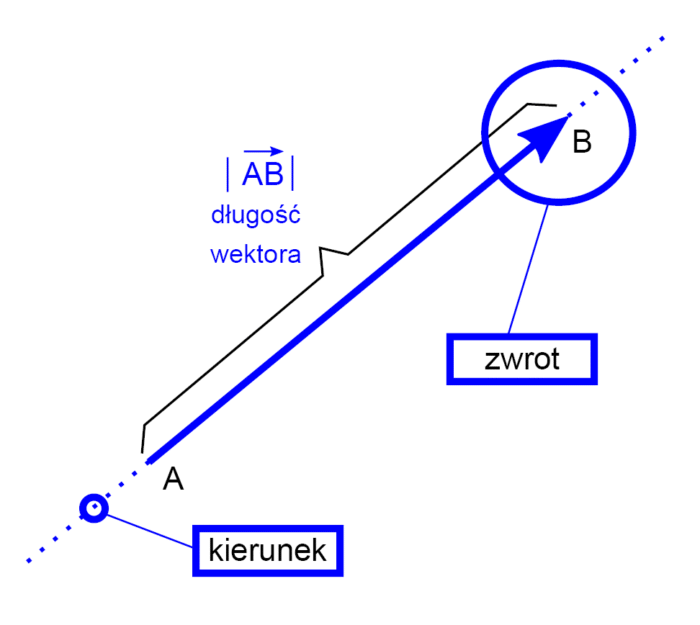
Wektor jest to uporządkowana para punktów (taki obiekt matematyczny). Punkt A jest początkiem wektora, punkt B – jego końcem. Odległość tych punktów jest nazywana długością wektora i jest oznaczana (taki odpowiednik wartości bezwzględnej w świecie skalarów). Zwrotem wektora nazywamy zwrot półprostej AB. Kierunek wektora jest kierunkiem prostej przechodzącej przez punkt A i punkt B (rysunek 1). Pomimo że pojęcie wektora zostało wymyślone głównie na potrzeby fizyki, w czystej matematyce również odgrywa istotne znaczenie.

Wiele działań algebraicznych na liczbach rzeczywistych ma swoje odpowiedniki dla wektorów: mogą być one dodawane, odejmowane, mnożone przez liczbę. Operacje te spełniają znane prawa algebraiczne: przemienności, łączności, rozdzielności (odejmowanie traktowane jest jako szczególny przypadek dodawania). Suma dwóch wektorów może być znaleziona geometrycznie za pomocą reguły równoległoboku. Mnożenie przez skalar (zwykłą liczbę) zmienia długość wektora, tzn. „rozciąga” go lub „ściska”, zachowując jego kierunek oraz jeżeli liczba jest dodatnia, zachowuje zwrot (gdy ujemna, zmienia zwrot wektora na przeciwny).

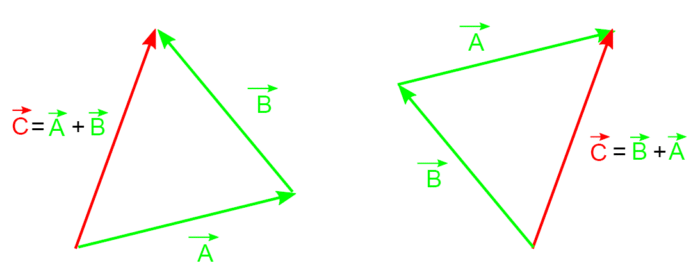
Dodawanie wektorów jest realizowane w sposób „geometryczny” (rysunek 2). Jeżeli dwa wektory stanowią dwa boki trójkąta, to sumą wektorów jest wektor utworzony przez trzeci bok tego trójkąta. Dodawanie wektorów jest przemienne (nie jest istotne, w jakiej kolejności są one dodawane).

Obok wartości skalarnych, wektory odgrywają ważną rolę w fizyce: wiele wielkości fizycznych ma reprezentację wektorową. Przykładem wielkości skalarnych jest temperatura, potencjał, praca. Wielkości wektorowe to prędkość, natężenie pola, pęd.

Składowe wektora

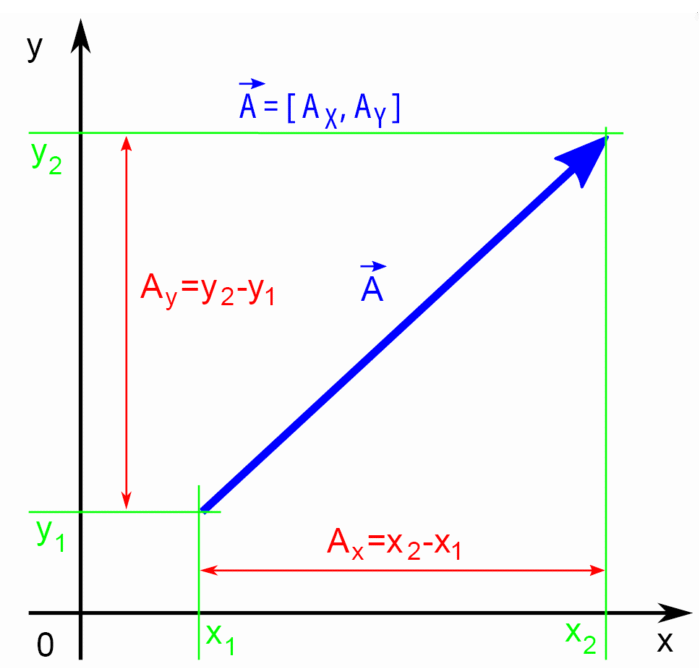
Przechodząc do „rzemiosła” wektorowego – jak prowadzić rachunki związane z wektorami? Tak jak przy operacjach na skalarach posługujemy się osią liczbową, tak w przypadku wektorów odpowiednikiem jest kartezjański układ współrzędnych (dwuwymiarowy jeżeli jest mowa o wektorach na płaszczyźnie lub trójwymiarowy dla wektorów przestrzennych). Na początek niech będzie to przestrzeń dwuwymiarowa (rysunek 3).

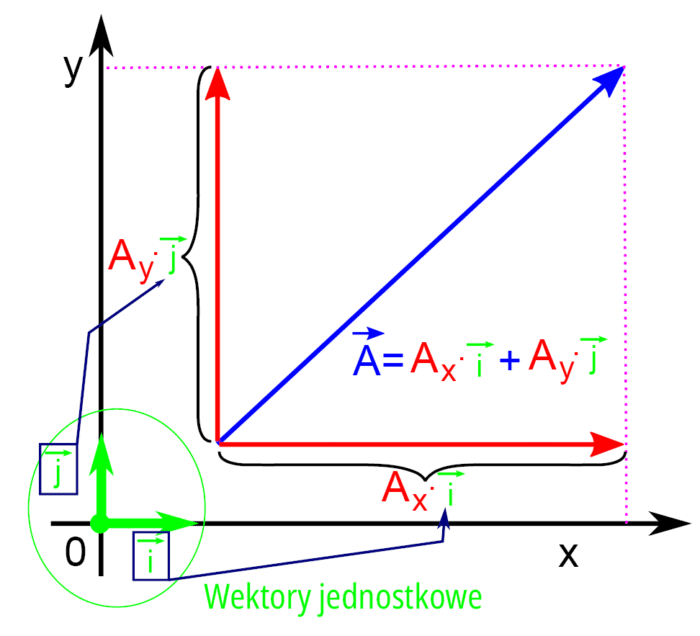
Umiejscawiając wektor w płaskim (dwuwymiarowym), prostokątnym układzie współrzędnych można go definiować parą liczb. Określają one jego współrzędne, czyli różnice pomiędzy współrzędnymi końca na osiach X i Y oraz współrzędnymi początku w określonych kierunkach. Współrzędne te są wielkościami skalarnymi, a wektor jest zapisywany następująco . W praktyce działania na wektorach znacznie lepiej jest realizować jeżeli wektor jest zapisany w bardziej intuicyjnej konwencji  (rysunek 4). Wektor jest składową finalnego wektora w kierunku osi X (jako wynik mnożenia wielkości skalarnej i wektora jednostkowego zorientowanego zgodnie z tą osią). Analogicznie jest składową w kierunku osi Y (jako wynik mnożenia wielkości skalarnej i wektora jednostkowego zorientowanego zgodnie z osią y). Gdy dodajemy je geometrycznie powstaje finalny wektor.

(…)

——– ciach! ——–

To jest tylko fragment artykułu, którego pełna wersja ukazała się w majowym numerze czasopisma Zrozumieć Elektronikę (ZE 5/2025). Pełną wersję czasopisma znajdziesz pod tym linkiem. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 5/2025 znajduje się tutaj.

Andrzej Pawluczuk
apawluczuk@vp.pl

 

Uwaga! Osoby, które nie są (jeszcze) stałymi Patronami ZE, mogą nabyć PDF-y z pełną wersję tego numeru oraz wszystkich innych numerów czasopisma wydanych od stycznia 2023, „stawiając kawę” (10 złotych za jeden numer czasopisma w postaci pliku PDF).
W tym celu należy kliknąć link (https://buycoffee.to/piotr-gorecki), lub poniższy obrazek

Następnie wybrać – Postaw kawę za:
– jeśli jeden numer ZE – 10 zł,
– jeśli kilka numerów ZE – Własna kwota. I tu wpisać kwotę zależną od liczby zamawianych numerów – wydań (N x 10 zł),
Wpisać imię nazwisko.
Podać adres e-mail.
Koniecznie zaznaczyć: „Chcę dodać dedykację/Wiadomość dla Twórcy” i tu zawsze trzeba wpisać, który numer lub numery ZE mamy wysłać na podany adres e-mailowy. Jeśli ma to być numer z tym artykułem trzeba zaznaczyć, że chodzi o ZE 5/2025.
UWAGA!!! E-mail z linkiem do materiałów (Smash) wysyłamy zazwyczaj w ciągu 24 godzin. Czasem zdarza się jednak, że trafia do spamu. Jeśli więc nie pojawi się w ciągu 48 godzin prosimy sprawdzić w folderze spam, a ewentualny problem zgłosić na adres: kontakt@piotr-gorecki.pl.