Filtry aktywne – część 1

W kilku najbliższych kilku artykułach przedstawię Ci podstawowe informacje o filtrach. Nie będziemy wgłębiać się w meandry teorii filtrów, bo to naprawdę jest bardzo trudna dziedzina.

Teoria filtrów prezentowana jest w licznych, gorszych i lepszych książkach, więc jeśli chcesz, zbadaj zagadnienie samodzielnie. Ostrzegam, że nie jest to łatwe. Jedną z przyczyn jest fakt, że warunkiem zrozumienia przedstawianych rozważań i wzorów jest znajomość wyższej matematyki, a poza tym poszczególni autorzy podchodzą do tematu z różnych stron. Szczerze mówiąc, praktykowi takiemu jak Ty, teoria nie jest potrzebna. Wystarczy, że zrozumiesz podstawowe zasady i zaprojektujesz potrzebne filtry. Jeśli chcesz, możesz wgłębiać się w teorię, by zrozumieć wszystkie szczegóły (często zadziwiające) i by z pełną świadomością projektować nawet bardzo wyszukane filtry. Ja jednak radzę Ci zacząć od praktyki.

Wiem, że nazwy, parametry, określenia i skomplikowane wzory przerażają większość elektroników. Nie bój się! Nie będę Ci tego wbijał do głowy. Nie musisz się na wszystkim znać – postarałem się z tej ogromnej masy materiału wyselekcjonować to, co dla praktyka najważniejsze.

Najpierw omówimy najważniejsze zagadnienia wstępne. Nie zlekceważ tego materiału − da Ci ogólny obraz zagadnienia. W kolejnych odcinkach podam praktyczne sposoby obliczania podstawowych rodzajów filtrów. Będą to sprawdzone, proste recepty na najpopularniejsze rodzaje filtrów. Bardziej zaawansowani znajdą dodatkowo ogólne wzory, pozwalające dobrać dodatkowe parametry.

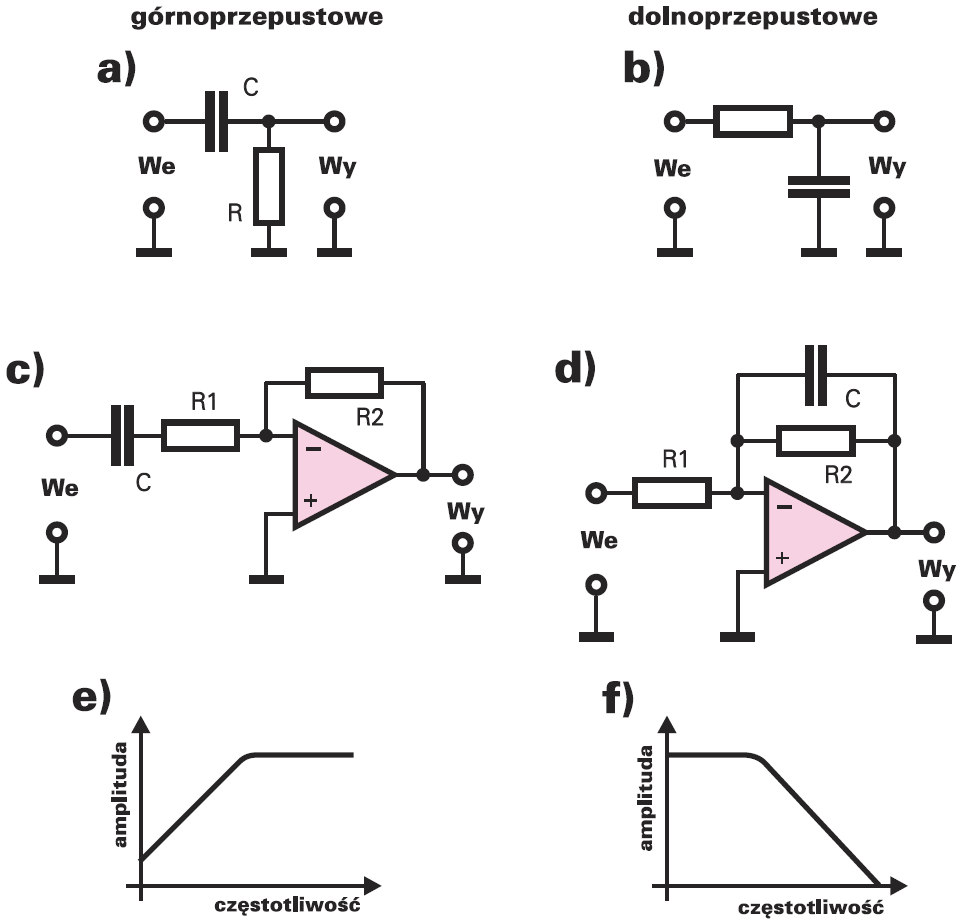
W wielu układach elektronicznych trzeba oddzielać od siebie albo tłumić składowe o różnych częstotliwościach. Potrzebne są do tego filtry. Najprostszy filtr można zbudować wykorzystując rezystor i kondensator. Rysunek 1 pokazuje prościutkie filtry górnoprzepustowy i dolnoprzepustowy oraz ich charakterystyki.

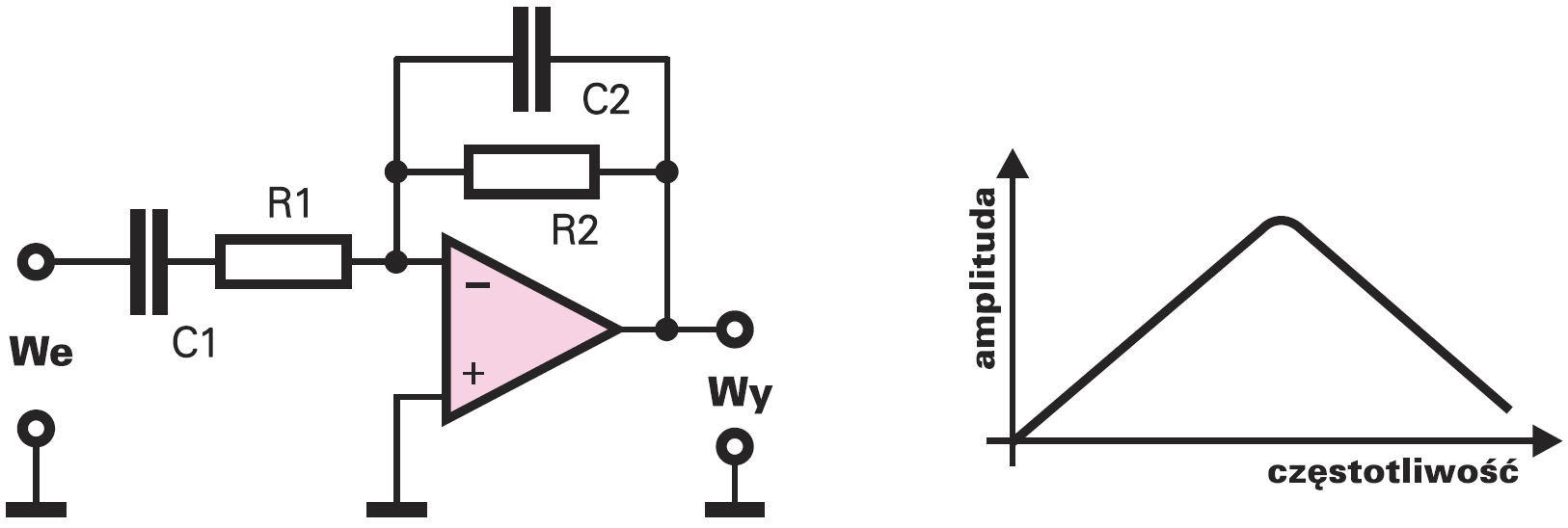
Układy ze wzmacniaczami operacyjnymi mogą dodatkowo wzmacniać sygnał. Składając filtr dolno− i górnoprzepustowy można zbudować filtr środkowoprzepustowy, czyli pasmowy. Rysunek 2 pokazuje przykładowy układ i charakterystykę.

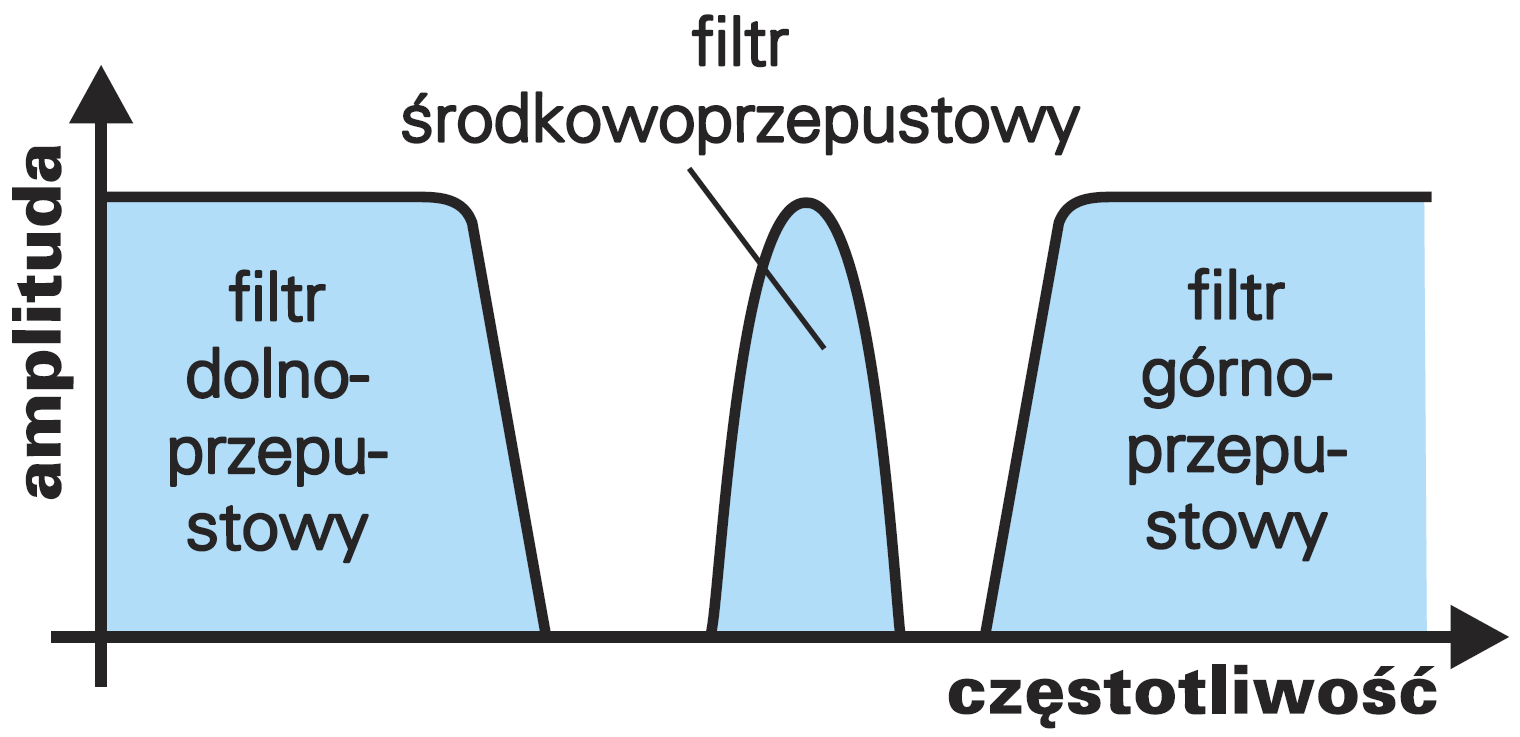
Niestety, proste filtry z rysunków 1, 2 nie są zbyt skuteczne. Są to tak zwane filtry pierwszego rzędu. Słabo tłumią sygnały spoza pasma przepustowego. Charakterystyki najprostszych filtrów mają łagodne zbocza, tymczasem dobre filtry powinny mieć charakterystyki ostre, jak na przykład na rysunku 3, gdzie na jednym wykresie zaznaczyłem charakterystyki trzech filtrów.

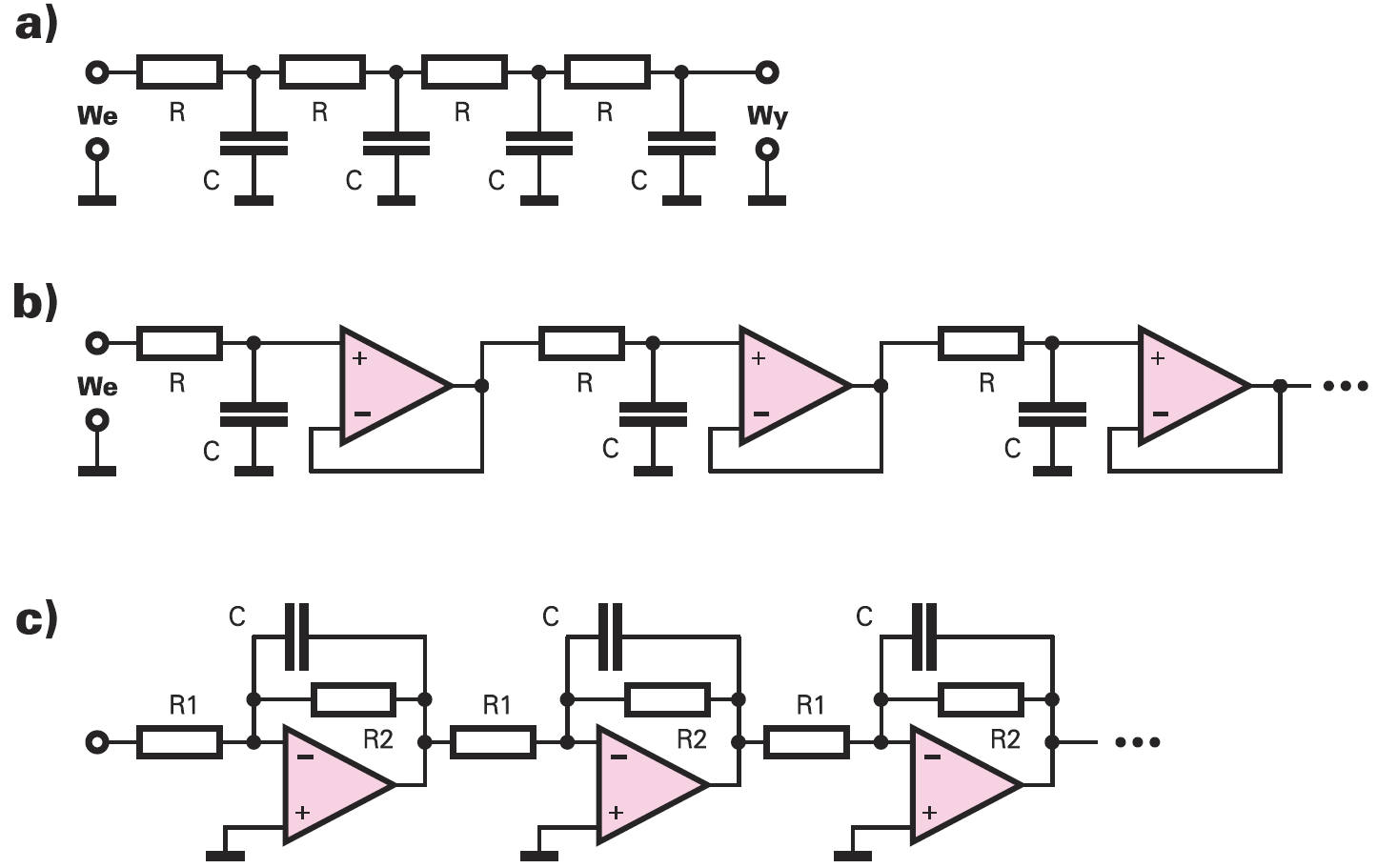
Nie można radykalnie poprawić stromości charakterystyki, łącząc kilka jednakowych ogniw RC. Rysunek 4a pokazuje ideę na przykładzie filtru dolnoprzepustowego. Niestety, kolejne ogniwa obciążają poprzednie i na pewno nie tędy droga do dobrego filtru. Niezbyt dobrym pomysłem jest też dodanie wtórników−buforów separujących ogniwa według rysunku 4b albo zastosowanie kilku ogniw według rysunku 4c. Co prawda można w ten sposób uzyskać znaczną stromość, ale na krańcach pasma przepustowego powstanie łagodne “kolano” – załamanie charakterystyki na krańcach pasma jest zdecydowanie zbyt łagodne.

Szersza analiza nie jest konieczna – wniosek jest prosty: aby uzyskać filtr o charakterystyce zbliżonej do prostokąta, trzeba wykorzystać układy nieco bardziej złożone niż te z rysunku 1b, 1d i zastosować odpowiednio dużą liczbę takich układów.

Dawniej skuteczne filtry realizowano z użyciem cewek i kondensatorów. Były to tak zwane filtry LC. Obecnie filtry LC stosuje się tylko w zakresie wysokich częstotliwości. Natomiast filtry na zakres małych częstotliwości, w tym częstotliwości akustycznych, z powodzeniem realizuje się wykorzystując wzmacniacze operacyjne oraz odpowiednio dobrane obwody RC w pętli sprzężenia zwrotnego. Są to tak zwane filtry aktywne. Dzięki zastosowaniu wzmacniacza operacyjnego możliwe jest wyeliminowanie niewygodnych cewek.

Początkujący pytają, jak to się dzieje, że wzmacniacz operacyjny poprawia sytuację i eliminuje cewki? Pełna odpowiedź nie byłaby łatwa do zrozumienia. Z grubsza biorąc, dzięki odpowiedniej pętli sprzężenia zwrotnego wzmacniacz coś dodatkowo dodaje albo dodatkowo ujmuje i poprawia charakterystykę, a nawet ją radykalnie zmienia.

Nie pomyśl jednak, że jeden jedyny wzmacniacz operacyjny rozwiązuje problem stromości zboczy. W praktyce często wykorzystujemy podstawowe moduły nazywane ogniwami, zawierające jeden wzmacniacz operacyjny i kilka elementów RC. W wielu sytuacjach wystarczy jedno ogniwo. Jeśli filtr ma mieć ostrzejsze zbocza, musi zawierać kilka takich ogniw.

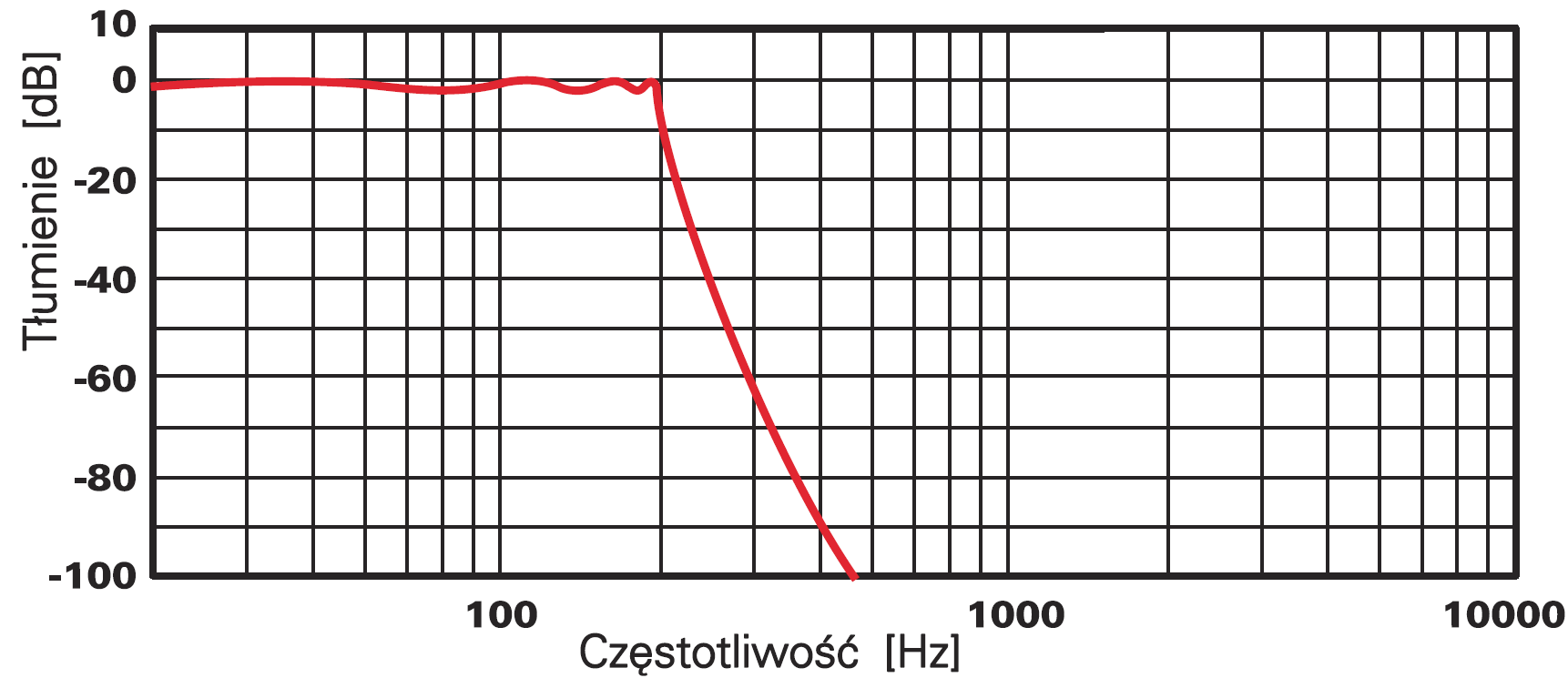
Rysunek 5 pokazuje charakterystykę pewnego filtru.

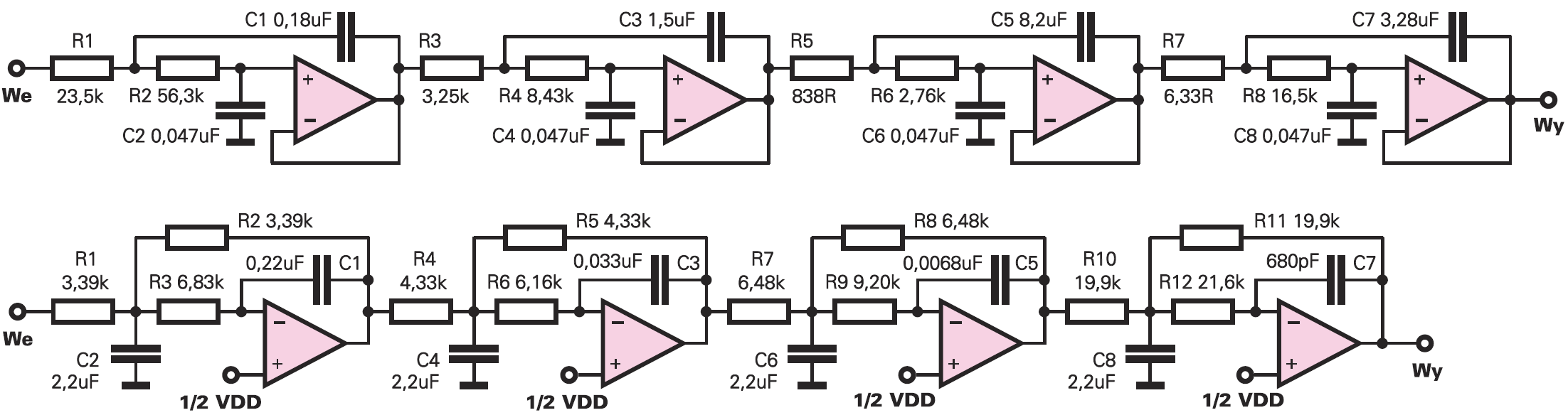
Rysunek 6 pokazuje dwa układy, które mają taką właśnie charakterystykę. Zwróć uwagę na obecność w każdym filtrze czterech podstawowych ogniw.

Tu mógłbym przygwoździć Cię informacją, że są to filtry LP ósmego rzędu o częstotliwości 3−decybelowej równej 200 Hz. Jeden z nich jest filtrem Sallen−Keya, a drugi filtrem MFB (z wielokrotnym sprzężeniem zwrotnym). Oba są filtrami Czebyszewa o falistości charakterystyki 2 dB…

Nadążasz?

Takie i podobne określenia, spotykane w książkach i czasopismach, skutecznie odstraszają od filtrów nie tylko początkujących. Nie przestrasz się ich! Spróbujmy najpierw uporządkować podstawowe pojęcia związane z filtrami.

LP, BP, HP

W literaturze na temat filtrów niewątpliwie napotkasz skróty LP, BP, HP. Pochodzą one od angielskich określeń:
LP – Low Pass – dolnoprzepustowy
BP– Band Pass – pasmowo−przepustowy (środkowoprzepustowy)
HP– High Pass – górnoprzepustowy
Być może też spotkasz określenia bandstop – pasmowo−zaporowy i allpass – wszechprzepustowy.

Częstotliwości graniczne, pasmo

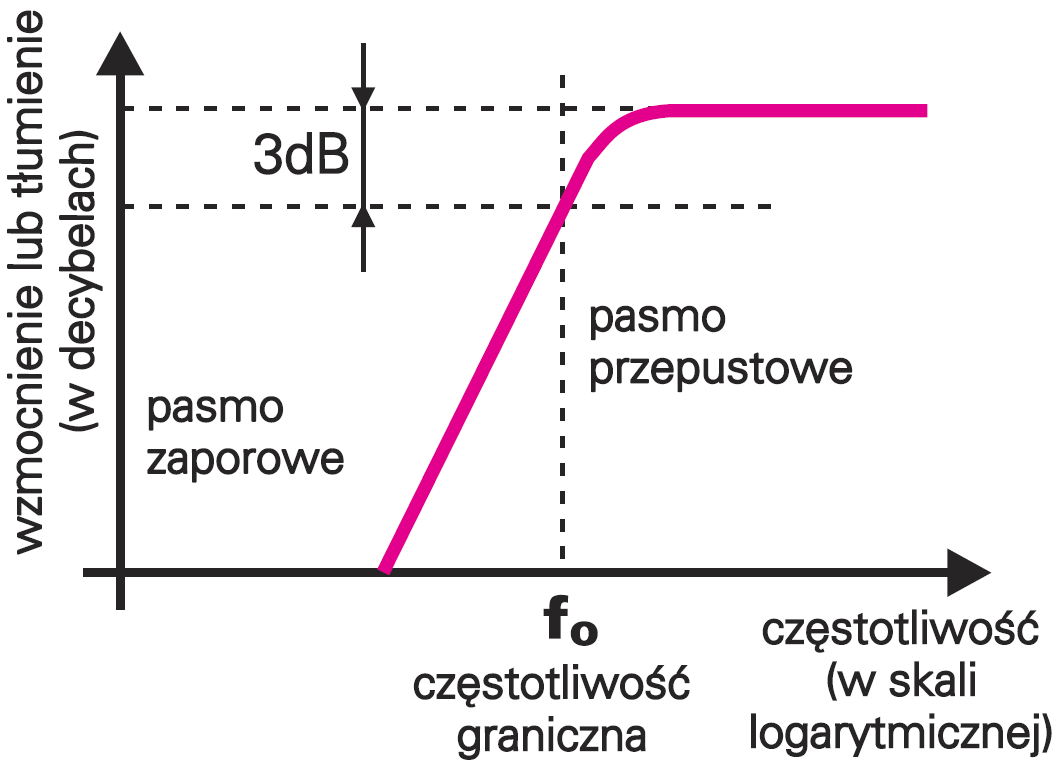
Na wykresach zazwyczaj częstotliwość i tłumienie zaznaczamy w skali logarytmicznej. Wartości tłumienia czy też wzmocnienia (w tym artykule ogólnie: amplituda) podane są w decybelach. Jednym z najważniejszych parametrów filtru jest częstotliwość graniczna (lub częstotliwości graniczne). Jako częstotliwość graniczną uznaje się częstotliwość, przy której wzmocnienie jest o 3 decybele mniejsze, niż największe wzmocnienie w paśmie przepustowym. Rysunek 7 ilustruje najważniejsze parametry związane z charakterystyką amplitudową.

Rząd filtru

Prościutki filtr z rysunku 1a czy 1b to w sumie dzielnik napięcia, gdzie jeden z elementów jest kondensatorem. Reaktancja kondensatora wyraża się znanym wzorem:

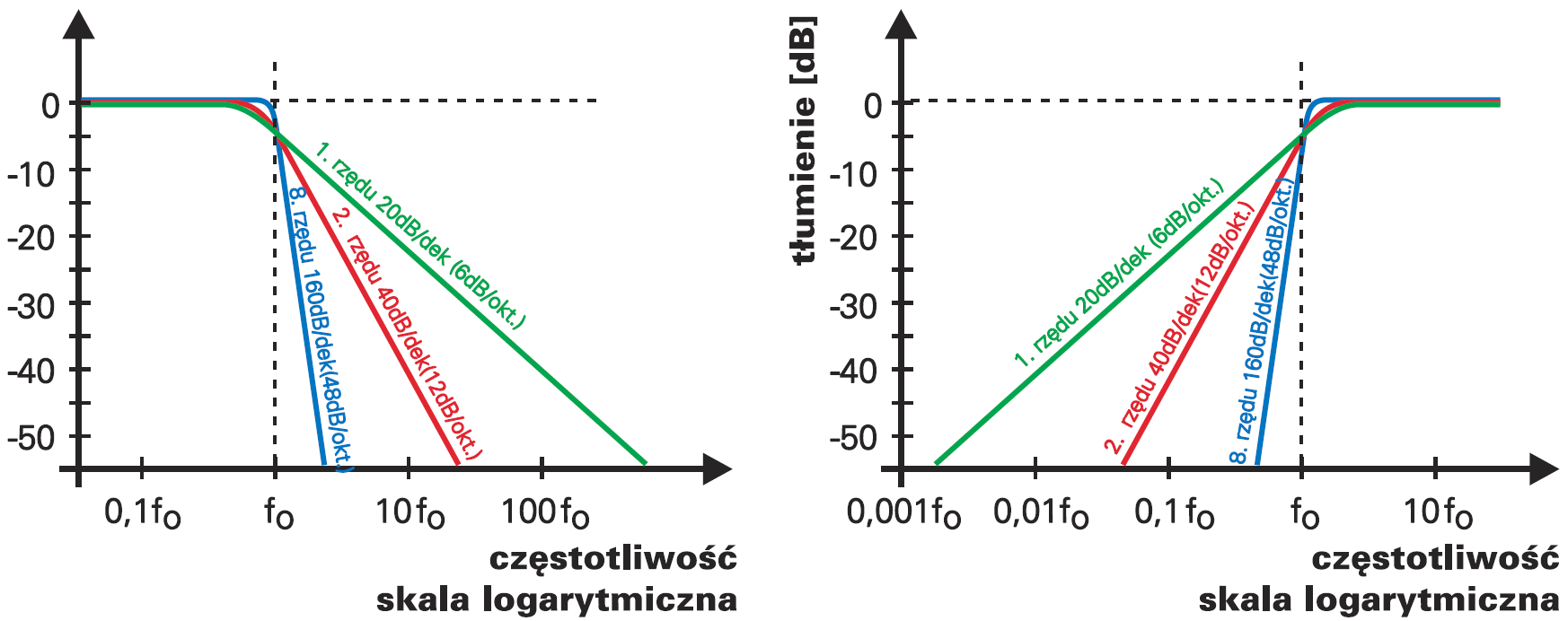
Już to pokazuje, że przy dwukrotnym (o oktawę) wzroście częstotliwości f, reaktancja Xc zmniejszy się dwukrotnie (o 6 decybeli). Przy dziesięciokrotnej zmianie częstotliwości (o dekadę), reaktancja też zmienia się dziesięciokrotnie (o 20 decybeli). Zależność taka powoduje, że najprostsze filtry pokazane na rysunku 1 mają poza pasmem przepustowym ściśle określoną stromość charakterystyki. Fachowo ujmujemy to następująco: tłumienie w paśmie przejściowym i zaporowym prostego filtru wg rysunku 1 zmienia się z szybkością 20 dB/dekadę, czyli 6 dB/oktawę. Mówimy, że są to filtry pierwszego rzędu. Ilustrują to zielone krzywe na rysunku 8. Na rysunku tym znajdziesz charakterystyki filtrów dolno− i górnoprzepustowych o częstotliwości granicznej f_o i różnych stromościach charakterystyki.

W praktyce wzmacniacz operacyjny współpracuje w dwoma, a czasem trzema kondensatorami). Zapamiętaj, że typowe ogniwa filtrów górno− i dolnoprzepustowych (na przykłąd te z rysunku 6) mają dwukrotnie większą stromość charakterystyki. Jeden wzmacniacz operacyjny pozwala łatwo zrealizować filtr o nachyleniu zbocza 40 dB/dekadę (12 dB/oktawę), czyli tak zwany filtry drugiego rzędu. Na rysunku 8 są to krzywe czerwone.

Filtr trzeciego rzędu ma stromość 60 dB/dekadę (18 dB/okt), a np. filtr 8. rzędu – 160 dB/dek. (48 dB/okt.). Charakterystyki filtrów 8. rzędu zaznaczyłem na rysunku 8 kolorem niebieskim. Można je uzyskać w układach z rysunku 6, stosując odpowiednie wartości elementów RC. Ogólnie biorąc, czym bardziej stroma ma być charakterystyka, tym więcej ogniw, czyli filtr wyższego rzędu trzeba zastosować.

Określenie rząd filtru związane jest z matematycznymi sposobami opisu charakterystyki; nie zawracaj sobie tym głowy.

A w kolejnym odcinku będziemy się zajmować innymi ważnymi parametrami filtrów.

Piotr Górecki