Filtry aktywne – część 2

W poprzednim odcinku zapoznałem Cię z podstawami na temat filtrów. W ramach artykułu tego omówimy kolejne najważniejsze zagadnienia. Nie zlekceważ tego materiału − da Ci ogólny obraz zagadnienia. Dopiero po omówieniu podstaw, w kolejnych odcinkach podam praktyczne sposoby obliczania podstawowych rodzajów filtrów. Będą to sprawdzone, proste recepty na najpopularniejsze rodzaje filtrów. Bardziej zaawansowani znajdą dodatkowo ogólne wzory, pozwalające dobrać dodatkowe parametry. A na razie kontynuujemy omawianie kluczowych parametrów filtrów.

Inne parametry

Choć charakterystyka amplitudowa zwykle jest najważniejsza, nie pokazuje wszystkich parametrów filtru. Ty projektując jedynie proste filtry na razie nie musisz przejmować się wszystkimi parametrami. Warto jednak mieć o nich ogólne pojęcie.

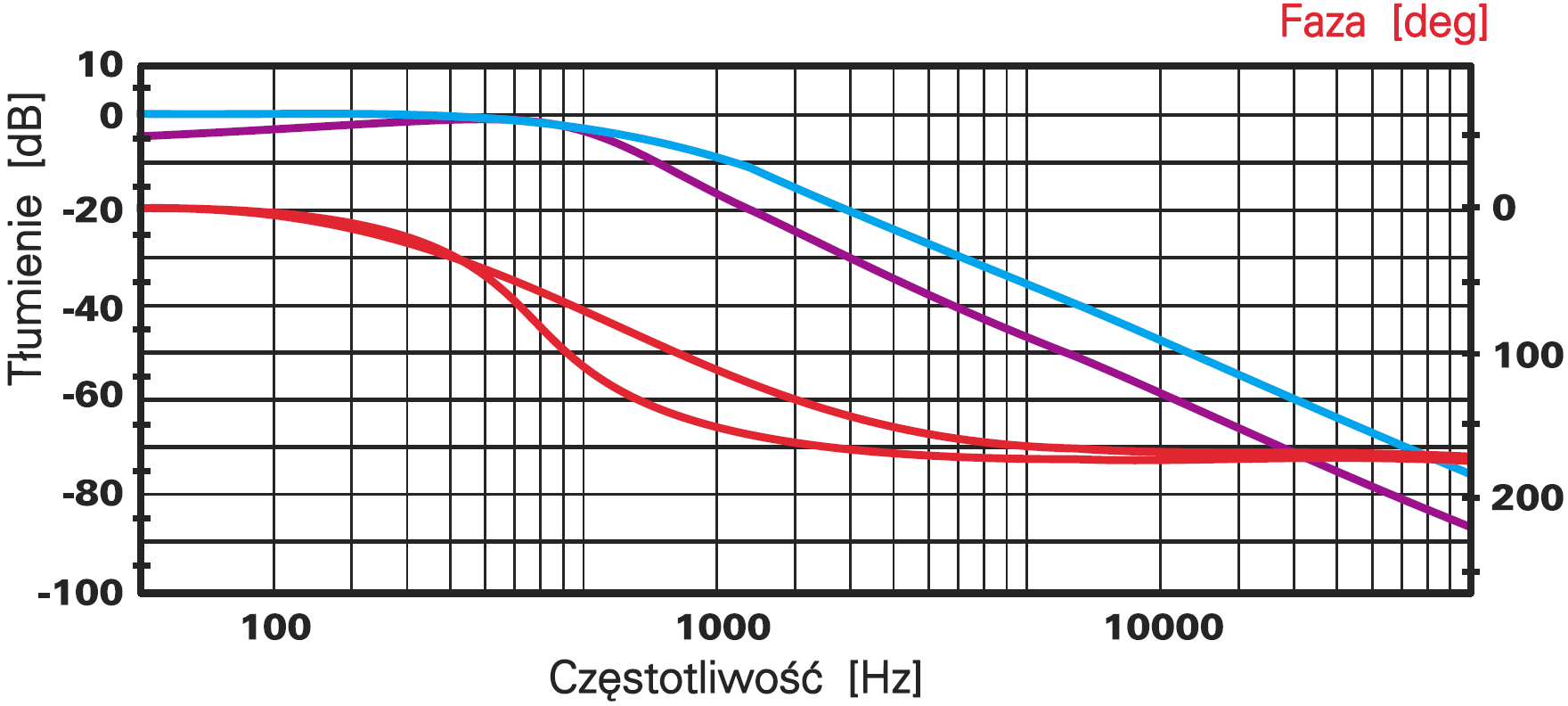
Profesjonaliści w niektórych przypadkach muszą uwzględnić, jaka jest faza poszczególnych składowych, które przechodzą przez filtr. Dlatego często podaje się też charakterystykę fazową filtru. Na rysunku 1 pokazane są charakterystyki amplitudowa i fazowa dwóch filtrów dolnoprzepustowych drugiego rzędu. Niebieskie krzywe to charakterystyki amplitudowe, czerwone – fazowe.

W niektórych przypadkach bardzo istotne jest, jakie właściwości ma filtr w paśmie zaporowym. W innych zastosowaniach kluczowe znaczenie ma sposób, w jaki filtr reaguje na kilka impulsów o określonej częstotliwości lub jak odpowiada na specyficzne sygnały, jak choćby impuls prostokątny. W takich wypadkach obok charakterystyki fazowej istotny jest pokrewny parametr − opóźnienie grupowe.

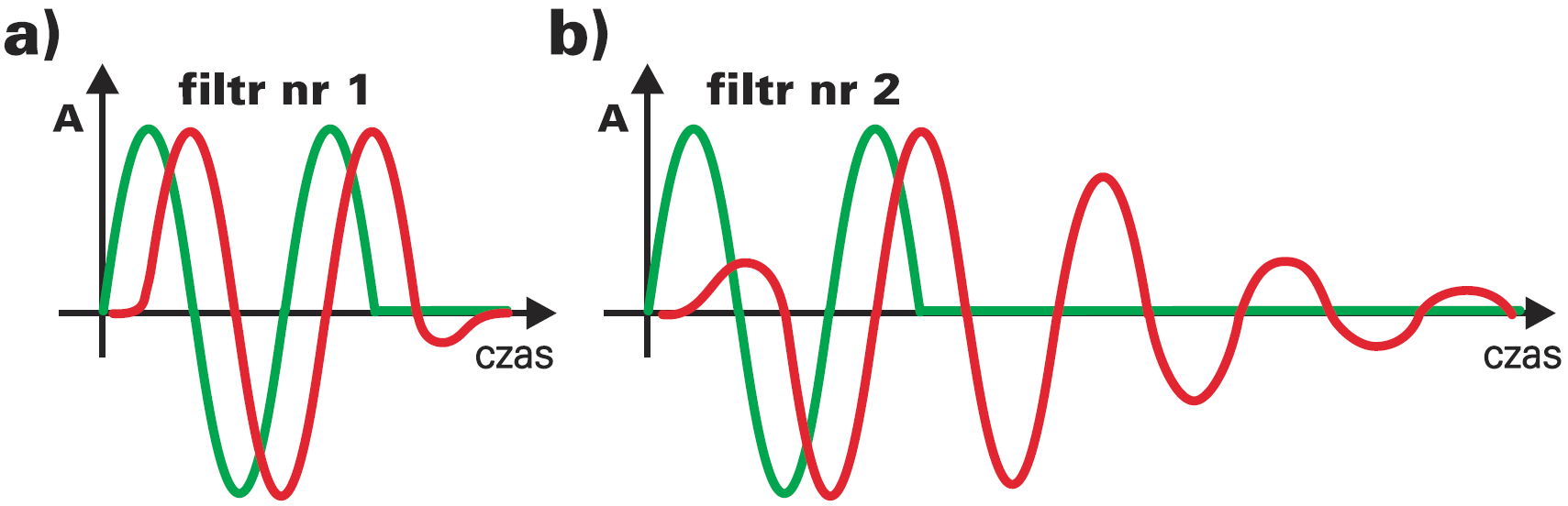
Charakterystyka częstotliwościowa nic nie mówi na przykład o odpowiedzi na ciąg impulsów. Czy po zakończeniu ciągu impulsów sygnał na wyjściu filtru zaniknie od razu, czy drgania będą gasnąć powoli. Rysunek 2 pokazuje odpowiedź dwóch filtrów na paczkę impulsów. Kolorem zielonym narysowałem przebieg wejściowy, kolorem czerwonym – wyjściowy. Od razu widać, że w filtrze nr 2 oscylacje na wyjściu zanikają wolniej – mówimy, że ten filtr ma większą skłonność do „dzwonienia”.

A oto kolejny parametr, o którym warto wiedzieć. Amatorzy zupełnie nie zwracają uwagi na parametry filtru zwane wrażliwością. Parametry te wskazują między innymi, jak zmieniają się właściwości filtru przy zmianie wartości elementów. Może Ci się to wydać dziwne, że na przykład w jednym filtrze zmiana pojemności kondensatora o 5% zaowocuje zmianą częstotliwości granicznej też o 5%, a w innym tylko o 3%. Oczywiście lepszy jest ten drugi, mniej wrażliwy na nieuniknione rozrzuty wartości elementów.

Jeszcze raz powtarzam: na razie nie musisz się przejmować tymi dodatkowymi parametrami. W zdecydowanej większości przypadków będziesz się interesować jedynie charakterystyką amplitudową, a niekiedy też skłonnością do „dzwonienia“.

Rodzaje filtrów

Już rysunek 6 w poprzednim odcinku pokazał, że filtr o potrzebnej charakterystyce można zrealizować na różne sposoby, czyli według różnych schematów. Istnieje mnóstwo rodzajów i odmian rozwiązań układowych, niektóre o wręcz porażających nazwach. Oto przykładowe nazwy filtrów: Sallen−Keya, ze źródłem napięciowym sterowanym napięciowo, INIC, z wielokrotnym sprzężeniem zwrotnym, filtry zmiennych stanu, filtry uniwersalne, filtry bikwadratowe, itd.

Teoretycy oraz specjaliści w specyficznych dziedzinach wymyślili i wciąż wymyślają kolejne rozwiązania układowe. Oprócz klasycznych filtrów z elementami RC wykorzystuje się tak zwane filtry z przełączanymi pojemnościami. Ostatnio, ze względu na lawinową ekspansję techniki cyfrowej, filtry realizuje się programowo, a filtrowanie polega na przetwarzaniu strumienia informacji.

My w ramach niniejszego cyklu artykułów zajmiemy się głównie dwoma klasycznymi i wciąż popularnymi rodzajami filtrów. Są to:
− filtry z wielokrotnym sprzężeniem zwrotnym
− filtry ze sterowanym źródłem napięciowym, zwane filtrami Sallen−Keya.

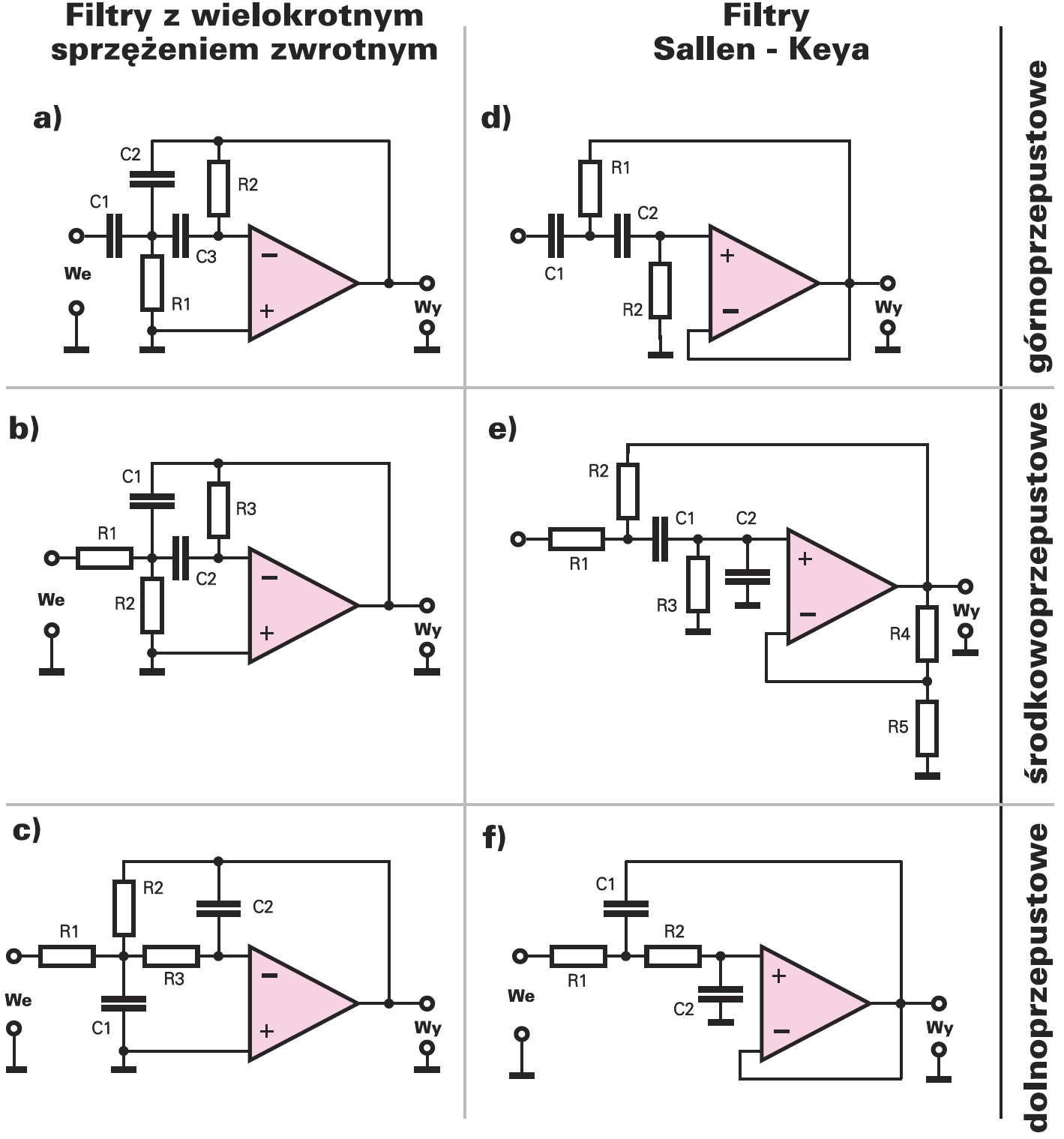
Podstawowe ogniwa tych filtrów (filtry drugiego rzędu) znajdziesz na rysunku 3.

Zwróć uwagę na podobieństwa – charakterystyka zależy od rozmieszczenia rezystorów i kondensatorów.

Rodzaj charakterystyki

Pora teraz wyraźnie rozdzielić dwa zupełnie różne zagadnienia. W poprzedzającym fragmencie wymieniłem kilka bardziej popularnych nazw rozwiązań układowych. Każde takie rozwiązanie pozwala zrealizować filtr dolnoprzepustowy, górnoprzepustowy i środkowoprzepustowy. Podana nazwa wskazywała, według jakiego schematu zrealizowany jest filtr. Nazwa ta nie mówi jednak nic o szczegółach przebiegu charakterystyki.

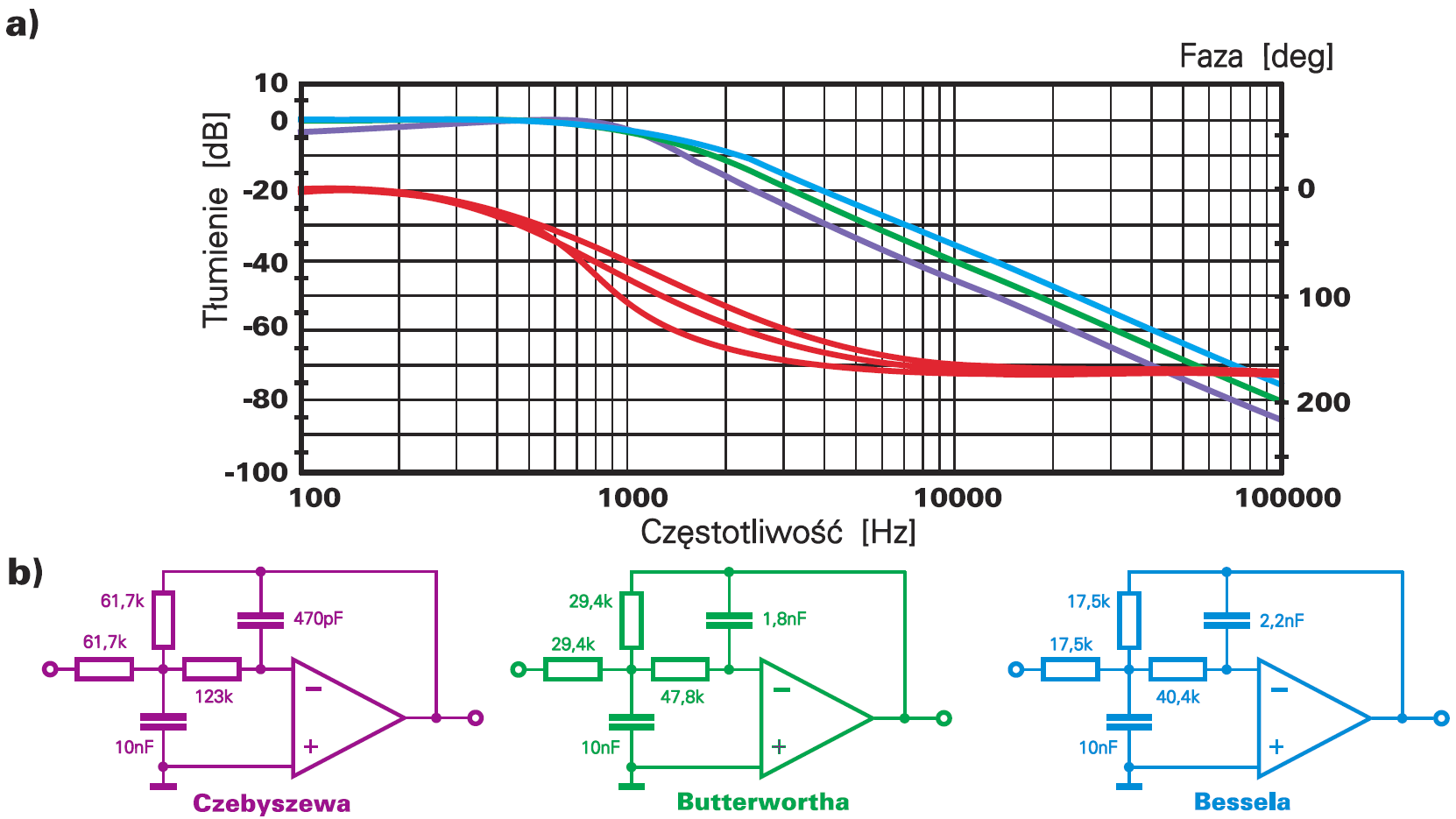
Natomiast określenia: filtr Butterwortha, Czebyszewa, Cauera, Bessela, Thomsona czy filtr eliptyczny nie mówią nic o fizycznej realizacji, czyli o schemacie, tylko o najważniejszych właściwościach (charakterystykach amplitudowej, fazowej, opóźnienia grupowego, itp.). Rysunek 4a pokazuje trzy charakterystyki filtru dolnoprzepustowego drugiego rzędu o schemacie z rysunku 3c i częstotliwości granicznej 1 kHz. Czerwone linie to charakterystyki fazowe (które teraz nas niewiele interesują). Niebieskim kolorem zaznaczyłem filtr i charakterystykę Bessela. Kolorem zielonym − Butterwortha, a kolorem fioletowym – Czebyszewa. Zauważ, że odmienny przebieg charakterystyk uzyskujemy w tym samym układzie przy różnych wartościach elementów RC – porównaj rysunek 4b, gdzie wartość kondensatora C1 we wszystkich przypadkach wynosi 10 nF.

 

W filtrze (o charakterystyce) Czebyszewa uzyskujemy najlepsze tłumienie w paśmie przejściowym, tuż powyżej częstotliwości granicznej. Niestety, filtr ten ma najgorszą charakterystykę fazową, opóźnieniową, a do tego zafalowania w paśmie przepustowym. Dlatego przy omawianiu i projektowaniu filtrów (o charakterystyce) Czebyszewa oprócz częstotliwości granicznej podaje się też zafalowania w paśmie przepustowym (wyrażane w decybelach). W praktycznych układach dopuszcza się falistość charakterystyki co najwyżej 3 dB. Inaczej jest z filtrem Bessela (kolor niebieski). Nie ma żadnych zafalowań w charakterystyce amplitudowej. Faza i opóźnienie grupowe są najlepsze, ale za to charakterystyka amplitudowa – najmniej stroma.

Zaznaczona na zielono charakterystyka Butterwortha jest, można powiedzieć, kompromisowa. Filtr Butterwortha jest w pewnym sensie filtrem „średnim“: przebieg charakterystyki amplitudowej w paśmie przepustowym aż do częstotliwości granicznej jest maksymalnie płaski, stromość powyżej częstotliwości granicznej i inne parametry – niezłe.

Filtry (o charakterystyce) Butterwortha są wykorzystywane bardzo często. Filtry Bessela – rzadko, głównie w układach impulsowych, gdzie istotna jest faza i kształt impulsu na wyjściu. Filtry (o charakterystyce) Czebyszewa są stosowane tam, gdzie najważniejsze są ostre zbocza charakterystyki amplitudowej.

Zwróć uwagę, że filtr Czebyszewa zapewnia tłumienie nieco lepsze od innych, ale różnica nie jest duża, co najwyżej kilkanaście decybeli – nachylenie charakterystyki dla częstotliwości znacznie większych od granicznej jest takie samo, jak w filtrach Butterwortha i Bessela. Potwierdza się wniosek, że aby uzyskać zdecydowanie większą stromość, trzeba zastosować filtr wyższego rzędu, zawierający kilka ogniw.

Na marginesie dodam, że rysunki 3, 7, 8 pokazują charakterystyki filtrów Butterwortha, a rysunek 5, jak wspomniałem – Czebyszewa o falistości 2 dB (wszystkie rysunki są zaprezentowane w poprzedniej części). Porównując rysunek 5 w poprzedniej części z fioletową krzywą z rysunku 4a zwróć uwagę, że czym wyższy rząd filtru Czebyszewa, tym więcej zafalowań w paśmie przepustowym.

Tak samo jest z filtrami górnoprzepustowymi, nieco inaczej ze środkowoprzepustowymi.

Przypominam, że te charakterystyki Bessela, Butterwortha i Czebyszewa można osiągnąć w tym samym układzie elektrycznym, odpowiednio dobierając wartości elementów RC.

I tyle w tym odcinku. W następnym odcinku nadal będziemy zajmować się kolejnymi ważnymi zagadnieniami ogólnymi, a potem zaczniemy wreszcie projektować filtry.

Piotr Górecki