Filtry aktywne – część 5
W poprzednim odcinku podałem kilka istotnych informacji na temat elementów jakie powinno się stosować przy budowie filtrów aktywnych. W dwóch najbliższych odcinkach zajmiemy się odmianami filtrów górnoprzepustowych i wspólnie zaprojektujemy kilka filtrów. Wszystkie omawiane układy są filtrami drugiego rzędu, więc stromość charakterystyki wynosi 12 dB/oktawę (40 dB/dekadę).
Na początku każdego odcinka umieściłem gotowe proste recepty dla niecierpliwych praktyków. Skorzystanie z nich jest beznadziejnie łatwe. Przekonują o tym zaprezentowane przykłady rachunkowe. W dalszej części każdego odcinka bardziej zaawansowani znajdą ogólne wzory, nieco bardziej skomplikowane, ale za to pozwalające dobrać dodatkowe parametry.
Aby w pełni skorzystać z podanego materiału, konieczne jest przyswojenie sobie informacji ze wszystkich odcinków wstępnych, począwszy od pierwszego artykułu cyklu.
Filtr górnoprzepustowy z wielokrotnym sprzężeniem zwrotnym
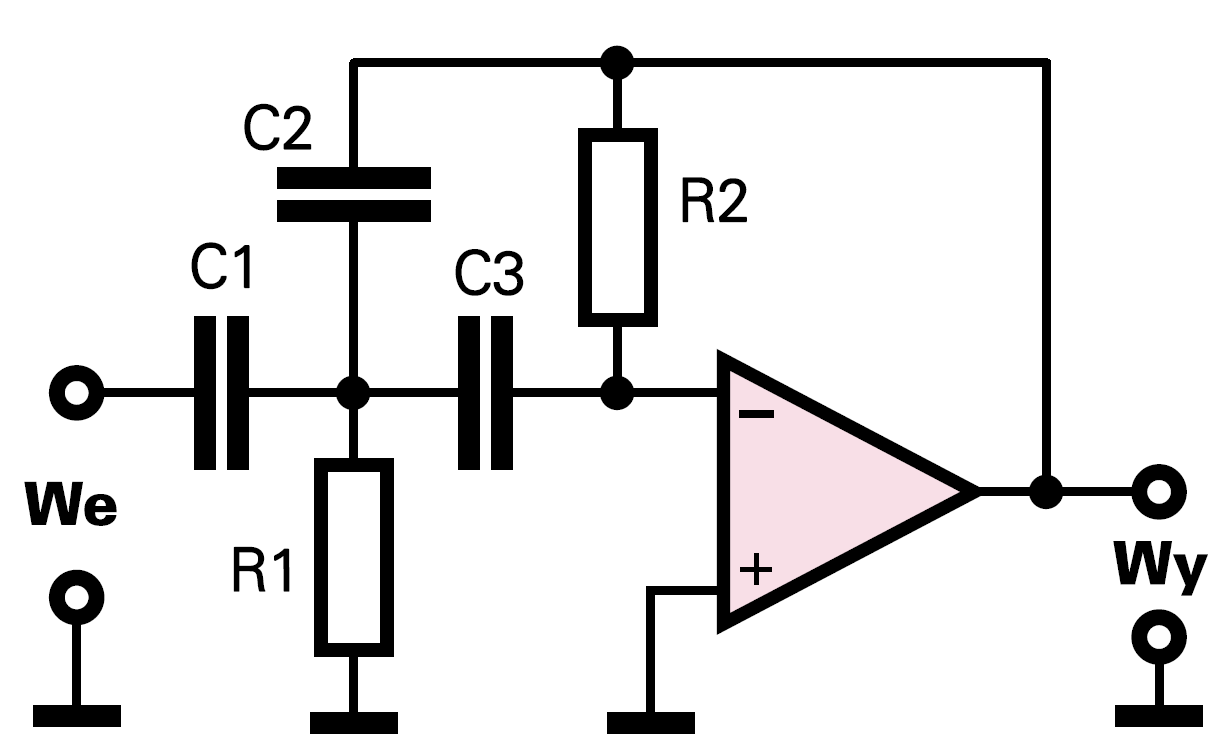
Najpierw bierzemy na warsztat filtr z wielokrotnym sprzężeniem zwrotnym (MFB − multiple feedback). Schemat ideowy pokazany jest na rysunku 1.
Aby zmieścić się w zalecanym zakresie wartości elementów posłużymy się wzorem:
C [nF] = 10000 [nFHz] / f [Hz]
Pojemność wychodzi w nanofaradach, jeśli częstotliwość podamy w hercach. Jeżeli obliczona wartość nie jest „okrągła”, wybierz najbliższą wartość z szeregu E6 (1; 1,5; 2,2; 3,3; 4,7; 6,8).
Przy wzmocnieniu równym 1 wszystkie kondensatory będą jednakowe:
C=C1=C2=C3
Następnie obliczamy reaktancję wybranego kondensatora przy częstotliwości granicznej:
![]()
Uwaga! Podstawiasz tu wybraną wartość pojemności z szeregu E6, a nie wartość obliczoną wcześniej ze wzoru! Reaktancja wychodzi w kiloomach, jeśli częstotliwość podamy w hercach, a pojemność w nanofaradach.
Następnie obliczamy wartości rezystorów w zależności od dobroci filtru, którą chcemy uzyskać:
Dla dobroci 0,5:
R1 = Xc × 1 R2 = Xc × 2,25
Dla dobroci 0,707:
R1 = Xc × 0,472 R2 = Xc × 2,12
Dla dobroci 1,35 (podbicie +3 dB):
R1 = Xc × 0,178 R2 = Xc × 2,86
Rysunek 2 pokazuje charakterystyki filtrów o częstotliwości granicznej 1 kHz, obliczonych według podanych właśnie wzorów z rezystorami o dokładnych wartościach obliczonych ze wzoru. We wszystkich przypadkach pojemność wynosi 10 nF, natomiast wartości rezystorów wynoszą:
Q=0,5: R1=15,9 kΩ, R2=35,8 kΩ
Q=0,7: R1=7,50 kΩ, R2=33,7 kΩ
Q=1,35: R1=2,83 kΩ, R2=45,5 kΩ
Kto chce, może żmudnie dobierać rezystory, jeśli koniecznie chce uzyskać dokładne wartości wyliczone ze wzorów, ale nie ma to żadnego sensu, jeśli zastosowane kondensatory mają tolerancję 10% lub 5%. Należy po prostu wziąć najbliższe nominały z szeregu 1−procentowego, albo jeśli ktoś nie ma takich możliwości, nawet z szeregu 5−procentowego. Drobne różnice wartości uzyskanej częstotliwości granicznej rzędu kilku procent w większości przypadków nie mają żadnego znaczenia.
Przykłady
Żeby utrwalić podane informacje, zaprojektujmy wspólnie filtr górnoprzepustowy o częstotliwości granicznej, powiedzmy, 80 Hz i dobroci 0,707. Można go zastosować w torze mikrofonowym do odcięcia najniższych składowych. Taki filtr często spotyka się w profesjonalnych konsolach mikserskich jako tak zwany filtr kroków.
Najpierw dobieramy pojemność:
C [nF] = 10000 [nFHz] / 80 [Hz] = 125 nF
W szeregu E6 mamy najbliższe pojemności 100 nF i 150 nF. Decydujemy się na 100 nF (foliowy MKT). Wszystkie kondensatory będą jednakowe:
C=C1=C2=C3
Reaktancja przy częstotliwości granicznej wynosi:
Xc [kΩ] = 160000 / (80 [Hz] × 100 [nF]) Xc = 20 kΩ
Obliczamy wartości rezystorów dla dobroci filtru równej 0,707:
R1 = 20 kΩ × 0,472 = 9,44 kΩ R2 = 20 kΩ × 2,12 = 42,4 kΩ
Filtr nie musi być precyzyjny, więc zastosujemy rezystory z szeregu 5−procentowego:
R1 = 9,1kΩ R2 = 43 kΩ
Schemat i charakterystyki filtru pokazane są na rysunku 3a,b. Linią czerwoną zaznaczono charakterystykę z rezystorami z szeregu 5−procentowego. 3−decybelowa częstotliwość graniczna wynosi 78,7 Hz, a różnica o niecałe 1,3 Hz w stosunku do założonej jest zupełnie nieistotna.
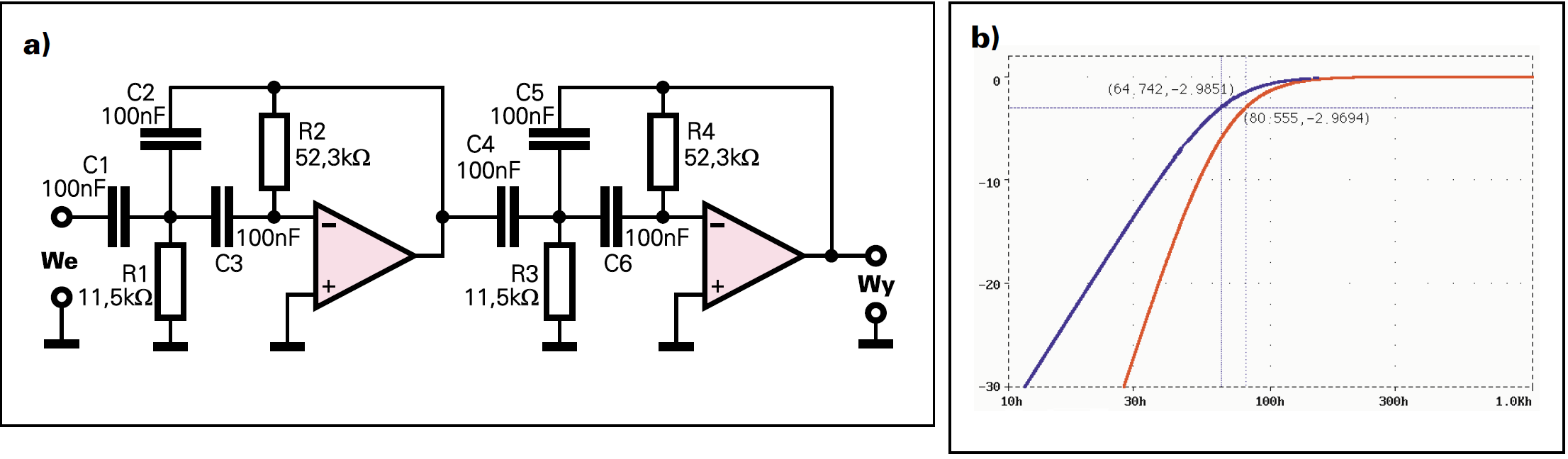
Rozpatrzmy podobny filtr o większej stromości. W filtrze kroków większa stromość nie jest potrzebna, ale jeśli filtr miałby jednocześnie likwidować brum 50 Hz, można rozważyć taką możliwość. Połączenie dwóch jednakowych filtrów z rysunku 3 da filtr o stromości 80 dB/dekadę, ale 3−decybelowa częstotliwość graniczna nieuchronnie przesunie się w górę do około 97 Hz. Aby ją obniżyć trzeba zwiększyć rezystancję mniej więcej 1,2− krotnie. Rysunek 4a,b pokazuje schemat i charakterystyki filtru z tak skorygowanymi wartościami rezystorów z 1−procentowego szeregu E96: 11,5 kΩ, 52,3 kΩ.
Czerwoną linią zaznaczono charakterystykę wypadkową o częstotliwości granicznej 80,55 Hz. Linia niebieska pokazuje charakterystykę jednego filtru, który jak widać, ma częstotliwość graniczną około 64 Hz.
Dla zaawansowanych i dociekliwych
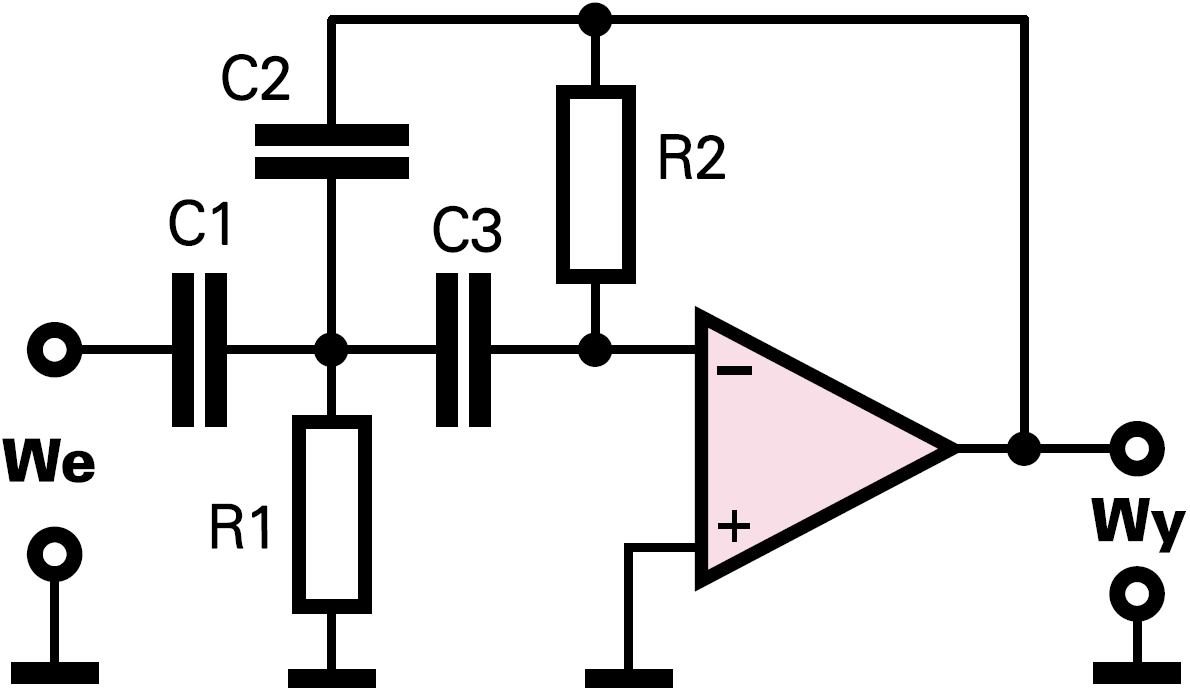
Podane sposoby obliczania filtru drugiego rzędu są bardzo proste i przyjazne, niemniej nie pozwalają w pełni wykorzystać możliwości danej konfiguracji. Jeśli ktoś chce, może skorzystać z nieco bardziej skomplikowanej procedury projektowej. Nadal rozważamy układ filtru MFB powtórzony na rysunku 5.
Tym razem znajdziemy wartości elementów dla dowolnych wartości częstotliwości, dobroci i co jest nowością – wzmocnienia. Do obliczeń potrzebujemy wartości:
fo – częstotliwości granicznej
Q – dobroci
G – wzmocnienia.
Obliczenia
Na początek dla ułatwienia przyjmujemy, że C1=C3 i wybieramy wartość:
C [nF] = 10000 [nFHz] / f [Hz]
Pojemność wychodzi w nanofaradach, jeśli częstotliwość podamy w hercach. Wybieramy najbliższą wartość z szeregu.
Mamy już C1=C3=C
Obliczamy reaktancję wybranego kondensatora przy częstotliwości granicznej:
![]()
podstawiając wybraną wartość pojemności z szeregu, a nie wartość obliczoną wcześniej ze wzoru. Reaktancja wychodzi w kiloomach, jeśli częstotliwość podamy w hercach, a pojemność w nanofaradach.
Teraz obliczamy wartości pozostałych elementów w zależności od dobroci filtru i wzmocnienia:
![]()
Wybierana na początku procedury projektowej wartość pojemności C może być praktycznie dowolna (wtedy inne będą też wartości innych elementów). Przy podanym sposobie obliczania pozostałe elementy też będą mieć „rozsądne” wartości. Nie należy bez potrzeby zwiększać pojemności, bo wejście filtru będzie stanowić niepotrzebnie duże obciążenie pojemnościowe dla poprzedniego stopnia – kondensator C1 jest w istocie dołączony do punktu wirtualnej masy. Przy doborze wzmocnienia G i dobroci Q należy się kierować wskazówkami podanymi we wstępnych odcinkach cyklu.
A w kolejnym odcinku będziemy kontynuować nadal temat dotyczący filtrów górnoprzepustowych.
Piotr Górecki