Elektronika (nie tylko) dla informatyków (6) Kondensator – śladami Fouriera

W ostatnim wykładzie przeanalizowaliśmy podstawowe właściwości kondensatora i doszliśmy do wniosku, że miałoby sens mówienie o oporności kondensatora, ale tylko w przypadku sinusoidalnych przebiegów napięcia i prądu.

Do tego ważnego wątku jeszcze wrócimy, ale postanowiłem, że najpierw zasygnalizuję Ci kilka bardzo ważnych, fundamentalnych zagadnień. Dopiero wyposażony w taką wiedzę powrócisz do właściwości kondensatorów i innych związanych z nimi zagadnień praktycznych.

Najprostszy przebieg

Zwyczajny kondensator i nasze proste dociekania z poprzedniego odcinka pokazały bardzo ważną tajemnicę: przebieg sinusoidalny ma wyjątkowe właściwości. Otóż jeśli przebieg napięcia na kondensatorze ma kształt sinusoidalny, to przebieg prądu też będzie miał kształt sinusoidalny. I oczywiście na odwrót. Natomiast przy każdym innym kształcie – przebiegi napięcia i prądu nie będą mieć tej samej formy – porównaj rysunki 4…7 z poprzedniego odcinka.

Przyjmij do wiadomości, że w związku z takimi właściwościami, przebieg sinusoidalny możemy nazwać przebiegiem elementarnym, podstawowym albo najprostszym. Tak! Najprostszym!

Może tu się sprzeciwisz i powiesz, że prostszymi przebiegami są przebiegi prostokątny i trójkątny. Takie odczucie mogą mieć też elektronicy – praktycy. Wiedzą oni, że wytworzenie przebiegu prostokątnego jest dziecinnie proste, trójkątnego – trochę trudniejsze, a wytworzenie „czystego” przebiegu sinusoidalnego to naprawdę niełatwe zadanie. I teraz miałoby się okazać, że najprostszym przebiegiem jest sinusoidalny?

Otóż tak! To właśnie sinusoida jest podstawowym, elementarnym przebiegiem! Nie będziemy wgłębiać się we wszystkie szczegóły i w matematykę wyższą. Warto jednak, żebyś jak najwcześniej oswoił się z pewnymi informacjami, które z początku nie wydają się zgodne z intuicją.

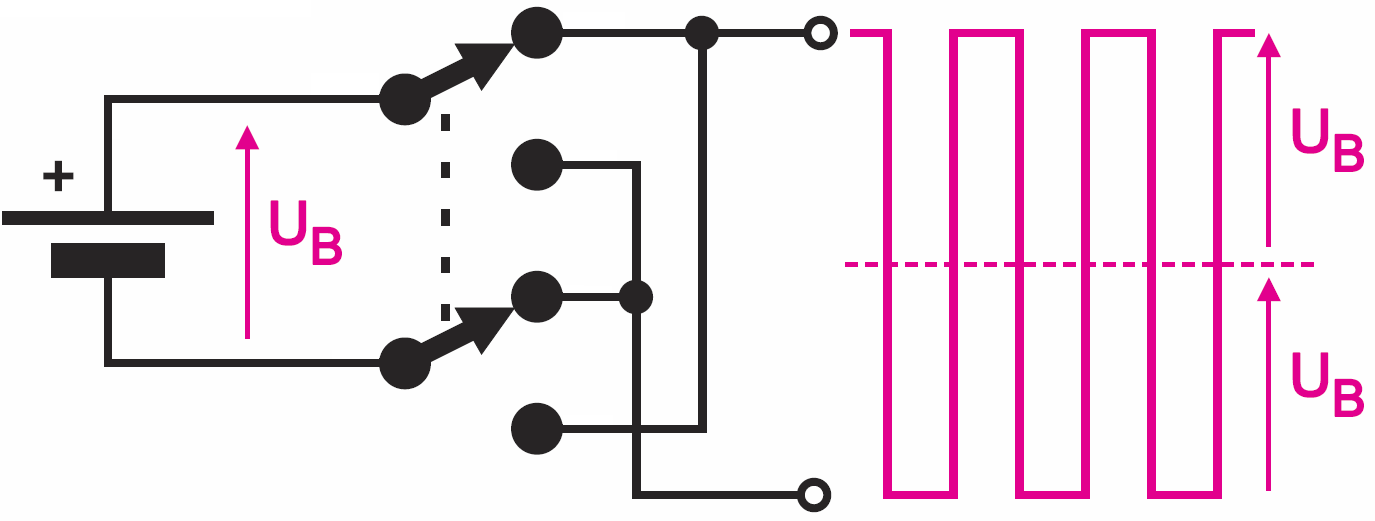
Otóż początkującym wydaje się, że „prosty” jest przebieg prostokątny, który istotnie można wytworzyć w prosty sposób, choćby za pomocą przełącznika według idei z rysunku 1.

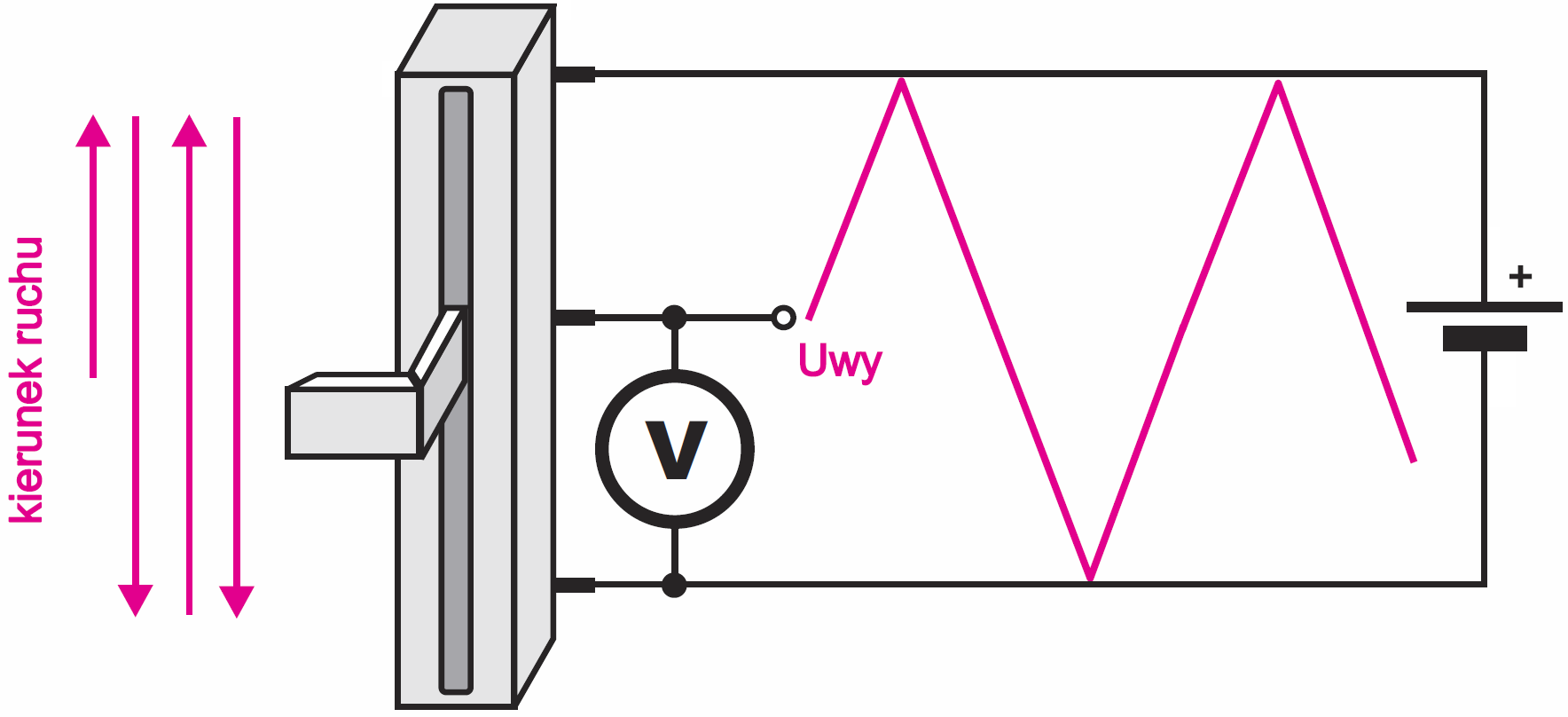
Intuicyjnie prosty wydaje się też sposób wytwarzania przebiegu trójkątnego, czyli takiego, w którym zbocza mają stałe, jednakowe nachylenie. Trójkątny przebieg napięcia można byłoby wytwarzać, przesuwając suwak potencjometru ruchem jednostajnym tam i z powrotem, na przykład według idei z rysunku 2. Proste, prawda?

A skąd wziąć przebieg sinusoidalny?
Problem nie jest tak wielki, jak mogłoby się wydawać! Zapomnij jednak na chwilę o wszystkim, co wiesz na temat generatorów „sinusoidy”, bo to tylko zaciemnia sprawy najważniejsze. A oto bardzo ważne pytanie:

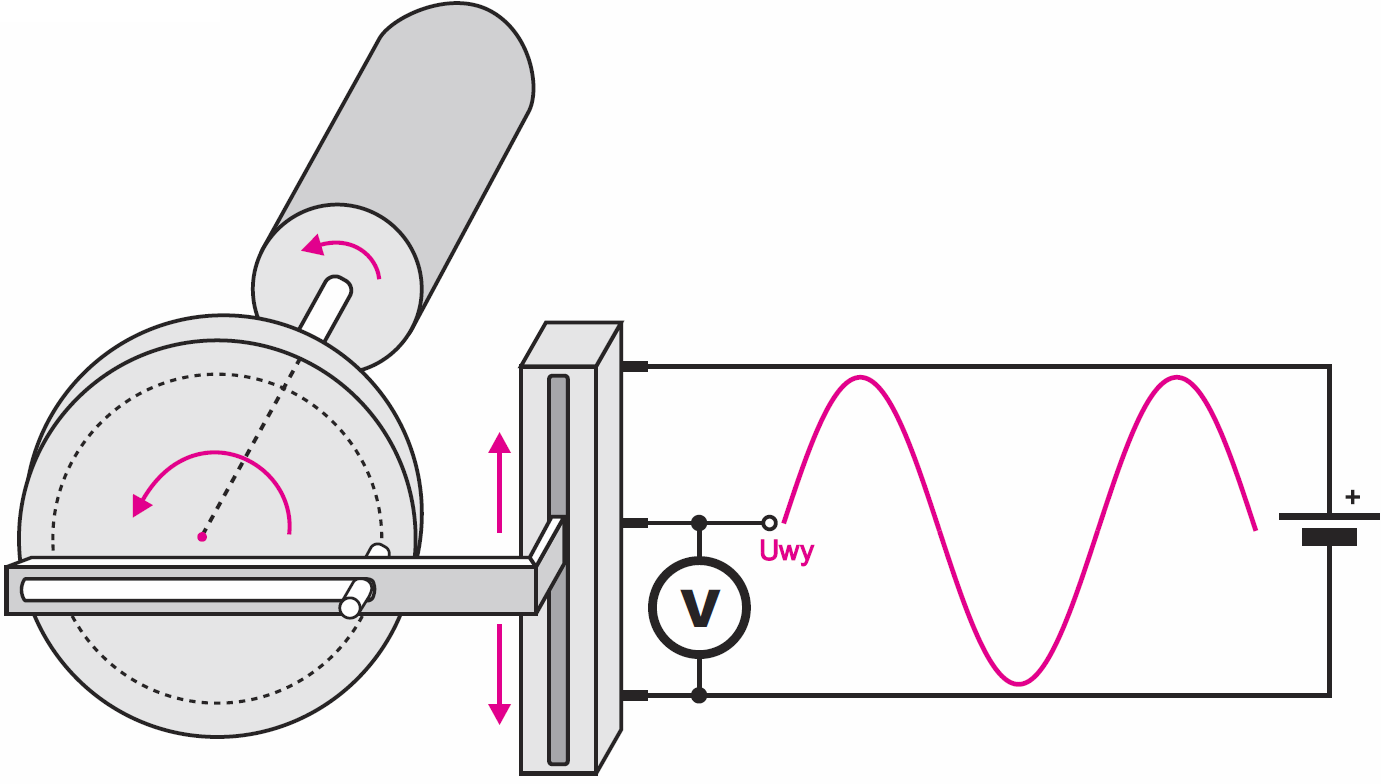
Czy masz świadomość, że sinusoida jest nierozłącznie związana z ruchem obrotowym? Nie?

Otóż sinusoida naprawdę jest ściśle powiązana z ruchem obrotowym. Choć przebiegi sinusoidalne można otrzymywać na wiele sposobów, kluczowym dla zrozumienia wielu ważnych zagadnień elektroniki są metody związane z wykorzystaniem ruchu obrotowego. Przeanalizuj dokładnie rysunek 3 pokazujący, w jaki sposób można byłoby uzyskiwać przebieg sinusoidalny za pomocą potencjometru suwakowego i obracającej się tarczy z bolcem i jarzmem. Jeśli w takim mechanizmie nie byłoby żadnych luzów, to napięcie z suwaka potencjometru miałoby doskonały kształt sinusoidalny. Być może widziałeś już wcześniej nieco podobny rysunek na lekcji matematyki, gdy nauczyciel omawiał funkcję sinus. Tak, funkcja matematyczna sinus ma ścisły związek z ruchem obrotowym.

Oczywiście w praktyce do wytwarzania przebiegu sinusoidalnego nie wykorzystujemy silnika, tarczy z bolcem i zmodyfikowanego potencjometru suwakowego. Ale podstawową zasadę wiążącą ruch obrotowy z przebiegiem sinusoidalnym powszechnie wykorzystujemy w różnego typu generatorach – prądnicach. W ten sposób wytwarzane jest napięcie, które mamy w sieci energetycznej. Fotografia 4 przedstawia zespół turbina + generator prądotwórczy o mocy 10,5 MW (10500000 W) w lubelskiej elektrociepłowni Megatem (www.megatem-ec.pl). Potężne generatory wirują z prędkością 3000 obr/min, czyli 50 obrotów na sekundę.

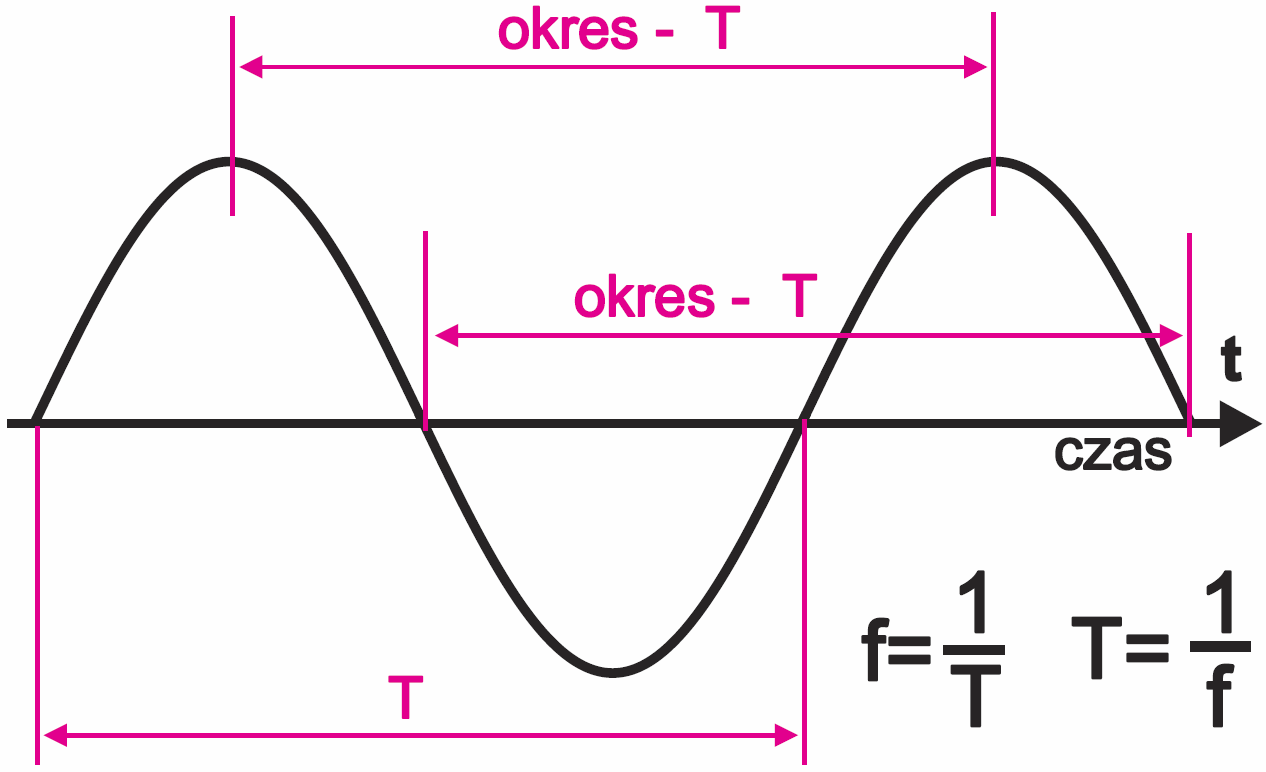
Nietrudno się domyślić, że generatory takie wytwarzają przebieg sinusoidalny, zawierający w ciągu sekundy 50 pełnych cykli, czyli okresów. Mówimy, że jego częstotliwość wynosi 50 herców (50 Hz). Jeden okres takiego przebiegu trwa 1/50 sekundy, czyli 20 milisekund.

Częstotliwość oznaczamy literą F lub f, od angielskiego frequency i wyrażamy w hercach, czyli drganiach na sekundę (także w kilohercach kHz, megahercach MHz i gigahercach GHz). Nazwa jednostki częstotliwości, herc, pochodzi od nazwiska XIX wiecznego niemieckiego fizyka Heinricha Rudolfa Hertza, który położył podwaliny pod rozwój radiokomunikacji.

Okres zwykle oznaczamy literą T i wyrażamy w jednostkach czasu: sekundach, milisekundach, mikrosekundach lub nanosekundach.

Jak też pokazuje rysunek 5, okres i częstotliwość są nierozerwalnie związane zależnościami:                  f = 1 / T        T = 1/ f

W praktyce przy obliczeniach trzeba pamiętać o prawidłowych jednostkach (warto pamiętać, że przy obliczaniu odwrotności: 1/f i 1/T jednostki występują parami: herc-sekunda, kiloherc-milisekunda, megaherc-mikrosekunda). W elektronicznej praktyce mamy do czynienia przede wszystkim z przebiegami napięcia i prądu o częstotliwościach od pojedynczych herców do wielu megaherców, czyli takimi, których okres wynosi od sekundy do ułamków mikrosekund.

W wielu podręcznikach podstaw elektroniki nie wiąże się przebiegu sinusoidalnego z ruchem obrotowym. W efekcie młodzi elektronicy mają kłopot ze zrozumieniem pewnych ważnych zagadnień, w tym wykresów wskazowych i miary kątowej. Tymczasem właśnie powiązanie sinusoidy z ruchem obrotowym znakomicie ułatwia zrozumienie i przyswojenie tych ważnych zagadnień. Zanim się jednak tym zajmiemy, muszę Ci pokazać, choć w ogólnym zarysie, zasygnalizowaną już bardzo ważną sprawę „prostych” i „nieprostych” przebiegów.

Nie taki Fourier straszny…

Nawet jeśli boisz się wgłębiać w szczegóły, czemu się zresztą nie dziwię, wbij sobie do głowy informację, że przebieg sinusoidalny jest podstawowym, najprostszym przebiegiem. Natomiast przebiegi o wszelkich innych kształtach są w istocie złożeniem (najczęściej bardzo) wielu przebiegów sinusoidalnych.

Być może słyszałeś o czymś takim jak transformata Fouriera czy szereg Fouriera. Nie bój się. Choć ze strony matematycznej są to trudne zagadnienia, to jednak podstawowa zasada jest prosta:

każdy przebieg okresowy o dowolnym kształcie i częstotliwości f jest w istocie złożeniem (najczęściej wielu) przebiegów sinusoidalnych o częstotliwościach będących całkowitymi wielokrotnościami częstotliwości podstawowej f.

Te częstotliwości składowe nazywamy częstotliwościami harmonicznymi. Przykładowo dla przebiegu o częstotliwości f = 1 kHz, druga harmoniczna ma częstotliwość 2kHz (co często zapisujemy f₂ = 2 kHz), trzecia: 3 kHz, czwarta: 4 kHz i tak dalej. Od razu warto dodać, że można mówić też o zerowej harmonicznej (f₀) – to składowa stała.

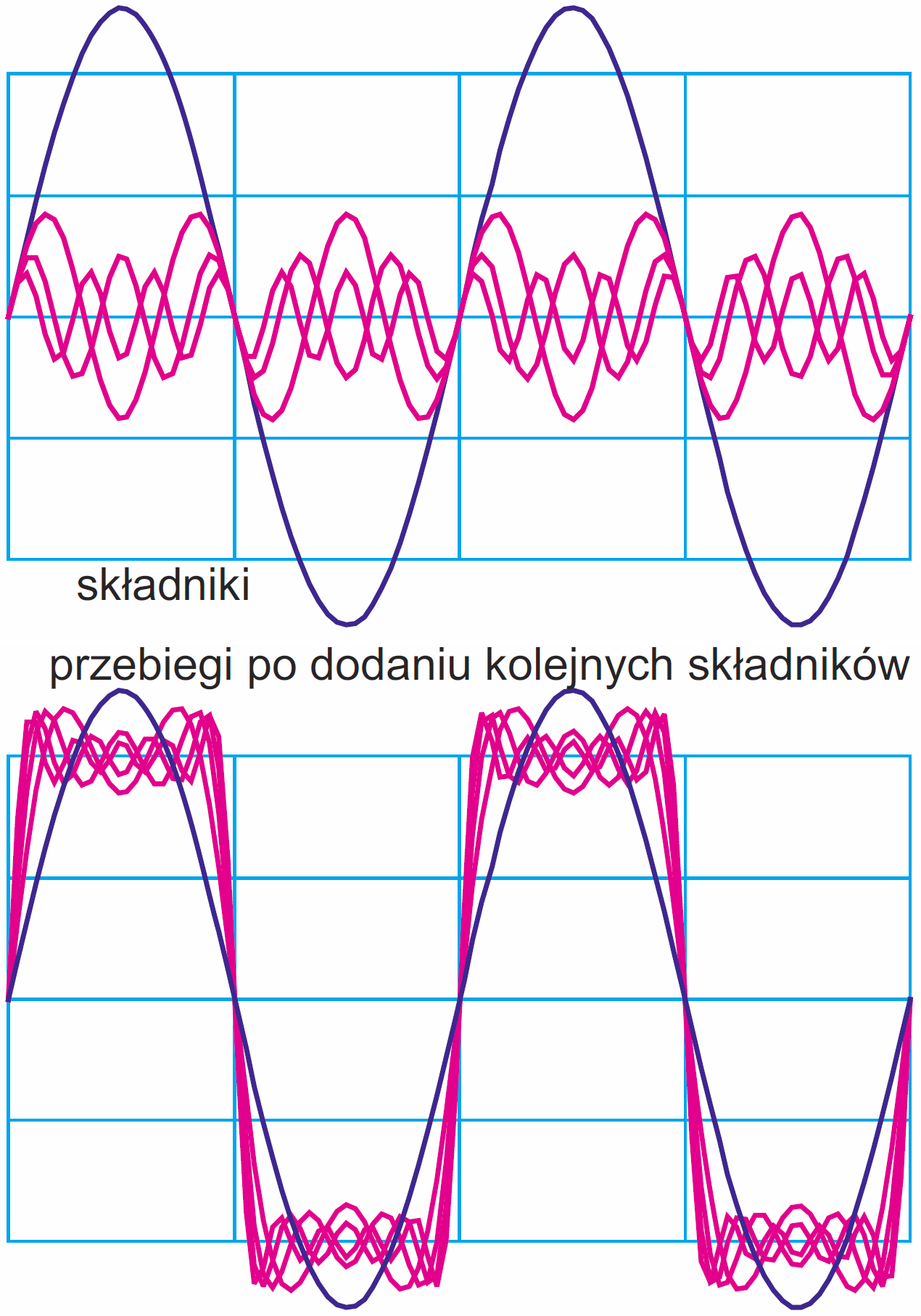
Można więc przebieg o dowolnym kształcie złożyć z odpowiedniej liczby przebiegów harmonicznych. Ilustruje to w uproszczeniu rysunek 6, gdzie w górnej części pokazane są składniki, a w dolnej wygląd przebiegu przy dodawaniu kolejnych składników. Zauważ, że dodanie kolejnego składnika zniekształca pierwotny, czysty przebieg sinusoidalny – dlatego też mówimy o zniekształceniach harmonicznych, które traktujemy jako coś złego.

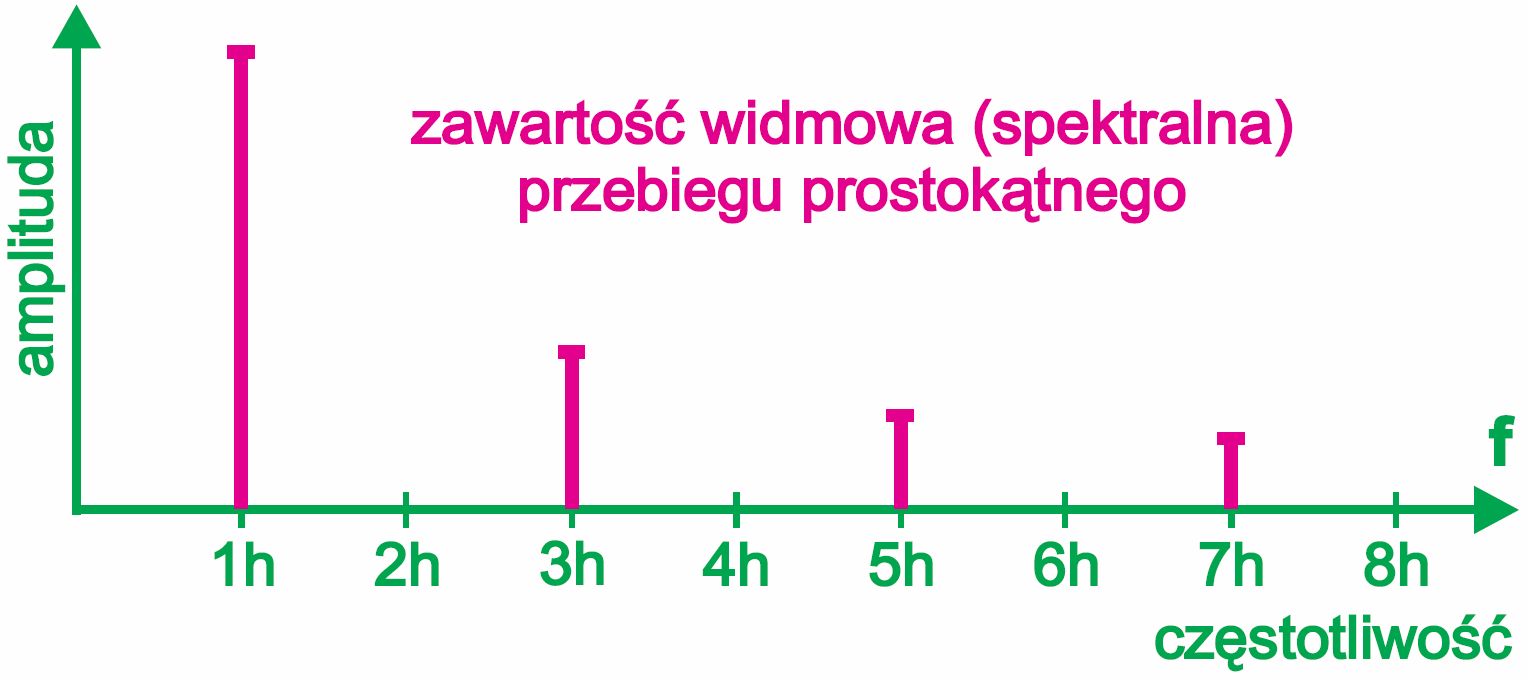
Ale można spojrzeć na to inaczej: jak widać, odpowiednio dobrana kolejna harmoniczna coś dodaje, coś odejmuje i przebieg stopniowo upodabnia się do prostokąta. Idealny przebieg prostokątny musiałby zawierać nieskończoną liczbę nieparzystych harmonicznych o odpowiednio dobranej wielkości. Warto dodać, że w przypadku przebiegu prostokątnego tymi składnikami są tylko harmoniczne nieparzyste: trzecia, piąta, siódma, … Oczywiście muszą mieć one odpowiednio dobraną wielkość. Podobnie przebieg trójkątny też jest zbudowany z odpowiednio dobranych nieparzystych harmonicznych, ale inaczej dobranych. Jest to ściśle opisane matematycznie, na przykład „przepis” na przebieg prostokątny zawiera poniższy wzór:

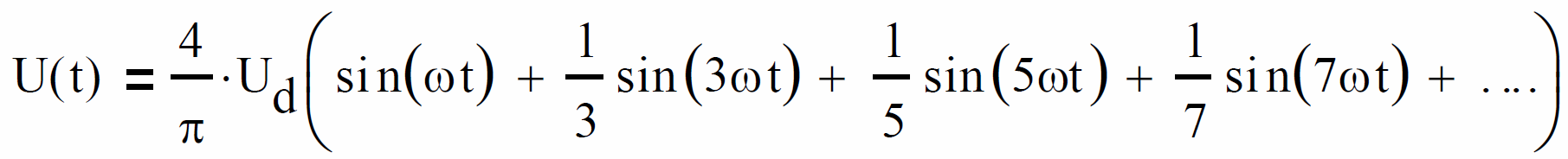
Nie przestrasz się tego wzoru. W dalsze subtelności nie będziemy wchodzić, między innymi dlatego, że w praktyce nie budujemy przebiegów przez dodawanie odpowiednio dobranych harmonicznych. W elektronice bardzo często przeprowadzamy natomiast operację odwrotną: rozkładamy przebiegi na elementarne składniki (za pomocą rozmaitych filtrów), a przynajmniej jesteśmy żywo zainteresowani tym, jakie składniki, inaczej: jakie harmoniczne zawarte są w rozmaitych przebiegach. Interesuje nas to również w przypadku aparatury audio, gdzie chodzi o to, żeby sprzęt jak najmniej zniekształcał, czyli żeby czysta sinusoida podana na wejście, na wyjściu też pojawiła się jako czysta sinusoida, bez żadnych dodatkowych harmonicznych. Natomiast w radiowej technice w.cz. sprawa bywa inna: czasem harmoniczne traktujemy jako składniki niepożądane, które trzeba usunąć, a czasem przeciwnie – wykorzystujemy właśnie jedną lub kilka harmonicznych.

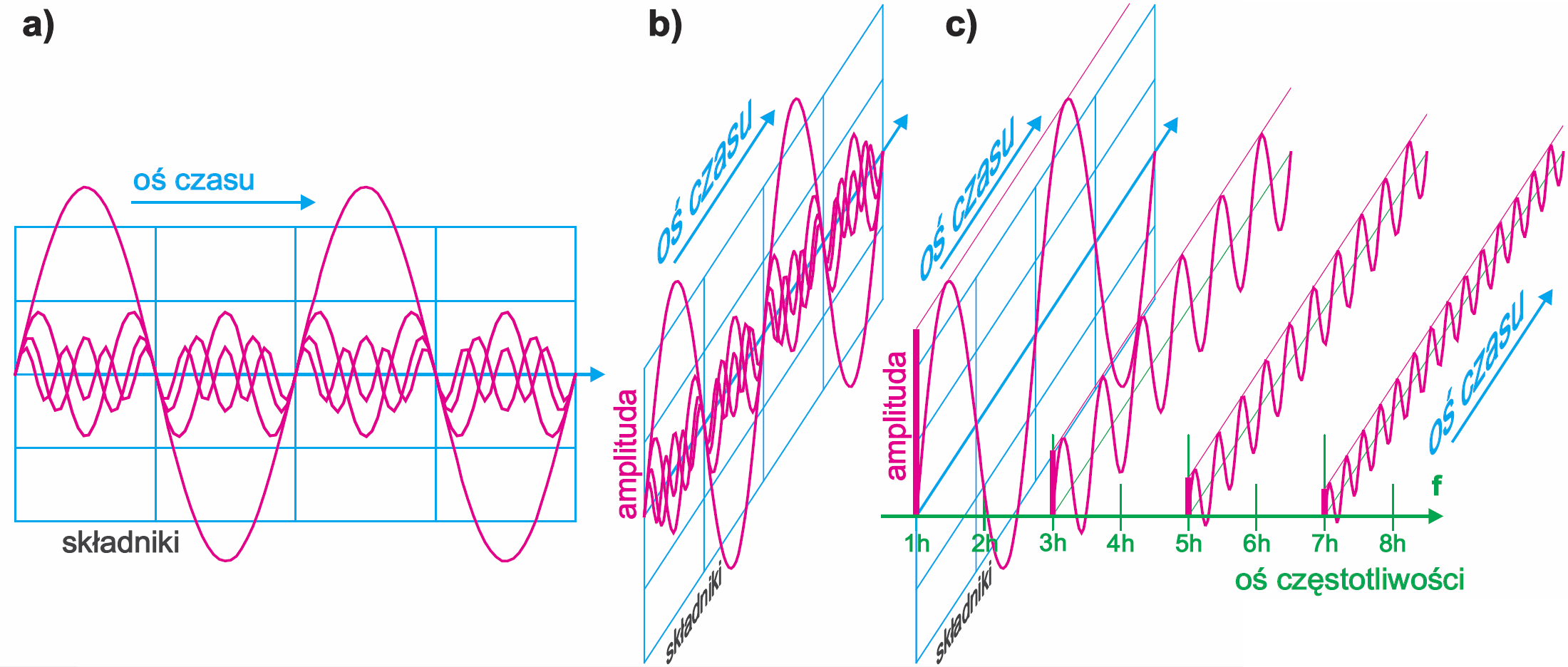
W szczegóły nie będziemy wchodzić, ale muszę zasygnalizować bardzo ważną sprawę. Otóż jeśli jakiś przebieg naprawdę składa się z sinusoidalnych składników elementarnych o częstotliwości podstawowej i o częstotliwościach harmonicznych, to zapewne można te elementarne składniki zbadać i zaprezentować. Tak jest, tylko w praktyce nie robi się tego tak, jak na rysunku 6, gdzie pozioma oś (oś X) jest osią czasu. Biorąc rzecz w uproszczeniu, poszczególne składniki są sinusoidami i nie ma potrzeby przedstawiać ich kształtu – wystarczy pokazać ich wielkość – np. amplitudę. Wyobraź sobie, że „stojący” rysunek 6 „obracamy” w lewo o 90 stopni i dorysowujemy nową oś poziomą, która będzie osią częstotliwości. „Rozsuwamy” poszczególne składniki zgodnie z ich częstotliwością. Opisywane właśnie kroki ilustruje rysunek 7.

Na koniec nie rysujemy już sinusoid, tylko zaznaczamy słupkami wielkość poszczególnych składników. Otrzymujemy charakterystykę spektralną, inaczej mówiąc widmo przebiegu – lub zawartość widmową. Czasem na górze słupków dodajemy małe „poprzeczki”, jak na rysunku 8.

Taką analizę i „rozłożenie przebiegu na czynniki pierwsze” można wykonać w różny sposób: albo analogowo, albo na drodze cyfrowej. Dziś takie analizy przeprowadza się gównie na drodze cyfrowej.

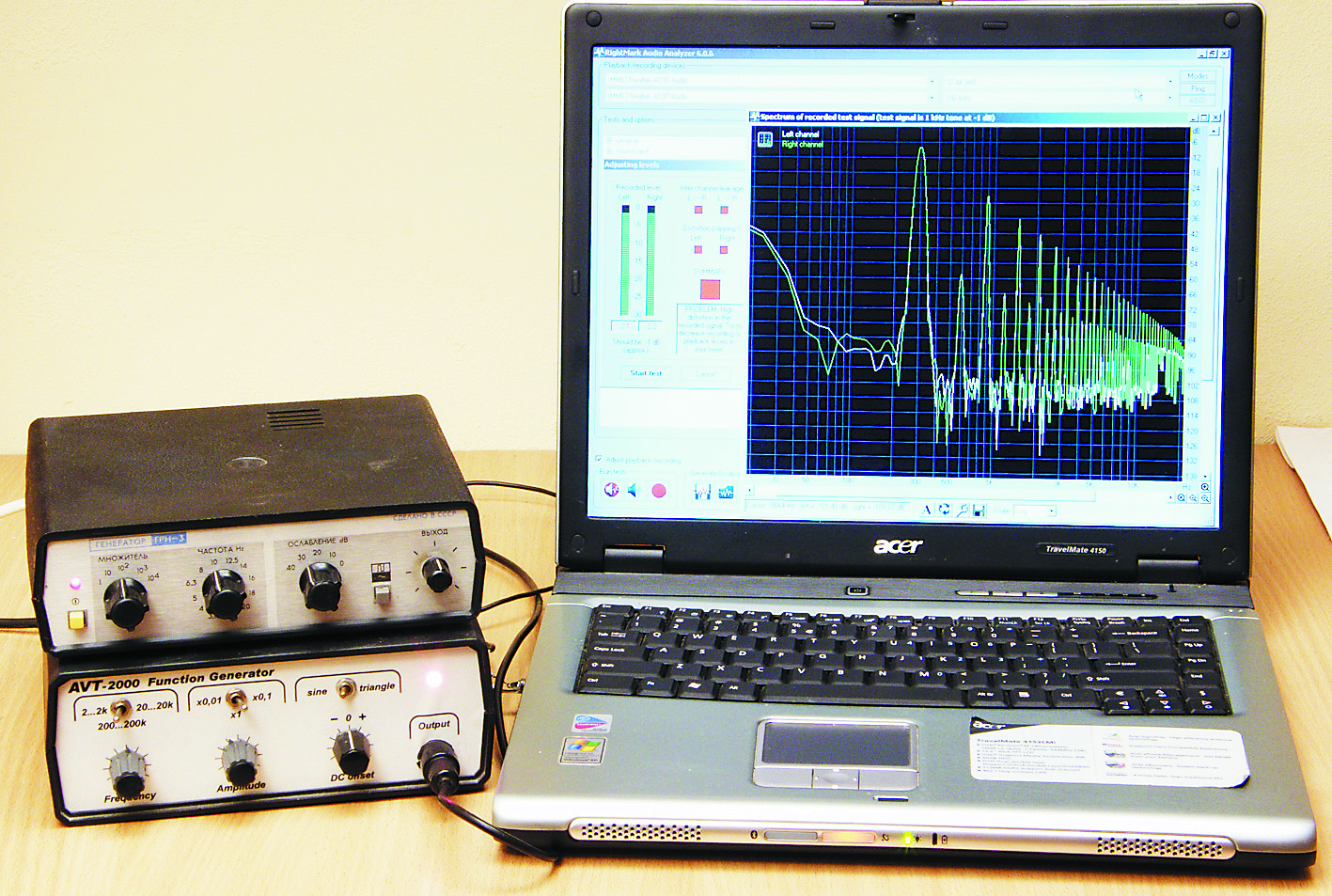
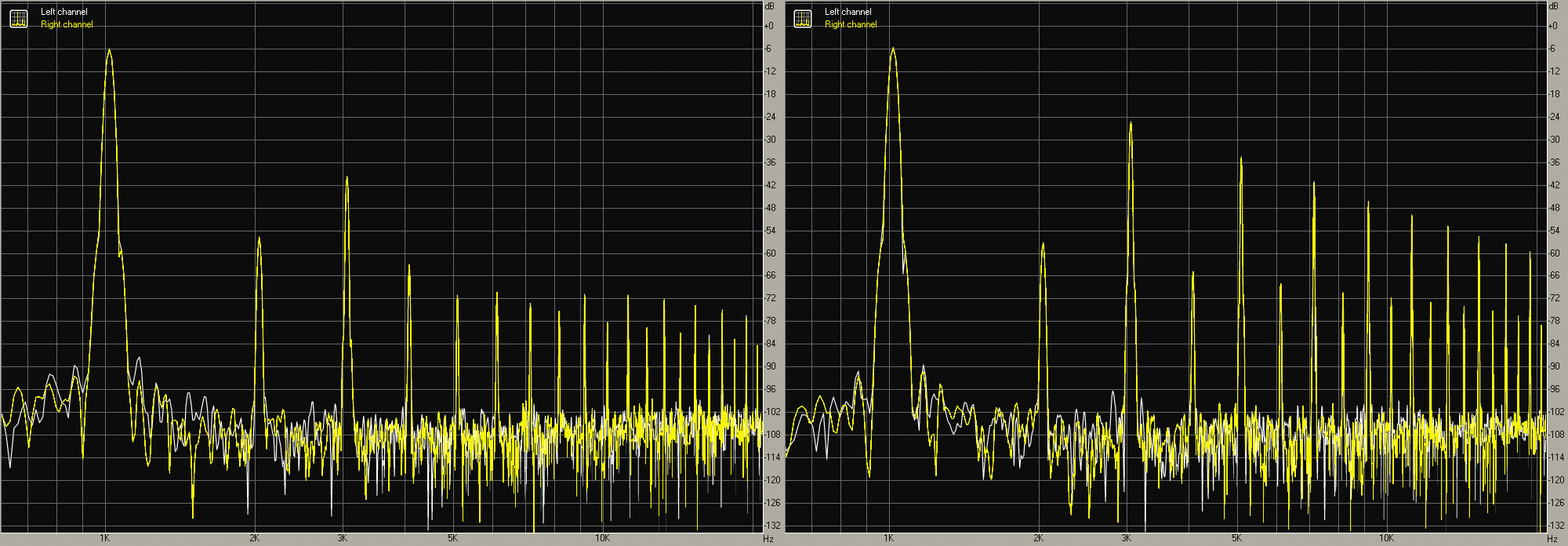
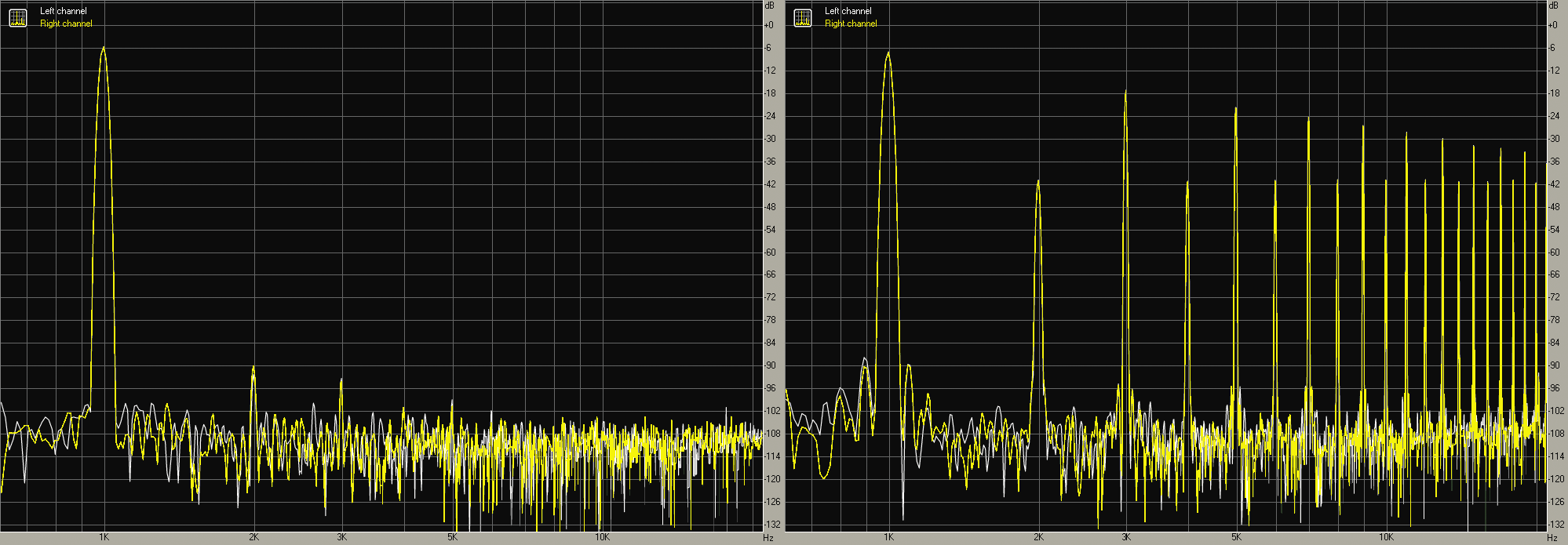
Być może słyszałeś już o FFT – Fast Fourier Transform, czyli algorytmach szybkiej transformaty Fouriera oraz o oknach Blackmana, Hamminga, Hanninga itp. W szczegóły nie wchodzimy, w każdym razie z wynikami takiego rozkładania na elementarne składniki mamy do czynienia dość często. Fotografia 9 pokazuje tego rodzaju pomiary dwóch najprawdziwszych analogowych generatorów.

Rysunek 10 prezentuje zrzut z ekranu komputera: obliczoną w popularnym programie RightMark Audio Analyzer zawartość widmową przebiegów sinusoidalnego i trójkątnego z generatora funkcji z kostką XR2206, natomiast rysunek 11 to podobny zrzut pokazujący skład widmowy przebiegów sinusoidalnego i prostokątnego ze starego generatora radzieckiego (litewskiego) z mostkiem Wiena i żarówką. Jak widać, sinusoida pochodząca z generatora z mostkiem Wiena jest bardzo „czysta” i zawiera niewiele dodatkowych składników – zniekształceń. Nie można tego powiedzieć o sinusoidzie pochodzącej z kostki generatora funkcyjnego XR2206, która okazuje się być w znacznym stopniu zniekształcona, czyli zawiera dodatkowe harmoniczne.

Nie przejmuj się, że tak daleko odeszliśmy od omawiania podstawowych właściwości kondensatorów. Ale to nie przypadek. Taka wiedza jest konieczna, żebyś był przekonany, iż sinusoida to najprostszy, elementarny przebieg, i żebyś dobrze rozumiał zachowanie i właściwości kondensatorów, które pracują właśnie przy przebiegach zmiennych. Ale to wcale nie koniec potrzebnej przy tym wiedzy teoretycznej.

W następnym odcinku jeszcze nie wrócimy do właściwości kondensatorów. Zajmiemy się kolejnymi ważnymi informacjami o sposobach określania cech przebiegów zmiennych. Dopiero potem będziemy mogli z pełną świadomością omówić bardzo ważne właściwości kondensatorów i obwodów, zawierających kondensatory.

Piotr Górecki