Elektronika (nie tylko) dla informatyków (7) Faza, wektory, wartość skuteczna

W poprzednim wykładzie zamiast analizować podstawowe właściwości kondensatorów, zajęliśmy się prostymi i „nieprostymi” przebiegami zmiennymi. Okazało się, że sinusoida jest podstawowym, najprostszym przebiegiem i że każdy inny przebieg zmienny jest w istocie złożeniem pewnej liczby przebiegów sinusoidalnych.

Zrobiliśmy wycieczkę w dziedzinę matematyki i algorytmów cyfrowego przetwarzania danych. W tym wykładzie wracamy do elektroniki, ale jeszcze nie do właściwości kondensatorów.

Faza i wektory

Większość początkujących ma kłopot ze zrozumieniem wykresów wskazowych, dość często spotykanych w elektronice. Tymczasem przy omawianiu kondensatorów są one wręcz niezbędne do zrozumienia i przeprowadzania obliczeń. Faktem jest, że na początku takie określenia jak: przesuniecie fazowe, prąd wyprzedza napięcie albo prąd opóźnia się względem napięcia, mogą wręcz budzić grozę i kojarzyć się z magią, a nie elektroniką. Bo niby jak prąd może wyprzedzić napięcie? A jeśli wyprzedza, to jak jest z zasadą przyczynowości? Czy „skutek może pojawić się wcześniej niż przyczyna”?

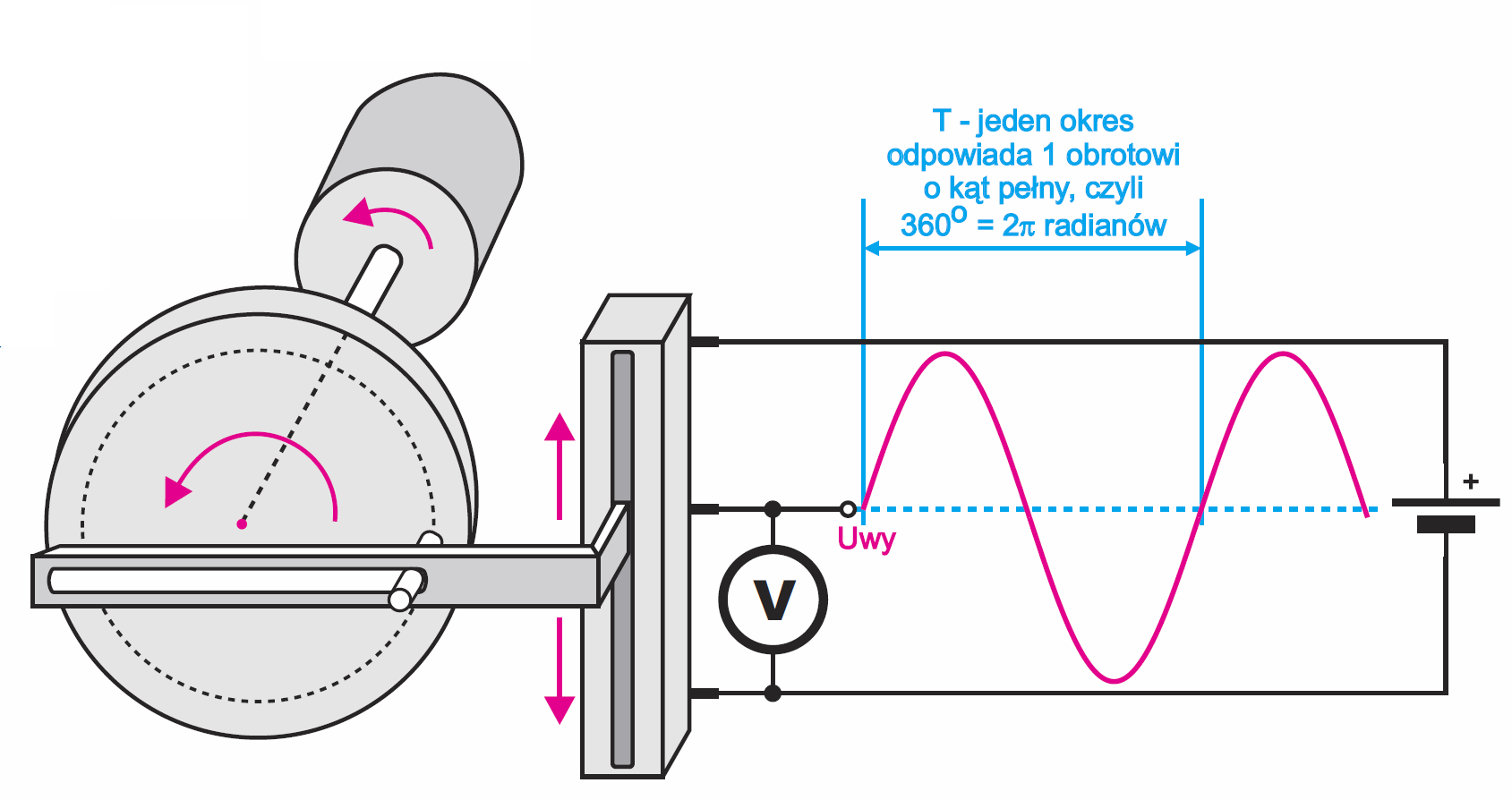
Tego rodzaju pytania nurtują niejednego początkującego. Tymczasem wystarczy dobrze zacząć, ponieważ zagadnienie wcale nie jest trudne i nie ma mowy o złamaniu prawa przyczynowości. Wystarczy przyjrzeć się właściwościom przebiegów zmiennych, w szczególności sinusoidalnego. Najpierw powróćmy do związku ruchu obrotowego z przebiegiem sinusoidalnym. Otóż trzeba przypomnieć, że zgodnie z rysunkiem 1, jeden okres przebiegu odpowiada jednemu obrotowi, czyli kątowi pełnemu: 360 stopni, inaczej 2π radianów. A tak przy okazji: nie dziw się więc, że we wzorach pojawia się 2π. Mówiąc obrazowo, we wzorach te 2π reprezentuje jeden obrót. Nie musisz wnikać w dalsze szczegóły.

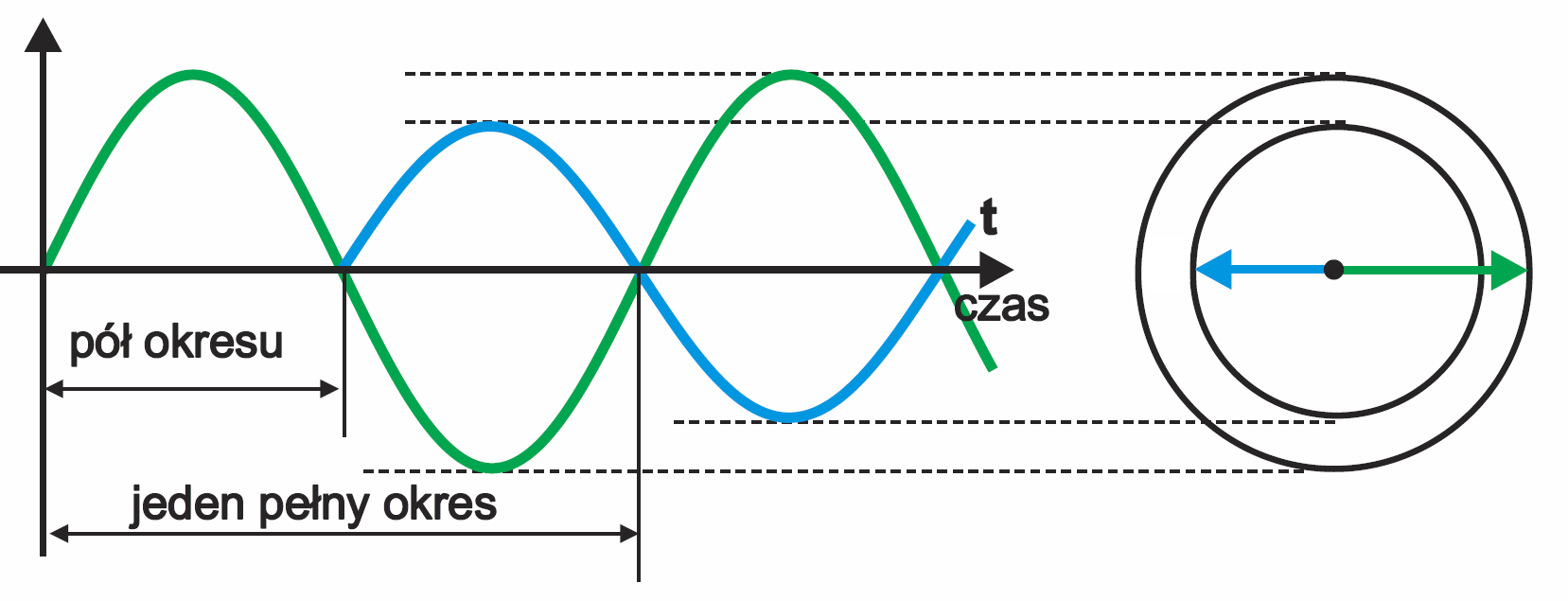
Co ważniejsze, jeśli jeden obrót o kąt pełny daje jeden okres przebiegu, nie dziw się też, że w elektronice zamiast mówić o części okresu, mówimy o kątach, a czasem także o prędkości kątowej w radianach na sekundę. Dotyczy to w szczególności kątów przesunięcia między przebiegami. I tak na przykład (przesunięcie o) pół okresu to (przesunięcie o) 180 stopni, czyli π radianów. Możemy to narysować w sposób klasyczny, lewa część rysunku 2, gdzie niebieski przebieg wyraźnie zaczyna się w połowie okresu przebiegu zielonego. Ale możemy radykalnie uprościć rysunki i zaznaczyć tylko strzałki, gdzie długość strzałki reprezentuje wielkość przebiegu, a kąt między nimi pokazuje przesunięcie – prawa część rysunku 2. Jeśli nie rozumiesz takiej idei, przeczytaj dokładnie dalsze wyjaśnienia.

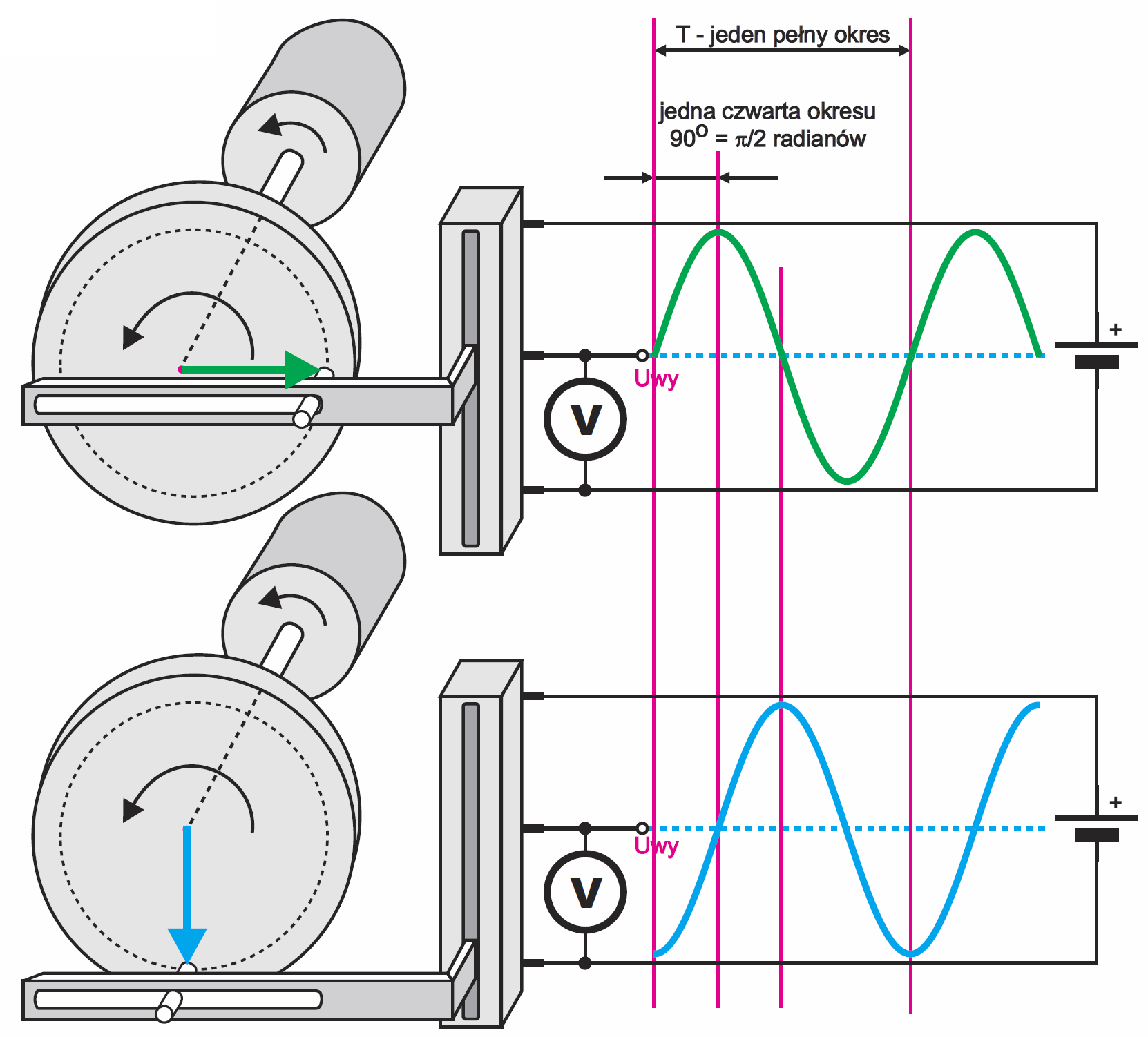
Tak naprawdę to obie strzałki na wykresach wskazowych powinny się obracać z prędkością odpowiadającą częstotliwości, niczym wskazówki zegara, tylko w kierunku przeciwnym do ruchu wskazówek zegara. Możemy sobie wyobrazić, że na dwóch wirujących tarczach narysowane są strzałki o długości proporcjonalnej do wielkości przebiegu i my fotografujemy to z użyciem lampy błyskowej, czym „zamrażamy” chwilowy stan – patrz rysunek 3. Potem nakładamy na siebie dwa zdjęcia tarcz i rysujemy na papierze „zamrożony”, chwilowy stan obu tarcz – w sumie tylko dwie strzałki.

Oczywiście częstotliwość obu przebiegów jest taka sama, a interesuje nas amplituda i właśnie wzajemne przesunięcie (opóźnienie) obu przebiegów. Co ważne, „fotografujemy” sprytnie, a nie byle jak: otóż jeden z przebiegów jest niejako przebiegiem odniesienia, a interesują nas właściwości drugiego przebiegu względem pierwszego. Na przykład na wejście wzmacniacza podajemy przebieg sinusoidalny i ciekawi nas, jak ma się przebieg wyjściowy do wejściowego. Wtedy przebieg wejściowy jest przebiegiem odniesienia i na „fotografii” reprezentujący go wektor będzie skierowany poziomo, w prawo (zielony na rysunkach 1, 2).

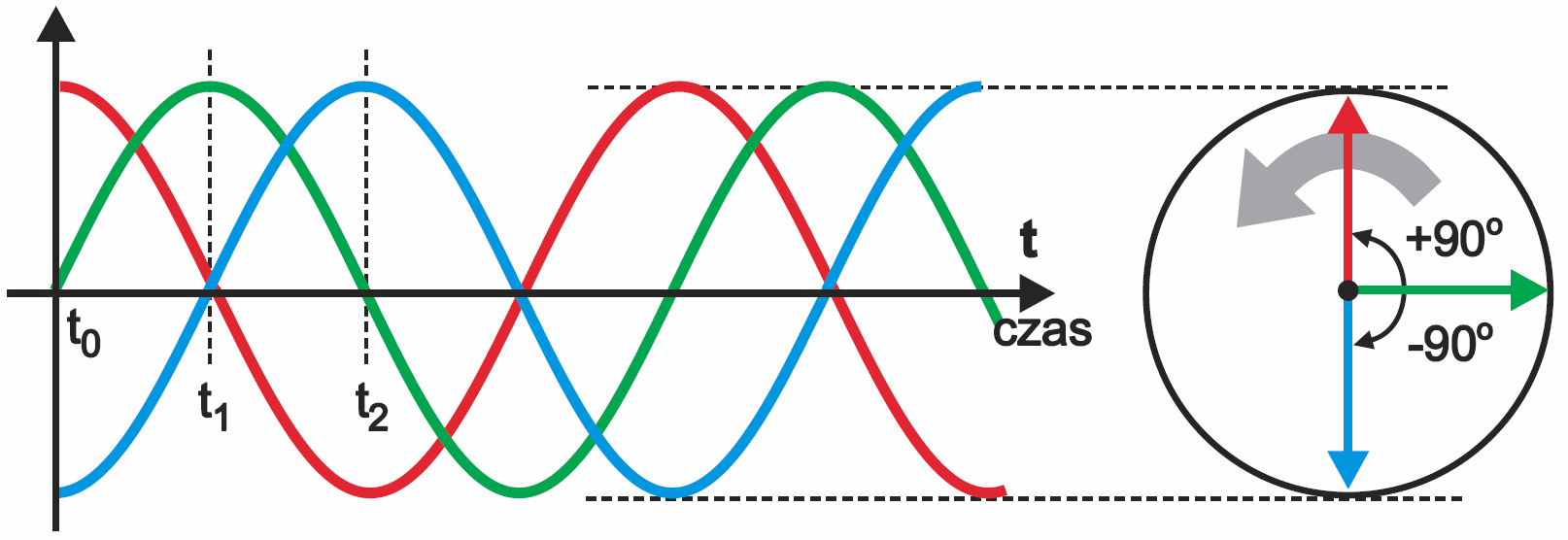
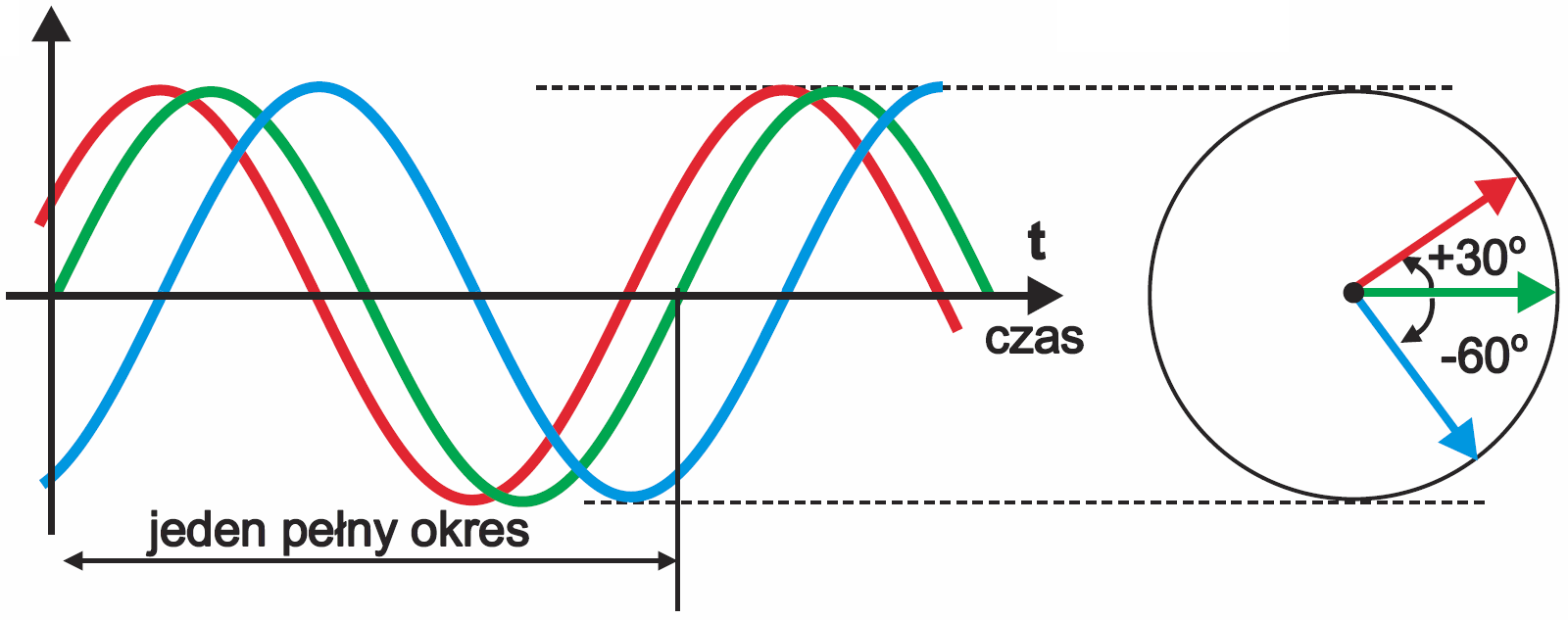
Popatrz na rysunek 4. Zielony przebieg znów jest przebiegiem odniesienia. Zwróć uwagę, że czerwony przebieg osiąga maksimum w chwili t₀, zielony w nieco późniejszej chwili t₁, a niebieski w jeszcze późniejszej chwili t₂. W związku z tym możemy powiedzieć, że czerwony przebieg wyprzedza zielony przebieg odniesienia. Natomiast przebieg niebieski jest opóźniony względem zielonego przebiegu odniesienia. Przesunięcie o ćwierć okresu to przesunięcie o kąt 90 stopni, czyli π/2 radianów – patrz rysunek 3.

No tak, ale przesunięcie może być dodatnie lub ujemne. I w związku z tym kąt zaznaczony na wykresie wskazowym będzie dodatni lub ujemny. Jeśli masz wątpliwości, wróć jeszcze raz do rysunku 3 i zastanów się, jak na rysunku 3 należałoby narysować czerwony przebieg?

Tak – czerwona strzałka na tarczy byłaby skierowana w górę, jak na rysunku 4.

Przypominam, że kierunek przeciwny do ruchu wskazówek zegara nazywamy kierunkiem dodatnim. Możemy też zaznaczyć kąty ujemne (zgodnie z ruchem wskazówek zegara). Tak bowiem przyjęło się w matematyce rysować i oznaczać kąty. Dwa dalsze przykłady pokazane są na rysunku 5.

Ale może masz zakodowane głębokie przekonanie, że opóźnienie między przebiegami należy podawać w jednostkach czasu, ponieważ „naturalną” miarą opóźnienia jest czas, a nie kąt. Nie dziwię się – to może być silne, mocno utrwalone przekonanie. Mam jednak nadzieje, że podane właśnie rysunki przekonają Cię, że podawanie opóźnienia czy wyprzedzenia w postaci kąta też jest jak najbardziej sensowne i w sumie naturalne. W pewnych sytuacjach rzeczywiście lepiej podawać opóźnienie w jednostkach czasu, np. w mikrosekundach czy milisekundach. Ale w wielu innych przypadkach jaśniejszy obraz sytuacji daje podawanie opóźnienia właśnie w postaci kąta. A tak naprawdę chodzi o to samo: można łatwo przeliczyć czas na kąt i na odwrót. Trzeba tylko pamiętać, że chodzi o przebieg o jakiejś konkretnej częstotliwości f, którego okres wynosi T. I właśnie czas T odpowiada kątowi pełnemu. Jeśli kąt wyrazimy w stopniach, mamy:

T = 360°
jeśli w radianach:
T = 2π

Dla sąsiednich przebiegów z rysunku 4 różnica faz wynosi 90 stopni, czyli π/2. Jeśli na przykład częstotliwość przebiegów wynosi 1 kHz, to okres jest równy 1 ms. Jeśli 1 ms = 2π, to π/2 = 0,25 ms. Opóźnienie o kąt 90 stopni wynosi więc w tym konkretnym przypadku 0,25 ms. Natomiast opóźnienie o kąt 120 stopni, czyli o 1/3 okresu, wyniesie w tym przypadku 0,333(3) ms.

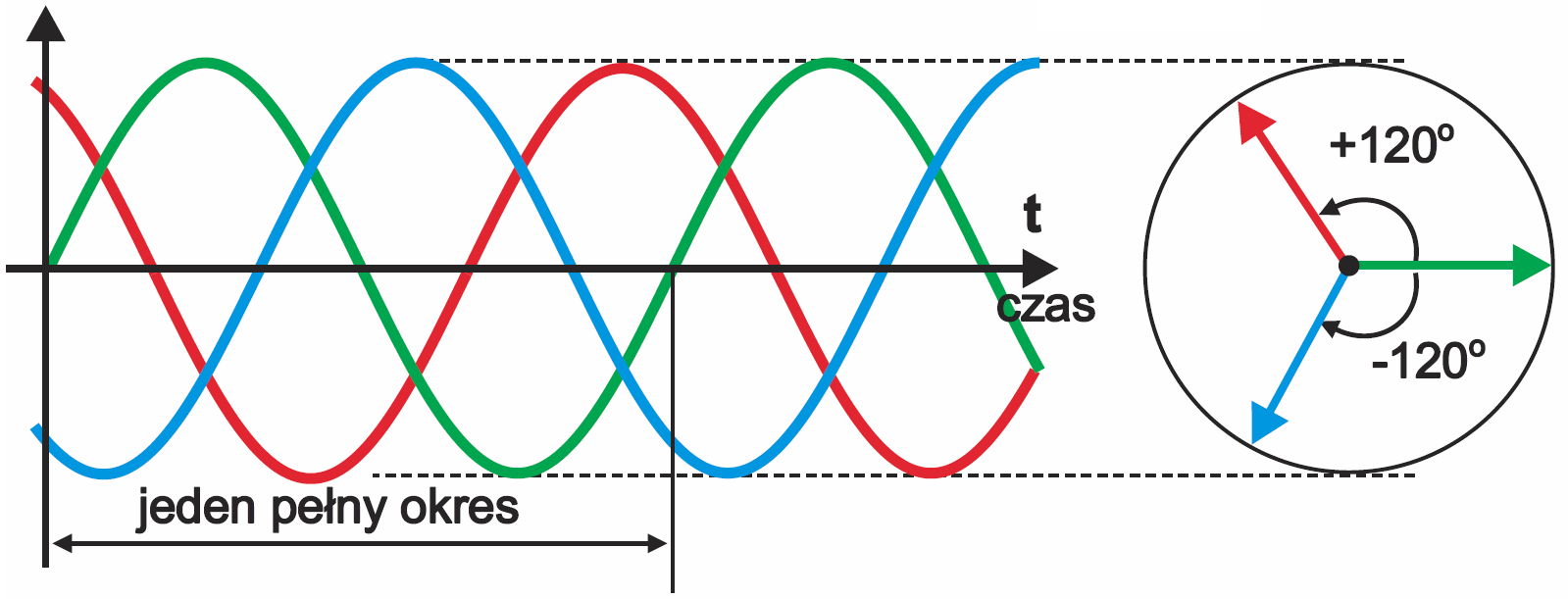
Oczywiście przy innej częstotliwości opóźnienie o taki sam kąt, wyrażone w jednostkach czasu, będzie inne. Na przykład dwie fazy przebiegu trójfazowego w sieci energetycznej przesunięte są o jedną trzecią okresu, czyli o 120 stopni (2π/3). Na wykresie wskazowym zaznaczymy to jak na rysunku 6. Częstotliwość to oczywiście 50 Hz, więc okres wynosi 20 ms. Opóźnienie między sąsiednimi fazami jest równe 20ms/3 = 6,66(6) ms.

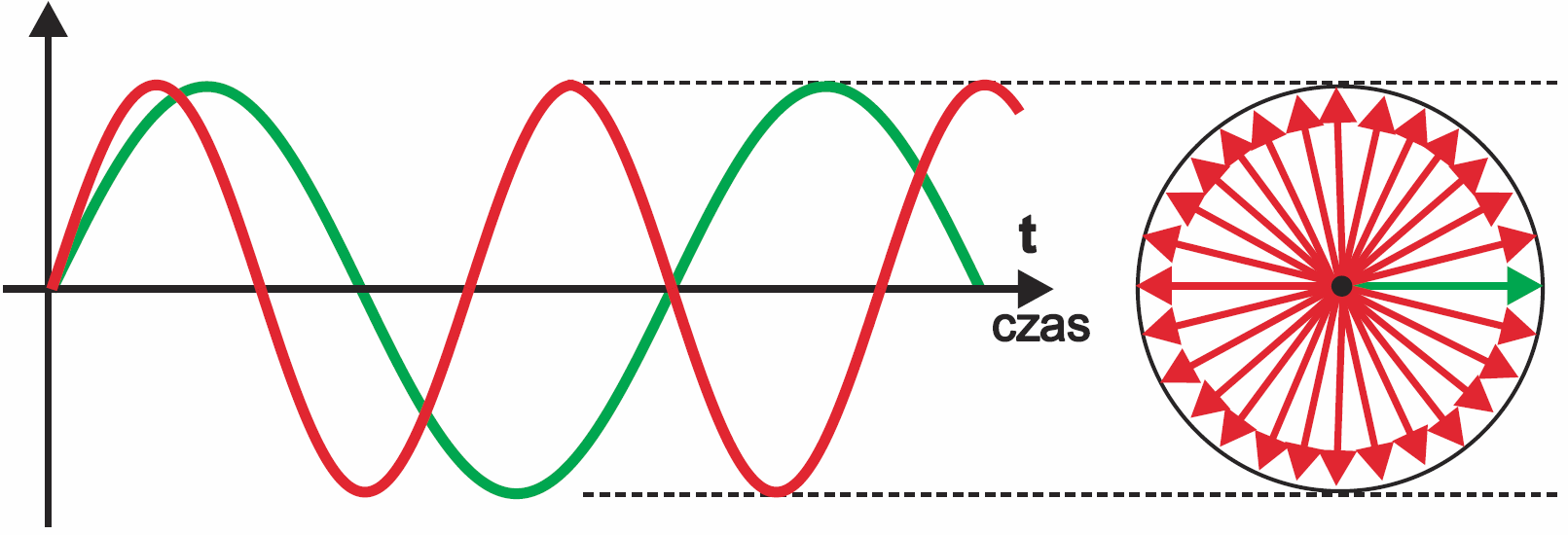
Wszyscy Czytelnicy powinni rozumieć, że takie rozważania i wykresy wskazowe mają sens tylko dla przebiegów sinusoidalnych o identycznej częstotliwości. Oczywiście nie można mówić o jednej konkretnej wartości przesunięcia czy opóźnienia, jeśli częstotliwości (prędkości wirowania) byłyby różne. Nie można narysować wykresu wskazowego dla dwóch przebiegów o różnej częstotliwości, czyli dla różnych prędkości wirowania. Gdybyśmy chcieli sfotografować wskazówki na tarczach wirujących z odmiennymi prędkościami (rysunek 3), to kąty między nimi co chwila byłyby inne – rysunek 7.

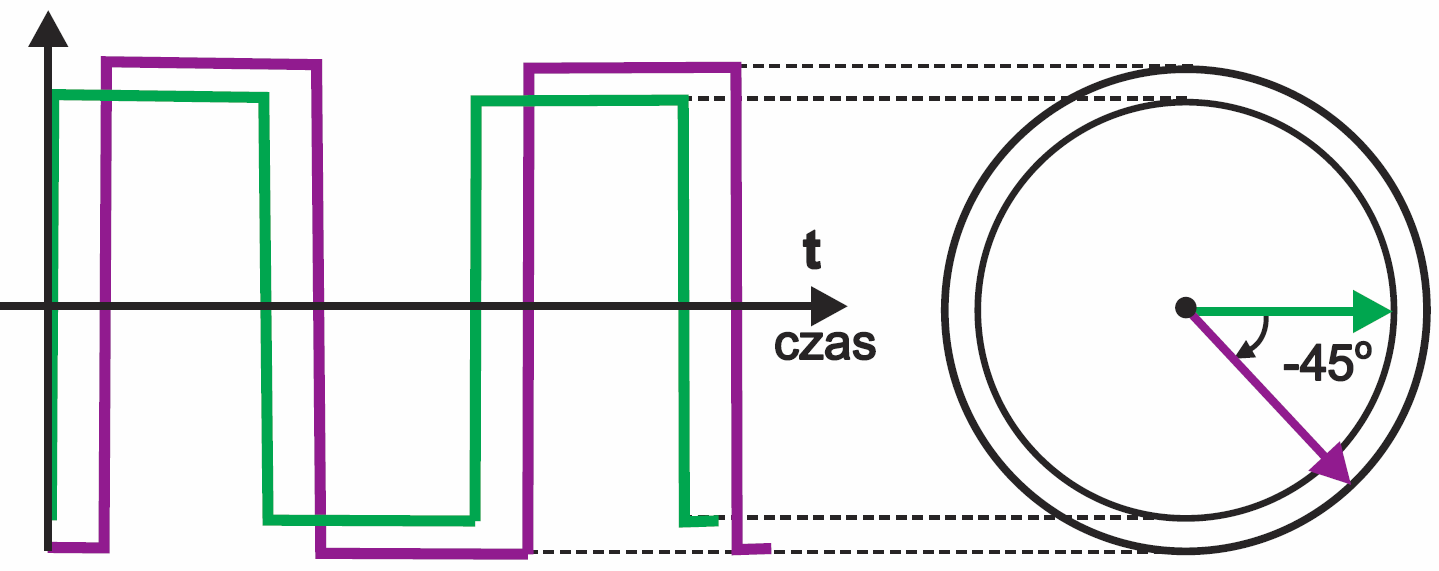
Warto też podkreślić, iż omawianymi właśnie wykresami posługujemy się przede wszystkim w odniesieniu do przebiegów sinusoidalnych, co dobrze odzwierciedla rzeczywistość, bo przebieg sinusoidalny jest silnie związany z ruchem obrotowym. Czasem spotyka się też podawanie opóźnienia czy przesunięcia w postaci kąta (jako części okresu) także w przypadku przebiegów o innych kształtach, na przykład przebiegów prostokątnych – rysunek 8.

Wprawdzie jakaś logika w tym jest, jednak takie podejście nie jest do końca ścisłe, a niekiedy może nawet wprowadzać w błąd. Dlatego wykresy wskazowe i miarę kątową należy raczej stosować jedynie do opisu przebiegów sinusoidalnych i innych wielkości mających z nimi bezpośredni związek.

Wartość skuteczna

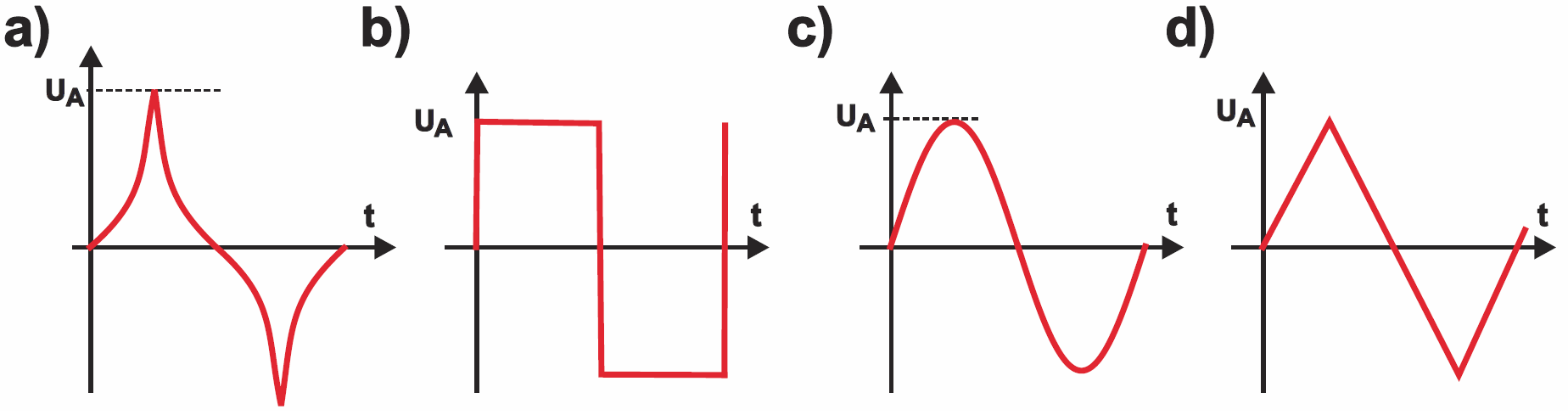
Omawiając kondensatory, musimy niechybnie od prądu stałego przejść do przebiegów zmiennych i do kolejnej bardzo ważnej sprawy. Otóż przebiegi zmienne mogą mieć najróżniejsze kształty – rysunek 9 pokazuje kilka przykładów. W przypadku napięcia i prądu stałego nie było żadnych wątpliwości, co do ich wartości. A jak myślisz, które z tych napięć zmiennych ma największą wartość? Czy wysoki, ale bardzo „chudy” przebieg z rysunku 9a, czy może „przysadzisty i krępy” przebieg środkowy? A może przebieg sinusoidalny z rysunku 9c?

Odpowiedź nie jest łatwa. Bo co to znaczy „ma największą wartość”?

Największą amplitudę ma niewątpliwie przebieg z rysunku 9a. Ale jest bardzo „chudy” i to budzi wątpliwości, czy rzeczywiście ma on dużą „siłę oddziaływania”. Chyba już widzisz jasno, że amplituda nie jest jedyną i ostateczną miarą przebiegów zmiennych.

Co jest więc „obiektywną miarą wielkości” przebiegów zmiennych, w tym ich napięcia i natężenia?

Nie wchodząc w szczegóły, powiem tylko, że podstawą oceny jest moc i ilość ciepła. W sumie chodzi o skutek – skutek cieplny, jaki dany przebieg wywołuje albo może wywołać. I dlatego, że chodzi o skutek cieplny, mówimy o wartości skutecznej napięcia czy prądu. Według starszej, łatwo przyswajalnej definicji, wartość skuteczna danego napięcia (prądu) zmiennego to taka wartość napięcia (prądu) stałego, który w rezystancji obciążenia wywoła wydzielenie tej samej ilości ciepła, co badany przebieg zmienny.

Temat wartości skutecznej jest w sumie dość obszerny i ma związek ze skrótem RMS, oznaczającym właśnie wartość skuteczną. Nie będziemy się jednak w to wgłębiać. Zapamiętaj tylko elementarne wiadomości:

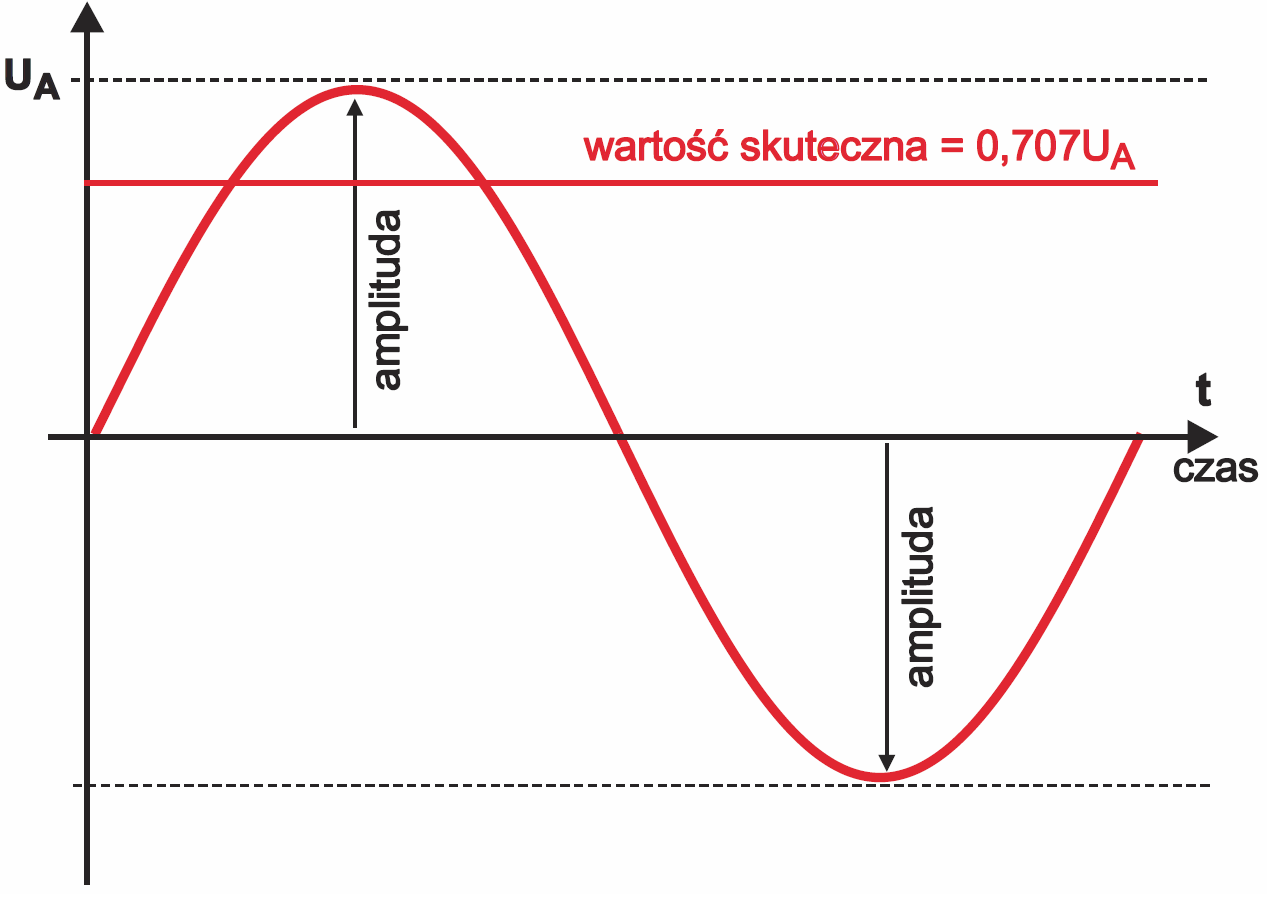
Tylko dla przebiegu prostokątnego (rysunek 9b) wartość skuteczna jest równa amplitudzie, dla wszystkich innych wartość skuteczna jest mniejsza od amplitudy. Na przykład dla przebiegu trójkątnego z rysunku 9d wartość skuteczna jest pierwiastek z 3 razy mniejsza od amplitudy. To w praktyce nie będzie Ci potrzebne – zapamiętaj natomiast raz na zawsze, że wartość skuteczna przebiegu sinusoidalnego jest pierwiastek z dwóch razy mniejsza od amplitudy. Stosowne zależności pokazuje rysunek 10.

Pierwiastek z dwóch to liczba niewymierna i ułamek nieskończony 1,4142135623730 950488016887242097… W praktyce zależność między amplitudą i wartością skuteczną podajemy w przybliżeniu:
U_sk = U_a/1,41 = 0,707 U_a
I_sk = I_a/1,41 = 0,707 I_a
ewentualnie z mniejszą dokładnością:
U_sk = U_a/1,4 = 0,7 U_a
I_sk = I_a/1,4 = 0,7 I_a

Przy okazji warto dodać, że wartość skuteczna nie jest równa wartości średniej. Wartość średnia przebiegu sinusoidalnego wynosi… zero, a wartość średnia połówki okresu (a także modułu, czyli „wyprostowanej” sinusoidy) 2/π, czyli 0,6366…

Zapamiętaj też, że jeśli gdzieś podana jest wartość napięcia lub prądu zmiennego, to w ogromnej większości przypadków jest to właśnie wartość skuteczna, a nie amplituda. Dlatego wartości skutecznej przebiegów zmiennych zazwyczaj nie oznaczamy ani U_sk, I_sk, ani też U_RMS, I_RMS, tylko piszemy po prostu U, I.

Na przykład wiadomo, że napięcie w sieci energetycznej wynosi obecnie 230 V. Jest to wartość skuteczna, a więc amplituda nieodkształconej, czystej sinusoidy wynosi 325 V, a wartość międzyszczytowa 650 V. Do tego należy dodać, że w wielu zastosowaniach drugim istotnym parametrem przebiegu zmiennego, obok wartości skutecznej, jest jego częstotliwość.

Mając takie informacje, możemy powrócić do kondensatora i problemu jego oporności. Zajmiemy się tym w następnym odcinku.

Piotr Górecki