Elektronika (nie tylko) dla informatyków (8) Oporność kondensatora

Ostatni wykład jak i poprzednie zawierały dużą dawkę wiedzy teoretycznej. Jest ona niezbędna, jeśli chcesz dobrze zrozumieć właściwości kondensatorów oraz licznych układów, w których są stosowane. Wracamy do parametru na pozór oczywistego, jakim jest oporność kondensatora.

Dla wielu Czytelników przedstawione informacje nie są nowością, jednak dla innych, nie tylko młodych fascynatów informatyki, będzie to wejście w nieznany świat. Dobre zrozumienie impedancji, sposobów graficznej reprezentacji oraz związanych z tym obliczeń, jest absolutnie niezbędnym fundamentem elektroniki.

Oporność kondensatora raz jeszcze

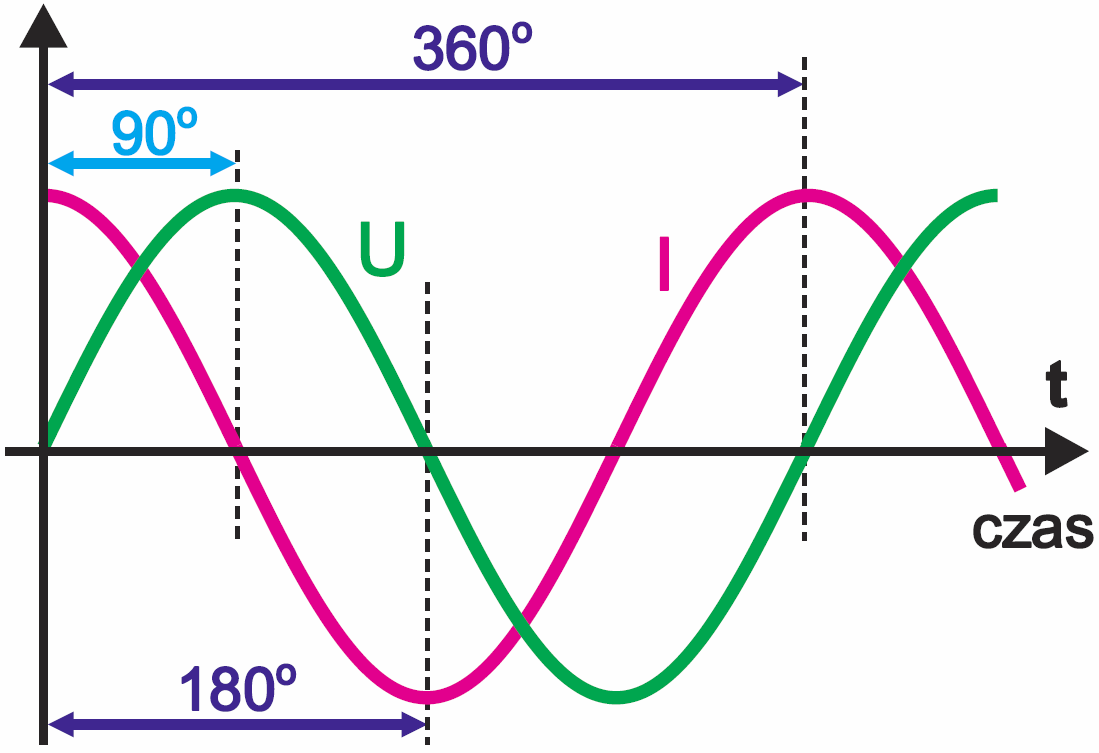
Analiza elementarnych właściwości kondensatora doprowadziła nas w jednym z wcześniejszych odcinków do wniosku, że tylko w jednym przypadku, przy przebiegu sinusoidalnym, kształt prądu płynącego przez kondensator jest taki sam jak przebieg napięcia na kondensatorze. Pokazują to wcześniejsze rysunki 4, 5, 6 w tym wykładzie. A jeśli mamy sinusoidalne przebiegi prądu i napięcia, to możemy łatwo policzyć ich wartości skuteczne, a stąd już jeden maleńki krok do oporności jako stosunku U/I.

Można bowiem powiedzieć, że oporność to stosunek napięcia i prądu (U/I), a konkretnie stosunek wartości skutecznych napięcia i prądu. Jednak ze względu na przesunięcie fazy, oporności kondensatora na pewno nie powinniśmy nazywać rezystancją (porównaj wcześniejsze rysunki 7 i 8 w tym wykładzie). Zapewne wiesz, że nazywamy ją reaktancją pojemnościową i oznaczamy X_C.

Wcześniej na podstawie rysunku 7 w tym wykładzie ustaliliśmy, że oporność kondensatora jest odwrotnie proporcjonalna do pojemności. Czym większa pojemność, tym mniejsza oporność – to jest proste i oczywiste.

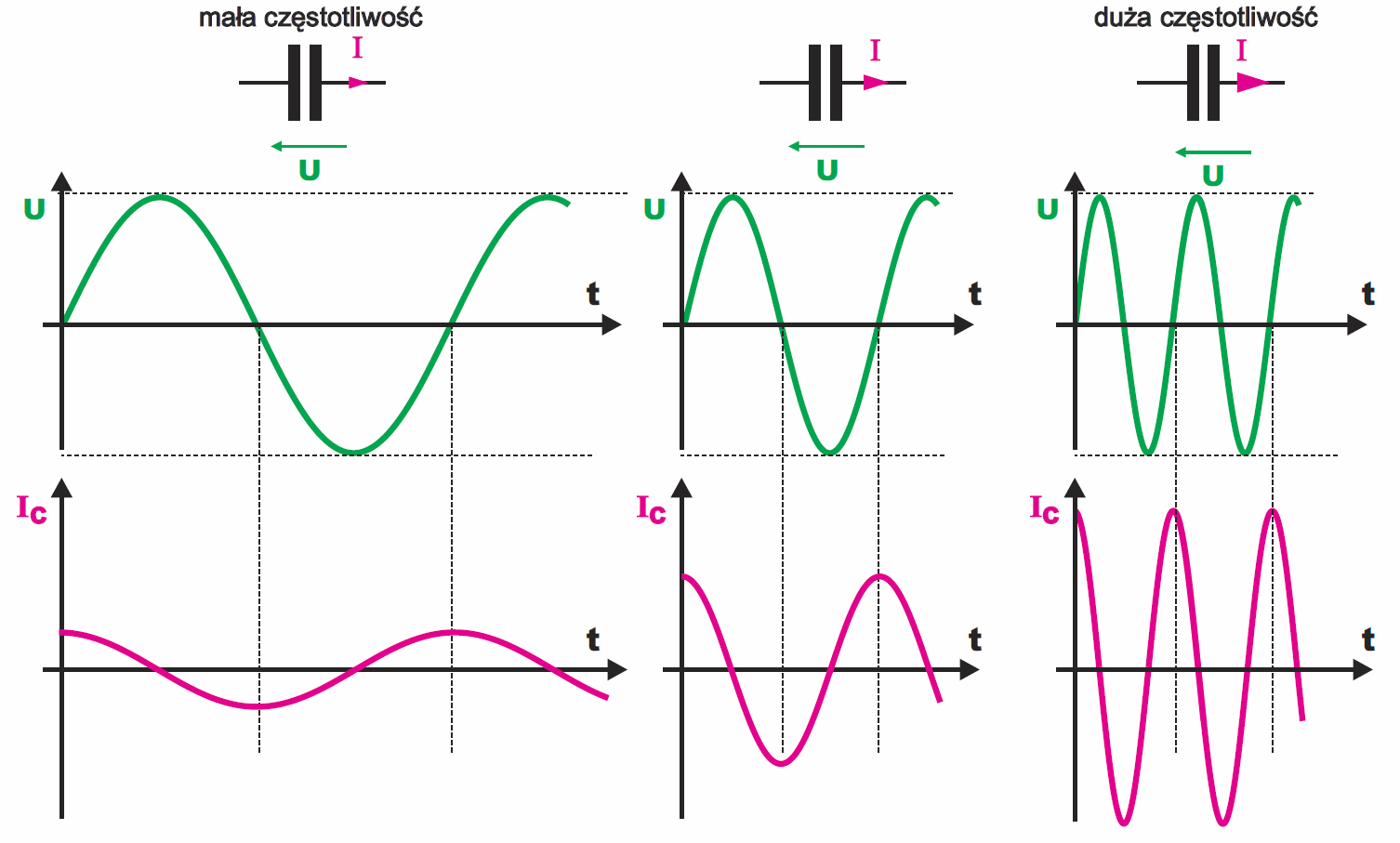
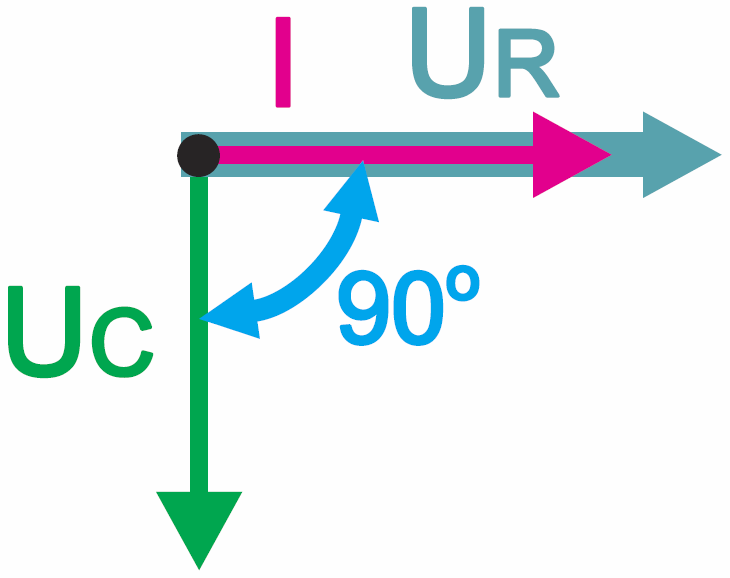
A teraz kolejny raz przypominam podstawową zależność: prąd płynący przez kondensator jest proporcjonalny do szybkości zmian napięcia. Prosty przykład masz na rysunku 1.

Czym większa częstotliwość, tym większa szybkość zmian napięcia i tym większy prąd. I to też jest oczywiste, ale co to mówi o oporności kondensatora, będącej stosunkiem U/I?

Otóż rysunek 1 wskazuje, że oporność kondensatora nie jest stała – zmniejsza się ze wzrostem częstotliwości. Oporność kondensatora dla przebiegów sinusoidalnych jest odwrotnie proporcjonalna do szybkości zmian napięcia (i częstotliwości).

A jeśli tak, to nie będzie Cię już dziwić wzór:

X_c = 1/ω

Litera ω oznacza tak zwaną pulsację. I właśnie pulsacja reprezentuje szybkość zmian. W praktyce zamiast pulsacji do obliczeń wykorzystujemy częstotliwość f. Ponieważ ω = 2π, otrzymujemy znany wzór na reaktancję kondensatora:

X_c = 1/2πfC

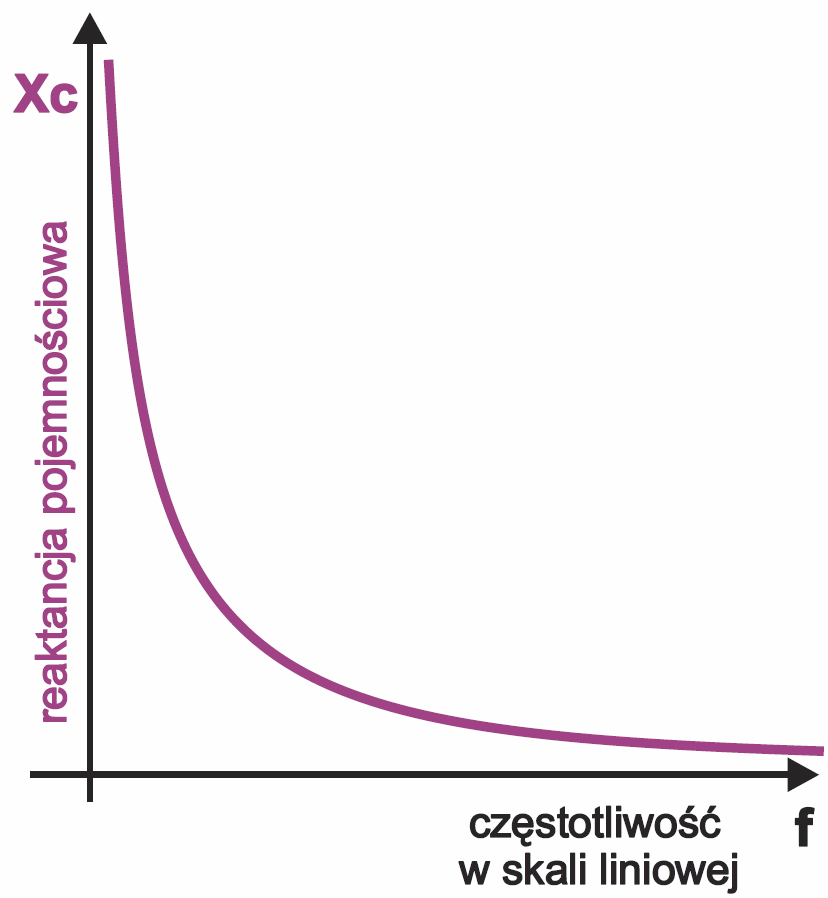
Rysunek 2 pokazuje zależność reaktancji X_c od częstotliwości, narysowany w skali liniowej.

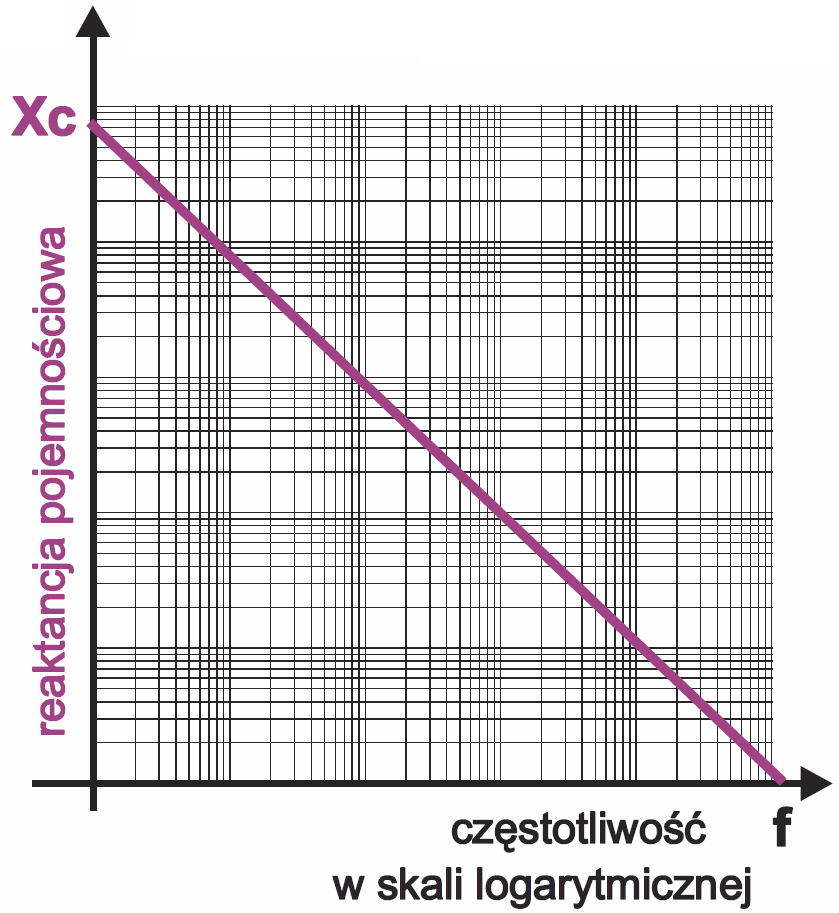
Nie wygląda to interesująco. Jeśli jednak tę samą zależność narysujemy w skali logarytmicznej, okaże się, że wykresem jest linia prosta – rysunek 3. Dość często spotyka się podobne „prostoliniowe” wykresy, wynikające z właściwości reaktancji pojemnościowej.

Znając oporność X_c, możemy korzystać z prawa Ohma:
I = U/X_c        U = I×X_c        X_c = U/I
gdzie U, I to oczywiście wartości skuteczne przebiegu sinusoidalnego.

Jeśli teraz uważasz, że już doskonale rozumiesz i czujesz intuicyjnie właściwości kondensatorów, muszę Ci zepsuć dobry nastrój.

Nieprzypadkowo tyle uwagi poświęciliśmy sprawie rozkładania złożonych przebiegów na elementarne sinusoidalne składowe harmoniczne. Nieprzypadkowo też zajmowaliśmy się wykresami wskazowymi. Od razu zasygnalizuję dwa poważne problemy.

Otóż kondensatory rzadko pracują przy czystych przebiegach sinusoidalnych, a jak wiesz, przebiegi o innych kształtach są w istocie złożeniem wielu „elementarnych” przebiegów sinusoidalnych o odpowiednich częstotliwościach. Tymczasem wzór X_c = 1/2πfC dotyczy tylko oporności dla czystego przebiegu sinusoidalnego o częstotliwości f. A jeśli roboczy przebieg tak naprawdę składa się z szeregu sinusoid o różnych częstotliwościach, to należałoby obliczać oporność dla wszystkich częstotliwości składowych i ewentualnie przeprowadzać dalsze obliczenia, które oczywiście pokazałyby, że przebieg prądu poważnie różni się kształtem od przebiegu napięcia. Miałoby to jakiś sens, ale byłoby niewyobrażalnie żmudne – w praktyce nie robimy takich operacji. Jednak nie byłoby to obliczanie reaktancji dla przebiegu innego niż sinusoidalny, bo nie ma czegoś takiego, jak reaktancja dla przebiegów odkształconych . Zawsze reaktancję kondensatora określamy dla „pojedynczego” przebiegu sinusoidalnego o jednej częstotliwości.

A tak na marginesie: procedura polegająca na rozkładaniu przebiegu na poszczególne harmoniczne, obliczeniach i składaniu harmonicznych dałaby identyczny kształt przebiegu, jak znacznie prostsze obliczenia wykorzystujące różniczkowanie i fakt, że prąd jest wprost proporcjonalny do zmian napięcia (I = du/dt).

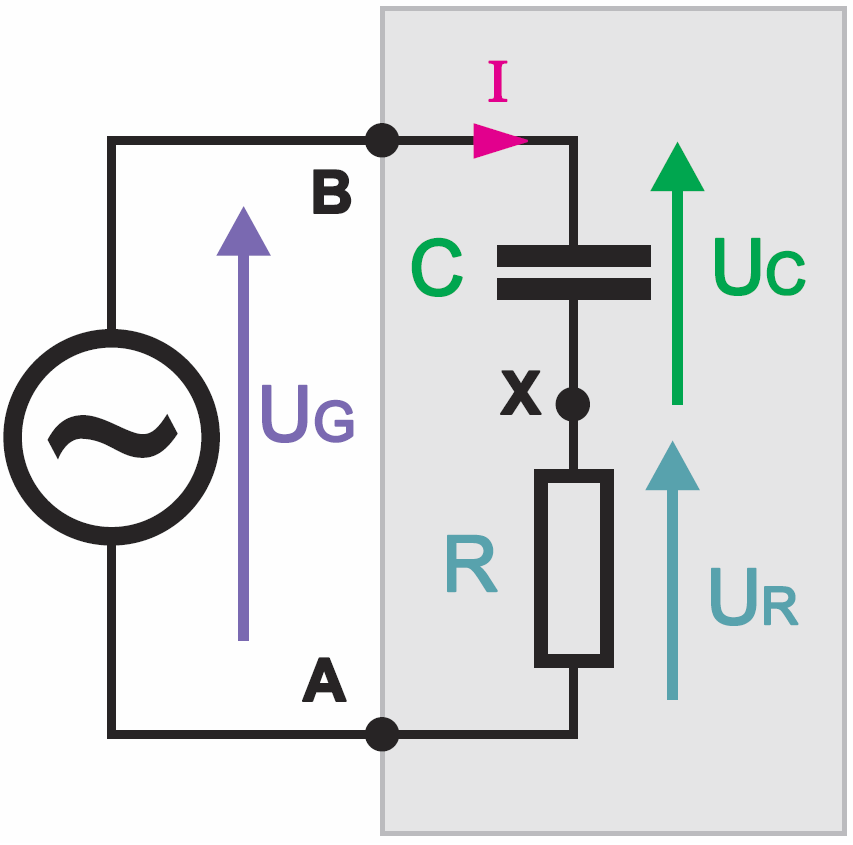
Drugi problem ze wzorem X_c = 1/2πfC polega na tym, że w naszych dotychczasowych rozważaniach lekkomyślnie pominęliśmy przesunięcie między prądem a napięciem. W przypadku „czystej reaktancji pojemnościowej” wszystko pasuje i wynik jest prawidłowy. Ale jak przeprowadzić obliczenia, gdy oporność nie jest ani czystą rezystancją, ani czystą reaktancją? Oto przykład: mamy szeregowe połączenie rezystora o oporności R i kondensatora o pojemności C, które będą pracować w układzie, gdzie występuje przebieg sinusoidalny o częstotliwości f – rysunek 4.

Oto proste pytanie: czy potrafimy obliczyć wartość prądu I, znając wartości R, C oraz częstotliwość przebiegu i napięcie U_G, występujące między punktami A, B?

Owszem, możemy łatwo obliczyć reaktancję X_c = 1/2πfC, a intuicja podpowiada, że przy szeregowym połączeniu oporności składowe należy zsumować. Jeśli jednak dodamy liczbowe wartości R+X_c i podstawimy do wzoru I = U/(R+X_c), to wynik takich obliczeń nie będzie zgodny z rzeczywistością… Gdyby na przykład obliczona wartość X_c była akurat liczbowo równa wartości R, wtedy błąd obliczeń wyniósłby ponad 40%.

Nie! Nie obawiaj się! Prawo Ohma nadal obowiązuje i podane wcześniej wzory są prawidłowe. Jednak my nie uwzględniliśmy przesunięcia fazowego między prądem i napięciem w kondensatorze i to dlatego wynik jest nieprawidłowy.

Czy masz jakiś pomysł, żeby uwzględnić przesunięcie fazowe w obliczeniach? Nie masz?

Nie dziwię się ani trochę, ponieważ właśnie doszliśmy do zagadnień, które dla wielu elektroników, i to nie tylko młodych, okazują się barierą nie do pokonania. A brak zrozumienia tych zagadnień powoduje, że poruszają się oni w elektronice niejako po omacku.

My spróbujemy tę barierę pokonać i to w miarę bezboleśnie. Złapmy więc byka za rogi. Po pierwsze, wyjaśnijmy sprawę przesunięcia fazowego, a w drugim kroku przejdziemy do obliczeń matematycznych.

Oporność zespolona – impedancja

Błędem, jaki popełniliśmy przy próbie obliczenia oporności wypadkowej, było bezpośrednie dodanie obliczonych liczbowych wartości X_c i rezystancji R. Owszem, elementy są połączone szeregowo i ich oporność wypadkowa rzeczywiście jest sumą X_c oraz R, ale nie można ich dodawać wprost.

Być może intuicja podpowiada Ci, że obliczona wartość X_c to jakieś „dziwne omy” – „omy pojemnościowe”. W takiej idei jest ziarno prawdy. Ale wyobrażenie, że chodzi o jakieś „dziwne omy” czy „inne omy” to ślepa uliczka. Nigdy tak nie myśl. Prawdą jest natomiast, że X_c to „dziwna oporność”, inna niż rezystancja, ponieważ mamy do czynienia z przesunięciem fazowym między prądem a napięciem, a tak w ogóle, to ta oporność ma sens tylko w przypadku przebiegów sinusoidalnych.

Przyjrzyjmy się bliżej oporności kondensatora. Wcześniejsze rysunki: 5, 6, 7 w tym wykładzie oraz rysunek 5 wskazują, że w kondensatorze przesunięcie między prądem a napięciem zawsze wynosi dokładnie jedną czwartą okresu (90°, czyli π/2).

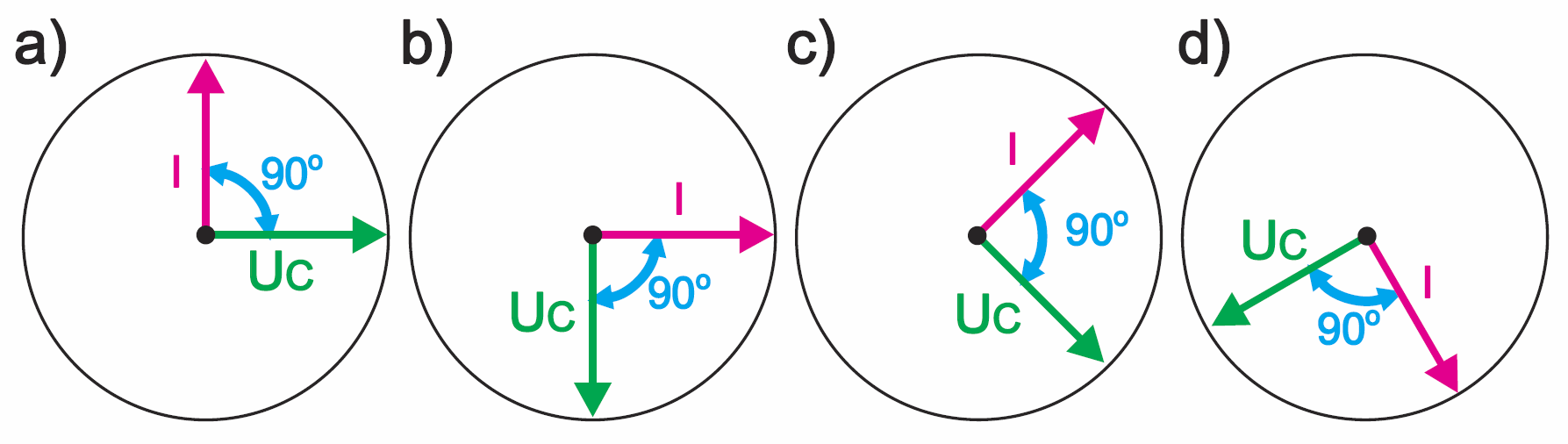
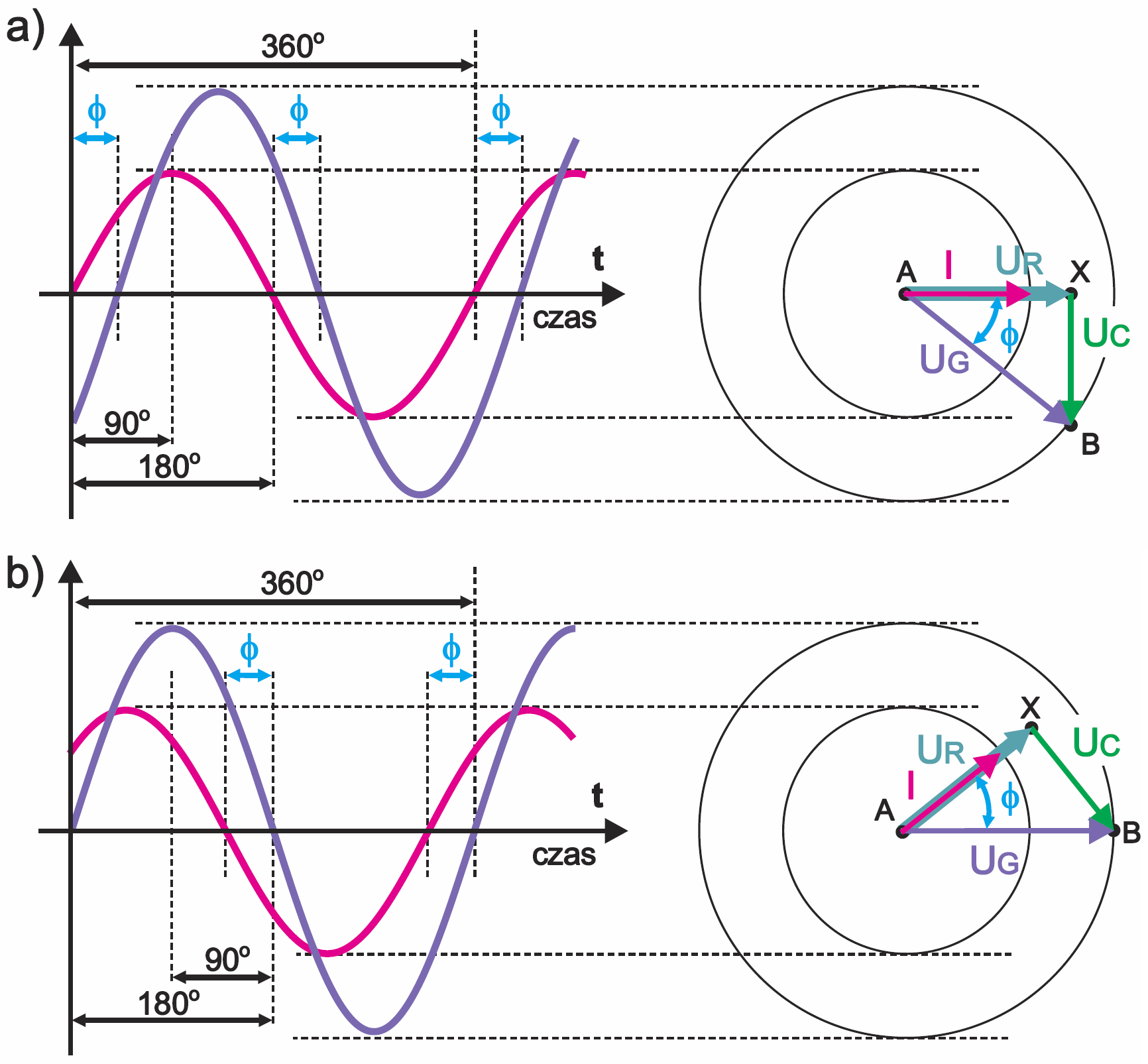
Zgodnie z informacjami z ostatnich dwóch odcinków, moglibyśmy przedstawić przesunięcie pomiędzy prądem a napięciem w postaci wektorów. Mogłoby to wyglądać jak na rysunku 6a, ale można też narysować tę zależność jak na rysunku 6b. Zwróć uwagę, że wszystkie cztery wersje z rysunku 6 prawidłowo pokazują przesunięcie między prądem a napięciem.

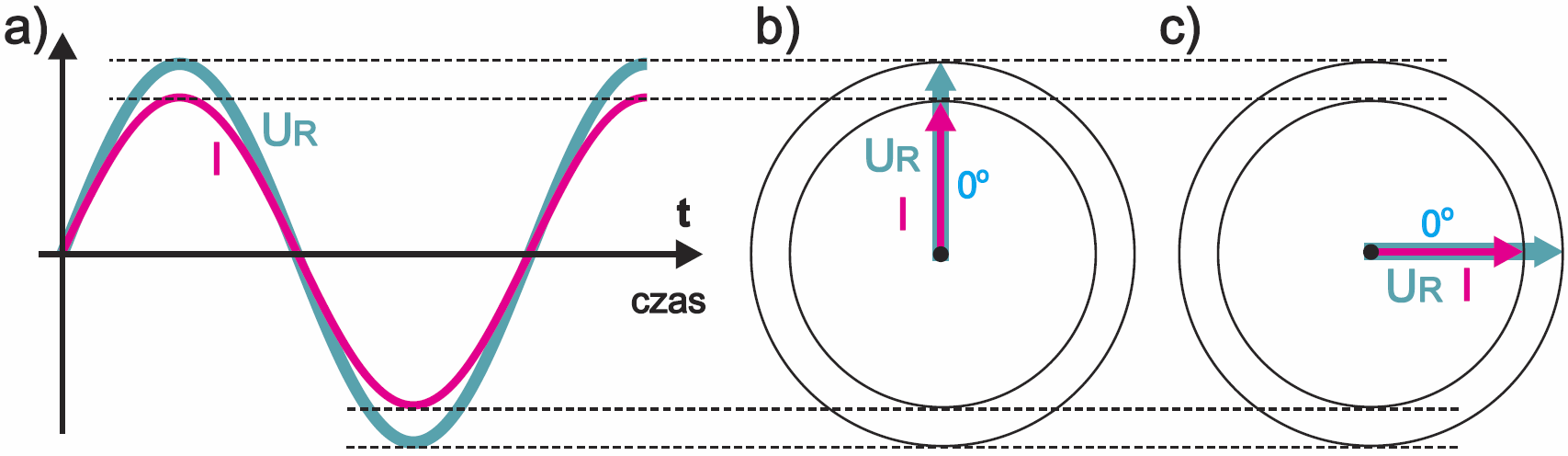
Natomiast w przypadku rezystora nie ma żadnego przesunięcia, wektory się nakładają i analogiczny wykres wygląda jak na rysunku 7. Popatrz sobie przez jakiś czas na dwa ostatnie rysunki…

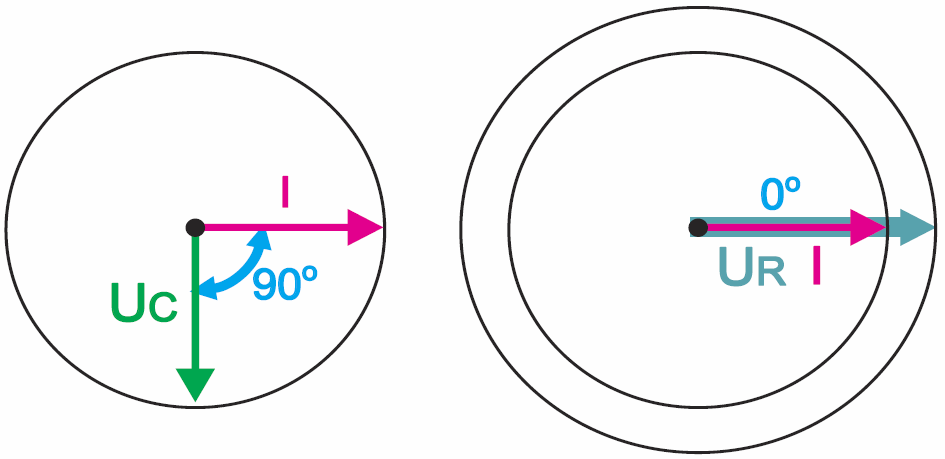
Zielonkawe strzałki reprezentują napięcie, czerwone prąd. Zauważ, że w obwodzie RC z rysunku 4 przez oba elementy płynie ten sam prąd I, a napięcie U_G niewątpliwie jest sumą napięć U_C+U_R. Zestawmy więc najpierw rysunki 6b i 7c, jak na rysunku 8.

W następnym kroku, na jednym wykresie możemy zaznaczyć ten wspólny prąd i dwa napięcia. Moglibyśmy narysować wykres jak na rysunku 9, jednak niewiele wnosi on do naszego rozumowania.

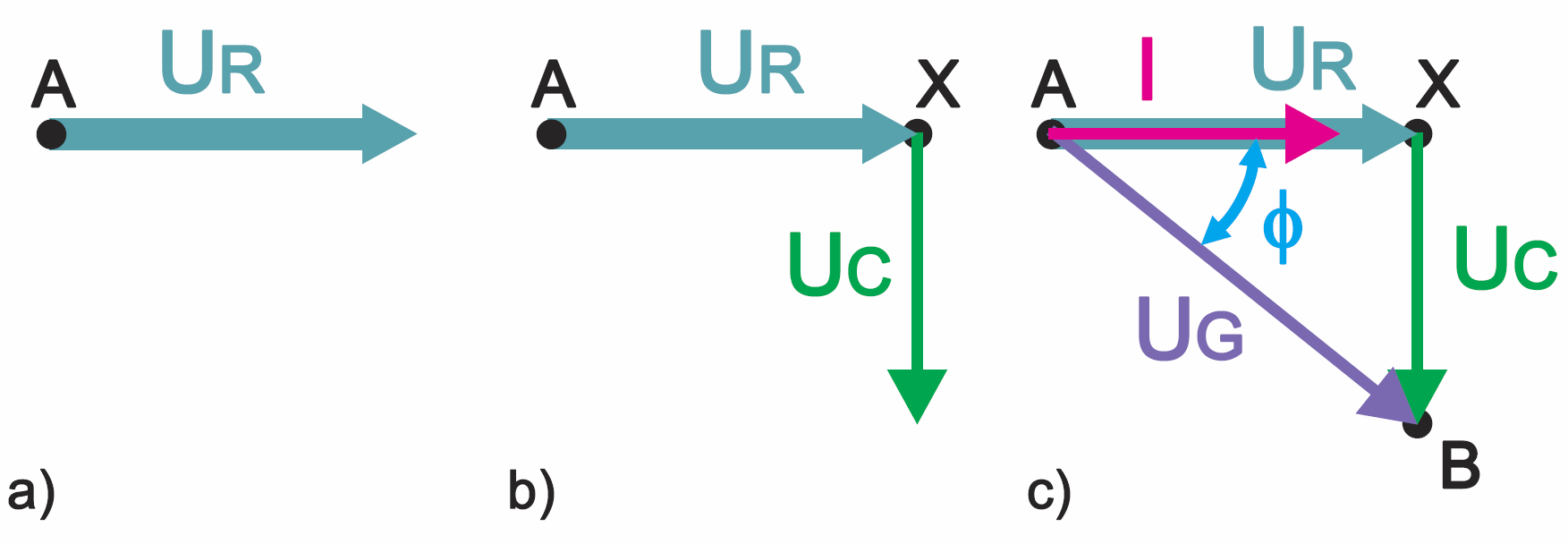
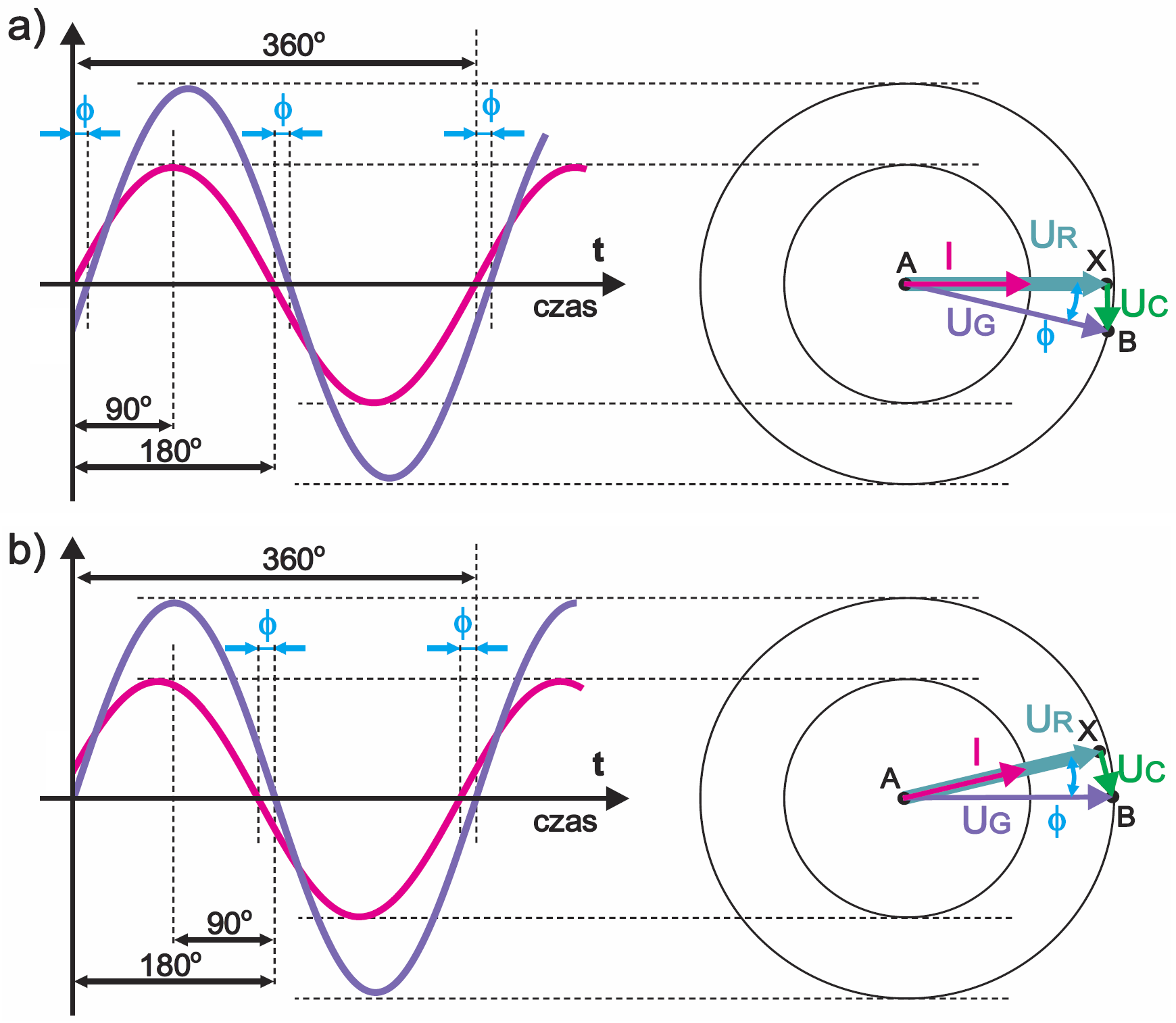
Zauważ jednak, że zgodnie z rysunkiem 4, napięcie U_G niewątpliwie jest sumą napięć na rezystorze i kondensatorze: U_G= U_R+U_C. Korzystając z rysunku 9, dodajmy więc w sposób graficzny wektory obrazujące te napięcia. Między punktami A, X występuje napięcie U_R – zgodnie z rysunkami 7, 8 zaznaczamy je na rysunku 10a. Między punktami X, B występuje napięcie U_C – zaznaczamy je, a właściwie dodajemy, zgodnie z rysunkami 6b, 8 – patrz rysunek 10b. Wszystko wskazuje, że napięcie U_AB należałoby zaznaczyć wektorem jak na rysunku 10c. Dziwne? I co to znaczy? Co to za kąt φ?

Dziwne tylko na pozór. Rysunek 10c wskazuje po prostu, że prąd I i napięcie U_G w naszym obwodzie RC są wzajemnie przesunięte właśnie o kąt φ. Możemy to narysować w postaci jak na rysunku 11a. Ale można też narysować tę samą sytuację nieco inaczej, jak na rysunku 11b – nie zmienia to istoty sprawy. Oba rysunki są prawidłowe.

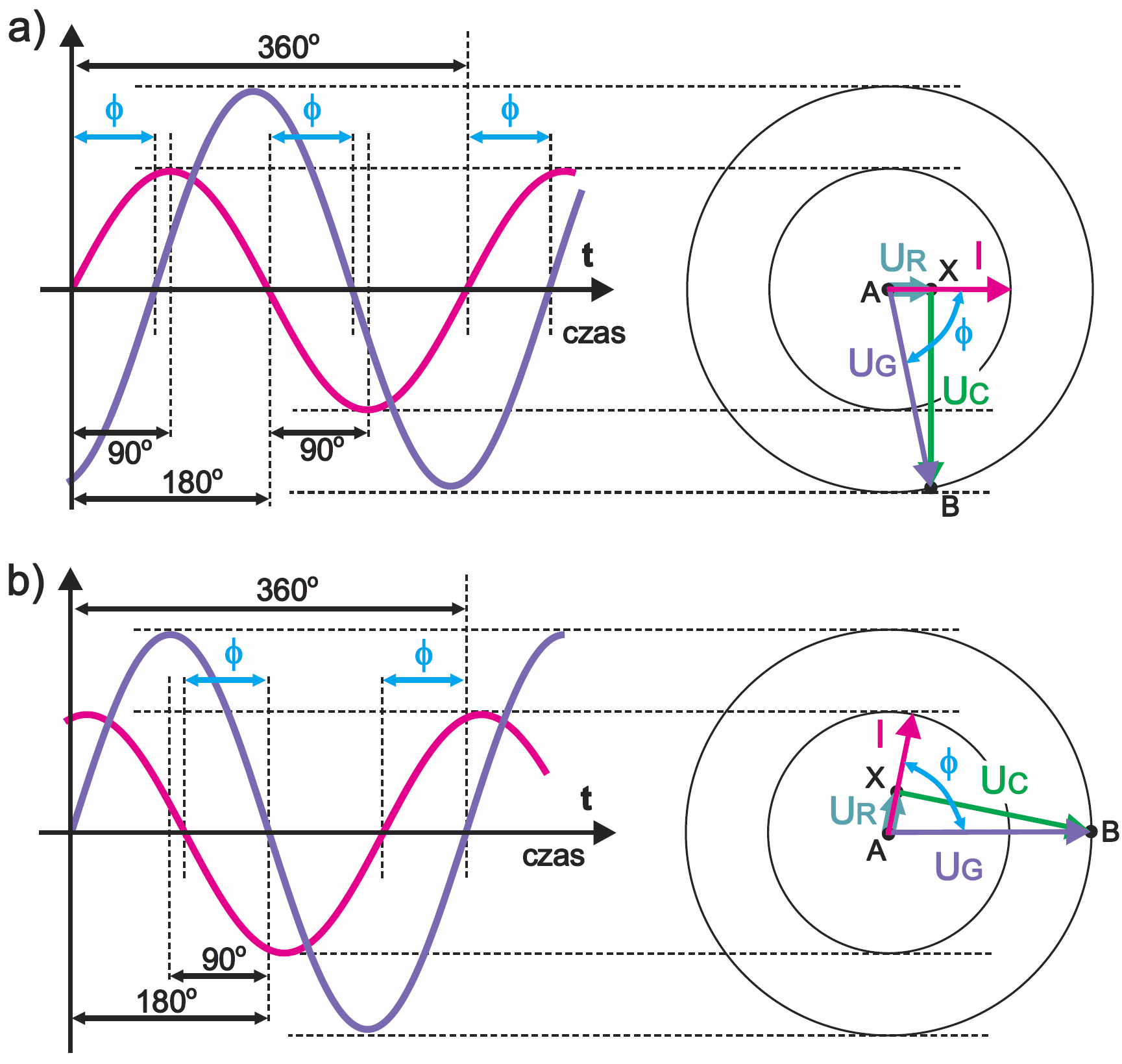
W omówionym właśnie przykładzie wartości napięć U_R, U_C były zbliżone, przez co kąt φ był nieco mniejszy niż 45 stopni. Gdyby jednak oporność X_c była dużo większa od R, wtedy zgodnie z prawem Ohma napięcie U_C też byłoby dużo większe od U_R. Sytuacja mogłaby wyglądać jak na rysunku 12.

Jeśli z kolei oporność R byłaby dużo większa od X_c, to sytuacja wyglądałaby jak na rysunku 13.

O ile dla „czystej reaktancji” X_c kąt przesunięcia zawsze wynosi 90 stopni, o tyle rysunki 11…13 wykazują, że blok będący złożeniem R i C wprowadza przesunięcie o wartości w zakresie między 0 a 90 stopni. Do tych szczegółów jeszcze powrócimy.

W następnym odcinku odcinku zrobimy ogromnie ważny krok – przedstawimy w postaci wektorów nie tylko prądy i napięcia, ale też oporności R oraz X_c!

Piotr Górecki