Elektronika (nie tylko) dla informatyków (12) Kondensator jako źródło energii

W ostatnim wykładzie zajmowaliśmy się zagadnieniami matematycznymi związanymi ze specyficznymi właściwościami kondensatorów i ich oporności. Wracajmy pomału do praktyki.

Przypomnijmy, że podstawową jednostką pojemności elektrycznej jest farad (F). W praktyce bardzo często wykorzystujemy jednostki podkrotne:
1 uF = 1 μF = 0,000 001 F
1 nF = 0,000 000 001 F
1 pF = 0,000 000 000 001 F

Unikamy podawania pojemności w milifaradach (1 mF = 0,001 F = 1000 μF), ponieważ w komputerach często mała literka mi (μ) z czcionki Symbol, zamienia się w literkę m, co prowadzi do błędów i nieporozumień. Dlatego też najlepiej jest w ogóle nie stosować greckiej literki mi (μ) i zamiast niej wykorzystywać podobną nieco z wyglądu zwykłą małą literę u. W związku z tym zamiast 2,2 mF piszemy 2200 uF, a zamiast 0,1 mF piszemy 100 uF. A teraz pora wracać do praktycznych zadań i właściwości spotykanych w praktyce kondensatorów.

Dla każdego coś miłego

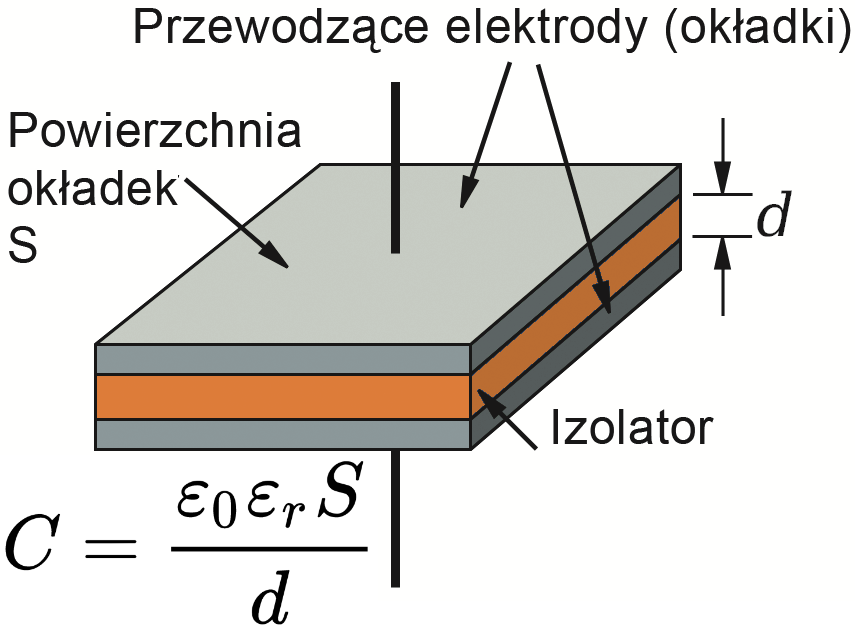
W szkolnych podręcznikach wszystko wygląda pięknie. Tam przedstawia się kondensator jako dwie metalowe płyty przedzielone warstwą izolatora i podaje się wzory na pojemność – patrz przykład na rysunku 1. W praktyce okazuje się, że taki kondensator ma żałośnie małą pojemność rzędu pikofaradów. Możesz zresztą sam to policzyć na podstawie podręcznikowych wzorów, albo też zmierzyć, jeżeli masz miernik z funkcją pomiaru pojemności od 1 pF.

Tymczasem w elektronice powszechnie stosowane są kondensatory elektrolityczne o nieporównanie większych pojemnościach od 1 mikrofarada do ponad 10000 mikrofaradów – fotografia 2.

Z drugiej strony, w niektórych przypadkach potrzebne są pojemności rzędu pojedynczych pikofaradów i wtedy kondensatorem (o regulowanej pojemności) mogą być choćby dwa kawałki izolowanego przewodu, jak na fotografii 3.

W sumie w naszej codziennej praktyce mamy do czynienia z kondensatorami o pojemności od jednego pikofarada (1 pF), co jest znikomą pojemnością (1 pF = 0,000 000 000 001 F). Z drugiej strony powszechnie wykorzystujemy kondensatory o pojemnościach miliardy razy większych, na przykład kondensatory elektrolityczne o pojemności rzędu dziesięciu tysięcy mikrofaradów (10 000 uF). 10 000 uF = 0,01 F = 10 000 000 000 pF

Istnieją też tak zwane ultrakondensatory o pojemnościach wielu faradów – fotografia 4 przedstawia ultrakondensatory koreańskiej firmy Vina (vina.co.kr), z których największe mają pojemność 680 faradów (tak!).

Natomiast fotografia 5 pokazuje wnętrze zasilacza UPS, gdzie 14 ultrakondensatorów o sumarycznej pojemności 4900 faradów (14×350 F) z powodzeniem zastępuje akumulator żelowy.

Wprawdzie ultrakondensatory, jak na razie, są wykorzystywane stosunkowo rzadko, ale jak by nie było, w elektronice mamy do czynienia z kondensatorami o pojemnościach różniących się kilkaset bilionów razy! Informacja o tak szerokim zakresie pojemności kondensatorów od 1 pikofarada do prawie tysiąca faradów, może budzić oszołomienie. Pomału spróbujemy to wszystko uporządkować. Zacznijmy od tego, że każdy kondensator i gromadzi energię, i jednocześnie ma jakąś reaktancję X_C w danych warunkach pracy. Jednak często możemy powiedzieć, że dany kondensator pracuje tylko w jednej roli, a druga nas nie interesuje. Te dwa główne powody to:
– praca w roli filtrów,
– gromadzenie energii.

Kondensator jako źródło energii

Jak już wiesz, kondensator może gromadzić energię i w niektórych zastosowaniach pełni rolę pomocniczego źródła zasilania. Tak jest we wszelkich zasilaczach, gdzie kondensatory dużej pojemności są ładowane impulsami prądowymi, a w czasie pomiędzy tymi impulsami kondensatory są źródłem energii. I tu mamy pierwszy główny powód wykorzystywania kondensatorów w układach elektronicznych – gromadzenie energii. Wtedy zazwyczaj nie interesuje nas reaktancja. Łatwo można byłoby obliczyć, że np. pracujący w zasilaczu kondensator filtrujący o pojemności, powiedzmy 10 000 uF (0,01 F), przy częstotliwości 50 Hz ma reaktancję:
X_C = 1/(2π×50 Hz×0,01 F)
X_C = 0,159/(50 Hz×0,01 F)
X_C = 0,318 Ω

Jednak taka informacja jest praktycznie bezużyteczna, i to z kilku powodów. Zwłaszcza w przypadku jeszcze większych pojemności.

Otóż takie same obliczenia dla ultrakondensatora o pojemności 350 F (fotografie 3, 4):

X_C = 1/(2π×50 Hz×350 F)
X_C = 0,000009 Ω = 0,009 mΩ

dają wynik budzący wątpliwości każdego praktyka, który wie, że nawet króciutki kawałek drutu ma oporność rzędu co najmniej pojedynczych miliomów. Rzeczywiście, w praktyce oprócz reaktancji X_C w grę wchodzą też inne ważne czynniki i parametry, zazwyczaj szkodliwe, które mają wpływ na działanie układów elektronicznych. Zajmiemy się tym w najbliższych odcinkach.

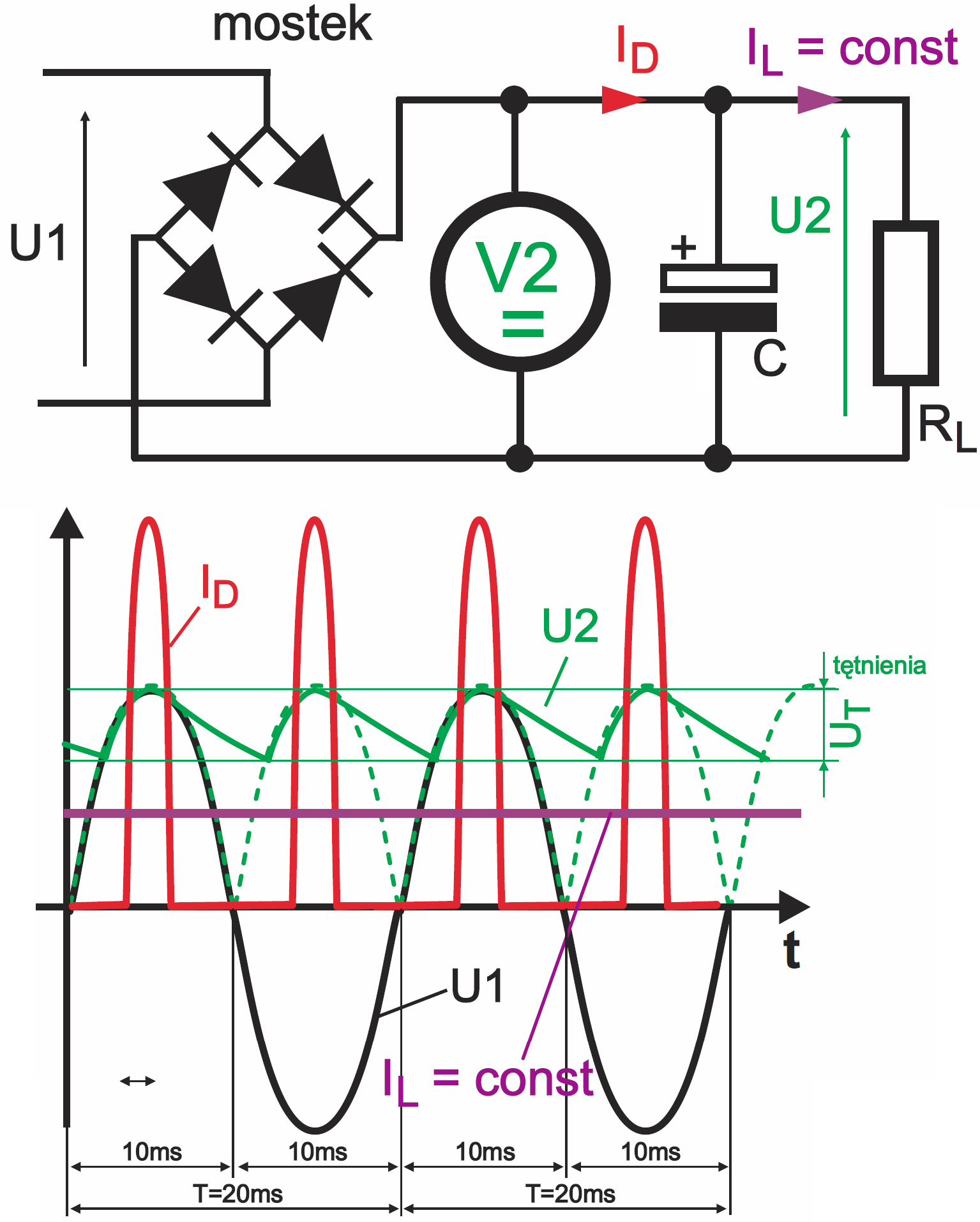
A na razie możesz przyjąć w uproszczeniu, że kondensatory o pojemności co najmniej 100 mikrofaradów (100 uF) pełnią w układach rolę pomocniczych źródeł energii, czyli są jakby maleńkimi akumulatorkami i w takich zastosowaniach nie interesuje nas ich reaktancja pojemnościowa X_C. Co ciekawe, w praktyce prawie nigdy nie przeprowadzamy też obliczeń dotyczących ilości gromadzonej energii (E=CU²/2). Aby dobrać pojemność kondensatora w zasilaczu, zazwyczaj nie przeprowadzamy ścisłej analizy, tylko korzystamy z podstawowej zależności C × ΔU = I × Δt, którą to zapisujemy w uproszczeniu CU = It. Jeżeli mamy policzyć potrzebną pojemność, korzystamy z przekształconego wzoru: C = It / U gdzie I – pobór prądu, t – czas między impulsami ładującymi, a w praktyce okres tych impulsów, U – (ściślej ΔU) dopuszczalne zmiana napięcia podczas okresu, czyli inaczej tętnienia. Przykładowo dla zasilacza sieciowego (50 Hz) z prostownikiem mostkowym według rysunku 6 czas t wynosi 10 ms, ponieważ kondensator ładowany jest dwukrotnie w ciągu każdego okresu sieci 50 Hz. Jeśli pobór prądu (I_L) ma wynosić 1 A i jeśli maksymalne tętnienia (U_T) nie mogą być większe od 1 V (ich międzyszczytowa amplituda), to kondensator filtrujący nie powinien mieć pojemności mniejszej niż:

C = 1 A×10 ms / 1 V = 10 mF = 10000 uF

Podobnie z zależności CU = It możemy na przykład obliczyć, jak zmieniać się będzie napięcie na zestawie kondensatorów UPS-a z fotografii 5, gdzie sumaryczna pojemność wynosi 4900 faradów. Załóżmy, że z tego zestawu przez 1 minutę (60 s) pobierany jest prąd 10 A. Przekształcony wzór ma w tym wypadku postać:
U = It/C
U = 10 A×60 s/4900 F = 600 As/4900 F
U = 0,122 V

A więc przy tej pojemności, nawet przepływ potężnego prądu 10 A przez 60 sekund spowoduje obniżenie napięcia tylko o 122 mV!

Podsumujmy: w przypadku kondensatorów pracujących jako źródła energii, korzystamy jedynie z zależności CU = It nie wgłębiamy się w dalsze szczegóły.

W następnym wykładzie zajmiemy się kondensatorami pracującymi w roli filtrów.

Piotr Górecki