Elektronika (nie tylko) dla informatyków (20) Obwód LC – drgania swobodne

W poprzednim odcinku przybliżyliśmy pojęcie reaktancji indukcyjnej. W tym wykładzie zajmiemy się właściwościami obwodu LC.

Obwód LC – drgania swobodne

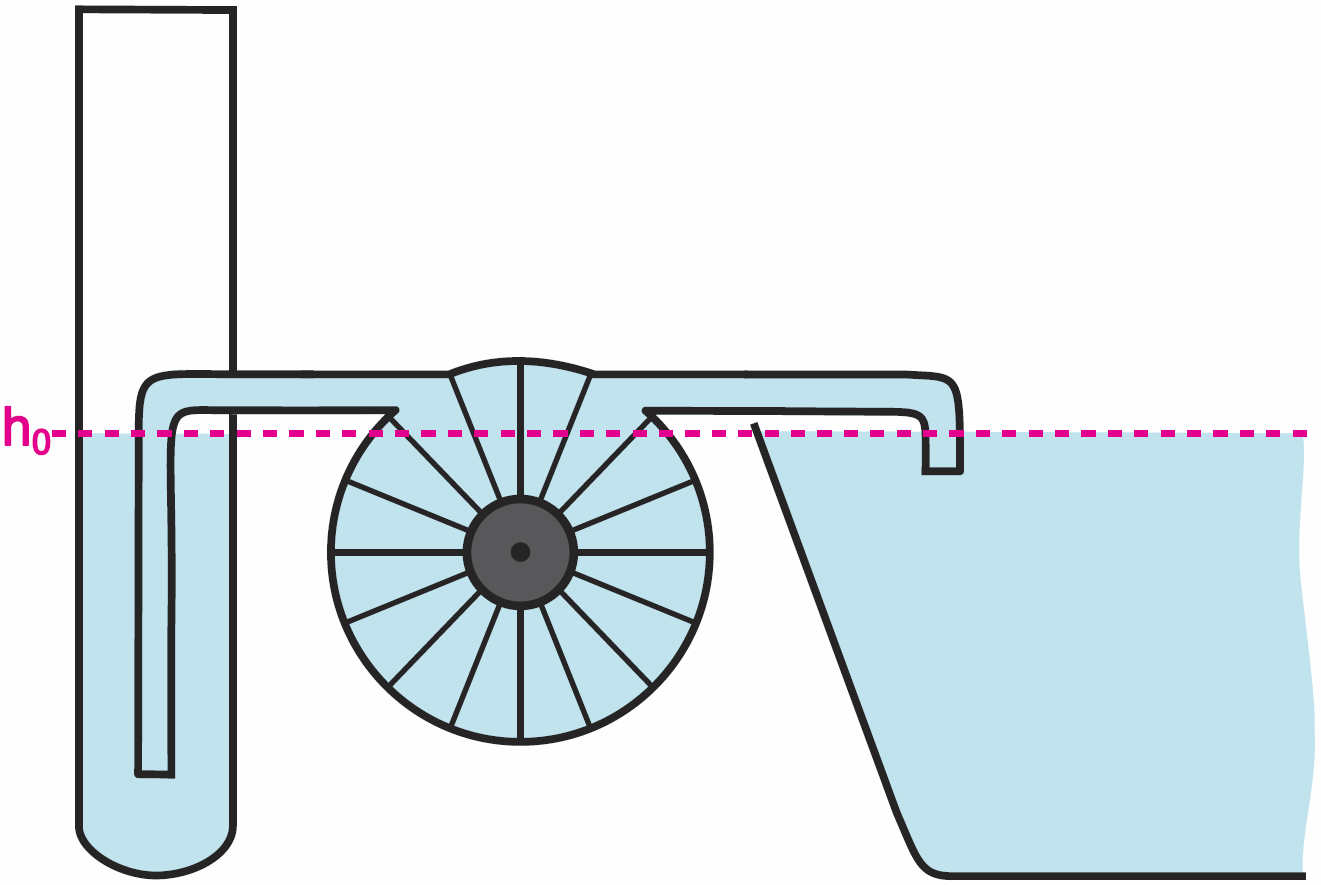
Omawianie obwodów LC zacznijmy od analogii hydraulicznej z rysunku 1. Mamy tu połączenie cewki-turbiny oraz kondensatora-rury, a system połączony jest z dużym zbiornikiem wodnym, na przykład z dużym jeziorem.

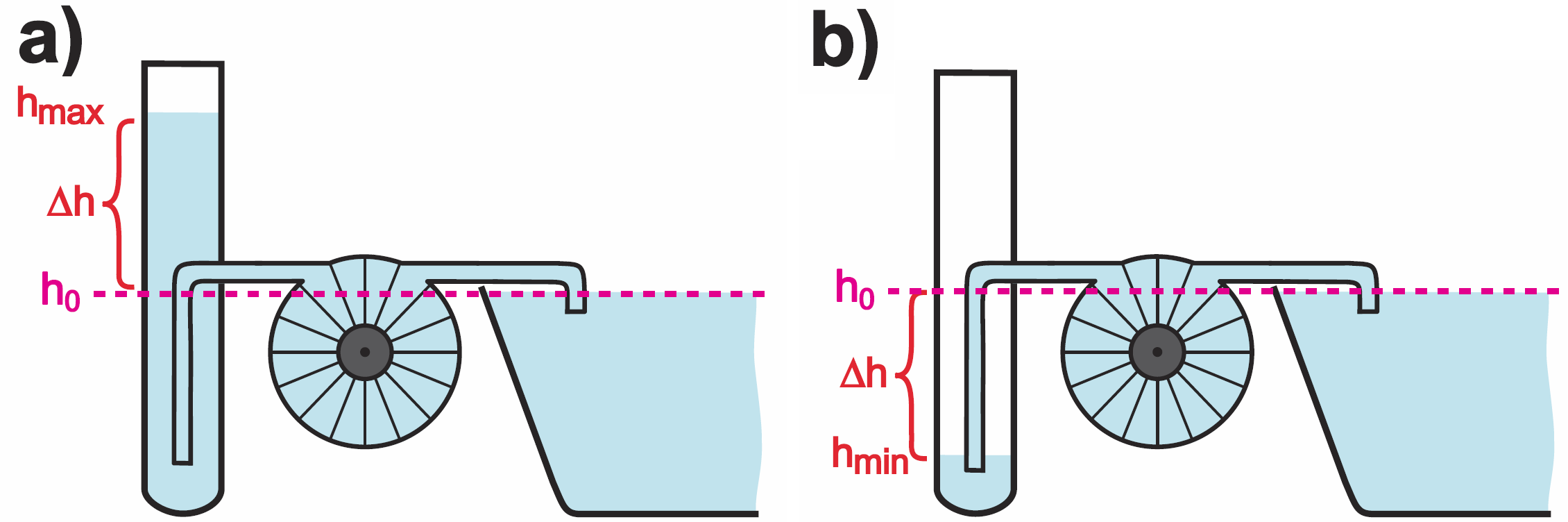
Kondensator-rura ma nieco inną postać, niż na wcześniejszych rysunkach, ponieważ będziemy mieć do czynienia z przebiegiem zmiennym, co jednak ani trochę nie zmienia zasady działania. Sytuacja z rysunku 1 to stan spoczynkowy, gdy w układzie nic się nie dzieje. Załóżmy jednak, że nalejemy wody do rury (naładujemy kondensator) i w pewnej chwili sytuacja wygląda jak na rysunku 2a: poziom wody w rurze-kondensatorze jest znacznie wyższy niż poziom wody w jeziorze (h_max), a turbina jest nieruchoma. Słup wody o wysokości Δh wytwarza pewne ciśnienie, więc turbina zacznie się obracać i nabierać prędkości. Gdy poziom wody w rurze-kondensatorze spadnie do poziomu jeziora (h₀), wtedy ciśnienie wywierane przez słup wody spadnie do zera, ale woda będzie przepływać nadal, a to z uwagi na to, że turbina-cewka zdążyła nabrać obrotów i jej bezwładność powoduje, że będzie obracać się nadal. Można powiedzieć, że energia potencjalna wody zamieniła się w energię kinetyczną turbiny. Dlatego od chwili, gdy poziom wody w rurze spadnie do zera, turbina zacznie działać jako pompa i będzie wypompowywać wodę z rury. Wprawdzie turbina będzie się obracać coraz wolniej, jednak zdąży wypompowywać sporo wody z rury. Jeśliby w takim systemie nie było żadnych strat, to poziom wody opadłby do poziomu h_min, o dokładnie taką samą odległość Δh poniżej poziomu zerowego, jak w przypadku poziomu maksymalnego – rysunek 2b. Oczywiście potem turbina zaczęłaby się coraz szybciej obracać w przeciwną stronę i poziom wody w rurze zacząłby się podnosić. Najpierw wzrósłby do poziomu h₀, i wtedy turbina osiągnęłaby maksymalną prędkość, a potem rozpędzona turbina wpompowałaby wodę do rury. Jeśli nie byłoby w tym systemie żadnych strat, poziom wody znów wzrósłby do wysokości h_max, a potem cykl powtarzałby się w nieskończoność. Poziom wody w rurze oraz prędkość turbiny zmieniałyby się w rytm przebiegu sinusoidalnego. Po jednorazowym „zasileniu” otrzymalibyśmy oscylator, generator przebiegu sinusoidalnego.

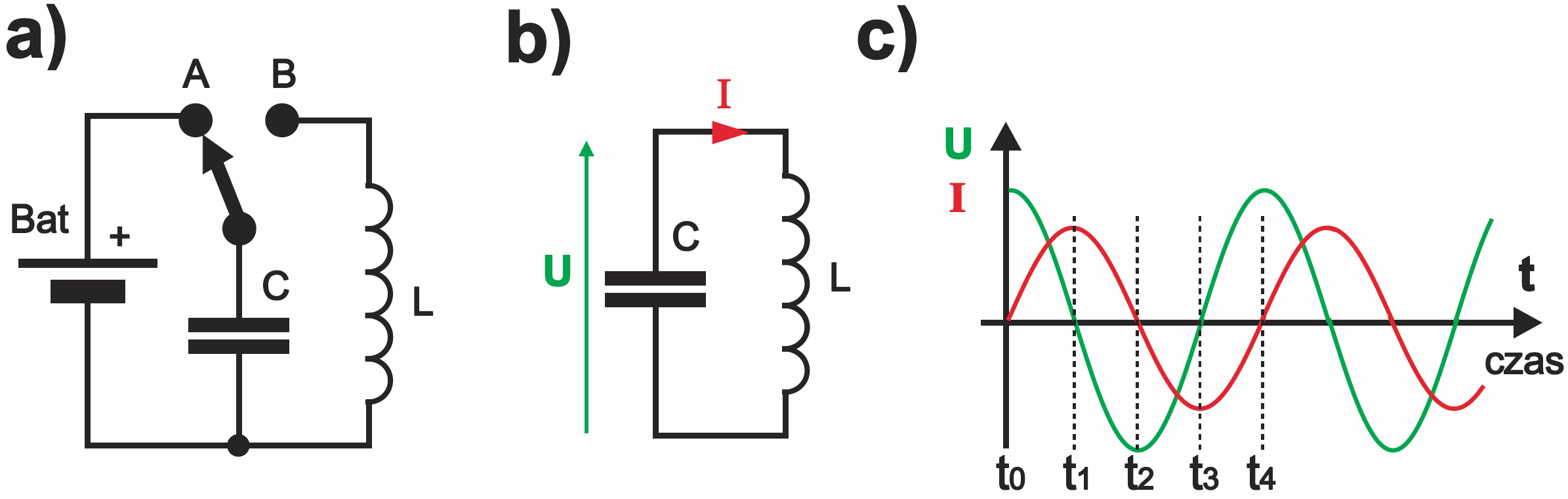
A teraz podobny układ elektryczny: najpierw w sytuacji z rysunku 3a gromadzimy energię (ładujemy kondensator z baterii Bat). Następnie po przełączeniu przełącznika w położenie B tworzymy obwód LC – rysunek 3b. W pierwszej chwili po przełączeniu kondensator jest naładowany, czyli zawiera jakąś porcję energii (E = CU²/2) i występuje na nim napięcie stałe (dodatnie) o wartości dokładnie takiej, jak napięcie baterii.

Na rysunku 3c jest to chwila t₀. W tej pierwszej chwili po przełączeniu prąd nie płynie, ale od chwili przełączenia kondensator ma możliwość rozładowania się i przez cewkę zaczyna płynąć prąd. Prąd ten przenosi do cewki energię zgromadzoną w kondensatorze. Zgodnie z zasadą działania cewki, płynący prąd zaczyna rosnąć. Prąd nie może jednak rosnąć nieograniczenie, ponieważ przepływ prądu jednocześnie oznacza stopniowe rozładowywanie kondensatora. Napięcie na kondensatorze zmniejsza się i prąd rośnie coraz wolniej. W chwili, gdy napięcie na kondensatorze spadnie do zera, prąd przestaje rosnąć. W tym właśnie momencie, na rysunku 3c oznaczonym t₁, napięcie na kondensatorze jest równe zeru, więc zgodnie ze wzorem E = CU²/2, jego energia jest równa zeru. Cała energia zgromadzona na początku w kondensatorze jest w tym momencie zawarta w cewce, przez którą płynie prąd (E = LI²/2). Zgodnie ze swoją zasadą działania, cewka „nie lubi zmian prądu”, dlatego prąd będzie płynął nadal w tym samym kierunku. A to oznacza, że cewka jako źródło energii zaczyna ładować kondensator. Cewka przekazuje swoją energię do kondensatora. Trzeba jednak zauważyć, że dalszy przepływ prądu w tym samym kierunku oznacza ładowanie kondensatora napięciem o biegunowości przeciwnej, niż było na początku. Na kondensatorze napięcie staje się więc coraz bardziej ujemne. Cewka oddaje energię do kondensatora i płynący prąd jest coraz mniejszy. Wreszcie w chwili oznaczonej t₂ prąd staje się równy zeru. Zgodnie ze wzorem E = LI²/2, energia zawarta w cewce jest równa zeru. Cała energia znów zawarta jest w kondensatorze, na którym występuje napięcie równe napięciu baterii, tylko ujemne. Znów kondensator staje się źródłem energii i przez cewkę zaczyna płynąć coraz większy prąd, tylko o kierunku odwrotnym, niż wcześniej. Napięcie na kondensatorze zmniejsza się, a prąd staje się coraz większy. W chwili t₃ napięcie na kondensatorze staje się równe zeru, a prąd w cewce osiąga maksymalną wartość – znów cała energia zgromadzona jest w cewce. Później cewka, która „nie lubi zmian prądu”, podtrzymuje przepływ prądu w tym samym „ujemnym” kierunku. Ten malejący prąd zaczyna ładować kondensator – energia znów jest przekazywana do kondensatora. Wreszcie w chwili t₄ cewka przekaże całą energię do kondensatora i sytuacja będzie dokładnie taka sama, jak w chwili t₀. Cykl będzie się powtarzał. Oczywiście gdyby kondensator i cewka były idealne, takie oscylacje utrzymałyby się wiecznie. Do takiego idealnego systemu wystarczyłoby jednorazowo dostarczyć porcję energii i energia ta przez wieczność krążyłaby na przemian między kondensatorem i cewką. Czy byłbyś skłonny stwierdzić, że taki obwód zamienia napięcie stałe na przebieg sinusoidalnie zmienny?

Oczywiście w praktycznych systemach i obwodach zawsze występują straty energii, choćby wskutek tarcia wody o ścianki rur w systemie hydraulicznym czy rezystancję drutu cewki indukcyjnej. Dlatego w rzeczywistości oscylacje nie będą się utrzymywać wiecznie. W każdym cyklu pracy tracona będzie część energii i drgania będą coraz mniejsze. Przebieg sinusoidalny będzie mniej lub bardziej tłumiony. Do tej ważnej sprawy jeszcze wrócimy, a na razie zajmijmy się inną ogromnie ważną kwestią. Chodzi o częstotliwość drgań takiego obwodu LC.

Częstotliwość drgań

Moglibyśmy próbować matematycznie wyprowadzić wzór na częstotliwość drgań obwodu z rysunku 3b. Jest to możliwe, ale trzeba byłoby wykorzystać wyższą matematykę (m.in. równania różniczkowe, ewentualnie transformatę Laplace’a oraz zmienną zespoloną s). My spróbujmy to zrobić w sposób bardzo uproszczony.

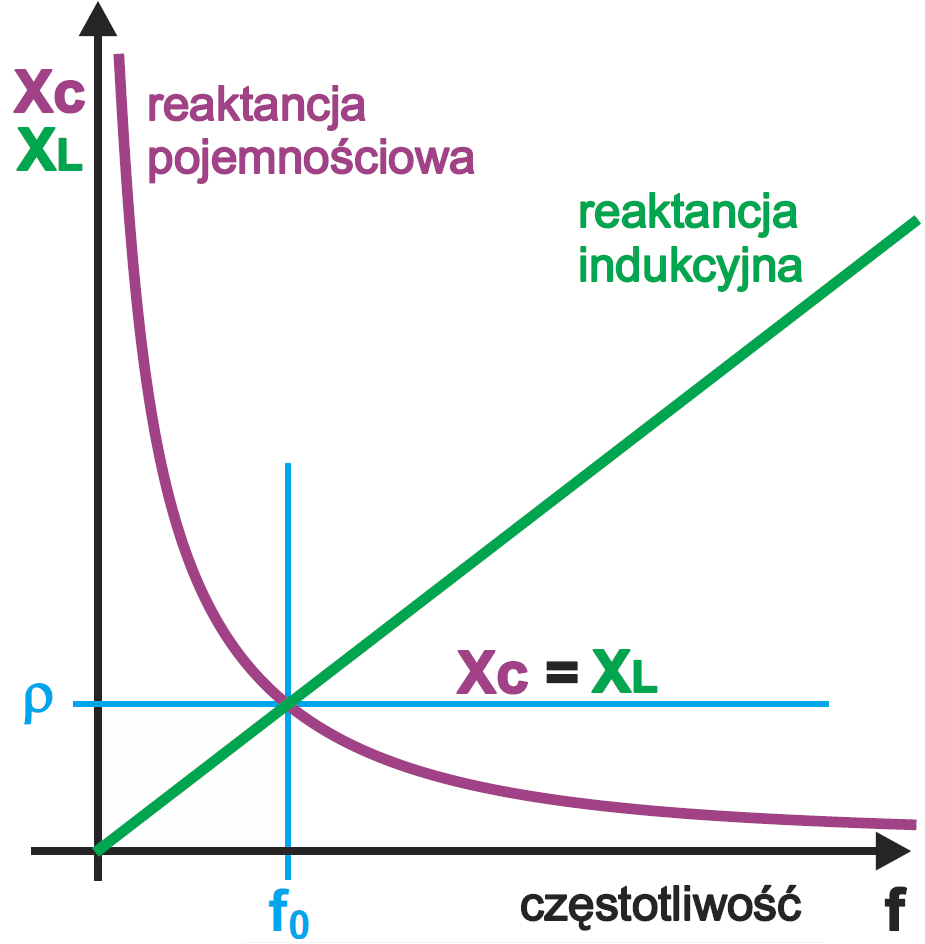
Otóż wiadomo, że reaktancja indukcyjna cewki X_L rośnie liniowo ze wzrostem częstotliwości (pulsacji) według zależności: X_L=2πfL=ωL

Z kolei reaktancja pojemnościowa X_C maleje ze wzrostem częstotliwości według wzoru: X_C= 1/2πfC=1/ωC

Ilustruje to rysunek 4.

Dla jakiejś częstotliwości f₀ reaktancja pojemnościowa i indukcyjna mają jednakowe wartości X_L=X_C, czyli 2πf₀L=1/2πf₀C

A jeśli tak, to przekształcamy:

(2πf₀L)(2πf₀C) = 1           2²π²f₀²LC = 1           f₀²= 1/2²π²LC           f₀=1/(2²π²LC)^1/2           f₀=1/2π(LC)^1/2

Co zapisujemy w bardziej znanej postaci:

W zasadzie obliczyliśmy tylko częstotliwość, przy której reaktancje indukcyjna i pojemnościowa mają tę samą wartość, ale przyjmij na wiarę, że jest to także częstotliwość drgań wytwarzanych w idealnym obwodzie LC z rysunku 3.

W podręcznikach częściej używa się pojęcia pulsacji, niż częstotliwości (ω=2πf), dlatego bardzo często spotykamy zapis:

Już jeden rzut oka na dwa ostatnie wzory prowadzi do wniosku, że daną częstotliwość (pulsację) można uzyskać przy nieskończenie wielkiej liczbie kombinacji wartości L, C, byle tylko iloczyn LC pozostał jednakowy (LC=const).

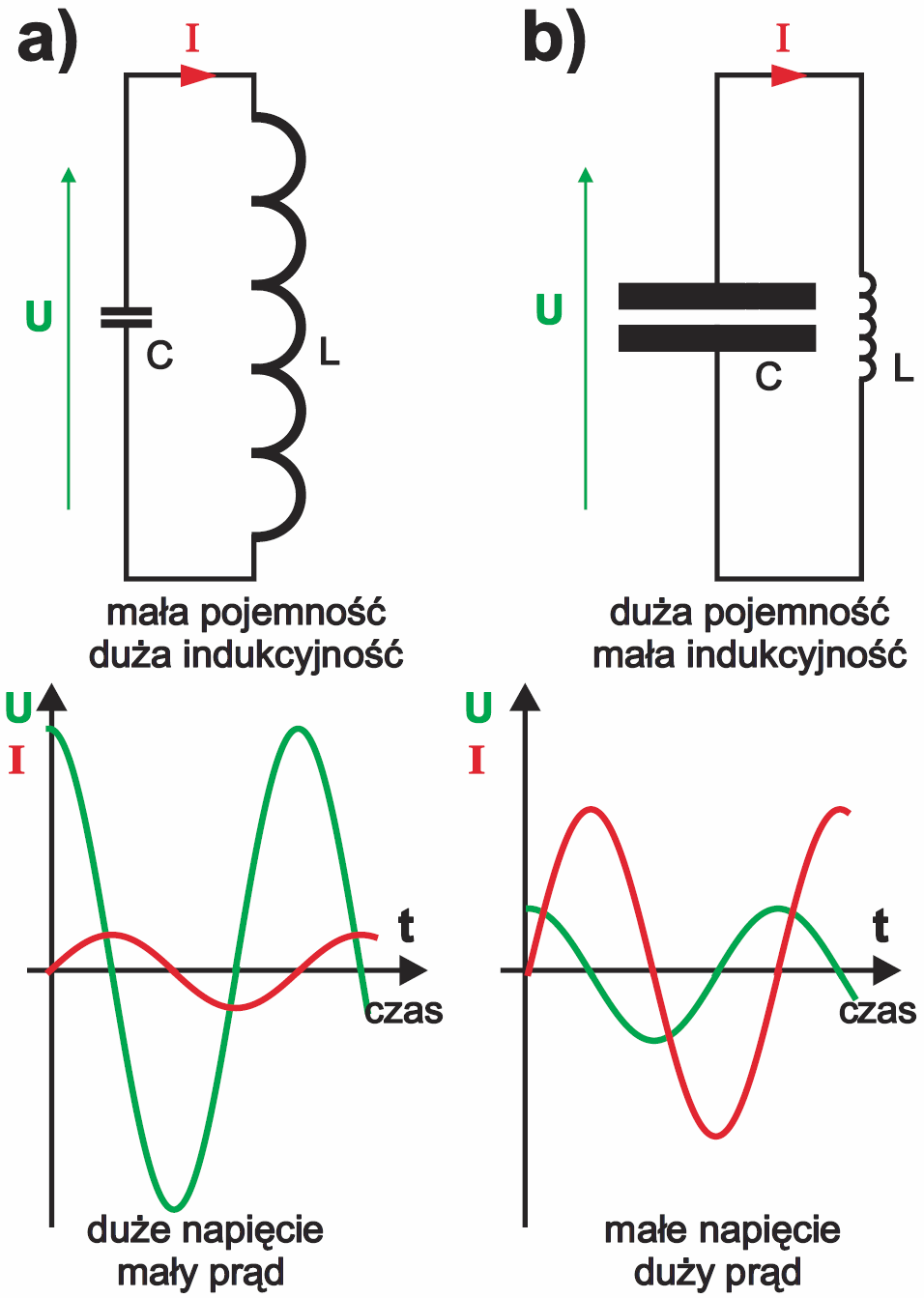
Ilustruje to także analogia hydrauliczna. Otóż daną częstotliwość oscylacji możemy uzyskać, stosując małą pojemność (cienką rurę) i dużą indukcyjność (masywne koło zamachowe). Możemy też wykorzystać dużą pojemność (rura o dużym przekroju) i małą indukcyjność (turbina o małej bezwładności i masie). Tak samo w obwodzie elektrycznym LC. Dwa takie przypadki zilustrowane są na rysunku 5. Oba obwody wytworzą oscylacje o tej samej częstotliwości. A jakie będą różnice?

Dla ułatwienia analizy załóżmy, że do obu systemów na początek dostarczamy jednakową porcję energii. A to oznacza, że aby w obwodzie z rysunku 5a z małym kondensatorem zgromadzić tę porcję energii, musimy go naładować do wysokiego napięcia. Natomiast ta sama porcja energii „wlana” do kondensatora o dużej pojemności oznacza niewielkie napięcie na kondensatorze. W obwodzie z rysunku 5a pomimo znacznego napięcia, zmiany prądu będą małe, ponieważ duża jest indukcyjność, która przeciwstawia się zmianom prądu. Zapamiętaj: wysokie napięcie i mały prąd.

Natomiast w obwodzie z rysunku 5b indukcyjność jest mała, więc nawet niezbyt duże napięcie z kondensatora spowoduje duże zmiany prądu. Notujemy: małe napięcie i duży prąd. Jeśli chcesz, samodzielnie przeanalizuj analogię hydrauliczną.

Jeszcze raz powtarzam: w obu obwodach powstaną oscylacje o identycznej częstotliwości. Różnica będzie taka, że w pierwszym napięcie będzie duże, a prąd mały, w drugim napięcie małe, a prąd duży.

Jeśli w pierwszym przypadku mamy duże napięcie i mały prąd, to intuicyjnie czujemy, że mamy do czynienia z dużą opornością. W drugim przypadku małe napięcie i duży prąd podpowiadają, że mamy do czynienia z małą opornością.

I słusznie! Zbadajmy tę kwestię nieco bliżej.

Oporność charakterystyczna

Przy częstotliwości drgań własnych f₀ cewka będzie miała oporność: X_L=2πf₀L=ω₀L

wcześniej stwierdziliśmy, że: ω₀=1/(LC)^1/2 teraz podstawmy ω₀ do pierwszego wzoru:

X_L = ω₀L = [1/(LC)^1/2]L = L/(LC)^1/2

X_L = (L²)^1/2/(LC)^1/2 = (L²/LC)^1/2 = (L/C)^1/2

X_L=(L/C)^1/2

Podobnie podstawmy ω₀=1/(LC)^1/2 do wzoru na X_C:

X_C = 1/ω₀C = 1/[1/(LC)^1/2]C = (LC)^1/2/C

X_C = (LC)^1/2/(C²)^1/2 = (LC/C²)^1/2

X_C=(L/C)^1/2

Zwróć uwagę, że wartości reaktancji przy częstotliwości drgań możemy obliczyć szybko bez obliczania częstotliwości, znając tylko L i C. Często oporność tę nazywany opornością charakterystyczną obwodu LC i oznaczamy małą grecką literką ro (ρ)

ρ = X_L=X_C=(L/C)^1/2 Częściej zapisujemy to w następującej postaci:

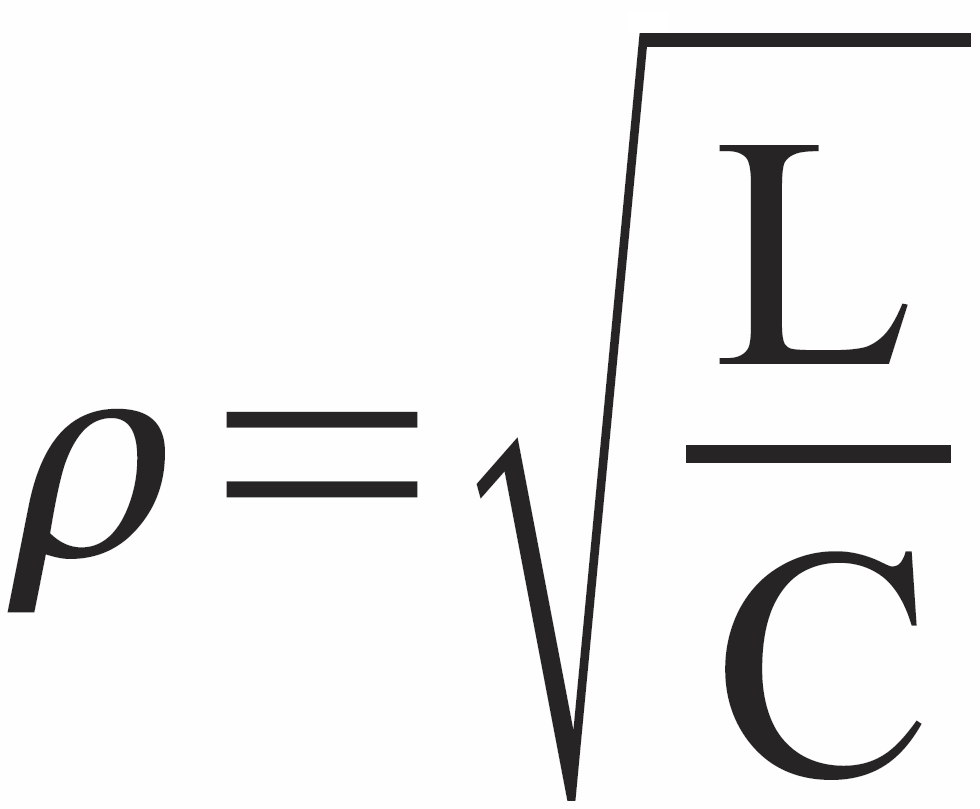
Oporność tę zaznaczyłem już wcześniej na rysunku 4.

Początkującym może się to wydać bardzo dziwne, ale bardziej dociekliwi Czytelnicy sprawdzą, że wymiarem henra jest V×s/A, czyli omosekunda, natomiast wymiarem farada jest A×s/V, czyli sekunda przez om i wszystko w powyższym wzorze się zgadza.

Zgadza się matematycznie, ale po co nam wartość tak obliczonej oporności charakterystycznej?

Otóż jest przydatna w praktyce, między innymi w związku z dobrocią.

Obwód RLC i jego dobroć

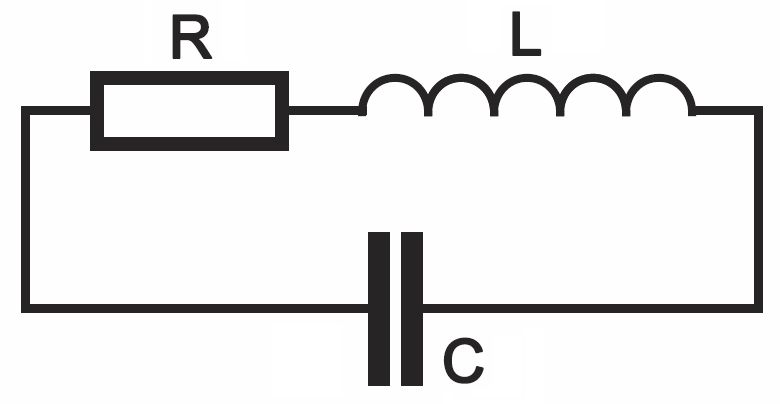
Do tej pory rozpatrywaliśmy idealny obwód LC, bez żadnych strat. Tymczasem w każdym rzeczywistym obwodzie LC występują straty i straty te reprezentowane są na schemacie przez rezystancję R. Rzeczywisty obwód LC możemy uważać za połączenie idealnego kondensatora C oraz idealnej cewki L i szeregowego rezystora R, jak pokazuje rysunek 6. Rezystancja R reprezentuje tu wszelkie straty, ale w pierwszym, zgrubnym przybliżeniu możemy sobie wyobrazić, że jest to rezystancja uzwojenia (drutu) cewki.

I teraz bardzo ważne pytanie: co zmienia w obwodzie obecność rezystancji R?

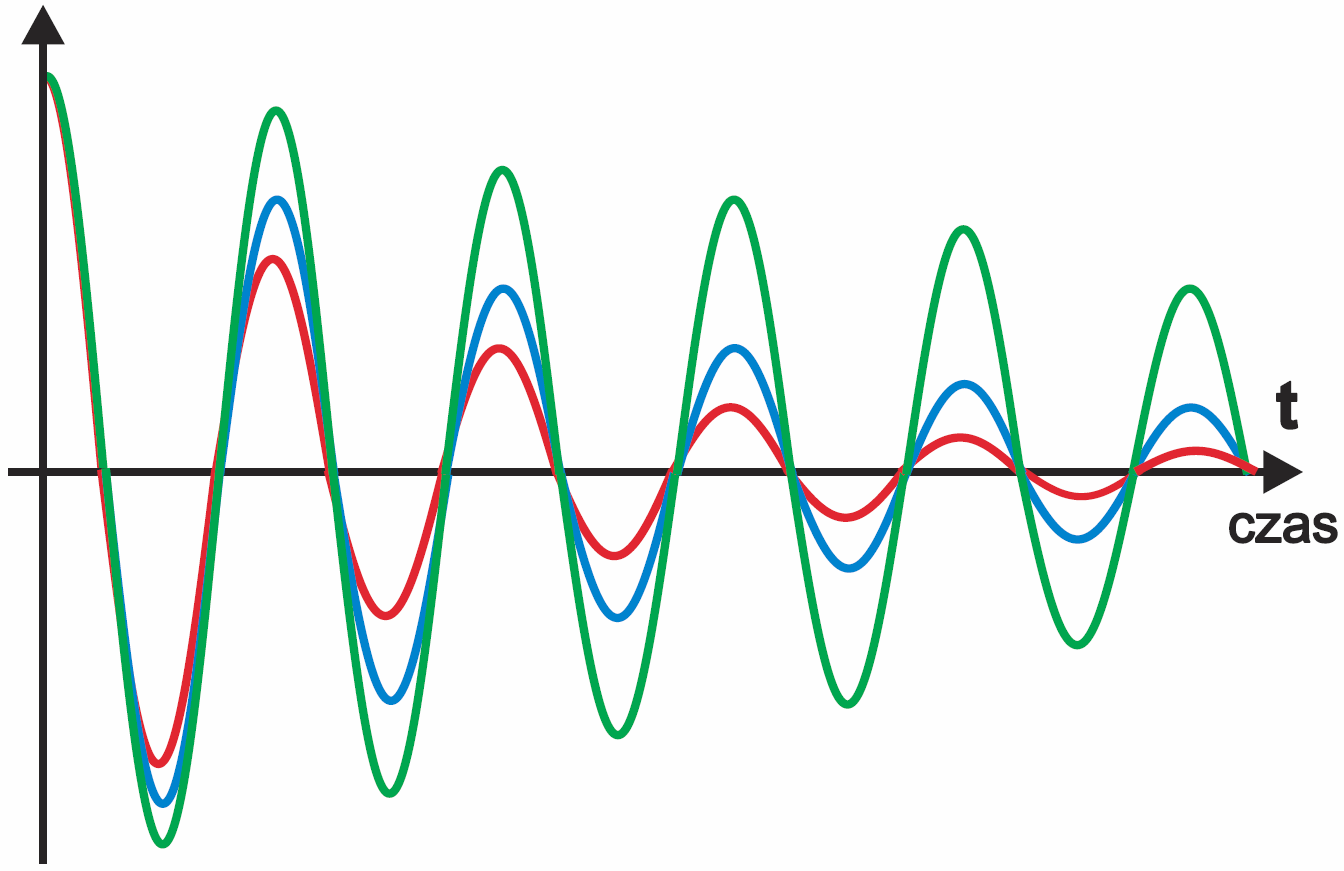
Już mówiliśmy, że w idealnym obwodzie LC raz wzbudzone drgania utrzymywałyby się wiecznie. W rzeczywistości, zależnie od wartości rezystancji R, drgania będą tłumione szybciej lub wolniej, jak pokazuje rysunek 7. Czym większa rezystancja szeregowa, tym szybciej zanikają drgania. Szybkość tłumienia drgań to kwestia bardzo ważna w praktyce.

Dla ścisłości należałoby dodać, iż zwiększanie wartości R powoduje też zmniejszanie częstotliwości drgań. Jednak zmiany te są niewielkie i w praktyce zazwyczaj możemy ten szczegół spokojnie pominąć.

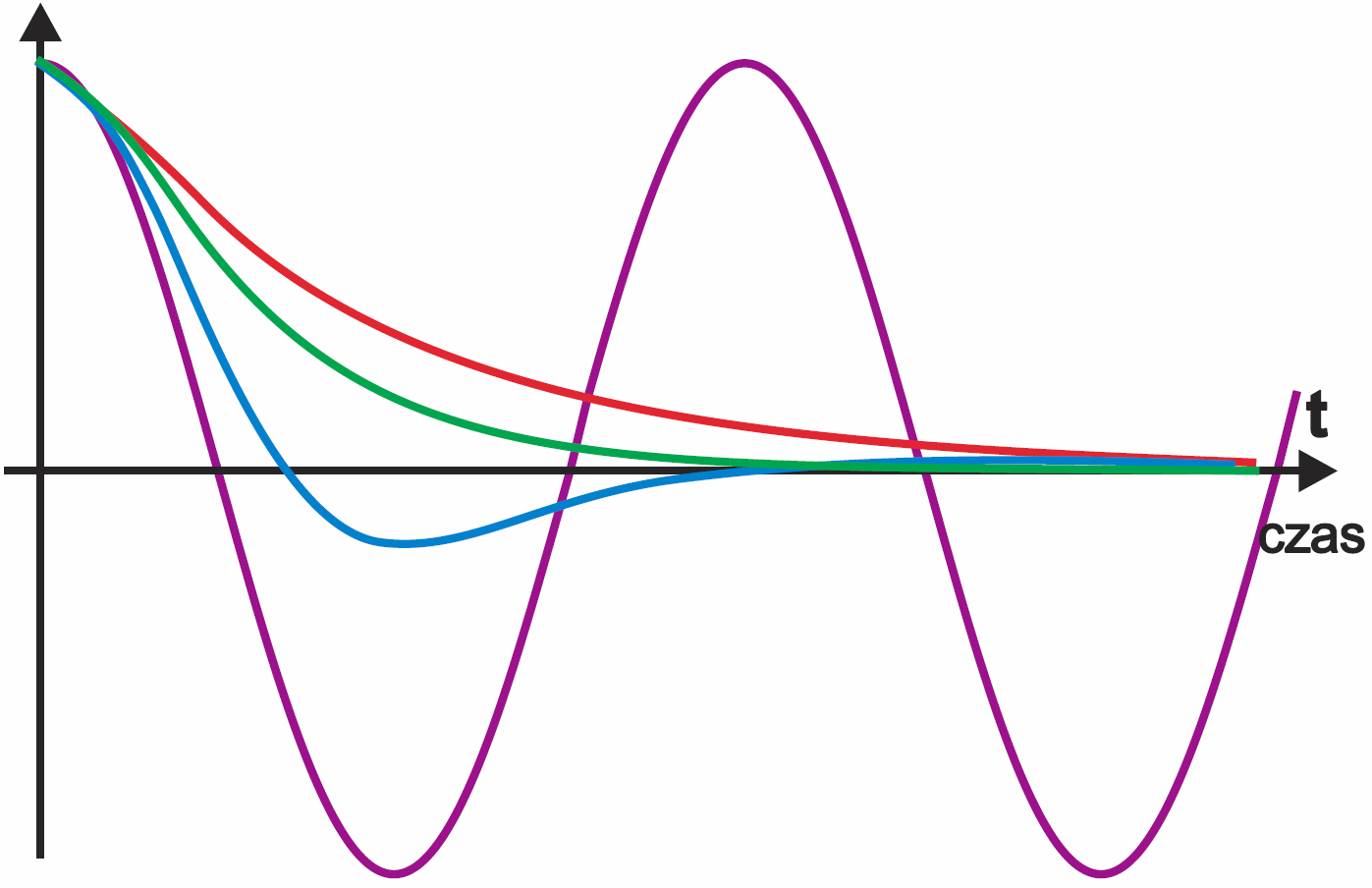
Należy też pamiętać, że obwód RLC zachowuje się w sposób pokazany na rysunku 7 wtedy, gdy rezystancja R jest znacznie mniejsza od oporności charakterystycznej ρ (ściślej biorąc, gdy R<2ρ). Już intuicja podpowiada, że gdy rezystancja strat dominuje, to drgania gasną tak szybko, że nawet nie można mówić o oscylacjach. Kilka przypadków szczególnych pokazanych jest na rysunku 8. Możemy sobie łatwo wyobrazić, iż przy dużej wartości R, drgania w ogóle nie powstaną i nastąpi płynne rozładowanie kondensatora przez rezystancję R i cewkę – taki przypadek ilustruje czerwona krzywa na rysunku 8.

Jednak w praktyce zazwyczaj interesują nas przypadki, gdy wartość oporności charakterystycznej ρ obwodu LC jest dużo większa od rezystancji R reprezentującej straty – wtedy drgania gasną stosunkowo powoli.

Wcześniej mówiliśmy o dobroci cewki jako stosunku X_L/R (Q=X_L/R) i stwierdziliśmy, że dana dobroć cewki zmienia się w funkcji częstotliwości, ponieważ X_L zależy od częstotliwości. Przypominam, że generalnie dobroć dotyczy strat energii (jest to stosunek energii magazynowanej w obwodzie LC i energii strat w jednym okresie drgań), ale my dla ułatwienia wolimy definiować ją za pomocą stosunku oporności. Teraz mówimy nie o pojedynczej cewce, tylko o obwodzie RLC i znów podobnie określamy dobroć jako stosunek reaktancji do rezystancji, ale tylko przy częstotliwości drgań swobodnych f₀ (przy pulsacji ω₀ drgań swobodnych):

Q = X_L/R = X_C/R = ρ/R

Q = ω₀L/R = 1/ω₀CR = ρ/R

Teraz już wiesz, do czego przydaje się oporność charakterystyczna ρ. Otóż pozwala łatwo obliczyć dobroć obwodu RLC:

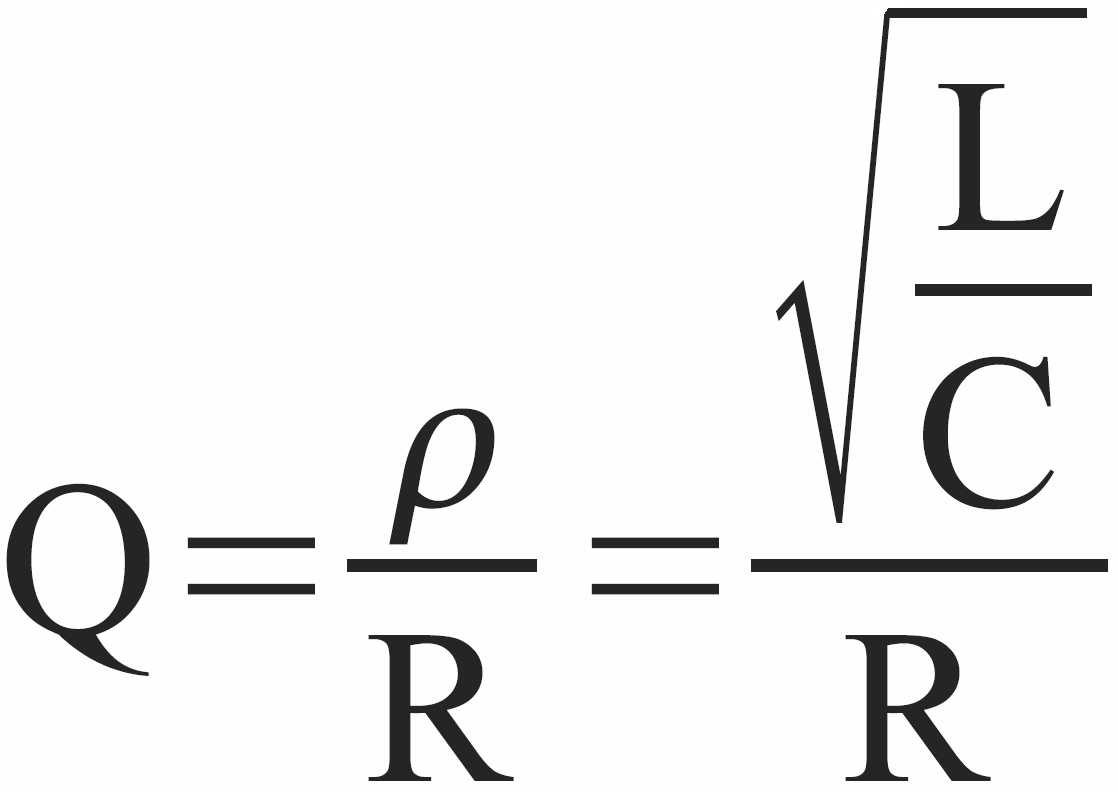
W praktycznych obwodach LC dobroć Q wynosi od kilkunastu do co najwyżej kilkuset.

Podkreślam, że w przypadku obwodu RLC interesują nas przede wszystkim właściwości przy jednej częstotliwości, przy częstotliwości drgań własnych f₀, i dlatego w ten sposób określona dobroć obwodu nie zmienia się – jest jedną konkretną liczbą. W następnym odcinku zajmiemy się obwodami rezonansowymi i przeanalizujemy, jakie praktyczne znaczenie ma tam dobroć.

Piotr Górecki