Elektronika (nie tylko) dla informatyków (22) Równoległy obwód rezonansowy

W poprzednim odcinku omówiliśmy szczegółowo szeregowy obwód rezonansowy. W tym odcinku przyjrzymy się bliżej równoległemu obwodowi rezonansowemu.

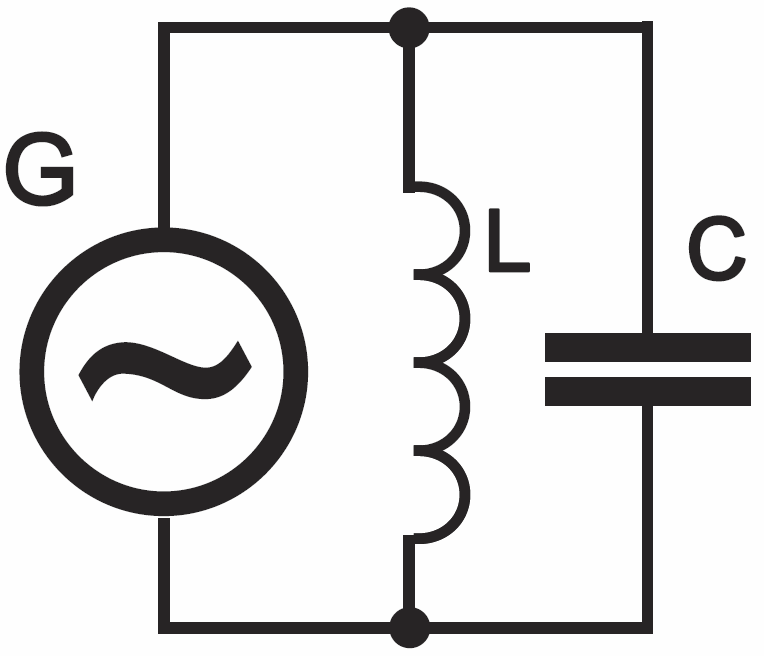
Już wcześniej mieliśmy do czynienia z równoległym obwodem LC , który traktowaliśmy jako źródło sinusoidalnych drgań swobodnych: w idealnym przypadku niegasnących, w rzeczywistości gasnących z uwagi na nieuchronne straty energii (patrz wcześniejsze rysunki 3–7 w tym odcinku). Mówiliśmy wtedy, że energia na przemian krąży tam między kondensatorem i cewką. Teraz będziemy mówić o rezonansie w takim obwodzie. I dlatego koniecznie muszę przypomnieć, że o rezonansie mówimy wtedy, gdy mamy do czynienia z drganiami wymuszonymi za pomocą zewnętrznego źródła. U nas dla uproszczenia rozważań niech to będzie źródło napięciowe przebiegu sinusoidalnego, jak pokazuje rysunek 1.

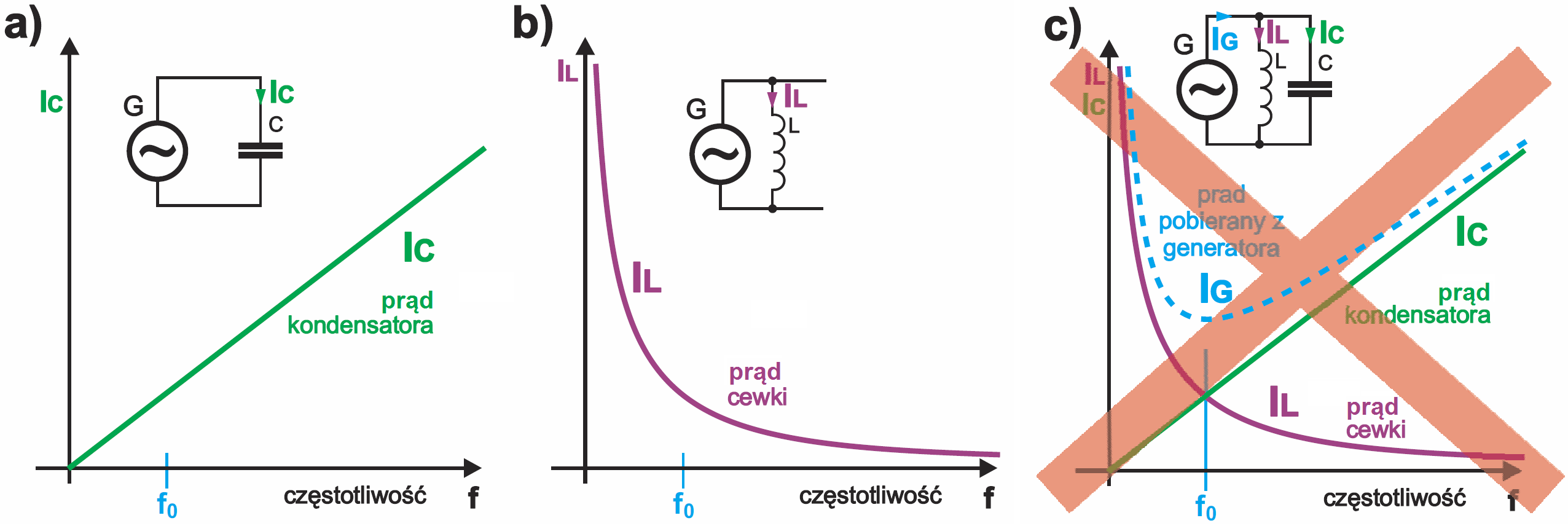
Idea jest prosta i jasna: napięcie U ze źródła przebiegu sinusoidalnego (generatora) powoduje przepływ prądu przez reaktancje X_L i X_C. Najpierw rozważmy więc sytuację dla dwóch oddzielnych obwodów zawierających źródło sygnału i jedną reaktancję. Jeśli częstotliwość przebiegu jest mała, to dla takich częstotliwości reaktancja X_C jest wielka i prąd I_C jest malutki. Natomiast przy tych małych częstotliwościach reaktancja X_L jest mała, a więc prąd I_L– duży. Ze wzrostem częstotliwości prąd I_C rośnie, a prąd I_L– maleje. Ilustrują to rysunki 2a oraz 2b.

Jeśli cewka i kondensator będą połączone równolegle, według rysunku 3c, to prądy będą się sumować i na pierwszy rzut oka można byłoby się spodziewać, że zmiany wypadkowego prądu w funkcji częstotliwości będą mniej więcej takie, jak pokazuje niebieska linia przerywana . Ale oczywiście tak nie jest, dlatego rysunek 3c jest przekreślony! Analogicznie jak w obwodzie szeregowym z rysunku 5 w tym wykładzie, jeśli uwzględnimy nie tylko wartość prądu, ale też przesunięcie fazowe, to wnioski i praktyczne obserwacje będą inne.

Jak pamiętasz z poprzedniego odcinka, przy częstotliwości rezonansowej oporność szeregowego obwodu rezonansowego była najmniejsza (w idealnym przypadku równa zeru), natomiast prąd – największy, jak pokazywały wcześniejsze rysunki 5, 6 i 9. Teraz mówimy o równoległym obwodzie rezonansowym. Co ciekawe, kształty krzywych prądu i oporności będą praktycznie takie same jak na rysunku 9 w poprzednim odcinku, jednak wykres w kształcie doliny nie będzie wykresem oporności, tylko przebiegiem prądu dostarczanego przez generator. Natomiast wykres w kształcie góry będzie przebiegiem oporności. Możemy więc mówić, że obwody rezonansowe: szeregowy i równoległy, są w pewnym sensie odwrotne. Teraz mówimy o rezonansie równoległym, o rezonansie prądów (bo następuje kompensacja prądów), który zwany jest przez niektórych antyrezonansem, co znów potwierdza, że zachowanie obwodów rezonansowych szeregowego i równoległego są w pewnym sensie odwrotne.

Ale wracajmy do równoległego obwodu rezonansowego z rysunku 1, który zasilany jest napięciem sinusoidalnie zmiennym U_G. Aby badać jego zachowanie przy różnych częstotliwościach, moglibyśmy wyprowadzić wzór na jego oporność (impedancję) i wtedy należałoby skorzystać ze znanego wzoru na równoległe połączenie dwóch elementów: 1/Z = 1/Z_L+ 1/Z_C lub jego wersji dla dwóch elementów: Z = (Z_L×Z_C)/(Z_L+Z_C). Jednak tak obliczony wynik w postaci:

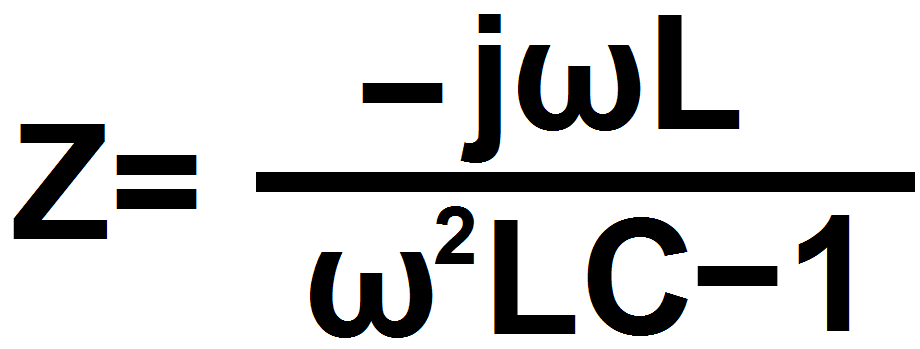
dałby niewiele pożytku, a analiza i przekształcenia nie są takie proste, dlatego zresztą w przypadku równoległego obwodu rezonansowego w podręcznikach często analizuje się odwrotność oporności, czyli przewodność (admitancję Y oraz jej składowe, konduktancję G i susceptancję S).

My podejdziemy do zagadnienia w sposób jeszcze bardziej uproszczony: otóż to oczywiste, że w układzie z rysunku 1 i 2c napięcie na połączonych równolegle elementach L, C jest zawsze jednakowe i równe napięciu generatora U_G. Przez elementy L, C płyną prądy o wartości wyznaczonej przez napięcie U_G i reaktancję danego elementu (I = U_G/X). A podczas rezonansu przebiegi prądu w cewce i kondensatorze mają identyczną wielkość, tylko przeciwne fazy. Podkreślam, że w stanie rezonansu przez elementy LC płyną prądy o kształcie sinusoidalnym i wartości:

I_C=I_L=U_G/X_C=U_G/ X_L = U_G/ρ

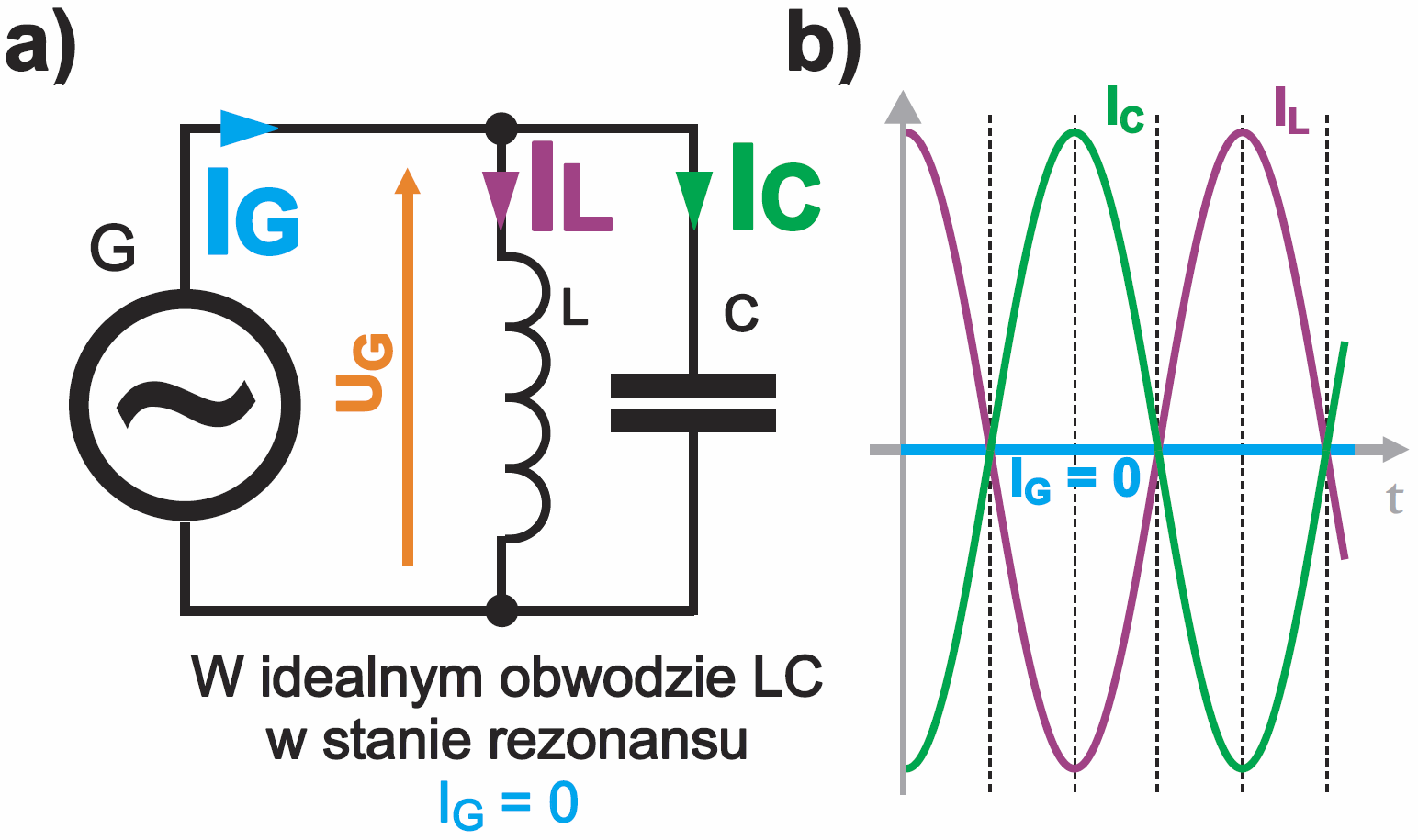
Rysunek 3 pokazuje przebiegi napięcia i prądu podczas rezonansu. Oznacza to, że prądy się znoszą i ze źródła sygnału (generatora) w ogóle nie jest pobierany prąd, czyli w rezonansie źródło nie dostarcza energii do obwodu LC.

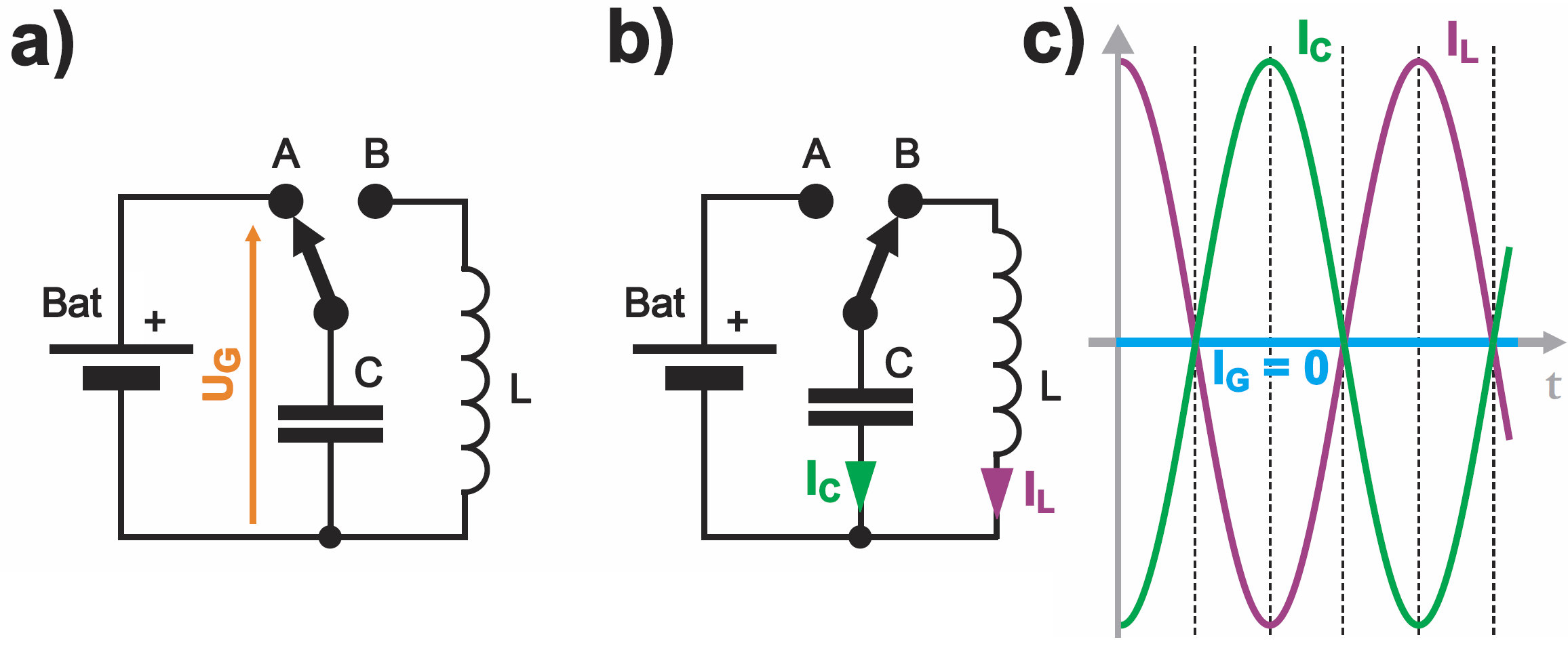
Jednak stwierdzenie, że prądy się znoszą, może być mylące. Dlatego warto to określić inaczej: gdy kondensator jest rozładowywany, to cewka jest ładowana i na odwrót, co należy rozumieć, że prądy mają przeciwne kierunki. I co ważne, w takim idealnym obwodzie w stanie rezonansu sytuacja wygląda dokładnie tak, jak w idealnym obwodzie LC bez generatora, wytwarzającym drgania swobodne, co pokazuje rysunek 4 – porównaj też wcześniejszy rysunek 3 w tym wykładzie.

Jak widać, w idealnym obwodzie z rysunku 3, podczas rezonansu źródło napięcia (generator) praktycznie nie wpływa na obwód LC. Moglibyśmy powiedzieć, że podczas rezonansu przebiegi w idealnym równoległym obwodzie LC są niezależne od generatora, tyle że są zsynchronizowane z jego przebiegiem.

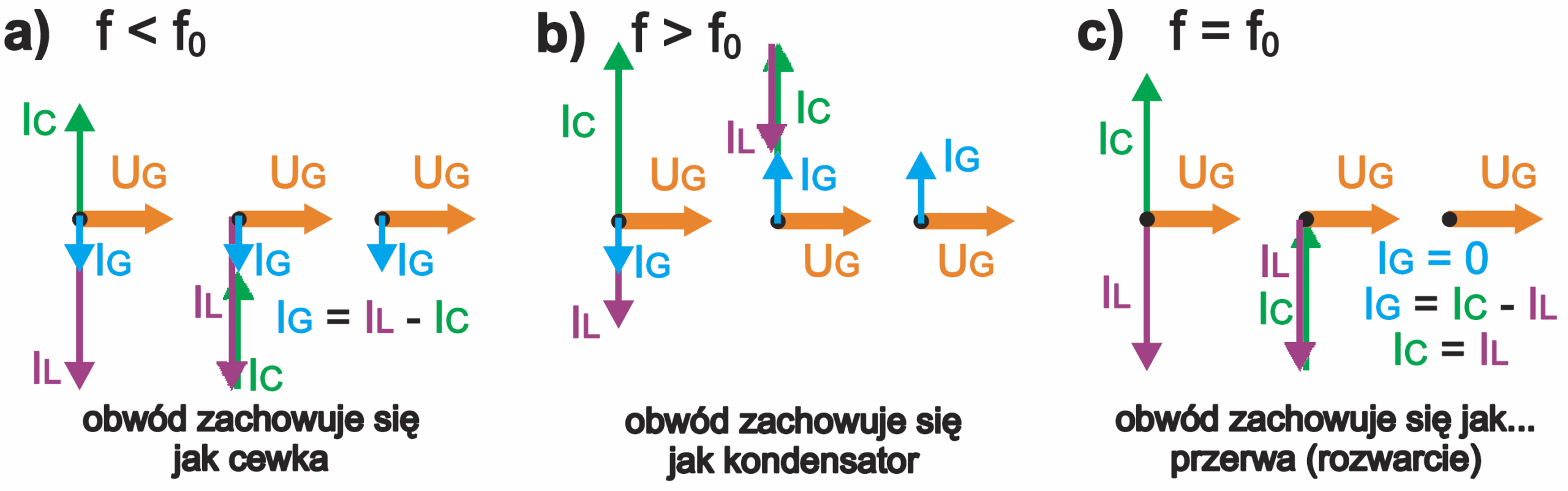
Warto też przeanalizować wykresy wskazowe. Otóż jak wskazuje rysunek 2, przy częstotliwościach mniejszych od rezonansowej prąd płynący przez cewkę jest większy od prądu kondensatora i różnica tych prądów to oczywiście prąd płynący przez generator – patrz przykład na rysunku 5a. Zauważ, że dla takich częstotliwości, mniejszych od f₀, obwód LC zachowuje się jak cewka. Natomiast dla częstotliwości większych od f₀ prąd kondensatora jest większy od prądu cewki i obwód zachowuje się jak kondensator – rysunek 5b.

Źródło zasilające – generator, zależnie od częstotliwości, „widzi” taki obwód rezonansowy albo jako cewkę, albo jako kondensator.

I tu jeszcze jeden szczegół: w obwodzie nie ma rezystancji. Nie ma więc strat w postaci ciepła. W obwodzie generator–obwód LC płynie prąd, ale przepływająca energia elektryczna nie zamienia się na ciepło. Jest to prąd sinusoidalnie zmienny i okazuje się, że przez część okresu transportuje on energię do obwodu LC, który „widzi” albo jako cewkę, albo jako kondensator. Przez drugą część okresu prąd ten przenosi energię z powrotem z obwodu LC do generatora.

Jeszcze raz podkreślam, że w idealnym obwodzie LC nie ma strat energii w postaci ciepła. Płynące prądy na przemian przenoszą energię pomiędzy generatorem, cewką i kondensatorem.

Przy częstotliwości rezonansowej wektory prądu cewki i kondensatora mają dokładnie jednakową długość i przeciwne zwroty więc znoszą się – wypadkowy prąd płynący ze źródła-generatora staje się równy zeru – rysunek 5c. Przy tej częstotliwości generator „widzi” równoległy obwód LC jako przerwę, rozwarcie, czyli nieskończenie wielką oporność – rezystancję. Ale w obwodzie w stanie rezonansu nadal płynie prąd – energia przenoszona jest cyklicznie między cewką a kondensatorem.

Zwróć uwagę, że jeśli dla dużych częstotliwości obwód LC zachowuje się jak kondensator, to przesunięcie wynosi dokładnie +90 stopni (+π/2). W idealnym obwodzie dla wszystkich częstotliwości większych od f₀ przesunięcie fazy jest jednakowe i wynosi dokładnie +90 stopni. Czym bliżej częstotliwości f₀, tym mniejszy jest prąd, a tym większa wypadkowa reaktancja pojemnościowa Xc, która jest jednocześnie impedancją (opornością wypadkową) obwodu. Natomiast dla częstotliwości mniejszych od f₀ obwód zachowuje się jak cewka i przesunięcie fazy między napięciem i prądem niezmiennie wynosi –90 stopni (–π/2). Czym bliżej częstotliwości rezonansowej, tym mniejszy prąd i tym większą wartość ma impedancja (wypadkowa oporność), która jest reaktancją indukcyjną. Przy okazji można wspomnieć, że określenie, czy kąt jest dodatni, czy ujemny, to kwestia umowy: czy określamy go jako przesunięcie między prądem i napięciem, czy między napięciem i prądem? To jest mało istotne, w każdym razie przesunięcie to jest albo równe 90°, albo –90°.

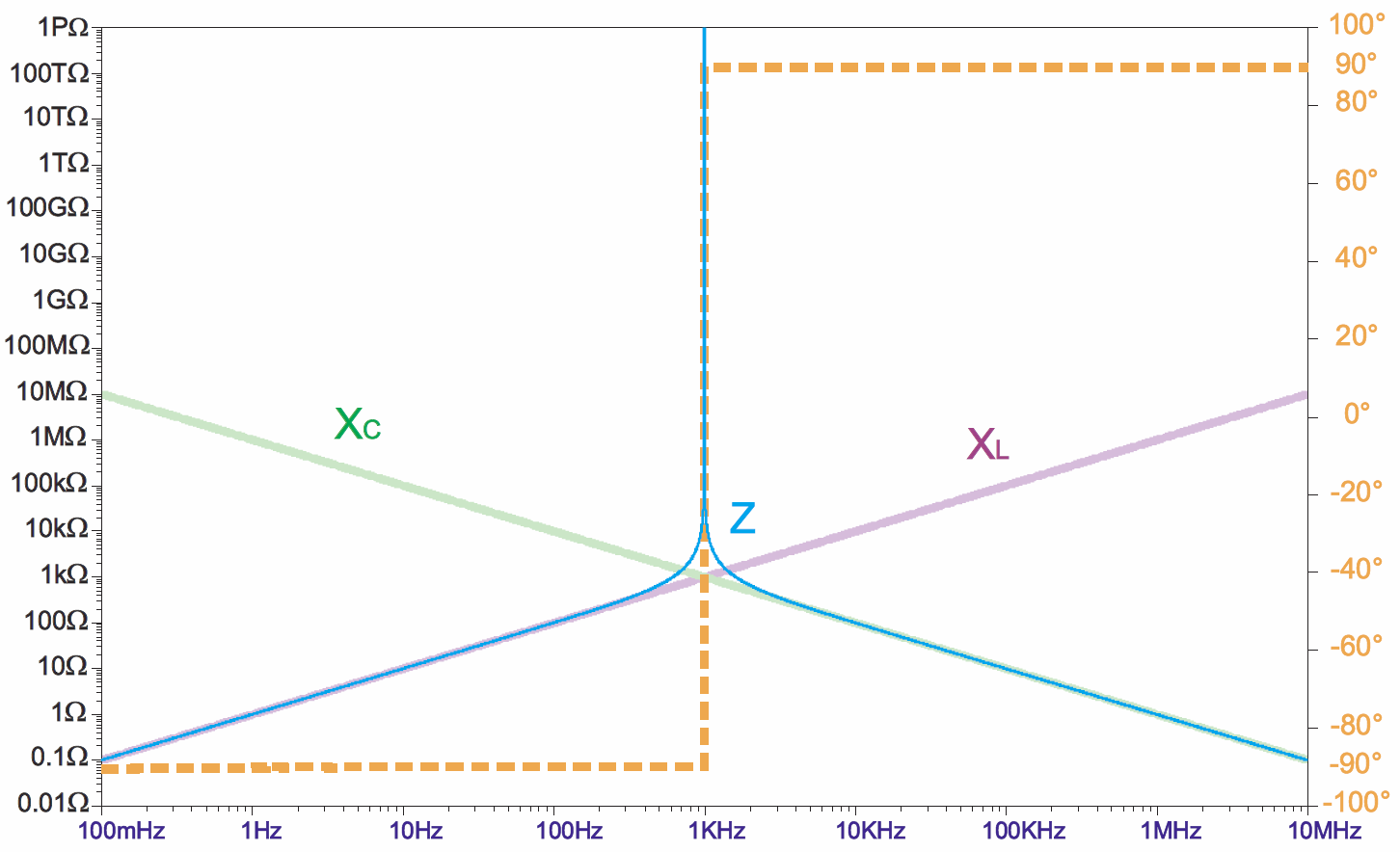
Natomiast dla jednej jedynej częstotliwości f₀ prąd jest równy zeru, czyli impedancja wypadkowa jest nieskończenie wielka. W zasadzie jeśli nie ma prądu, to nie możemy mówić o przesunięciu między napięciem i prądem, ale uznajemy, że obwód jest wtedy rezystancją o nieskończenie wielkiej wartości i przesunięcie jest równe zeru. Ilustruje to rysunek 6, pokazujący oporności i przesunięcie fazy w idealnym obwodzie LC o częstotliwości rezonansowej 1 kHz.

Pomarańczowa linia przerywana i skala z prawej strony pokazują przesunięcie fazy między napięciem U_G i prądem I_G – porównaj rysunek 5. Zielona linia to reaktancja kondensatora, która oczywiście maleje ze wzrostem częstotliwości. Fioletowa linia to reaktancja cewki, która rośnie z częstotliwością. W zasadzie są to odpowiedniki rysunków 2a i 2b, tylko teraz mamy zobrazowany nie przebieg prądu, lecz oporności, a dodatkowo wykorzystaliśmy skalę podwójnie logarytmiczną, dzięki czemu wykresy są ładnymi liniami prostymi. Cienka niebieska linia na rysunku 6 to impedancja – oporność wypadkowa obwodu LC. Zwróć uwagę, że tylko w okolicach częstotliwości rezonansowej, w zakresie częstotliwości mniej więcej 0,2f₀ do około 5f₀, impedancja jest zauważalnie inna od jednej z reaktancji X_L, X_C.

Jak widzisz, w rezonansie równoległym też nie ma nic tajemniczego i nadzwyczajnego – wszystko zgadza się z fundamentalnymi prawami fizyki. Ale pamiętaj, że jak na razie mówiliśmy o nierealnej, teoretycznej sytuacji, ponieważ w praktyce w każdym obwodzie LC występują straty i bardzo interesuje nas zachowanie takich niedoskonałych obwodów przy częstotliwościach zbliżonych do częstotliwości rezonansowej.

Równoległy obwód RLC

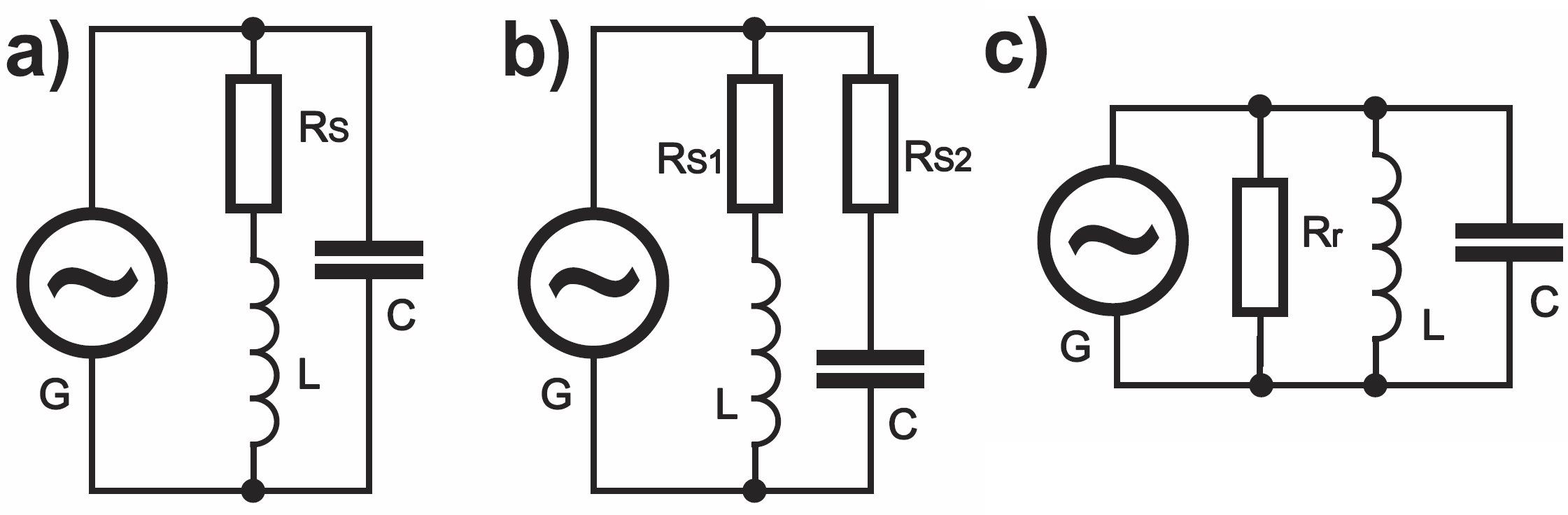
Możemy zobrazować straty tak, jak robiliśmy do tej pory, czyli w postaci rezystancji szeregowej R_s, jak na rysunku 7a. Moglibyśmy, tak jak to bywa w podręcznikowych analizach, uwzględniać straty w obu elementach reaktancyjnych według rysunku 7b. Jednak, jak już ustaliliśmy wcześniej (rysunki 1, 2 w tym wykładzie), dla rezonansu równie dobrze straty może reprezentować rezystancja R_r włączona równolegle, jak pokazuje rysunek 7c. Oczywiście taka równoległa rezystancja strat R_r będzie duża, tym większa, im mniejsze straty będą występować w obwodzie, czyli im większa będzie jego dobroć, że przypomnę zależność Q = ρ/Rs = Rr/ρ

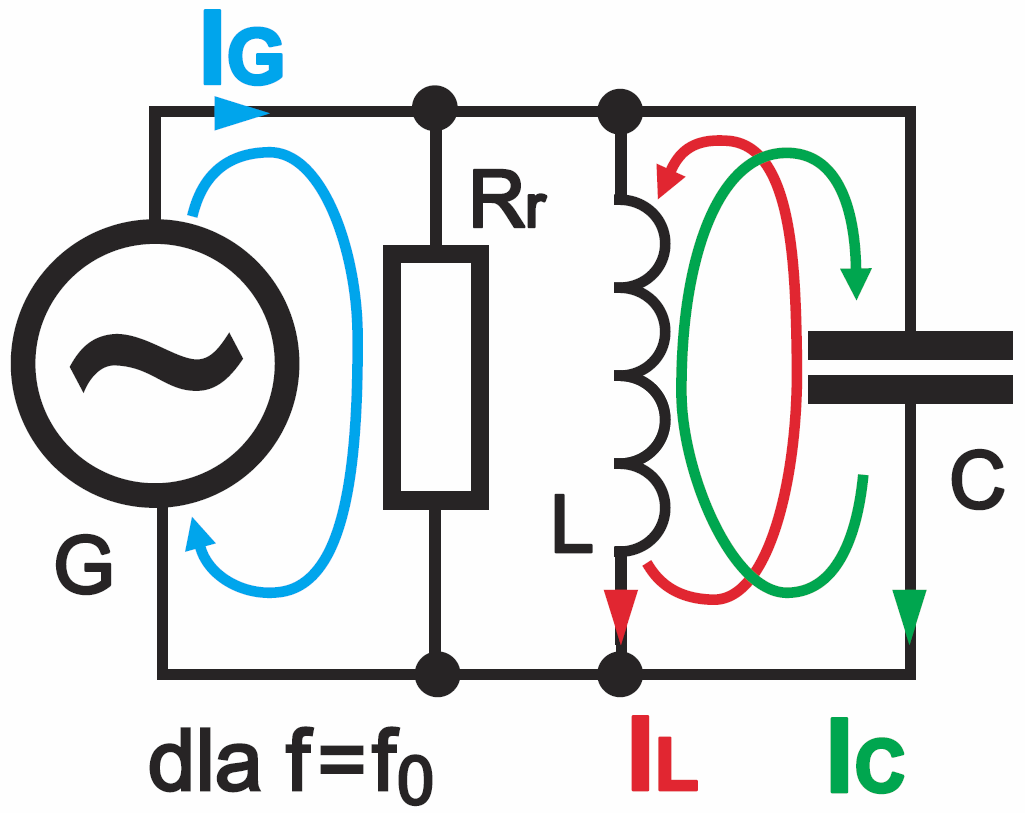
Ściśle biorąc, obwody RLC o schematach z rysunku 7 wcale nie mają identycznych właściwości. Trzeba jednak pamiętać, że cały czas chodzi tu jedynie o uproszczone schematy zastępcze i żaden z nich nie odwzorowuje w pełni zachowania rzeczywistego obwodu rezonansowego. Godzimy się na takie uproszczenia, bo chcemy omówić tylko podstawowe, najważniejsze zależności. Choć więc schemat z rysunku 7a nieco lepiej odpowiada rzeczywistości niż pozostałe, dla ułatwienia analizy wykorzystajmy schemat z rysunku 7c. Gdybyśmy bowiem próbowali wykorzystać schemat zastępczy z rysunku 7a z rezystancją szeregową R_s, natknęlibyśmy się na skomplikowane wzory. Natomiast przyjęcie schematu zastępczego z rysunku 7c genialnie uprości rozważania. Zobacz zresztą sam: wcześniej ustaliliśmy, że w idealnym równoległym obwodzie LC podczas rezonansu prąd generatora I_G jest równy zeru – rysunek 3. Biorąc pod uwagę te wcześniejsze wnioski i rysunek 4, możemy powiedzieć, że teraz w nieidealnym obwodzie RLC z rysunku 7c przy częstotliwości rezonansowej nadal generator nie będzie wpływał na prądy I_C, I_L, krążące między cewką i kondensatorem, natomiast z generatora popłynie prąd tylko przez równoległą rezystancję strat R_r. Ilustruje to rysunek 8.

A jeśli tak, to mamy ważny i jakże prosty wniosek: o ile w obwodzie idealnym oporność podczas rezonansu była nieskończenie wielka, to teraz oporność niedoskonałego obwodu będzie równa R_r! Co możemy zapisać: R_r = Q×ρ

Można to rozumieć w prosty sposób sugerowany przez rysunek 8: w obwodzie występuje równoległa rezystancja strat R_r i podczas rezonansu prąd pobierany ze źródła sygnału płynie wyłącznie przez tę rezystancję. Ale sens rezystancji strat warto i należy rozumieć mniej więcej tak: jeśli obwód LC jest niedoskonały i występują w nim straty, to w przypadku rezonansu straty te powinny być uzupełniane ze źródła przebiegu wymuszającego. Ze źródła tego popłynie więc prąd taki, żeby przenoszona energia skompensowała straty, by utrzymać potrzebną amplitudę drgań. W każdym razie, w stanie rezonansu oporność wypadkowa rzeczywistego obwodu LC jest duża i jest równa zastępczej (równoległej) rezystancji strat R_r.

W podręcznikach spotkasz też informację, że w stanie rezonansu prąd w elementach LC jest Q razy większy od prądu pobieranego ze źródła. Tak, to prawda i wynika to bezpośrednio z analizowanych wzorów. Bo przecież z rysunków 3, 4, 7 wynika że: I_L = I_C = U_G/ρ natomiast I_G = U_G/R_r = U_G/Q stąd I_L = I_C = Q×I_G

Rzeczywiście, prąd w cewce i kondensatorze może być setki razy większy od prądu „wymuszającego”, pobieranego ze źródła (I_G). W idealnym obwodzie LC byłby nieskończenie razy większy od prądu pobieranego ze źródła. I tu niektórzy początkujący gotowi byliby dojść do wniosku, że podczas rezonansu, prąd w elementach L, C może wzrastać nieskończenie lub choćby do bardzo wielkiej wartości, co znów przypomina most w Angers (fotografia 3 w poprzednim odcinku) i rodzi groźbę jakiejś katastrofy.

Bez przesady! Owszem prądy I_L, I_C będą wielokrotnie większe od prądu „pobudzającego” I_G, ale tylko dlatego, że ten prąd pobudzający będzie mały i przy wzroście Q będzie dążył do zera.

Zauważ, że przy danym napięciu z generatora, prąd nie może nieograniczenie rosnąć. Prąd płynący przez L, C praktycznie nie zależy od dobroci obwodu. Przecież nadal obowiązuje prawo Ohma i podstawowa zależność I = U/R (ogólnie I = U/Z, w tym przypadku dla obu reaktancji: I = U/X). Przy zasilaniu jakimś określonym napięciem U_G, podczas rezonansu prąd w cewce i kondensatorze będzie więc miał jakąś niezbyt dużą wartość, wyznaczoną przez napięcie zasilające (napięcie oscylacji) i oporność charakterystyczną : I_fo= UG/ρ .

Wraz ze zwiększaniem dobroci, czyli zwiększaniu rezystancji zastępczej R_r, malał będzie tylko prąd I_G, pobierany ze źródła zasilania. Będzie się zwiększał tylko stosunek tych prądów, a nie prądy I_L, I_C, więc nie ma tu widoków na katastrofę.

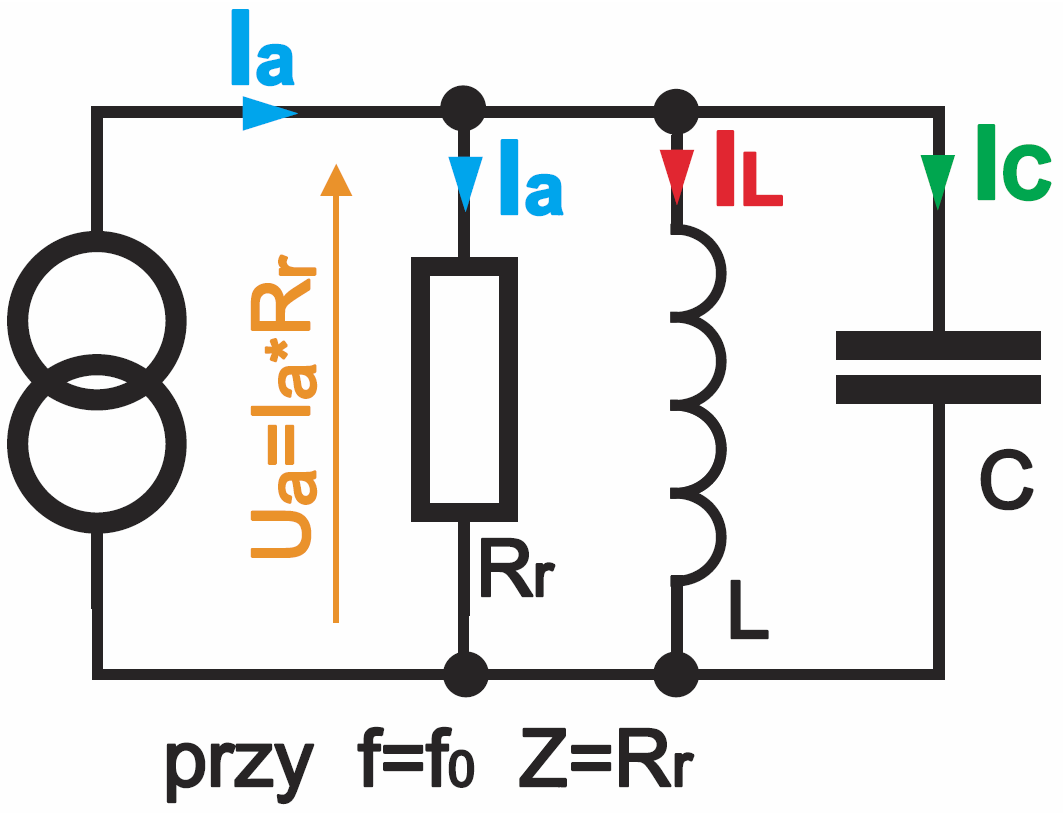
W rozpatrywanym układzie prądy I_L, I_C są ograniczone przez napięcie generatora U_G. Owszem, prądy te mogłyby rosnąć, gdyby generator nie był źródłem napięciowym, tylko prądowym, według rysunku 9. Jak wiemy, napięcie źródła prądowego nie jest określone – wynika ono z oporności obciążenia według zależności U = I×R (ściślej U = I×Z). Czym większa oporność obciążenia, tym większe napięcie.

Dołączając równoległy obwód LC o dużej dobroci i dużej rezystancji R_r do dającego przebieg sinusoidalny źródła prądowego, moglibyśmy uzyskać przy częstotliwości rezonansowej bardzo duże napięcie i tym samym prąd w cewce i kondensatorze. Słusznie spodziewamy się, że i tu prąd cewki i kondensatora w rezonansie będzie Q razy większy od prądu zasilania. I rzeczywiście: wypadkowa oporność obwodu w rezonansie będzie równa R_r, a więc prąd źródła I_a wywoła na tej oporności, a tym samym także na elementach L, C, napięcie równe U_a = I_a×R_r

To napięcie będzie też występować na reaktancjach X_L, X_C, a to oznacza, że będzie tam płynąć prąd I_L, I_C o wartości

I_L = I_C = U_a/X_L = U_a/X_C = U_a/ρ = Ia×Rr/ρ a ponieważ R_r = Q×ρ , więc I_L = I_C = I_a×Q×ρ/ρ = I_a×Q

I w tym wypadku widać ryzyko katastrofy! Ale jak wiemy, w rzeczywistości nie ma dobrych źródeł prądowych, gdzie napięcie mogłoby nieograniczenie rosnąć. Niemniej faktem jest, że w układach elektronicznych dość często równoległy obwód rezonansowy włączony jest w obwód kolektora tranzystora, który ma cechy źródła prądowego. Wtedy istotnie na obwodzie rezonansowym mogą wystąpić napięcia, wyższe od napięcia zasilania. Do tego szczegółu jeszcze wrócimy. A w następnym odcinku będziemy badać jeszcze inne cechy równoległego obwodu rezonansowego.

Piotr Górecki