Podstawy układów cyfrowych – układy kombinacyjne

Elektronika cyfrowa to ogromny dział ogólnie pojętej elektroniki i by w nią się zagłębić, należy zacząć od układów kombinacyjnych. By zbudować dom, konieczne jest stworzenie solidnych fundamentów. Układy kombinacyjne są właśnie tymi fundamentami.

Co to jest układ kombinacyjny

W poprzedniej części (D050) mowa była o podstawowych bramkach występujących w układach cyfrowych. Na bazie tych elementów możliwe staje się zbudowanie różnych funkcji logicznych, które przetwarzają sygnały wejściowe generując określone sygnały wyjściowe. To przetwarzanie ma jedną bardzo istotną cechę: stan sygnałów na wyjściu zależy jedynie od stanu występującego na wejściu układu.

W pierwszej chwili nasuwa się wniosek, że to zdanie jest dziwne. Przecież zawsze jest tak, że na wyjściu jest coś zdeterminowane określonym wymuszeniem (na wejściu). Jeżeli za każdym razem na wejście wzmacniacza (choćby akustycznego) podamy sygnał o częstotliwości 1 kHz, to na wyjściu uzyskamy ten sam sygnał. W układach cyfrowych to już tak nie jest, gdyż te mogą zawierać w swojej strukturze elementy „pamięci”, której stan może mieć wpływ na sygnał wyjściowy i jednocześnie wpływ na stan tej „pamięci”. Oprócz poznanych dotychczas bramek, elektronika cyfrowa dysponuje drugą klasą elementów, jakimi są przerzutniki. Te elementy mają możliwość zapamiętania stanów logicznych, toteż w rozwiązaniach zawierających przerzutniki, stan na wyjściu układu zależny jest od sygnałów wejściowych oraz od stanów wcześniejszych, zapamiętanych w przerzutnikach.

Ta klasa układów logicznych jest określana jako układy sekwencyjne i mowa o nich będzie w kolejnych częściach. Ich przeciwieństwem są układy kombinacyjne, w których nie występują elementy „pamięci”. Ich wyjścia są uzależnione jedynie od wejścia i można tu doszukiwać się analogii do wspomnianego właśnie wzmacniacza.

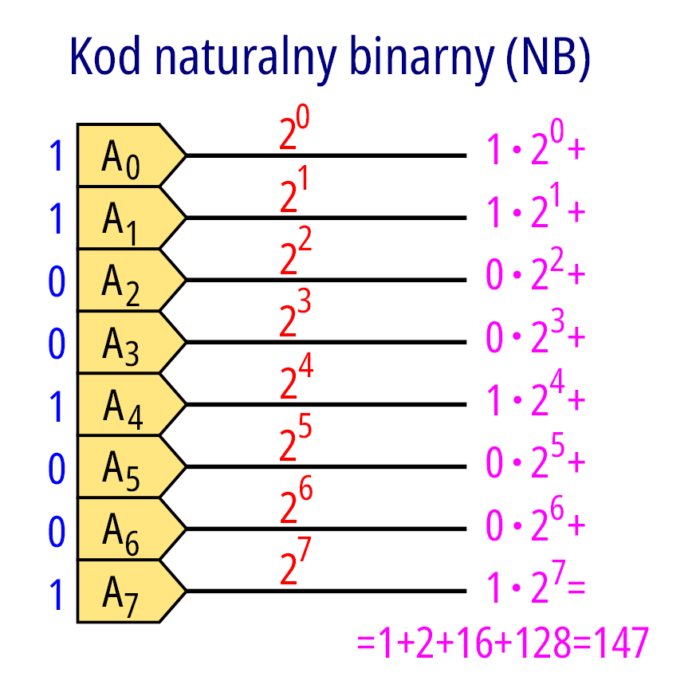
Kod naturalny binarny

Informacje bitowe, jako ciągi bitowe, przetwarzane w układach kombinacyjnych (jak i sekwencyjnych) można interpretować jako liczby, przykładowo jako liczbę bez znaku. W technice mikroprocesorowej/komputerowej mówi się o kodach binarnych. Jednym z nich jest kod binarny naturalny (często oznaczany jako NB), gdzie dla każdego bitu przyporządkowana jest jego dwójkowa waga. Przykład 8-bitowego kodu i sposób przeliczenia na postać powszechnie używaną przez ludzi pokazuje rysunek 1.

Kod 1 z n

Oprócz kodu naturalnego binarnego, w układach cyfrowych często pojawia się kod 1 z n. Cechą charakterystyczną tego kodu jest wystąpienie stanu wyróżnionego jedynie na jednej pozycji. Tym stanem może być jedynka logiczna znajdująca się na jednej pozycji (pozostałe sygnały mają wartość zera logicznego). W takim przypadku mowa jest o prostym kodzie 1 z n. Innym wariantem jest wystąpienie logicznego zera dla jednego sygnału, gdzie wszystkie pozostałe są jedynkami. W takim przypadku mowa jest o zanegowanym kodzie 1 z n.

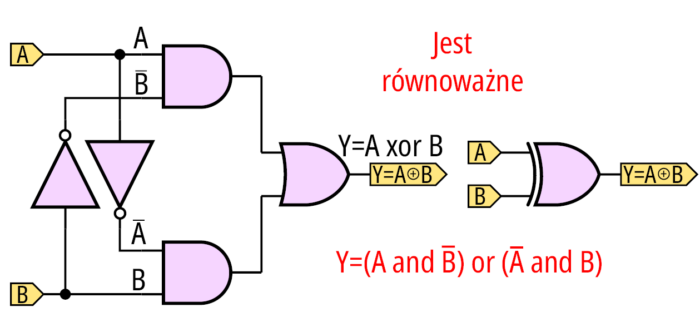
Bramka XOR

Obok poznanych bramek iloczynu i sumy logicznej w praktyce występuje jeszcze bramka XOR (od ang. Exclusive OR), której realizację, symbol i równanie logiczne pokazuje rysunek 2. Nie wymieniłem jej w części poświęconej bramkom, gdyż nie należy ona do podstawowych elementów logicznych (AND, OR, NOT), ale może zostać zbudowana na bazie tych elementów. Bramka XOR realizuje funkcję, która ma wiele określeń jak: alternatywa rozłączna, alternatywa wyłączająca, różnica symetryczna, suma modulo 2.

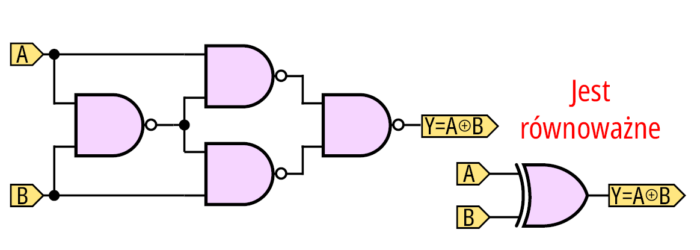
Alternatywa rozłączna dwóch argumentów jest prawdziwa wtedy, gdy jeden i tylko jeden z argumentów jest prawdziwy, co przekłada się na stany logiczne w następujący sposób: funkcja przyjmuje stan jedynki logicznej jeżeli tylko jeden stan na wejściu odpowiada logicznej jedynce. Popularną realizacją bramki XOR jest wariant oparty na bramkach NAND (rysunek 3, rozwiązanie z rysunku 2 wymaga użycia trzech układów z rodziny 7400, natomiast z rysunku 3 zamyka się w obrębie jednego układu scalonego). Oczywiście są produkowane gotowe bramki XOR, w rodzinie układów TTL mają oznaczenie SN74xx86, w rodzinie CMOS oznaczenie CD4070.

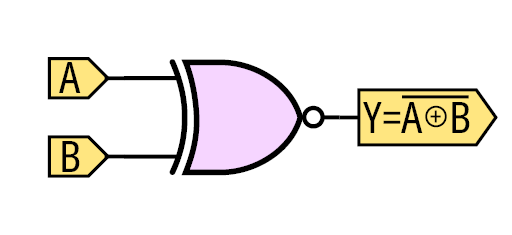
Podobnie, jak w podstawowych bramkach są bramki z negacją na wyjściu, tu również występują bramki XOR z wbudowaną negacją skrótowo określane jako bramki XNOR (symbol bramki pokazuje rysunek 4, bramka XOR z „kółkiem” na wyjściu).

Komparatory

Bramka XOR ma ciekawą funkcjonalność. Patrząc na jej realizowaną funkcję (równanie jest pokazane na rysunku 2), którą można określić jako: na wyjściu jest jedynka logiczna jeżeli argumenty mają różną wartość logiczną (zero logiczne dla argumentów mających identyczną wartość), to rodzi się natychmiastowe skojarzenie z funkcją komparatora: układu porównującego ciągi bitów. Bazując na bramce XOR realizuje się jednobitowy komparator stanów (dający zero logiczne na wyjściu dla identycznych stanów na obu wejściach).

(…) ciach!

To jest tylko początek, zapowiedź artykułu, którego pełna wersja ukazała się z numerze czerwcowym czasopisma Zrozumieć Elektronikę (ZE 7/2023). Pełna wersja czasopisma umieszczona jest pod tym linkiem. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 7/2023 znajduje się tutaj.

 

Andrzej Pawluczuk

apawluczuk@vp.pl

Uwaga! Osoby, które nie są (jeszcze) stałymi Patronami ZE, mogą nabyć PDF-y z pełną wersję tego numeru oraz wszystkich innych numerów czasopisma wydanych od stycznia 2023, „stawiając kawę” (Cappuccino = 10 złotych za jeden numer czasopisma w postaci pliku PDF).
W tym celu należy kliknąć link (https://buycoffee.to/piotr-gorecki), lub poniższy obrazek

Następnie wybrać:
– jeśli jeden numer ZE – CAPPUCINO (10zł),
– jeśli kilka numerów ZE – WSPIERAM ZA. I tu wpisać kwotę zależną od liczby zamawianych numerów – wydań (N x 10zł),
Wpisać imię nazwisko.
Podać adres e-mail.
Koniecznie zaznaczyć: „Chcę dołączyć wiadomość dla Twórcy” i tu wpisać, który numer lub numery mamy wysłać na podany adres e-mailowy.