Pierwsze kroki w cyfrówce – część 3

W poprzedniej części zapoznałem Cię z podstawowymi bramkami logicznymi: AND, OR, NAND, NOR oraz NOT. W tym odcinku omówimy bramki złożone: EX−OR i EX−NOR oraz sprawę logiki ujemnej.

Inne bramki

Istnieją też elementy logiczne, realizujące jeszcze inne funkcje. Zapewne spotkałeś już określenie EX−OR i EX−NOR. Elementy takie również nazywamy bramkami. W literaturze niekiedy są oznaczane jako bramki XOR lub XNOR. Elementów tych z pewnością będziesz używał w swoich układach.

Na pewno chciałbyś intuicyjnie zrozumieć ich działanie, a jest ono bardzo proste.

Spróbuj zapamiętać: na wyjściu dwuwejściowej bramki EX−OR pojawia się stan wysoki, gdy na wejściach występują różne stany logiczne. Natomiast gdy oba wejścia mają ten sam stan logiczny (obojętnie czy wysoki, czy niski), na wyjściu występuje stan niski.

Bramka EX−NOR działa tylko trochę inaczej − gdy stan wejść jest jednakowy, na wyjściu pojawia się stan wysoki, gdy stany są różne − stan niski.

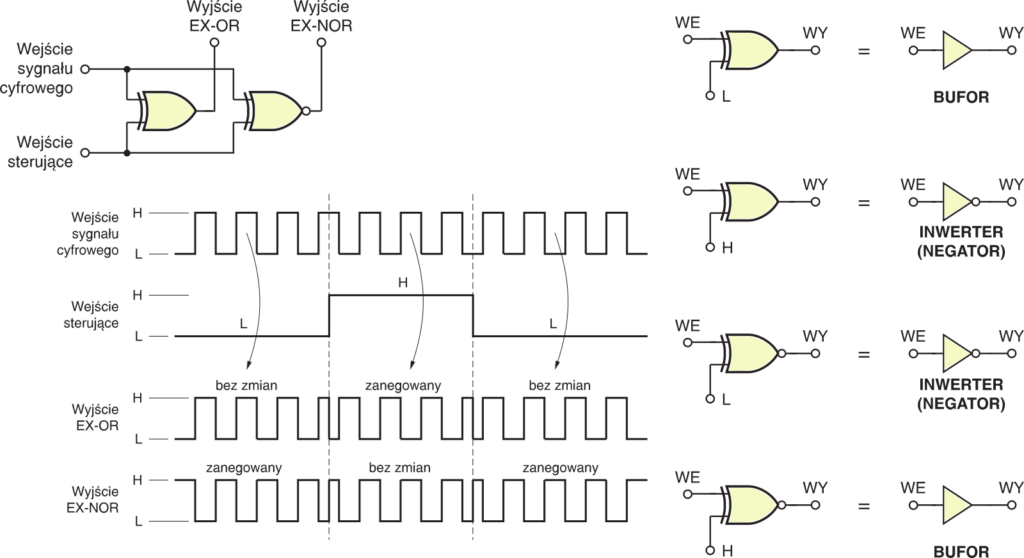
Jest to rzeczywiście proste. Na rysunku 1 znajdziesz symbole i opis działania bramek: EX−OR i EX−NOR.

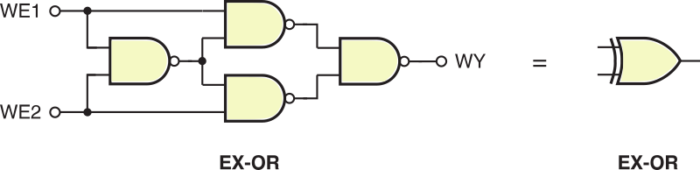
Na rysunku 2 zobaczysz, jak wykonać bramkę EX−OR z bramek NAND. W praktyce nigdy się tak nie robi, bowiem produkowane są układy scalone zawierające po cztery bramki EX−OR albo EX−NOR w jednym układzie scalonym.

Do czego wykorzystasz w praktyce bramki EX−OR i EX−NOR?

Najczęściej do sprawdzenia, czy dane sygnały mają takie same poziomy logiczne. Ale nie tylko.

Na rysunku 3 zobaczysz inną możliwość, przydatną w praktyce: w zależności od stanu na jednym z wejść, bramka EX−OR (lub EX−NOR) neguje sygnał wejściowy, albo przepuszcza go bez zmian.

Zapamiętaj właściwość pokazaną na rysunku 3 − przyda ci się, gdy w trakcie projektowania zagospodarujesz bramki EX−OR i EX−NOR nie wykorzystane w swej klasycznej roli.

Może zapytasz jeszcze, czy istnieją wielowejściowe bramki EX−OR i EX− NOR? W praktyce spotkasz się tylko z bramkami dwuwejściwymi. Bramki te można w prosty sposób łączyć, by uzyskać coś podobnego do bramki wielowejściowej, ale stosuje się to bardzo rzadko. Istnieją też wielowejściowe układy zwane generatorami i kontrolerami parzystości, przeznaczone do systemów przesyłania danych − ich działanie nieco przypomina działanie opisywanych bramek.

Uważaj teraz! W starej krajowej literaturze lub w publikacjach obcojęzycznych spotyka się odmienne symbole bramek (oraz innych układów logicznych). Żeby nie robić ci wody z mózgu, na poprzednich rysunkach podałem ci najczęściej spotykane oznaczenia, występujące w większości dostępnych dziś źródeł.

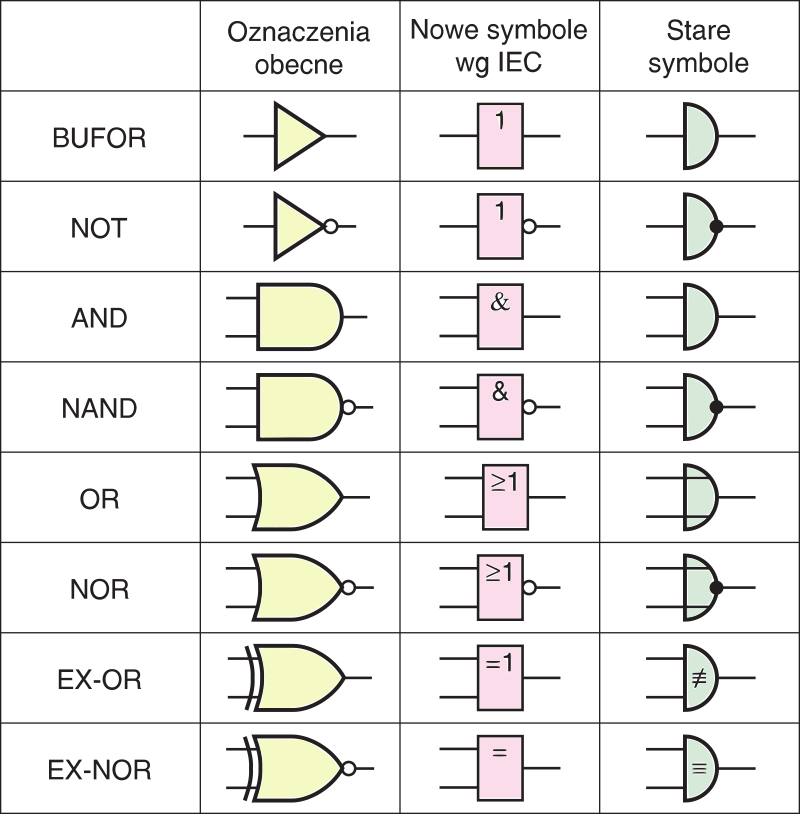
Na rysunku 4, w pierwszej kolumnie znajdziesz oznaczenia według dotychczas obowiązujących norm krajowych, w drugiej kolumnie nowe oznaczenia, zgodne z zaleceniami międzynarodowej organizacji ISO, które są obecnie wprowadzane w wielu krajach, także u nas. Przyzwyczajaj się powoli do tych nowych symboli. W trzeciej kolumnie znajdziesz dawne oznaczenia, spotykane w starszej literaturze.

Logika ujemna

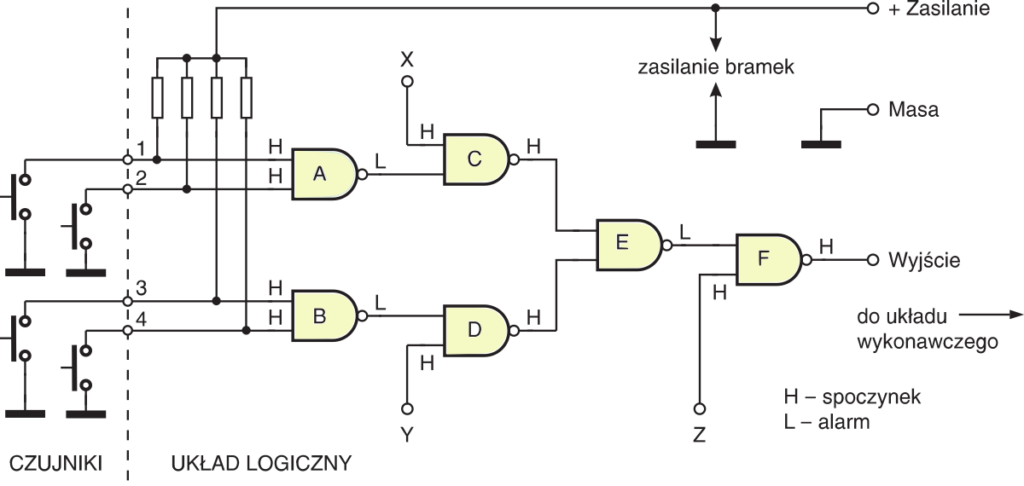
Popatrz teraz na układ pokazany na rysunku 5. Układ taki może być zastosowany w małej centralce alarmowej. Do czterech wejść oznaczonych 1…4 dołączone są czujniki. Wejście Z służy do całkowitego wyłączania centralki. Natomiast wejścia X, Y umożliwiają włączanie i wyłączanie pewnych stref (na przykład garaż powinien być chroniony w nocy także podczas obecności domowników). Naruszenie (zwarcie) któregokolwiek czujnika wywoła alarm, o ile tylko na wejściach zezwalających, oznaczonych X, Y, Z, będzie występował stan wysoki. W stanie gotowości (czuwania), w poszczególnych punktach układu wystąpią stany logiczne, takie jak podano na rysunku.

Zauważ, że jeśli naruszony zostanie przynajmniej jeden czujnik, zmieni się stan na wyjściu którejś z bramek oznaczonych A, B. Coś tu jakby nie gra: choć są to niewątpliwie bramki NAND, w rzeczywistości realizują funkcję OR lub NOR! Następne bramki, oznaczone C i D rzeczywiście realizują funkcję NAND − stan wyjścia zmienia się, gdy na wszystkich wejściach pojawi się stan wysoki. Ale bramka oznaczona E znów pełni jakby funkcję OR czy NOR − pojawienie się stanu niskiego na przynajmniej jednym jej wejściu zmienia stan wyjścia. Ostatnia bramka, oznaczona F, realizuje funkcję NAND − zmienia stan wyjścia, gdy na wszystkich wejściach wystąpi stan wysoki. Dokładnie to przeanalizuj. Coś nam tu przypomina opis działania bramki OR i NOR. Jak to rozumieć?

Do tej pory zakładaliśmy, zresztą całkowicie słusznie, że brak napięcia to stan niski − L, a obecność napięcia (dodatniego) to stan wysoki − H.

Ale przecież jest to kwestia umowy: równie dobrze moglibyśmy ustalić, że brak napięcia to stan wysoki, a obecność napięcia − stan niski. Tym sposobem doszliśmy do tak zwanej logiki ujemnej.

Jeśli zaglądałeś do podręczników omawiających technikę cyfrową, to istnieje duże prawdopodobieństwo, że jakiś niepoprawny teoretyk próbował ci namieszać w głowie, omawiając szczegółowo zarówno logikę dodatnią, jak i ujemną. Wydaje się to bardzo skomplikowane. Ta cała logika ujemna to prawda, ale praktykującemu elektronikowi może narobić w głowie sporo zamieszania i wtedy więcej z niej szkody niż pożytku.

Wyjaśniam więc raz na zawsze: we wszystkich praktycznych opisach i publikacjach z jakimi się spotkasz, a przede wszystkim w firmowych katalogach cyfrowych układów scalonych, stosuje się oznaczenia i pojęcia związane z logiką dodatnią, gdzie stan niski to napięcie bliskie zera, a stan wysoki to napięcie bliskie dodatniego napięcia zasilania. W zasadzie możesz więc nie zawracać sobie głowy logiką ujemną, ale koniecznie musisz zrozumieć pewne istotne zagadnienie, które dało o sobie znać przy analizie rysunku 5. Oto ono:

Zgodnie z tym, co pokazałem na rysunku 5 musisz zapamiętać, że dowolna bramka: AND, NAND, OR, NOR może pełnić zarówno swą „przepisową” funkcję, jak też funkcję niejako przeciwną.

Może jesteś zaskoczony: jak to jest, że ta sama bramka pełni funkcję AND i jednocześnie (tak!) funkcję OR? Teoretyk odpowie: tu właśnie wchodzi w grę logika ujemna. Nie przestrasz się tej logiki ujemnej, jest to bardzo proste − spróbuj wyczuć zagadnienie intuicyjnie.

Zauważ, że w układzie z rysunku 5 „prawdziwą” funkcję pełnioną przez bramki wyznaczają stany spoczynkowe na wejściach danej bramki. Nieprzypadkowo wcześniej do znudzenia wkładałem ci do głowy, że bramka AND i NAND „zmienia stan wyjścia, gdy wszystkie wejścia…”, natomiast bramka OR i NOR − „gdy przynajmniej jedno wejście…”. Przemyśl to i spróbuj zrozumieć. Nie radzę ci natomiast zapamiętywać jakichkolwiek tabelek, bo zaplączesz się beznadziejnie.

Dowolna bramka może w praktycznym układzie pełnić zarówno swą „przepisową” funkcję, jak też funkcję niejako przeciwną. W praktyce używając bramek jednego typu (ale muszą to być bramki z negacją) NOR, bądź NAND, możesz zrealizować wszystkie funkcje podstawowe: NOT, OR, NOR, AND, NAND, a także wszelkie funkcje złożone.

Ma to bardzo ważne konsekwencje praktyczne.

Niech do ciebie dotrze, że w układzie z rysunku 5 nie musieliśmy stosować bramek NOR czy OR − odpowiednio wykorzystaliśmy bramki NAND. Przeanalizuj rysunek 5 i upewnij się jeszcze raz, że w rzeczywistości bramki A, B i E pełnią w urządzeniu funkcje odpowiadające bramce NOR.

To, co ci teraz usiłuję wbić do głowy, jest ogromnie ważne w praktyce − jeśli uchwycisz ideę, będziesz potrafił zbudować dowolny układ, korzystając wyłącznie z bramek NAND lub NOR. Oczywiście musisz pomału nabrać wprawy.

Nie znaczy to jednak, że masz wykonywać układy zawierające tylko bramki NAND albo NOR. Bez przesady! Zachowaj rozsądek.

W każdym razie zrozumienie, a właściwie wyczucie i przyswojenie omówionych właśnie zasad, jest bardzo cenne przy projektowaniu urządzeń cyfrowych zawierających bramki. Szybko się o tym przekonasz, jeśli będziesz sam projektował układy. Może pomyślisz, że namawiam cię do czegoś wręcz przeciwnego, niż zalecają szkolne podręczniki. W wielu szkolnych ćwiczeniach masz za zadanie zrealizować daną wzorem funkcję logiczną przy użyciu dowolnych bramek. W praktyce najczęściej bywa zupełnie inaczej. Przy prostszych układach nikt nie zastanawia się nad wzorami, tylko od razu próbuje narysować schemat układu i na bieżąco zastanawia się, czy układ spełni postawione zadanie i jakich dostępnych kostek trzeba użyć.

Jeśli masz cierpliwość, weź teraz kartkę i narysuj jakiś niezbyt skomplikowany układ logiczny zawierający bramki: NOT, OR, NOR, AND i NAND. Potem spróbuj zrealizować układ pełniący takie same funkcje przy użyciu jednego typu bramek: NOR albo NAND.

Zakoduj sobie w głowie raz na zawsze, że każdą funkcję logiczną można zrealizować z pomocą bramek NAND czy też NOR. Używając odpowiednio dużej ilości takich bramek, teoretycznie mógłbyś wykonać dowolny przerzutnik, licznik, dekoder, a nawet mikroprocesor. Nie będziesz tego robił, bo wcześniej zrobili to za ciebie inni i masz do dyspozycji wiele cyfrowych układów scalonych pełniących najróżniejsze funkcje. Układy te zacznę ci przedstawiać w jednym z następnych odcinków. Wykaż cierpliwość: zanim przejdziemy do przerzutników, liczników, rejestrów i dekoderów, wcześniej musisz przyswoić sobie sporo rzetelnej wiedzy.

Jeśli zajmujesz się techniką cyfrową, powinieneś o każdej porze dnia i nocy pamiętać, jak działają bramki: NOT, OR, NOR, AND, NAND, EX−OR i EX−NOR. Musisz dokładne rozumieć działanie bramki jako sterowanego zaworu. Powinieneś rozumieć dlaczego każda bramka NAND czy AND umożliwia zrealizowanie funkcji NOR i OR, i jakie to ma znaczenie praktyczne. Nie bój się logiki ujemnej − to nic trudnego; pamiętaj, że o rzeczywistej funkcji bramki decydują stany na jej wejściach podczas „spoczynku”. Nie ucz się żadnych tabelek − staraj się zrozumieć zasady. W razie potrzeby przygotuj sobie ściągawkę zawierającą podstawowe informacje.

A w następnym odcinku zajmiemy się budową wewnętrzną współczesnych bramek i innych układów cyfrowych oraz praktycznymi konsekwencjami różnic w ich budowie.

Piotr Górecki