Poznajemy elementy indukcyjne – część 3

W dwóch poprzednich odcinkach próbowałem  wytłumaczyć Ci działanie elementów elektronicznych, w szczególności cewek indukcyjnych na przykładzie urządzeń hydraulicznych. Dziś dalsze zagadnienia. Ponieważ temat nie jest łatwy, być może będziesz musiał przeczytać materiał kilkakrotnie, aby zrozumieć i przyswoić sobie podane zasady.

Wiesz już, że cewka przeciwstawia się zmianom prądu (a kondensator − zmianom napięcia). Rozumiesz, że przy zmianach prądu, w cewce wytwarza się napięcie, zwane napięciem samoindukcji. Napięcie to może mieć wartość wielokrotnie przekraczającą wartości napięć zasilania układu, w którym dana cewka pracuje.

Wiesz, że w obwodach prądu zmiennego cewki i kondensatory stawiają przepływającemu prądowi pewien opór, zwany reaktancją. Opór ten zależy od częstotliwości − w cewkach, ze wzrostem częstotliwości opór ten rośnie, w kondensatorach − maleje. Dziś zajmiemy się dalszymi zagadnieniami z tej dziedziny.

Rezonans

Ze słowem rezonans na pewno się już spotkałeś. Zapoznajmy się z rezonansem w obwodach elektrycznych. Jak zwykle, najpierw spróbujemy znaleźć łatwiejszą do zrozumienia, hydrauliczną analogię.

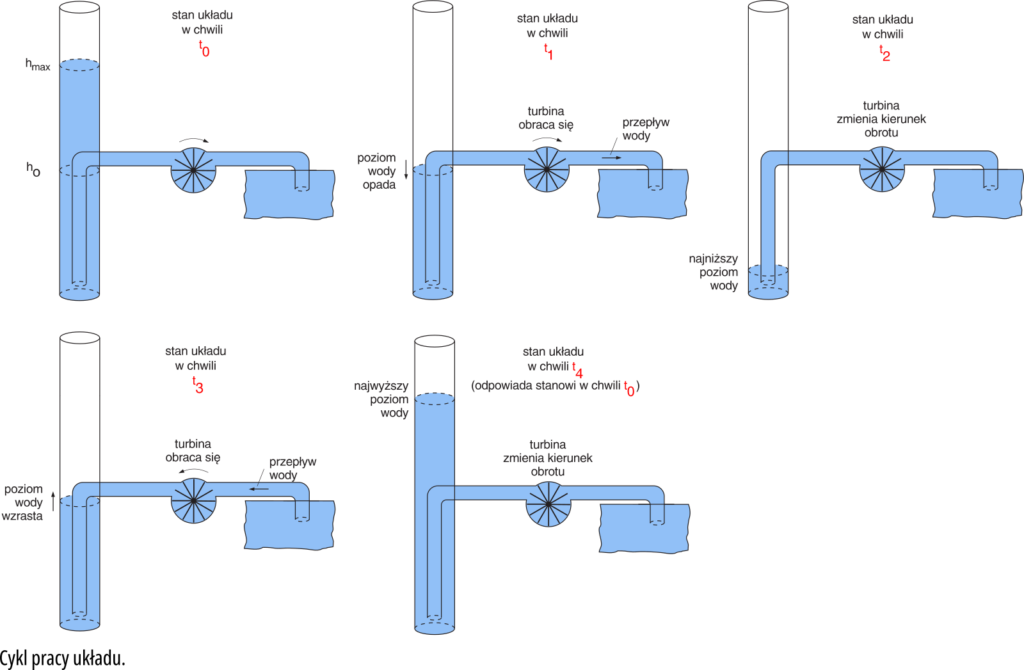
Spójrz na rysunek 1. Zobaczysz wysoką, pionową rurę, otwartą od góry i turbinę bierną z kołem zamachowym. Jak pamiętasz, rura jest odpowiednikiem kondensatora, turbina − odpowiednikiem cewki.

Załóżmy, że w stanie początkowym, czyli do chwili nazwanej t₀, zawór jest zamknięty i poziom wody w rurze jest wyższy od poziomu zerowego − jest to poziom oznaczony h_max. Gdy w chwili t₀ zawór zostanie otwarty, poziom wody w rurze zacznie się obniżać. Turbina bierna zacznie się obracać i będzie nabierać prędkości. W pewnej chwili (nazwijmy ją chwilą t₁), poziom wody w rurze obniży się do poziomu zerowego, oznaczonego h₀. Na pierwszy rzut oka mogłoby wyglądać, że w chwili t₁, czyli w momencie wyrównania poziomu wody w rurze z poziomem wody w dużym zbiorniku, przepływ wody ustanie. Owszem, w końcu ustanie, ale jeszcze nie teraz! Przecież przepływ wody przez turbinę w czasie od chwili t₀ do t₁ spowodował, że nabrała ona prędkości. W jej kole zamachowym zgromadziła się jakaś ilość energii. Dzięki tej energii, po chwili t₁ turbina będzie spełniać rolę pompy i spowoduje dalsze obniżanie poziomu wody w rurze, poniżej poziomu h₀. Poziom wody w rurze będzie się więc nadal obniżał, a turbina tracić będzie stopniowo swą energię na wypompowanie wody i jej obroty będą coraz wolniejsze. W pewnej chwili t₂, poziom wody w rurze będzie najniższy (h_min) i turbina się zatrzyma. Oczywiście zaraz potem turbina zacznie obracać się w przeciwnym kierunku, a poziom wody w rurze zacznie wzrastać. W chwili t₃ poziom wody w rurze zrówna się z poziomem wody w dużym zbiorniku, ale przepływ wody nie ustanie, bo w czasie od t₂ do t₃ turbina zdąży nabrać prędkości i po chwili t₃ znów będzie pełnić rolę pompy. Poziom wody w rurze będzie więc nadal wzrastał i w chwili t₄ osiągnie poziom najwyższy. Oczywiście w chwili t₄ turbina na moment się zatrzyma, a zaraz potem zacznie się obracać w przeciwnym kierunku. Zauważ, że w chwili t₄ stan układu jest taki jak w chwili t₀. A więc opisany cykl powtórzy się, i to nie raz.

Poszczególne fazy takiego cyklu pokazane są na rysunku 2.

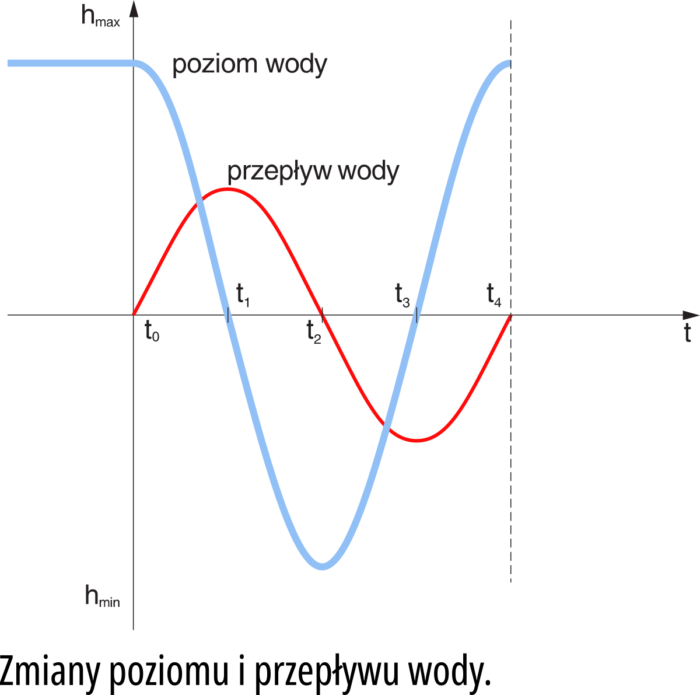
Natomiast na rysunku 3 możesz zobaczyć, jak zmienia się poziom wody w rurze oraz przepływ wody (co odpowiada prędkości turbiny).

Patrząc na zjawisko ze strony energetycznej, można powiedzieć, że energia zgromadzona pierwotnie w rurze (jako energia potencjalna słupa wody), zostaje przekazana do turbiny (gdzie gromadzi się w postaci energii kinetycznej koła zamachowego). Potem znów jest gromadzona jako energia potencjalna słupa wody, itd, itd. W układzie zachodzi więc proces ciągłego przekazywania (wymiany) energii między rurą a turbiną.

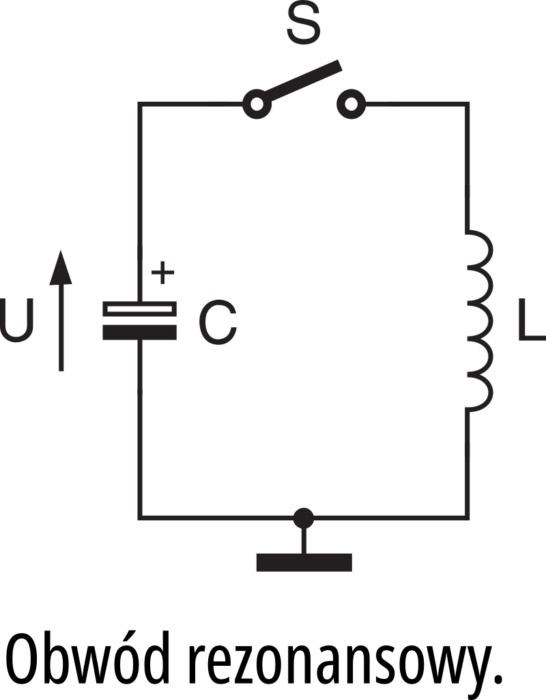
A teraz popatrz na rysunek 4. Nie masz chyba wątpliwości, że przedstawia on elektryczną analogię układu z rysunku 1. To właśnie jest obwód rezonansowy. Jego działanie dokładnie odpowiada przedstawionemu wcześniej opisowi, przy czym napięcie na kondensatorze odpowiada poziomowi wody w rurze, a prąd − przepływowi wody. Jak się słusznie domyślasz, rysunek 3 pokazuje także przebieg prądu w obwodzie i napięcia na kondensatorze.

Czy zauważyłeś, że na początku, przed chwilą t₀, mieliśmy stan ustalony − na kondensatorze występowało stałe napięcie dodatnie. Po zamknięciu wyłącznika S, stało się coś dziwnego − w obwodzie pojawiły się przebiegi przemienne. Co ciekawe, są to przebiegi o kształcie sinusoidy. A więc zrobiliśmy coś na kształt generatora przebiegów sinusoidalnych. To nie jest przypadek. Połączenie cewki (L) i kondensatora (C) daje obwód rezonansowy, który zawsze ma związek z przebiegami sinusoidalnymi. Możemy obrazowo powiedzieć, że każdy obwód rezonansowy „lubi” pewną częstotliwość. Dla konkretnej cewki i konkretnego kondensatora będzie to jakaś częstotliwość charakterystyczna, zwana częstotliwością rezonansową obwodu.

A od czego zależy częstotliwość tak wytwarzanych drgań? Popatrz na rysunki 1 i 2, pomyśl chwilę i odpowiedz!

Czy jesteś przekonany, że częstotliwość będzie zależeć od pojemności rury i od bezwładności koła zamachowego turbiny?

Oczywiście, jeśli pojemność rury będzie mała i bezwładność turbiny też będzie mała, to zmiany będą szybkie, czyli częstotliwość drgań duża. I odwrotnie, gdy pojemność i bezwładność będą duże, wtedy zmiany będą powolne, czyli częstotliwość będzie mała.

Tak samo jest z obwodem elektrycznym LC. Czym większa pojemność i indukcyjność, tym mniejsza częstotliwość. Zapamiętaj bardzo ważny wzór. Jest to wzór na częstotliwość rezonansową obwodu LC:

gdzie frez − częstotliwość rezonansowa, L − indukcyjność, a C − pojemność. W praktyce dla częstotliwości radiowych zazwyczaj podaje się indukcyjność w mikrohenrach, a pojemność w pikofaradach. Wtedy częstotliwość wyraża się w megahercach. Natomiast dla małych częstotliwości indukcyjność podaje się w milihenrach, pojemność w nanofaradach w tym przypadku częstotliwość wyraża się w kilohercach. Częstotliwość rezonansową można też obliczyć za pomocą prostszego, przekształconego wzoru:

f w MHz, L w μH, C w pF lub f w kHz, L w mH, C w nF.

Co ciekawe, dla częstotliwości rezonansowej, reaktancja cewki (XL=2πfL) jest równa liczbowo reaktancji kondensatora (XC=1/2πfC). Zapamiętaj to raz na zawsze:

rezonans występuje zawsze wtedy, gdy reaktancja cewki jest liczbowo równa reaktancji kondensatora.

Teraz już z grubsza wiesz, co to jest i jak działa obwód rezonansowy.

Rezystancja charakterystyczna

Popatrz jeszcze raz na rysunki 1, 3 i 4. Załóżmy, że w stanie ustalonym, czyli przed chwilą t₀, poziom wody w rurze wynosi h_max (napięcie na kondensatorze − U_max). Co możemy powiedzieć o maksymalnej wielkości przepływu wody (natężenia prądu) po chwili t₀? Co się stanie, jeśli zmniejszymy bezwładność turbiny (zmniejszymy indukcyjność)?

Zastanów się… Co wymyśliłeś?

Na pewno zmieni się szybkość zmian, czyli wzrośnie częstotliwość drgań − zgadza się to z podanym wcześniej wzorem na częstotliwość rezonansową. Ale nas interesuje wartość prądu. Odpowiedź możemy uzyskać na kilka sposobów:

Wiemy, ze cewka przeciwstawia się zmianom prądu. Cewka o mniejszej indukcyjności przeciwstawia się słabiej, czyli prąd jest większy.

Podchodząc ze strony energetycznej, wyciągamy taki sam wniosek − pamiętamy, że między kondensatorem i cewką występuje ciągłe przekazywanie energii. Jeśli ta sama ilość energii kondensatora ma w krótszym czasie zostać przekazana do cewki (cewki o mniejszej indukcyjności), to prąd musi być większy. To samo wychodzi nam ze znanych wzorów:

Jak z tego widać, możemy tu mówić o swego rodzaju oporności: to samo napięcie wywołuje przepływ prądu o różnej wartości.

Ponieważ jest to bardzo ważna, a często zupełnie nie rozumiana sprawa. Przyjrzyjmy się jej jeszcze dokładniej.

Wyobraź sobie, że masz trzy obwody rezonansowe o podanych niżej wartościach elementów:

L=1H i C=1nF
L=1mH i C=1μF
L=1μH i C=1mF.

Zauważ, że wszystkie mają tę samą częstotliwość rezonansową.

Ale chyba czymś się różnią?

Wytłumacz mi, proszę, czym różnią się te trzy obwody rezonansowe o podanych wartościach elementów. Wróć do rysunku 1 i zastanów się, co to naprawdę oznacza. Zanim przeczytasz poniższy akapit spróbuj wyciągnąć wnioski samodzielnie.

A teraz analizujemy wspólnie.

Przypadek pierwszy: duża indukcyjność (1H), mała pojemność (1nF). Odpowiada to cienkiej rurze i ciężkiej turbinie. Przy danym napięciu U_max w małym kondensatorze zgromadzi się niewielka ilość energii. Przy dużej indukcyjności prąd będzie bardzo mały.

Zauważ − przy danym napięciu U_max uzyskujemy mały prąd.

W trzecim przypadku, przy danym napięciu U_max, w kondensatorze o dużej pojemności zgromadzi się znaczna ilość energii. Przy małej wartości indukcyjności, prąd będzie duży. Odpowiada to grubej rurze i lekkiej turbinie.

Co możemy powiedzieć o zależności prądu od napięcia? Widać tu jasno, że z obwodem rezonansowym związana jest jakaś wartość oporności charakterystycznej. Tę oporność charakterystyczną oznacza się zazwyczaj grecką literką ρ.

Co to za oporność? Musisz to zrozumieć dokładnie, żeby Ci się wszystko nie pomieszało − wiedz, że niebawem będziemy mówić o innych rodzajach oporności, z wiązanych z obwodem rezonansowym.

Może powiesz, że to było dla Ciebie jasne od początku − przecież cały czas chodzi tu o reaktancję elementów przy częstotliwości rezonansowej. Masz rację i ma to ważne znaczenie praktyczne. Możesz znaleźć tę oporność charakterystyczną licząc częstotliwość rezonansową, a potem reaktancje. Oczywiście:

Łatwiej jednak skorzystać z prostego wzoru:

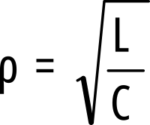
Ten wzór już pewnie gdzieś widziałeś. Jaki jest jednak jego sens praktyczny.

Po pierwsze − oporność charakterystyczna obwodu rezonansowego jest równa reaktancji cewki i równa reaktancji kondensatora przy częstotliwości rezonansowej.

Po drugie ma to związek z tak zwanym dopasowaniem i przekazywaniem energii. To jest zagadnienie ogromnie ważne w technice w.cz. − zajmiemy się nim trochę później.

Tłumienie drgań

Z rysunku 3 mogłoby wynikać, że w chwili t₄ sytuacja jest identyczna, jak w chwili t₀. To by znaczyło, że drgania będą utrzymywać się w nieskończoność. Czy tak może być? Jak myślisz?

Odpowiedz!

Jeśli odpowiedziałeś, że drgania mogłyby utrzymywać się w nieskończoność, pod warunkiem, że nie występowałyby żadne straty, masz rację!

W praktyce, w układzie hydraulicznym będą jednak występować straty wywołane tarciem: zarówno w turbinie, jak i w rurach połączeniowych. Czym mniejsze będą te straty, tym dłużej utrzymają się drgania.

W rzeczywistym układzie elektrycznym też zawsze występują jakieś straty. Większość tych strat spowodowanych jest rezystancją cewki. Prawdziwa cewka składa się z pewnej ilości zwojów drutu. Drut ten ma jakąś niezerową rezystancję. Ponadto przy dokładnym rachunku należałoby uwzględnić rezystancję przewodów łączeniowych i różnego typu strat w kondensatorze. W praktyce zdecydowanie największe są straty na rezystancji cewki, i pozostałe straty można spokojnie pominąć.

Narysujmy więc praktyczny schemat zastępczy obwodu rezonansowego. Schemat taki możesz zobaczyć na rysunku 5.

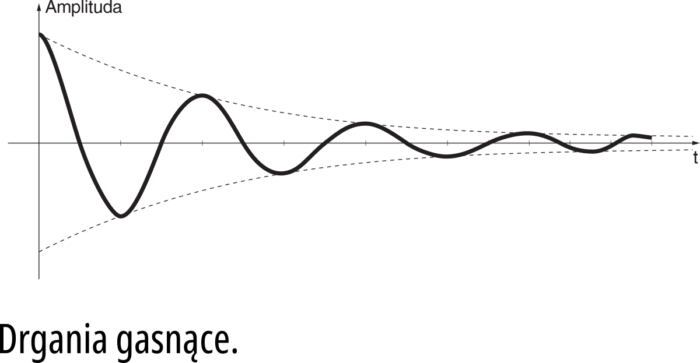
W rzeczywistości przebiegi prądu i napięcia nie będą więc wyglądać, jak na rysunku 3. W każdym cyklu część energii jest bezpowrotnie tracona (zamieniana w procesie tarcia w bezużyteczne ciepło). Tak samo jest w obwodzie elektrycznym. Dlatego kolejne drgania będą mieć coraz mniejszą amplitudę. W rzeczywistości przebiegi napięcia i prądu w obwodzie rezonansowym będą drganiami gasnącymi − pokazuje to rysunek 6. Czym większe będą straty, tym szybciej zanikną drgania. Można powiedzieć, że rezystancja występująca w obwodzie rezonansowym tłumi drgania.

Choć trzeba rozumieć podaną właśnie przyczynę zaniku drgań w obwodzie rezonansowym, w praktyce ważniejsze są inne objawy tego zjawiska. O tym jednak później.

W tym miejscu dla ścisłości należałoby wyjaśnić kwestię, czy rezystancja strat wpływa na częstotliwość rezonansową. Jeszcze raz przeanalizuj rysunek 5. Jeśli dojdziesz do wniosku, że rezystancja ma tu jakiś wpływ − masz rację. Ale przy niewielkich stratach wpływ na częstotliwość jest wręcz pomijalnie mały, dlatego prawie nigdy nie uwzględnia się jej przy obliczaniu częstotliwości rezonansowej. Warto jednak wiedzieć, że znany wzór:

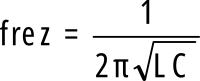
w zasadzie dotyczy obwodu idealnego. Nie ma to znaczenia − w praktyce i tak obliczenia dokładne nie są potrzebne, bo rzeczywiste cewki i kondensatory wykonywane są z pewną niezerową tolerancją i dla uzyskania potrzebnej częstotliwości trzeba stosować strojenie obwodu przez zmianę indukcyjności lub pojemności.

Czwarta część cyklu znajduje się tutaj.

Piotr Górecki