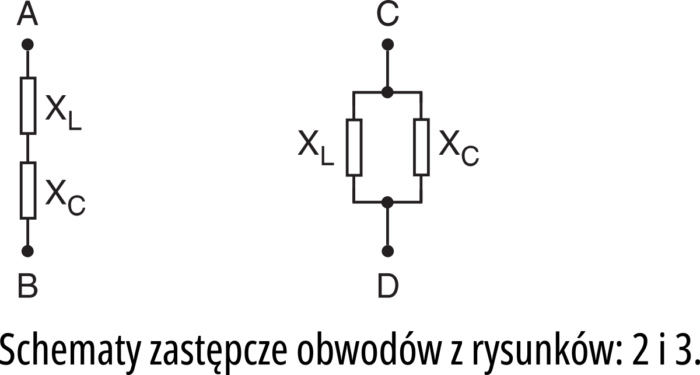Poznajemy elementy indukcyjne – część 4
W tej części kontynuujemy rozważania dotyczące obwodu rezonansowego, które zaczęliśmy analizować w poprzednim odcinku. Ważnym pojęciem, które pojawia się w tym artykule, jest pojęcie dobroci obwodu.
Dobroć obwodu rezonansowego
Mówiliśmy już, że w każdym rzeczywistym obwodzie rezonansowym występują straty. Straty te możemy przedstawić w postaci rezystancji włączonej szeregowo z indukcyjnością (niewielkie straty kondensatora pomijamy). Gdybyśmy chcieli, moglibyśmy też włączyć w obwód rezonansowy dodatkową rezystancję szeregową. Oczywiście włączenie takiej rezystancji dodatkowo zwiększy straty, czyli bardziej stłumi obwód.
Potrzebna byłaby nam jakaś miara tych strat.
Spójrzmy na problem od strony energetycznej. W czasie rezonansu następuje cykliczna wymiana (przepływ) energii między cewką a kondensatorem. W każdym cyklu drgań (okresie), tracona jest jakaś część energii zgromadzonej w obwodzie. Zauważ, że stosunek całkowitej energii gromadzonej w elementach obwodu do energii strat (w ciągu jednego okresu) nie zależy od napięcia pracy. Czym większe napięcie, tym większy prąd i większe straty w rezystancji.
Wprowadźmy więc pojęcie dobroci, jako miary tych strat. Dobroć oznacza się dużą literą Q.
Nie będę Ci oczywiście wyprowadzał wzoru − podam tylko końcowy wynik:
![]()
gdzie Rs to zastępcza szeregowa rezystancja strat, którą zaznaczyliśmy na rysunku 5 w poprzedniej części, zaś ρ to rezystancja charakterystyczna.
Jak wynika z wcześniejszych wzorów:
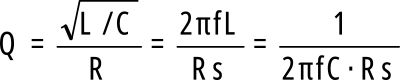
Ty pewnie w literaturze spotkałeś inne określenie dobroci. My dojdziemy do tego później. Choć w praktyce rzeczywiście mówi się o dobroci nieco w innym kontekście (chodzi o szerokość pasma filtru), Ty zawsze pamiętaj, że dobroć w swych korzeniach jest miarą strat w obwodzie.
Tu należałoby już przejść do obwodu rezonansowego jako filtru. Zanim to zrobimy, musisz jeszcze utrwalić sobie pewne istotne wiadomości i wyobrażenia związane z rezonansem.
Obwód rezonansowy jako filtr
Chyba nie masz wątpliwości, że bardzo rzadko wykorzystujemy obwód rezonansowy do wytwarzania drgań gasnących według rysunku 4 w poprzedniej części. Narysowałem Ci go tylko dla ułatwienia analizy. Do czego więc przydaje się obwód rezonansowy?
Przed chwilą mówiłem Ci, że obwód rezonansowy lubi swoją częstotliwość rezonansową.
Najogólniej biorąc, idealny (czyli bezstratny) obwód rezonansowy „lubi” swoją częstotliwość rezonansową niezmiernie − „lubi” ją tak bardzo, że potrafi ją wytworzyć niejako z niczego, a właściwie z napięcia stałego; co więcej − utrzyma drgania w nieskończoność. Jeśli w obwodzie występuje rezystancja strat, jego „miłość” do częstotliwości rezonansowej jest mniejsza − tym mniejsza, im większe straty.
Już na pierwszy rzut oka widać, że obwód rezonansowy wyróżnia swoją „ulubioną” częstotliwość, więc może być wykorzystany do filtrowania, czyli oddzielania przebiegów o różnych częstotliwościach.
Przyjrzyjmy się temu dokładniej.
Rezonans równoległy i rezonans szeregowy
Niejednokrotnie spotkałeś już określenia: obwód rezonansowy równoległy i szeregowy. Prawdopodobnie też słyszałeś o czymś takim jak rezonans prądów i rezonans napięć. Czyżby więc istniały dwa rodzaje rezonansu?
Nie. Określenia te wzięły się z praktyki − ze sposobu wykorzystania obwodu rezonansowego. O nazwie decyduje sposób dołączenia współpracujących z obwodem elementów, zwłaszcza rezystancji.
Ponieważ nie omawialiśmy jeszcze pojęcia źródła prądowego i nie chcę Cię męczyć wprowadzeniem pojęcia przewodności (odwrotności rezystancji), muszę Ci sprawę uzmysłowić trochę okrężną drogą.
Na rysunku 4 w poprzedniej części mieliśmy do czynienia z obwodem idealnym, bezstratnym. Niewiele myśląc, rezystancję reprezentującą straty włączyliśmy w obwód szeregowo. W zasadzie jest to jak najbardziej słuszne. W układzie hydraulicznym z rysunku 1 w poprzedniej części, straty wynikają głównie z tarcia wody o rury i tarcia w turbinie. Rzeczywiście, aż prosi się, aby straty te w układzie hydraulicznym przedstawić w postaci zwężki, umieszczonej szeregowo, a w obwodzie elektrycznym w postaci szeregowego rezystora.
Ale pomyśl chwilę − czy tych strat nie można przedstawić inaczej?
Dlaczego nie przedstawić ich jako rezystancji równoległej?
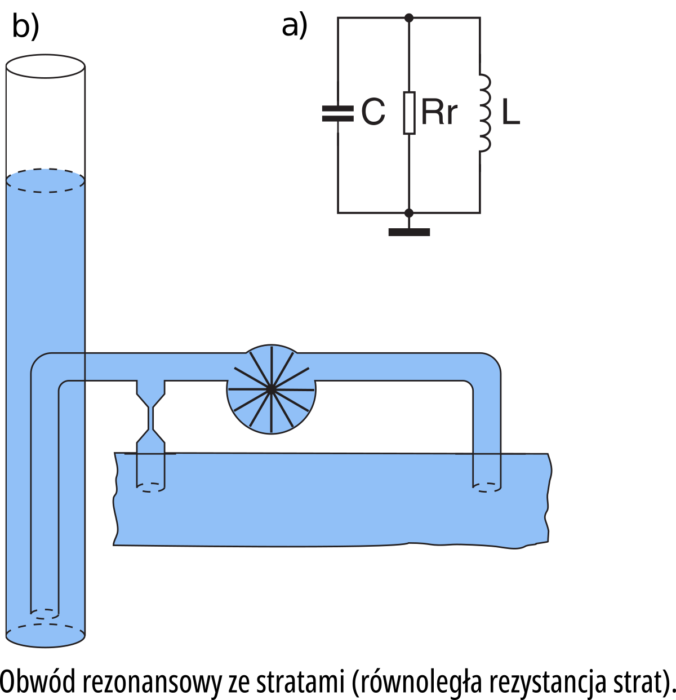
W układzie w elektrycznym wyglądałoby to jak na rysunku 1a, a w hydraulicznym jak na rysunku 1b (porównaj to z rysunkiem 5 w poprzedniej części).
Zastanów się − w rzeczywistości straty powstają we wszystkich elementach rzeczywistego układu − w dielektryku kondensatora, w doprowadzeniach kondensatora, w przewodach łączących, w drucie cewki, w rdzeniu cewki itd. My przy opisie sytuacji musimy przedstawić je w jakiś prosty sposób (w postaci jednej, zastępczej rezystancji), żeby zbytnio nie komplikować obliczeń i analizy. Powinniśmy mieć przy tym świadomość, że nasz opis na pewno jest lepszym lub gorszym przybliżeniem. Jeśli tak, to nie ma większej różnicy, czy straty w obwodzie rezonansowym przedstawimy w postaci szeregowej, czy równoległej. Przedstawimy tak, żeby nam było wygodniej i łatwiej liczyć oraz analizować zachowanie układu.
Popatrz jeszcze na rysunek 1 i rysunek 5 w poprzedniej części . Odpowiedz na pytanie kontrolne: czy dla konkretnego obwodu, zastępcza szeregowa rezystancja strat ma taką samą wartość jak zastępcza równoległa rezystancja strat?
Oczywiście, że nie − w dobrym obwodzie rezonansowym straty są w sumie niewielkie. Czyli rezystancja szeregowa z rysunku 5 w poprzedniej części będzie miała wartość niewielką, a równoległa z rysunku 1a − bardzo dużą.
Może jeszcze zapytasz, jak to jest z dobrocią przy przedstawieniu strat w postaci rezystancji równoległej?
Przed chwilą doszliśmy do wniosku, że równoległa rezystancja ma dużą wartość. Zapewne nie zaskoczy Cię więc wzór na dobroć w obwodzie równoległym:
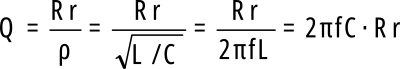
Zauważ, czym różni się on od wcześniej podanego dla rezystancji szeregowej:
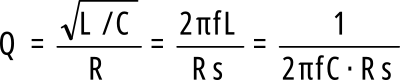
Oczywiście dla danego obwodu z obu wzorów musi wyjść ta sama wartość dobroci. Inaczej być nie może. Przecież dobroć nie bierze się ze wzorów − wprost przeciwnie, to my dobieramy jakieś modele i jakieś wzory, które mają możliwie wiernie opisywać rzeczywiste zjawiska, z jakimi mamy do czynienia w obwodzie rezonansowym. Zapamiętaj ważną regułę:
Sumę strat w obwodzie rezonansowym możemy przedstawić jako zastępczą rezystancję strat. Dla wygody i ułatwienia obliczeń, rezystancja taka może być włączona do obwodu szeregowo albo równolegle.
Jeśli mamy już dwa schematy zastępcze obwodu rezonansowego, robimy kolejny ważny krok.
Oporność obwodu rezonansowego
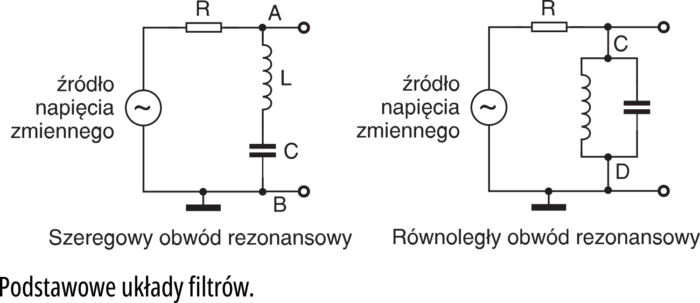
Na rysunku 2 możesz zobaczyć dwa podstawowe filtry, wykorzystujące obwód rezonansowy. Są one często spotykane w praktyce, zwłaszcza w technice w.cz. Właśnie tu masz szeregowy i równoległy obwód rezonansowy. Na początek interesować nas będzie oporność, jaką dla różnych częstotliwości stanowi obwód rezonansowy.
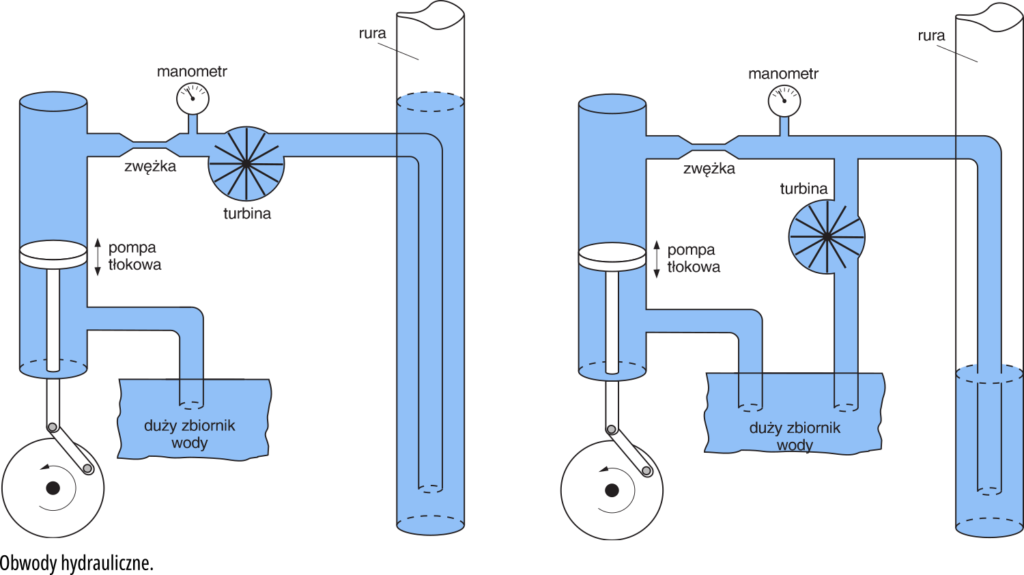
Żeby to lepiej zrozumieć, spróbujmy z grubsza przeanalizować działanie układów hydraulicznych pokazanych na rysunku 3.
Najpierw zastanówmy się wspólnie nad działaniem układu z rysunku 3a, który ma przybliżyć działanie układu elektrycznego z rysunku 2a. Dla bardzo małych częstotliwości (bardzo wolnych ruchów tłoka pompy), turbina będzie się powoli obracać w jedną i w drugą stronę, a poziom wody w rurze będzie się pomału podnosił i opadał w takt ruchów tłoka.
Skoncentruj się. Czy zauważyłeś, że przy tak małej częstotliwości obecność turbiny praktycznie nie ma znaczenia i układ zachowuje się, jakby składał się tylko z pompy, zwężki i rury. Z kolei dla bardzo dużych częstotliwości, przede wszystkim daje o sobie znać bezwładność turbiny. Turbina praktycznie się nie porusza. Dla dużych częstotliwości obecność rury praktycznie nie ma znaczenia, bo turbina skutecznie oddziela rurę od pompy i zwężki − układ zachowuje się tak, jakby składał się tylko z pompy, zwężki i turbiny.
Prześledźmy działanie układu z rysunku 3b. Dla bardzo małych częstotliwości turbina obraca się bez przeszkód w jedną i drugą stronę. Jakiekolwiek (powolne) zmiany ciśnienia powodują przepływ wody przez turbinę. Tym samym obecność rury nie gra praktycznie żadnej roli − układ zachowuje się, jakby składał się tylko z pompy, zwężki i turbiny. Z kolei przy bardzo dużych częstotliwościach ciężka turbina praktycznie nie przepuszcza wody w żadnym kierunku − układ zachowuje się tak, jakby składał się tylko z pompy, zwężki i rury.
Analogicznie wygląda to w obwodzie elektrycznym. Spróbuj zrozumieć (nie musisz natomiast uczyć się na pamięć):
1.obwód rezonansowy szeregowy
− dla małych częstotliwości zachowuje się jak kondensator (ma charakter pojemnościowy)
− dla dużych częstotliwości zachowuje się jak cewka (ma charakter indukcyjny)
2.obwód rezonansowy równoległy zachowuje się odwrotnie:
− dla małych częstotliwości zachowuje się jak cewka (ma charakter indukcyjny)
− dla dużych częstotliwości zachowuje się jak kondensator (ma charakter pojemnościowy).
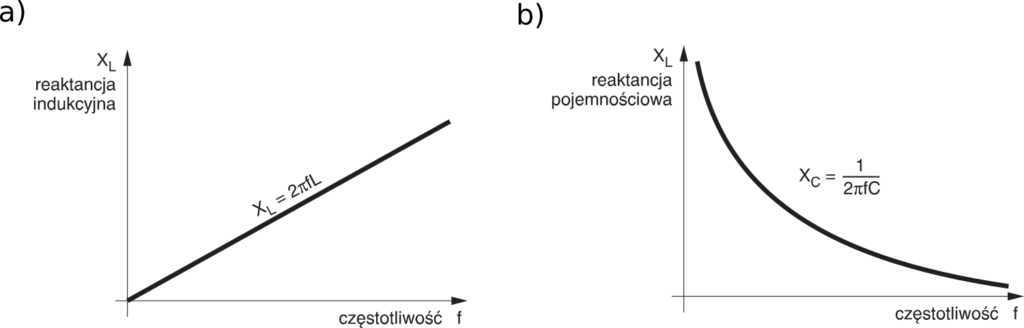
Zanim dowiesz się, jak to wygląda dla częstotliwości rezonansowej, utrwal sobie podane wyżej informacje, korzystając z rysunku 4. Właśnie na rysunku 4a i 4b możesz zobaczyć, jak zmienia się reaktancja cewki i kondensatora przy zmianach częstotliwości.
Teraz popatrz na rysunek 2a. Mamy tu szeregowe połączenie cewki i kondensatora. Natomiast na rysunku 2b mamy równoległe połączenie tych elementów. Wiemy, że reaktancja jest swego rodzaju opornością. Rysujemy więc schemat zastępczy szeregowego i równoległego obwodu rezonansowego − patrz rysunek 5. Z połączeniem oporów chyba nie powinniśmy mieć kłopotów.
Zastanów się:
Przy połączeniu szeregowym, wypadkowa oporność powinna być sumą obu oporności składowych. Zgadza się to z podanymi przed chwilą wnioskami: szeregowy obwód rezonansowy dla małych częstotliwości ma charakter pojemnościowy, bo reaktancja kondensatora ma wartość dużo większą niż reaktancja cewki. Tak samo przy dużych częstotliwościach dominuje reaktancja indukcyjna. Wszystko pasuje.
Przy połączeniu równoległym wypadkowa oporność powinna być mniejsza od każdej z oporności składowych. Tak przynajmniej jest przy łączeniu rezystorów. Na pierwszy rzut oka w równoległym obwodzie rezonansowym też tak jest: przy małych częstotliwościach obwód ten ma małą reaktancję − decyduje o tym mała reaktancja cewki, natomiast reaktancja kondensatora jest duża, więc nie ma istotnego wpływu na wypadkową reaktancję.
Dla dużych częstotliwości obwód równoległy też ma małą reaktancję − tym razem decydujące znaczenie ma mała reaktancja kondensatora, a dużą reaktancję cewki można zaniedbać.
Wszystko wydaje się jasne. Może więc spróbujemy narysować przebieg reaktancji obwodu równoległego i szeregowego w zależności od częstotliwości.
Biorąc pod uwagę zasady obowiązujące przy łączeniu rezystorów narysowalibyśmy krzywe wypadkowe, jak na rysunku 6.
Jednak w rzeczywistości oporność wypadkowa obwodów rezonansowych wcale nie zmienia się tak, jak na rysunku 6, dlatego rysunek jest przekreślony. Dla obwodów rezonansowych, w których straty związane z występowaniem szkodliwych rezystancji są bardzo małe, oporność wypadkowa będzie taka, jak na rysunku 7.
Czy jesteś zdziwiony?
Okazuje się, że dla częstotliwości rezonansowej idealny obwód szeregowy ma oporność równą zeru. Natomiast obwód równoległy stanowi wtedy nieskończenie wielką rezystancję.
Nietrudno się domyślić, że straty jakby pogarszają sytuację.
Skoncentruj się. Czy już potrafiłbyś odpowiedzieć na pytanie, jakie będą wypadkowe oporności odwodu w stanie rezonansu?
Popatrz na wzory na dobroć obwodu równoległego i szeregowego:
![]()
![]()
Przekształć je:
Rr = ρ⋅Q
![]()
Uważaj! Masz tu odpowiedź, jakie oporności będzie miał szeregowy, a jakie równoległy obwód rezonansowy.
Zapamiętaj więc raz na zawsze:
Idealny obwód szeregowy miałby w rezonansie oporność równą zeru.
Idealny obwód równoległy miałby w rezonansie oporność nieskończenie wielką.
Przy praktycznych obliczeniach rzeczywistych obwodów rezonansowych nie znamy wartości Rs i Rr, znamy za to indukcyjność L , pojemność C i umiemy w stosunkowo prosty sposób zmierzyć dobroć Q. Punktem wyjścia do obliczenia Rs i Rr jest rezystancja charakterystyczna:
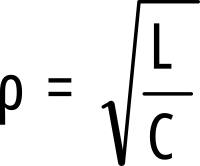
Dla częstotliwości rezonansowej szeregowe połączenie cewki i kondensatora (obwód szeregowy) ma minimalną oporność Rs, Q− krotnie mniejszą od rezystancji charakterystycznej ρ.
Natomiast obwód równoległy ma przy częstotliwości rezonansowej oporność Rr Q− krotnie większą od rezystancji charakterystycznej ρ.
Inaczej mówiąc, znaleźliśmy praktyczny sens wprowadzonych poprzednio zastępczych rezystancji Rs i Rr. Właśnie takie oporności, a ściślej biorąc − rezystancje, ma obwód równoległy i szeregowy w rezonansie.
Masz teraz komplet informacji, bo wcześniej przeanalizowaliśmy, jaką oporność reprezentuje obwód rezonansowy dla częstotliwości większych i mniejszych od rezonansowej.
Zapewne wiesz już, jak będą działać filtry, pokazane na rysunku 2.
Biorąc pod uwagę przebieg oporności obwodu rezonansowego w funkcji częstotliwości z rysunku 7, dojdziesz do wniosku, że filtr z obwodem równoległym z rysunku 2b przepuszcza częstotliwości zbliżone do swojej częstotliwości rezonansowej. Filtr z obwodem szeregowym przepuszcza wszystkie inne, a stanowi pułapkę dla częstotliwości bliskich częstotliwości rezonansowej.
W następnym odcinku przyjrzymy się bliżej sprawie łączenia oporności i pomału doprowadzę Cię do liczb zespolonych.
Piotr Górecki