Poznajemy elementy indukcyjne – część 5

W poprzednim odcinku zacząłem Ci tłumaczyć sprawę rezonansu. Poznałeś pojęcie oporności charakterystycznej − jest to występująca podczas rezonansu oporność cewki i równa jej liczbowo oporność kondensatora. Doszliśmy do wniosku, że w idealnym obwodzie rezonansowym powstałe drgania mogłyby się utrzymywać w nieskończoność.

Omówiliśmy pojęcie dobroci jako miary strat w obwodzie nieidealnym. Zaczęliśmy analizować działanie szeregowego i równoległego obwodu rezonansowego − okazało się, że obwód rezonansowy działa jak filtr. Ostatnio wzięliśmy na warsztat sprawę oporności wypadkowej szeregowego i równoległego obwodu rezonansowego.

Wiesz już, że dla częstotliwości rezonansowej szeregowe połączenie cewki i kondensatora (obwód szeregowy) ma minimalną oporność − stanowi rezystancję Q−krotnie mniejszą od rezystancji charakterystycznej (gdzie ρ = √(L/C) ). W obwodzie idealnym, bezstratnym, oporność ta wynosiłaby zero.

Natomiast obwód równoległy ma przy częstotliwości rezonansowej oporność, a ściślej − rezystancję, o wartości Q−krotnie większej od rezystancji charakterystycznej tego obwodu.

Te wnioski są może dla Ciebie zaskoczeniem, ale naprawdę nie ma w tym nic z magii − w sumie jest to nawet bardzo proste. Okazuje się tylko, że dla pełnego zrozumienia problemu trzeba bliżej zapoznać się z pojęciem oporności. Zróbmy to w tym odcinku.

Ten odcinek jest nieco trudniejszy niż materiał, który przedstawiłem wcześniej, dlatego nie przejmuj się, jeśli wszystkiego nie zrozumiesz od razu. Być może podane wiadomości będziesz stopniowo układał sobie w głowie, wracając kilkakrotnie do tego artykułu. Jeśli jednak chcesz zajmować się elektroniką na poważnie, to wiedz, że podane tu wnioski są dla Ciebie bardzo istotne i przydadzą Ci się wielokrotnie w przyszłości.

Zadaj więc sobie trochę trudu i spróbuj nadążyć za podanym tokiem rozumowania.

Dodawanie reaktancji

Do tej pory ogólnie mówiliśmy o różnych rodzajach oporności. Znasz już pojęcie rezystancji − występuje ona przy prądzie stałym i zmiennym. Wyraża się ją w omach.

Wiesz także, że dla prądu zmiennego cewka i kondensator przedstawiają sobą pewien opór (reaktancję indukcyjną i pojemnościową). Reaktancję tę także wyrażamy w omach. Ale chyba czegoś jeszcze o tych omach (a właściwie o tych opornościach) nie wiemy…

Połącz w szereg dwa rezystory 100-omowe. Oporność wypadkowa będzie oczywiście sumą obu oporności składowych − wyniesie ona 200 Ω. Ale gdy w szeregowym obwodzie rezonansowym dodają się dwie idealne reaktancje (pojemnościowa i indukcyjna), obie mające po 100 Ω, to oporność wypadkowa wyniesie 0 Ω (spójrz na rysunek 7 w poprzedniej części).

Czyżby więc istniały trzy rodzaje omów? Omy rezystancyjne, omy indukcyjne i omy pojemnościowe? Jak to jest, że jeśli dodajemy „omy rezystancyjne”, to wypadkowa oporność się zwiększa, a gdy dodajemy „omy indukcyjne” i „omy pojemnościowe”, wtedy wypadkowa oporność się zmniejsza?

Zauważ, że w obwodzie rezonansowym szeregowym przy częstotliwości rezonansowej liczbowo równe reaktancje cewki i kondensatora zamiast się wprost dodać − zniosły się do zera… A może właśnie się dodały? No, no…

Tak jest! One się dodały i zniosły! Ale czy potrafisz to sobie jakoś wytłumaczyć? Spróbuj ruszyć głową.

Wygląda na to, że reaktancja indukcyjna i pojemnościowa… mają przeciwne znaki. Ale co to mogłoby znaczyć, że kondensator ma jakąś ujemną reaktancję? Nie mów tylko, że to jest bez sensu! Ma to głębokie i praktyczne znaczenie − wierz mi: to Twoja intuicja na razie nie podsuwa Ci żadnego jasnego wytłumaczenia.

Wróć do rysunku 7 w poprzedniej części. Przy połączeniu szeregowym, równe co do wartości liczbowej reaktancje kondensatora i cewki zniosły się do zera. A przy połączeniu równoległym?

Dodały się, to niewłaściwe słowo. One też jakby się zniosły, tylko w efekcie wypadkowa oporność gwałtownie wzrosła (w obwodzie idealnym wzrosłaby do nieskończoności). Trudno to w pierwszej chwili pojąć, ale naprawdę nie ma tu nic z magii. Po prostu czegoś jeszcze o opornościach nie wiemy. Czujemy na razie przez skórę, że oprócz liczbowej wartości reaktancji podawanej w omach, należy tu jeszcze uwzględnić jakiś dodatkowy czynnik, coś w rodzaju znaku plus czy minus. Tą sprawę wyjaśnię Ci za chwilę. Podany tam materiał wprowadzi Cię (mam nadzieję bezboleśnie) w świat profesjonalnej elektroniki, gdzie wykorzystuje się obliczenia na liczbach zespolonych. Nie bój się, to wcale nie jest trudne.

Na razie wracamy do naszego obwodu rezonansowego.

Zależności fazowe − impedancja

Wróćmy jeszcze raz do podstawowego obwodu rezonansowego, który pokazałem Ci na rysunku 1. Czy zgodzisz się ze stwierdzeniem, że prąd płynący przez cewkę i kondensator, to ten sam prąd? Czy można powiedzieć, że napięcia na cewce i kondensatorze mają taką samą wartość? Nie protestujesz?

Zastanówmy się nad tym dokładniej.

Przy analizie obwodów elektrycznych, musimy zachować jakiś porządek i pewne reguły, w przeciwnym wypadku zginiemy marnie przy próbie analizy bardziej skomplikowanego układu. Aby nie pogubić się w obliczeniach, zaznaczamy kierunki przepływu prądu i kierunek napięcia. Takie zaznaczanie nazywa się strzałkowaniem.

W obwodach prądu stałego sprawa jest bardzo prosta. W przypadku napięć strzałka wskazuje punkt o wyższym potencjale (bardziej dodatni). Umówiliśmy się, że strzałka wskazuje kierunek prądu od bieguna dodatniego do ujemnego (a właściwie od punktu o wyższym potencjale do punktu o niższym potencjale). Ten umowny kierunek przepływu prądu jest przeciwny, niż ruch nośników prądu − elektronów, ale to akurat nie ma żadnego znaczenia.

Jeśli pamiętasz ze szkoły prawo Kirchoffa dla napięć, to niniejsze rozważania tym bardziej będą dla Ciebie jasne. Twierdzenie to mówi, że w każdym obwodzie zamkniętym, suma napięć na elementach tworzących obwód jest w każdej chwili równa zeru.

Jeśli nie jest to dla Ciebie do końca jasne, popatrz na rysunek 2. W tym prostym obwodzie zamkniętym (tak zwanym oczku) oznaczyłem, czyli zastrzałkowałem, występujące tam napięcia. Wybrałem też kierunek obiegu tego oczka (może to być kierunek zgodny z ruchem wskazówek zegara albo przeciwny − nie ma to znaczenia). Napięcia zastrzałkowane zgodnie z kierunkiem obiegu oczka biorę ze znakiem plus, zastrzałkowane przeciwnie − ze znakiem minus.

Zgodnie z napięciowym prawem Kirchhoffa otrzymuję:

UB + (−UR) + (−UD) = 0

czyli:

UB − UR − UD = 0

Taki zapis może się wydać dziwny i niepotrzebny. Ale przecież po przeniesieniu UR i UD na drugą stronę znaku równości, otrzymujemy równanie, którego sens jest oczywisty:

UB = UR + UD

W tak prostym układzie można obyć się bez strzałkowania. Ale przy skomplikowanych sieciach strzałkowanie ułatwia życie, a czasami wręcz umożliwia obliczenia.

Czy jednak strzałkowanie ma sens w przypadku przebiegów zmiennych?

To bardzo ważne pytanie! Strzałkowanie ma nam pomagać i musi mieć jakiś sens fizyczny. Przy przebiegach przemiennych, a zwłaszcza sinusoidalnych, nie bardzo możemy mówić o punktach o wyższym, czy niższym potencjale, bo napięcie ciągle się tam zmienia. Możemy jednak mówić o wartościach chwilowych. W takim wypadku strzałkowanie jak najbardziej ma sens. Przy zaznaczaniu wartości chwilowych napięcia i prądy oznaczmy małymi literami u, i, w odróżnieniu od dużych liter w obwodach prądu stałego.

Niestety, operowanie wartościami chwilowymi, a zwłaszcza jakiekolwiek obliczenia tych wartości, są w praktyce bardzo kłopotliwe.

Tu pozwolę sobie na małą dygresję. Na pewno wiesz, że przy przebiegach zmiennych mówi się o wartości maksymalnej, czyli szczytowej, oznaczanej: U_m, U_max, U_p (peak − szczyt), U_A. Jest to tak zwana amplituda przebiegu zmiennego. W praktyce często podaje się wartość międzyszczytową, czyli podwójną wartość amplitudy (oznaczaną U_PP).

Jednak najczęściej używa się pojęcia wartości skutecznej przebiegu zmiennego. Według prostej, ale prawdziwej definicji, wartość skuteczna napięcia zmiennego jest równa wartości napięcia stałego, które na danej rezystancji spowoduje wydzielenie takiej samej ilości ciepła, jak to napięcie zmienne. Podobnie można zdefiniować wartość skuteczną natężenia prądu zmiennego. Dla przebiegu sinusoidalnego wartość skuteczna jest równa 1/√2 wartości szczytowej, czyli w przybliżeniu 0,707. Zapamiętaj wartość liczby √2 (około 1,41) oraz 1/√2 czyli około 0,707. Jeśli znasz wartość skuteczną napięcia (prądu) sinusoidalnego, napięcie szczytowe obliczysz, mnożąc ją przez 1,41. Znając wartość szczytową (amplitudę), mnożąc ją przez 0,707 obliczysz wartość skuteczną. Zapamiętaj to raz na zawsze − jest to bardzo przydatne w praktyce.

A teraz wracamy do głównego wątku. Jeśli obierzemy kierunek obiegu oczka i zaznaczymy napięcia chwilowe na cewce i kondensatorze obwodu rezonansowego, to zgodnie z napięciowym prawem Kirchhoffa, suma napięć (chwilowych) w oczku musi być równa zeru. Napięcia na cewce i kondensatorze w każdej chwili będą mieć tę samą wartość, ale przeciwne… kierunki.

Może ostro zaprotestujesz: na dwóch połączonych równolegle elementach zawsze występuje to samo napięcie. I tak, i nie. W sumie jest to kwestia umowy − ale jak wspomniałem, przyjęcie pewnych spójnych zasad oznaczania napięć i prądów znakomicie ułatwia analizę wszelkich, nawet bardzo skomplikowanych układów.

Strzałkowanie napięć i rozwiązywanie układów równań z wieloma niewiadomymi bardzo rzadko stosujemy w naszej elektronicznej praktyce. Wspomniałem tu o napięciowym prawie Kirchhoffa, żeby uzasadnić Ci, dlaczego możemy powiedzieć, że w obwodzie rezonansowym napięcia mają przeciwne kierunki, czyli w każdej chwili suma napięć na cewce i kondensatorze jest równa zeru. Ale co to znaczy różne kierunki?

Spójrz na rysunek 3 − porównaj napięcia chwilowe na kondensatorze i cewce. Widzisz, że napięcia na cewce i kondensatorze mają taką samą wartość, ale niejako przeciwne kierunki. Jak to nazwać i zapisać? Aż prosiłoby się powiedzieć, że napięcie na cewce jest przeciwne, niż na kondensatorze i zapisać je ze znakiem minus. Ale przecież mamy tu do czynienia z napięciami zmiennymi, a nie stałymi, więc chyba nie możemy tu użyć znaku minus? Jak myślisz?

Rzeczywiście, użycie znaku minus mogłoby spowodować zamieszanie i wprowadzić w błąd. Ale jakoś trzeba określić, że napięcia na cewce i kondensatorze są w jakiś sposób przeciwne.

Ale nie koniec na tym. Spojrzyj na rysunek 4. Rysunek 3 rozbiłem na trzy części. Na rysunku 4a znajdziesz przebiegi dotyczące kondensatora, a na rysunku 4b − cewki. Rysunki te dotyczą nie tylko obwodu rezonansowego, ale każdego obwodu napięcia zmiennego, zawierającego źródło napięcia sinusoidalnego i „czystą” pojemność lub indukcyjność. Dlatego na rysunku 4 narysowałem dodatkowo takie obwody. Natomiast rysunek 4c pokazuję Ci jeszcze obwód zawierający źródło napięcia zmiennego i rezystor oraz przebieg napięcia i prądu w tym obwodzie w pewnym odcinku czasu.

Przebiegi z rysunku 4 pokazują fundamentalne zależności między prądem a napięciem w obwodach prądu zmiennego.

Przed chwilą zastanawialiśmy się, jak zapisać fakt, że napięcia zmienne na cewce i kondensatorze są niejako przeciwne − teraz mamy dalszy problem: jak zapisać, że przebiegi napięcia na wspomnianych rysunkach są przesunięte względem prądu. We wszystkich trzech przypadkach do elementów przyłożyliśmy takie same napięcie zmienne. Zmierzona amperomierzem wartość prądu jest we wszystkich przypadkach taka sama. Znaczy to, że oporność pokazanych elementów, wyrażona w omach, jest jednakowa.

Zauważ, że w obwodzie z rezystorem pokazanym na rysunku 4c nie ma przesunięcia. W obwodzie z kondensatorem wygląda na to, że zmiany prądu wyprzedzają zmiany napięcia (co wcale nie znaczy, że kondensator jest elementem „przewidującym”, który wcześniej przewiduje zmiany napięcia) − inaczej mówiąc, przebieg napięcia na kondensatorze opóźnia się względem prądu. Przy cewce, zmiany prądu opóźniają się względem zmian napięcia.

Jak to opisać i nazwać? Oprócz oporności wyrażonej w omach trzeba wprowadzić miarę tego przesunięcia. Może się zdziwisz, jeśli powiem, że bardzo wygodną miarą tego przesunięcia wcale nie jest czas (na co mogłyby wskazywać dotychczasowe rysunki), tylko kąt.

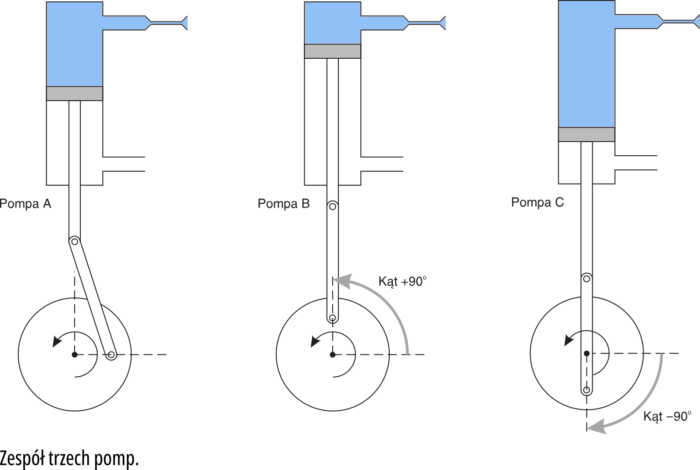
Dlaczego kąt? Nieprzypadkowo rysowałem Ci wcześniej pompę tłokową wraz z kołem napędzającym. Popatrz na trzy pompy pokazane na rysunku 5. Nie jest to rysunek jednej pompy w trzech różnych chwilach czasowych. Jest to zespół trzech pomp, które są napędzane wspólnym silnikiem; czyli prędkość i częstotliwość drgań będą takie same. Jeden cykl pracy pompy to jeden obrót koła napędzającego, czyli obrót o kąt 360°.

Niech Cię to nie dziwi − przebieg sinusoidalny i funkcja sinus mają ścisły związek z kołem. Zgadza się to z praktyką: przecież sinusoidalny przebieg napięcia sieci energetycznej też jest wytwarzany przez wirujące generatory.

Czym różnić się będą przebiegi ciśnienia wytwarzanego przez te trzy pompy?

Oczywiście przebiegi te będą wzajemnie przesunięte. Spójrz na rysunek 6. Bardzo przypomina nam to przebiegi z rysunków 3 i 4. Na rysunkach 5 a, b i c zaznaczyłem kąty. Wiesz chyba ze szkoły, że kierunek przeciwny do ruchu wskazówek zegara przyjęto nazywać kierunkiem ujemnym. Stąd kąt +90° i −90°. Zauważ, że możemy zmieniać prędkość wirowania, czyli częstotliwość przebiegów, ale zależności między tymi trzema przebiegami, pokazane na rysunku 6, zawsze pozostaną stałe. Tu widzisz, dlaczego czas nie jest dogodną miarą przesunięcia − czas zmienia się wraz z częstotliwością, a kąt w tym wypadku nie.

Mamy więc brakującą wielkość, charakteryzującą przebiegi zmienne: jest to pewien kąt − w elektronice kąt ten nazywamy fazą.

Teraz chyba nie zaprotestujesz, jeśli powiem, że przebieg pompy B wyprzedza przebieg pompy A o 90 stopni, a przebieg pompy C opóźnia się w stosunku do przebiegu pompy A o 90 stopni. Przebieg z pompy B wyprzedza przy tym przebieg pompy C o 180 stopni.

Wprowadziliśmy właśnie pojęcie fazy. Przebieg sinusoidalny możemy w pełni scharakteryzować podając jego amplitudę (lub wartość skuteczną) oraz fazę w stosunku do innych przebiegów.

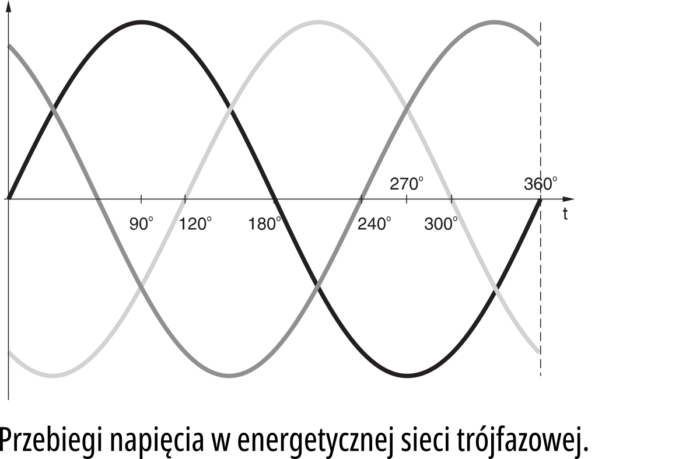
Na przykład w sieci energetycznej mamy prąd trójfazowy − przebiegi napięcia w kolejnych fazach są przesunięte o kąt 120° (360° : 3) zaprezentowane jest to na rysunku 7.

Wracaj teraz do rysunków 3 i 4. Teraz już powinieneś rozumieć, dlaczego mówimy, że w kondensatorze prąd wyprzedza napięcie o 90 stopni, a w cewce prąd opóźnia się względem napięcia o 90 stopni.

A teraz bardzo uważaj! Przechodzimy do bardzo ważnego zagadnienia! Skąd się bierze to opóźnianie i wyprzedzanie?

Pomyśl samodzielnie. W obwodzie prądu zmiennego z rezystorem nie ma przesunięcia…

Do tej pory mówiliśmy o rezystancji, reaktancji indukcyjnej i pojemnościowej jako o opornościach wyrażanych w omach. Umiemy obliczyć ich wartość liczbową. Wartość liczbowa rezystancji, jednej i drugiej reaktancji może być taka sama, ale coś przecież je różni…

Nie masz chyba wątpliwości, że przesunięcia prądu i napięcia są skutkiem, a przyczyna tkwi we właściwościach oporności, ściślej − reaktancji. Rezystancja nie przesuwa fazy prądu względem napięcia. Każda z reaktancji przesuwa fazę o 90° − jedna o +90 stopni, druga o −90 stopni.

Czy po naszych dotychczasowych rozważaniach nie masz wrażenia, że „om, omowi nierówny” i że poszczególne oporności trzeba potraktować jako różne odmiany jakiejś ogólnej oporności?

Czy w przypadku oporności również nie powinniśmy wykorzystać pojęcia fazy, czyli kąta przesunięcia? Wszystko wskazuje, że tak.

Jeszcze raz przeanalizuj sprawę i upewnij się, że przesunięcia prądu względem napięcia, pokazane na kilku wcześniejszych rysunkach wynikają ni mniej ni więcej, tylko właśnie z jakiś dziwnych właściwości oporności (ściślej mówiąc reaktancji pojemnościowej i indukcyjnej).

To nam w dużym stopniu wyjaśnia, dlaczego przy szeregowym i równoległym połączeniu reaktancji otrzymaliśmy takie dziwne wyniki − po tworząc rysunek 6 w poprzedniej części i sumując reaktancje nie uwzględniliśmy zależności fazowych, czyli kątowych. To nam też pomaga zrozumieć, dlaczego mieliśmy wrażenie, że reaktancje pojemnościowa i indukcyjna są niejako odwrotne − coś w tym jest, różnica fazy wynosi 180 stopni.

Czy już do Ciebie dotarło, że rezystancja i obie reaktancje są szczególnymi przypadkami jakiejś ogólnej oporności? Jeśli dotarło, to zrozumiałeś pojęcie impedancji.

Impedancja jest opornością ogólną, fachowo mówiąc − zespoloną. Impedancja może zmieniać się z częstotliwością. Impedancję oznaczamy literą Z, a na schematach zastępczych rysowana jest w postaci takiej jak inne oporności − patrz rysunek 8.

Można powiedzieć, że rezystancja, reaktancja pojemnościowa i indukcyjna są szczególnymi przypadkami impedancji. Na przykład impedancja idealnego kondensatora jest w rzeczywistości „czystą” reaktancją.

Tak samo szczególnym przypadkiem jest impedancja dla prądu stałego − częstotliwość jest wtedy równa zeru, a więc reaktancja pojemnościowa ma wartość nieskończenie wielką, a indukcyjna − równą zeru. Dlatego w obwodzie prądu stałego interesują nas tylko rezystancje.

W ogólnym przypadku impedancja nie musi być „czystą” reaktancją lub „czystą” rezystancją. Może niejako składać się z rezystancji, oraz z reaktancji. Na rysunku 9 znajdziesz kilka tak zwanych dwójników − dwuzaciskowych sieci składających się z różnych elementów. Popatrz uważnie na ten rysunek. Znajdziesz tam między innymi schemat zastępczy rzeczywistej cewki (10b) oraz nasze obwody rezonansowe. Nie masz chyba wątpliwości, że każdy z pokazanych dwójników ma jakąś impedancję. Niewątpliwie we wszystkich przypadkach impedancja ta zależy od częstotliwości.

Chyba Cię trochę zasmuciłem. Zrozumiałeś, że przy obliczeniach impedancji, czyli oporności złożonej z rezystancji i reaktancji, oprócz wartości liczbowej wyrażanej w omach musisz uwzględnić kąt. Na razie jeszcze nie potrafisz przeprowadzać takich obliczeń. Nie martw się − zajmiemy się tym już niedługo. Ale jak by nie było, jeśli nadążasz za mną i zrozumiałeś wszystko, co przedstawiłem Ci do tej chwili, uczyniłeś bardzo duży i ważny krok w kierunku profesjonalnej elektroniki. Poczułeś problem impedancji. Jesteś o krok od wykorzystania liczb zespolonych.

Piotr Górecki