Sondy oscyloskopowe – dlaczego są niezbędne?
Artykuł przedstawia najważniejsze, fundamentalne informacje i wyjaśnia, dlaczego podczas pomiarów powszechnie wykorzystywane są sondy tłumiące 10:1 oraz 100:1, a nie sondy 1:1 czy zwykłe kawałki kabla.
To tylko elementarz i uproszczone podejście – dalsze wyjaśnienia podane są w następnym artykule.
Cieszymy się, że z upływem czasu oscyloskopy cyfrowe są coraz tańsze i mają coraz szersze pasmo. Wydaje się, że są to wręcz idealne przyrządy z uwagi na cyfrowe przetwarzanie, kursory, cyfrowe wyniki pomiarów napięć, częstotliwości i czasu. Niestety, dość często uzyskiwane wyniki pomiarów są niewiarygodne. Bardzo niewiarygodne.
Niewiarygodne są przede wszystkim wtedy, gdy dołączenie oscyloskopu zmienia sytuację w badanym układzie. Owszem, oscyloskop pokazuje przebiegi jak najbardziej prawdziwe, ale występujące w układzie po dołączeniu tam oscyloskopu, a nie pokazuje przebiegów występujących podczas normalnej pracy tego układu.
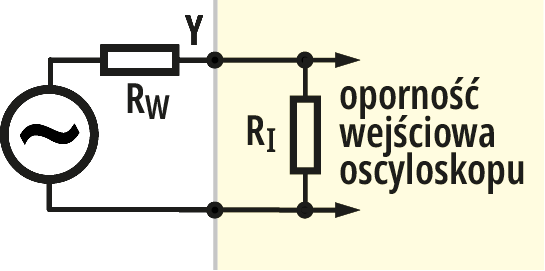
Wszystko zależy od tego, na ile dołączenie oscyloskopu zmienia sytuację w układzie. Można to zilustrować bardzo uproszczonym przykładem, pokazanym na rysunku 1. Badany obwód zawsze ma jakąś, mniejszą lub większą, oporność wewnętrzną RW. A oscyloskop ma jakąś oporność wejściową RI. Nie ulega wątpliwości, że dołączenie oscyloskopu tworzy dzielnik napięcia. Oscyloskop pokazuje napięcie z takiego dzielnika, które zawsze jest mniejsze, niż napięcie w punkcie Y występujące tam podczas normalnej pracy układu, bez dodatkowego obciążenia opornością wejściową RI oscyloskopu.
Najogólniej biorąc, wypadkowa oporność wejściowa RI oscyloskopu powinna być dużo, a wręcz wielokrotnie większa, niż oporność wewnętrzna badanego układu czy obwodu. Wtedy błąd będzie znikomy.
Wiadomo że ogólnie biorąc, oscyloskopy nie mają wysokiej dokładności. Nawet te cyfrowe, na pozór bardzo dokładne. Błąd pomiaru amplitudy zwykle wynosi 2…4%. A to prowadzi do wniosku, że aby nie pogorszyć dokładności pomiaru, oporność wejściowa oscyloskopu powinna być kilkadziesiąt razy, najlepiej co najmniej 100 razy większa od wypadkowej oporności wewnętrznej RW badanego obwodu.
Początkującym wydaje się, że problemu nie ma, bo przecież wejścia prawie wszystkich oscyloskopów mają dużą rezystancję wejściową, równą 1 MΩ.
Tak, rezystancja wejściowa z reguły wynosi 1 megaom, ale tylko rezystancja. A jaka jest impedancja, czyli oporność dla przebiegów zmiennych?
Przecież każdy oscyloskop, oprócz rzeczywiście dość dużej rezystancji, ma też jakąś pojemność wejściową – w lepszych oscyloskopach nieco ponad 10 pF, w gorszych nawet ponad 25 pF.
Przykładowo nadal dość popularny 100-megahercowy Rigol DS1102E ma nominalną pojemność wejściową około 18 pF, jak pokazuje rysunek 2 (niektóre specyfikacje podają 15 pF). Przy tolerancji ±3 pF jego wejście może więc mieć okrągłe 20 pikofaradów. Podobną pojemność mają inne popularne oscyloskopy.
Wydaje się, że te 20 pF to niewiele. Na pozór niewiele, ale… jaka jest reaktancja, a tym samym impedancja przy częstotliwości 100 MHz?
Ze wzoru XC = 1 / (2πfC) łatwo obliczyć, że dla pojemności 20 pF przy 1 kHz jej reaktancja wyniesie 8 MΩ, a przy 10 kHz wyniesie 800 kΩ. Przy dalszym wzroście częstotliwości będzie maleć i przy 1 MHz wyniesie 8 kΩ, a przy 100 MHz tylko 80 omów!
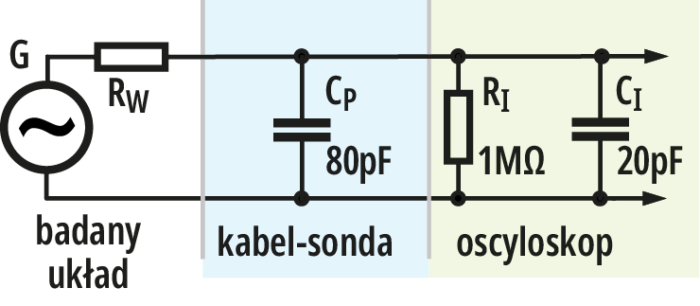
Tak! W tym 100-megahercowym oscyloskopie przy górnej częstotliwości granicznej 100 MHz impedancja wejściowa wynosi tylko 80 Ω! To nie wszystko: jeżeli dołączymy do wejścia oscyloskopu kabel w roli sondy, to do pojemności wejściowej oscyloskopu dojdzie pojemność kabla według rysunku 3.
W pierwszym przybliżeniu możemy przyjąć, że metr kabla ma pojemność około 80…100 pF, zależnie od rodzaju tego kabla. Równolegle do rezystancji wejściowej oscyloskopu RI = 1 MΩ, dołączona będzie więc pojemność co najmniej 100 pF. A pojemność 100 pF już przy częstotliwości 1 MHz będzie mieć reaktancję 1,6 kilooma, a przy 100 MHz tylko 16 omów! A przy górnej częstotliwości 250-megahercowego DHO924 mniej niż 7 omów!
Wygląda na to, że impedancja oscyloskopu z taką sondą przy wysokich częstotliwościach będzie czystą reaktancją pojemnościową o znikomej wartości, a o rezystancji RI = 1 MΩ można wtedy zapomnieć.
Pierwszym problemem jest fałszowanie wyników pomiaru przez stworzenie dzielnika zasygnalizowanego na rysunku 1, ponieważ oprócz rzeczywiście dużej rezystancji RI przy wysokich częstotliwościach mamy też zaskakująco, żałośnie małą reaktancję pojemnościową XC.
Drugi problem to fakt, że podczas takiego pomiaru, do badanego obwodu dołączamy stosunkowo dużą sumaryczną pojemność kabla i oscyloskopu. Jak to wpłynie na działanie tego obwodu?
Jeżeli jest to na przykład obwód zasilania, to dołączenie pojemności 100 pF nie ma żadnego znaczenia. Ale jeżeli będzie to na przykład obwód generatora z rezonatorem kwarcowym albo obwodem LC, to dołączenie pojemności 100 pF na pewno zakłóci jego działanie, a w wielu przypadkach wręcz uniemożliwi prawidłową pracę. Nawet jeśli oscyloskop coś zmierzy, nie będą to przebiegi występujące tam podczas normalnej pracy.
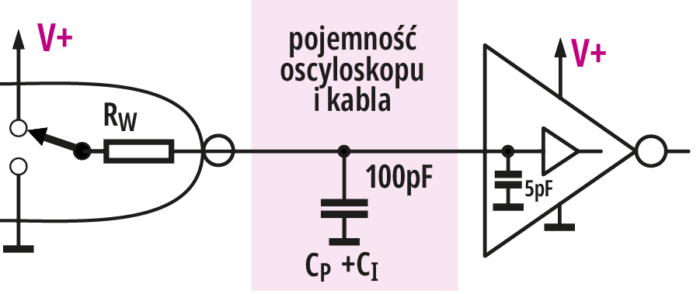
Coraz rzadziej badamy delikatne układy analogowe, coraz częściej cyfrowe, gdzie występują dość silne impulsy o dużej częstotliwości. Wtedy też może powstać poważny problem, ponieważ zgodnie z uproszczonym rysunkiem 4 dołączenie pojemności kabla + oscyloskopu 100 pF dodaje się do pojemności tam istniejących i zwiększa stałą RC, a to znacząco opóźnia sygnał cyfrowy, zależnie od wartości rezystancji wyjściowej RW (i wydajności prądowej źródła impulsów). Dołączenie kabla oscyloskopu w istotny sposób zmienia sytuację w układzie i może spowodować błędy w działaniu po dołączeniu oscyloskopu. A w najlepszym przypadku wystąpią znaczące błędy pomiaru czasów i opóźnień w porównaniu z tymi, które tam występują podczas normalnej pracy.
Takie pomiary mogą okazać się nie tylko bezwartościowe, ale wręcz wprowadzić w błąd!
(…)
——– ciach! ——–
To jest tylko fragment artykułu, którego pełna wersja ukazała się w numerze lipcowym czasopisma Zrozumieć Elektronikę (ZE 7/2024). Czasopismo aktualnie nie ma wersji drukowanej na papierze. Wydawane jest w postaci elektronicznej (plików PDF). Pełną wersję czasopisma znajdziesz na moim profilu Patronite i dostępna jest dla Patronów, którzy wspierają mnie kwotą co najmniej 10 zł miesięcznie. Natomiast niepełna, okrojona wersja, pozwalająca zapoznać się z zawartością numeru ZE 7/2024 znajduje się tutaj.
Piotr Górecki
Uwaga! Wskazówki, jak nabyć archiwalne numery znajdują się na stronie: https://piotr-gorecki.pl/n11
Chodzi o ZE 7/2024.